想象两个世界,它们有两个不同的概率分布。其中一个概率分布 p 描述了事物的真实模式,也就是每个事件实际发生的频率。另一个概率分布 q 是你的信念或是模型认为的,这些相同事件的概率分布情况。
Kullback-Leibler 散度(KL 散度)衡量的是,如果你生活在世界 p 中,但仍然相信 q,你会经历多少额外的"意外"。
如果 q 与 p 完全匹配,那么你看到的每个事件都与预期完全一致,没有额外的意外。但如果 q 是错误的,那么从 p 观察到的每一个事件都会带来惩罚,你的预测总是会有点偏差。
从数学上讲,它表示为:
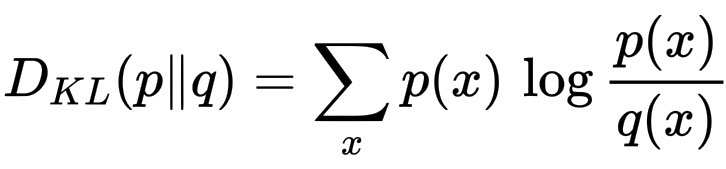
D_{KL}(p\|q) = \sum_x p(x)\,\log \frac{p(x)}{q(x)}。
你也可以将其视为两个熵之间的差:
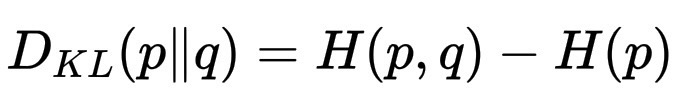
D_{KL}(p\|q) = H(p,q) - H(p),
其中 H(p) 是真实熵(世界真正的不确定性程度),H(p,q) 是交叉熵(如果用 q 代替,你感觉的不确定性程度)。
所以,KL 散度确实是"熵"家族的一部分。如果熵告诉你世界的不确定性程度,交叉熵告诉你你认为世界的不确定性程度,那么 KL 散度告诉你"你的想法"与事实的偏差程度。
这里有一个神奇的事情,KL散度永远是非负的!
实际上,对于所有分布 p、q,D_{KL}(p \| q) = 0,并且只有当 p(x) = q(x) 时,等式才成立。
对数对低估(q(x) < p(x))的惩罚远比对高估(q(x) > p(x))的奖励更严厉!
这完全符合直觉,对数函数是不对称的,所以当 q 的概率质量太小而 p 的概率质量很大时,惩罚的爆发速度比任何小的高估都能弥补的速度要快得多。
这就是为什么,"负"区域无法抵消"正"区域。从数学上讲,正是这种不对称性使得对数比的期望 E_p[\log(p/q)] 始终为非负值。
简短清晰地证明 D_{KL}(p\|q) ≥ 0(吉布斯不等式)。
下面将使用 Jensen 不等式(通过 -\log 的凸性)给出标准的简洁论证,然后说明相等条件。
设 p 和 q 是同一离散空间上的概率分布,KL 散度为
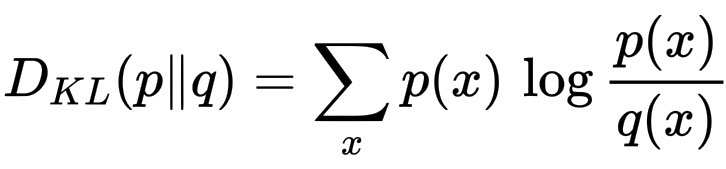
D_{KL}(p\|q)=\sum_x p(x)\,\log\frac{p(x)}{q(x)}。
将其重写为期望:
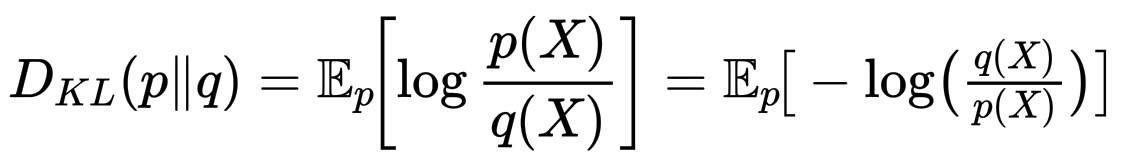
D_{KL}(p\|q)=\mathbb{E}_{p}\!\left[\log\frac{p(X)}{q(X)}\right] = \mathbb{E}_p\!\big[-\log\!\big(\tfrac{q(X)}{p(X)}\big)\big]。
现在将 Jensen 不等式应用于凸函数 f(u)=-\log u。Jensen 表示:
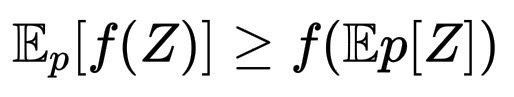
\mathbb{E}_p[f(Z)] \ge f(\mathbb{E}p[Z])
对于任意随机变量 Z,取 Z=\dfrac{q(X)}{p(X)},则
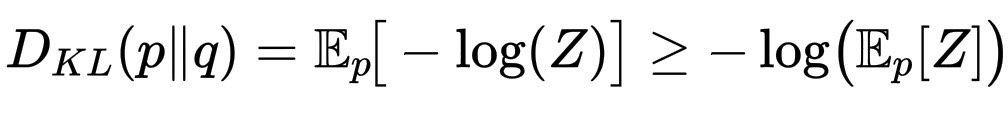
D_{KL}(p\|q) = \mathbb{E}_p\!\big[-\log(Z)\big] \ge -\log\!\big(\mathbb{E}_p[Z]\big)。
计算 \mathbb{E}_p[Z]:
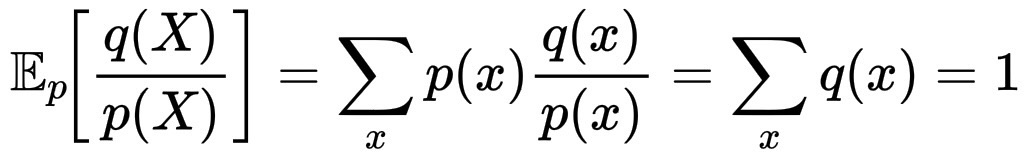
\mathbb{E}_p\!\left[\frac{q(X)}{p(X)}\right] = \sum_x p(x)\frac{q(x)}{p(x)}=\sum_x q(x)=1。
因此
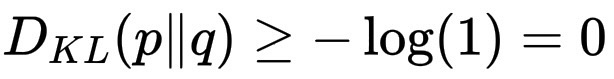
D_{KL}(p\|q) \ge -\log(1)=0。
等式条件:Jensen 不等式是严格的,当且仅当 Z 在 p 下几乎必然为常数,即对于每个满足 p(x)>0 的 x,\frac{q(x)}{p(x)} 相等。因为 p 和 q 都经过归一化处理,所以该常数必定为 1,因此对于所有 p(x)>0 的 x,q(x)=p(x)。因此,D_{KL}(p\|q)=0,当且仅当 p=q(在 p 的支持集上)。
快速推论,因为 D_{KL}(p\|q)=H(p,q)-H(p),D_{KL} 的非负性意味着 H(p,q)≥H(p),也就是说,交叉熵始终大于等于真实熵,而只有当模型与真实分布匹配时,交叉熵才等于真实熵。