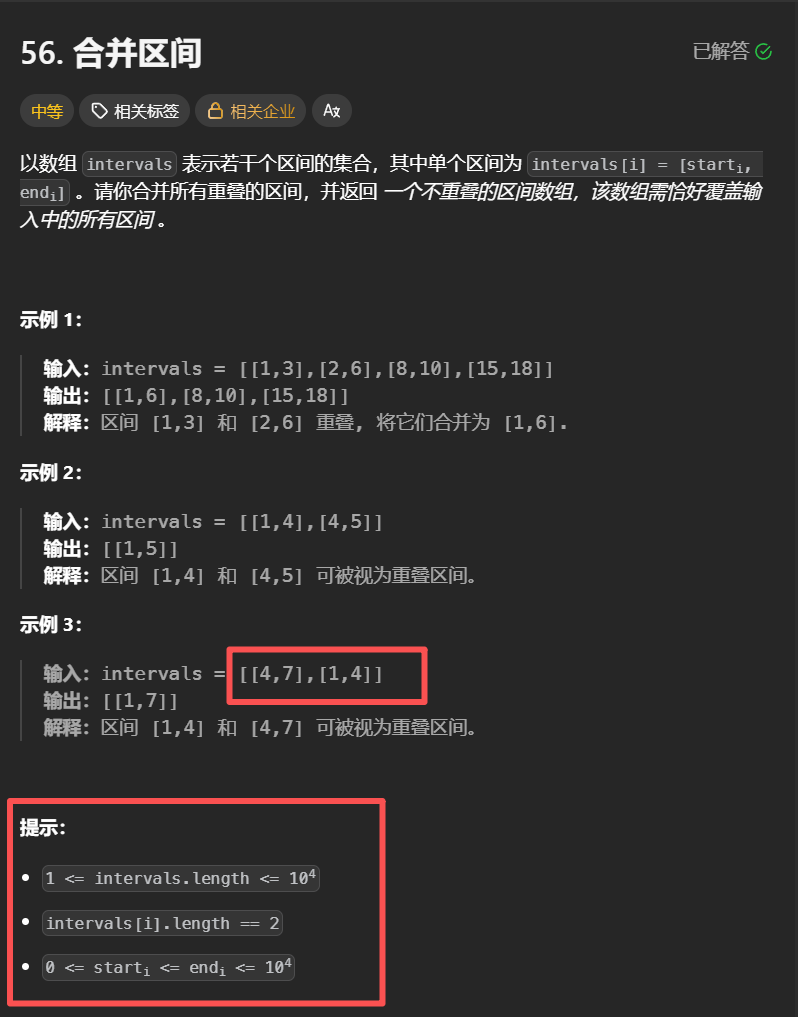
1.题目
核心思路:
这个算法的核心可以总结为两个步骤:"先排序,再合并"。
第一步:排序 (算法的灵魂)
为什么排序这么重要?
想象一下,你拿到一堆乱七八糟的时间安排,比如 [下午3点-5点], [上午9点-10点], [下午4点-6点]。要合并它们,你肯定会下意识地先把它们按开始时间理顺:
-
[上午9点-10点] -
[下午3点-5点] -
[下午4点-6点]
排序之后,事情就变得简单了。你只需要按顺序一个一个地看,而不用回头担心前面会不会有更早的安排。
代码中的 std::sort(...) 就是在做这个整理工作。它确保了我们接下来处理的区间,其起点 永远不会比我们已经合并好的区间的起点更早。
第二步:合并 (核心判断逻辑)
if (current_interval[0] <= last_interval[1])
"当前区间的起点 <= 结果中最后一个区间的终点"
由于我们已经排过序了,我们只需要比较两个区间:
-
last_interval:我们刚刚合并好(或者是第一个)的区间。 -
current_interval:我们正要处理的下一个区间。
因为排过序,我们已经100%确定 current_interval 的起点 不会早于 last_interval 的起点。所以,判断它们是否重叠,只需要考虑一种情况:
current_interval 是不是在 last_interval 结束之前就开始了?
这就是 current_interval[0] <= last_interval[1] 这句判断的直白翻译。
我们来看两个例子:
例1:重叠
-
merged里的最后一个区间last_interval是[1, 6]。 -
我们现在要处理的
current_interval是[2, 8]。
判断 2 <= 6 是否成立? 成立!
这意味着,在 [1, 6] 这个区间还没结束的时候,[2, 8] 这个区间已经开始了。所以它们必然重叠。
last_interval: [1******************6]
current_interval: [2*********************8]
重叠了!例2:不重叠
-
merged里的最后一个区间last_interval是[1, 6]。 -
我们现在要处理的
current_interval是[8, 10]。
判断 8 <= 6 是否成立? 不成立!
这意味着,在 [1, 6] 结束后,中间隔了一段空白,[8, 10] 才开始。所以它们没有重叠。
last_interval: [1******************6]
(这里有空隙)
current_interval: [8**********10]
没重叠!总结:
算法的核心就是通过排序来简化问题。排序后,我们就有了一个非常可靠的先后顺序,使得判断重叠的条件从暴力法中的复杂判断 (a[1] >= b[0] && b[1] >= a[0]),简化为了一个极其简单高效的判断 (current[0] <= last[1])。