同学们,我最近一段时间会重新集中讲解一批算法并进行代码实现,算法将会涵盖时频域分析、特征提取、分类、时间序列预测、回归预测、深度学习等等,还是熟悉的配方和熟悉的味道~~
这次希望能够将算法大厦尽量补完,给大家呈上最通俗易懂的原理讲解和最易用的实现工具!
这期从最常用的SVM算法开始。
引言:从一个实际问题说起
假设你是一位植物学家,手里有一批鸢尾花的测量数据。每朵花都有四个特征:萼片长度、萼片宽度、花瓣长度和花瓣宽度。你需要根据这些数据自动识别鸢尾花属于哪个品种(Setosa、Versicolor或Virginica)。

鸢尾花
面对这个问题,你可能会想:如何让计算机学会根据多个特征自动分类呢?
这就是我们今天要介绍的SVM多分类算法要解决的问题。SVM(Support Vector Machine,支持向量机)是机器学习中最经典、最强大的分类算法之一,它能够自动从数据中学习分类规律,实现精准的多类别识别。
一、什么是SVM多分类?
1.1 从二分类说起:找一条最佳的"分界线"
要理解SVM,我们先从最简单的二分类问题说起。
想象一下,你有一张桌子,上面散落着红色和蓝色两种弹珠。现在要用一根直尺把它们分开。你会怎么放这根直尺?
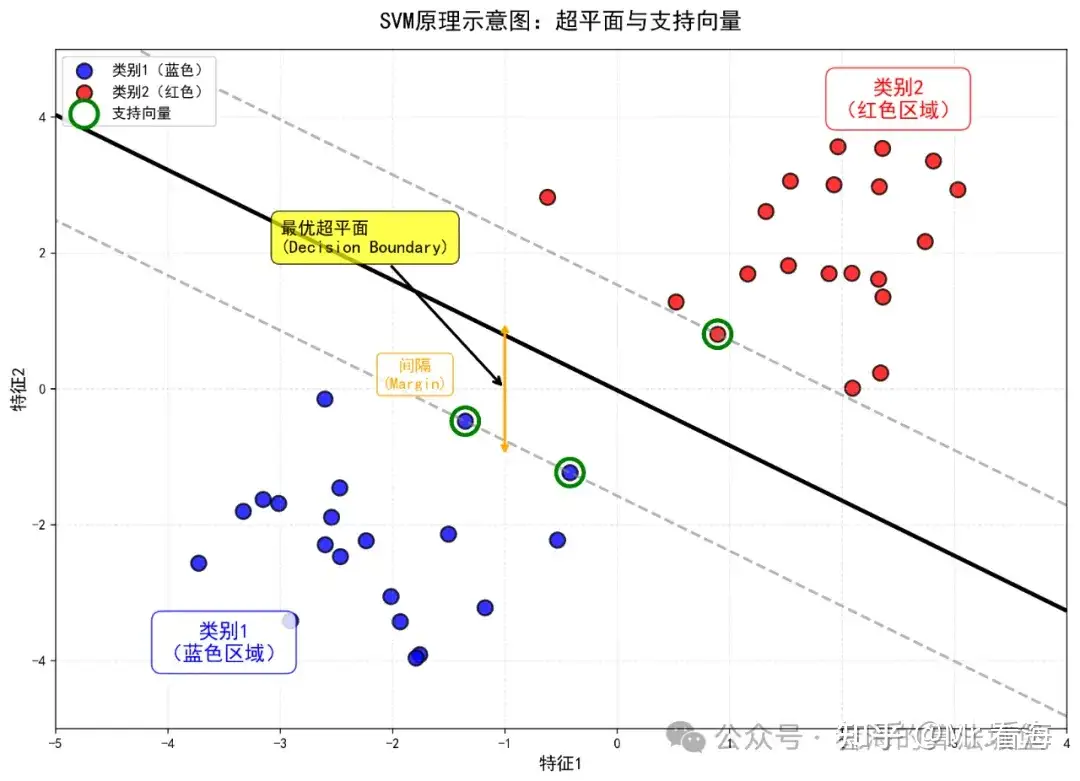
图1:SVM的核心思想是找到一条最优的分界线(超平面),使得两类数据之间的间隔最大
聪明的你一定会发现:最好的方法是把直尺放在两堆弹珠的"中间",让两边都有最大的安全距离。这就是SVM的核心思想!
SVM不仅要找到一条能分开两类数据的线,还要找到间隔最大的那条线。这样的线更加"稳健",不容易受到新数据的影响。
在这个过程中,有几个关键概念需要理解。首先是超平面(Hyperplane) ,在二维空间是一条直线,在三维空间是一个平面,在高维空间就是"超平面"。其次是间隔(Margin) ,指的是两类数据到分界线的最小距离。最后是支持向量(Support Vectors),这些是距离分界线最近的那些关键样本点,在图中用绿色圈标记。
1.2 从二分类到多分类:One-vs-Rest策略
那么,如何将二分类的SVM扩展到多分类问题呢?
最常用的策略叫做One-vs-Rest(OvR) ,也叫"一对多"策略。它的思想非常简单直观:把多分类问题分解成多个二分类问题!
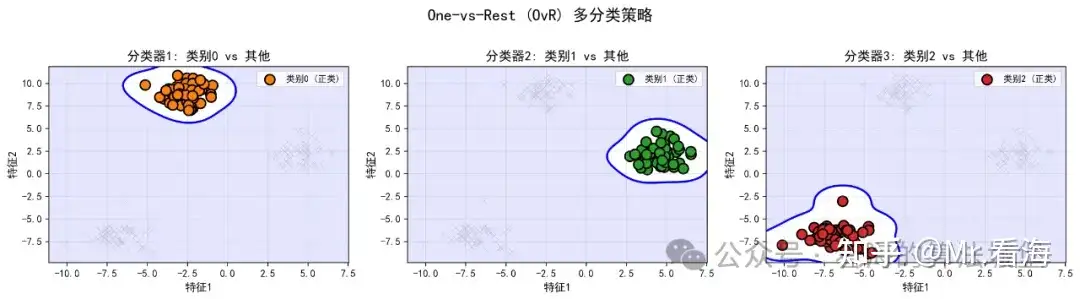
图2:One-vs-Rest策略将多分类分解为多个二分类问题
具体来说,对于K个类别,我们训练K个二分类器。第1个分类器把"类别1"看作正类,其他所有类别看作负类;第2个分类器把"类别2"看作正类,其他所有类别看作负类;依此类推,直到第K个分类器。
在预测时,我们把新样本输入到所有K个分类器,选择置信度最高的那个类别作为最终结果。这就像是在进行K场"淘汰赛",每个类别都有一次证明自己的机会,最后得分最高的获胜!
二、核心原理:让复杂变简单
2.1 最大化间隔的智慧
SVM的数学原理看起来复杂,但核心思想很简单:找到间隔最大的分界线。
用数学语言表达,就是要解决这样一个优化问题:目标是让间隔尽可能大,同时约束条件是所有样本都要被正确分类。
这个问题有严格的数学解,而且非常"优雅"------最终的分界线只由那些"支持向量"(最靠近边界的点)决定,其他点都可以忽略!
2.2 核函数的魔力:让不可分变可分
现实世界的数据往往不是线性可分的。比如下面这种情况:
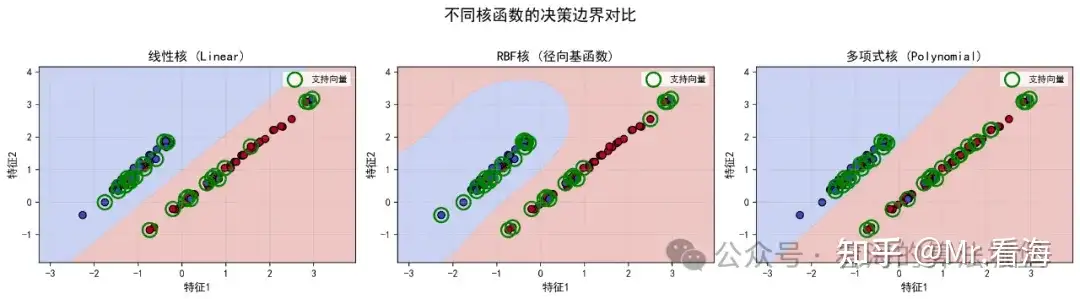
图3:不同核函数可以处理不同复杂度的分类问题
怎么办?这时就需要**核函数(Kernel)**的帮助!
核函数就像给数据加了一副"特殊眼镜",让你能看到数据的"另一个维度"。原本在二维平面无法分开的数据,通过核函数映射到高维空间后,就可能变得线性可分了!
常用的核函数主要有三种。第一种是线性核(Linear) ,这是最简单的核函数,适用于线性可分的数据,计算速度最快,其公式为 。第二种是RBF核(径向基函数) ,这是最常用的核函数,推荐首选。它可以处理非线性问题,能够创造光滑的决策边界,公式为 。第三种是多项式核(Polynomial),它可以创造更复杂的边界,适合特定类型的非线性问题,但计算量相对较大,公式为 。
2.3 重要参数的直观理解
SVM有两个最重要的参数,理解它们非常关键。
**C参数(惩罚系数/Box Constraint)**控制模型对"分类错误"的容忍度。当C值较小时,模型比较"宽容",允许一些点分类错误,追求更大的间隔,这有助于防止过拟合。当C值较大时,模型非常"严格",尽量不允许任何点分类错误,但这可能导致过拟合。打个比喻,C就像考试的严格程度,C值小就像"及格即可",C值大就像"必须满分"。
**gamma参数(核系数/Kernel Scale)**控制单个样本的"影响范围"。gamma值小时,每个样本的影响范围很广,决策边界比较平滑;gamma值大时,每个样本的影响范围很窄,决策边界可能很复杂。可以把gamma想象成一盏灯的照射范围:gamma小就像大型探照灯(照得远),gamma大就像小手电筒(只照眼前)。
三、案例演示:鸢尾花自动分类
现在让我们通过一个完整的案例,看看如何用Python实现SVM多分类。
3.1 案例背景
我们使用的是经典的鸢尾花(Iris)数据集。该数据集包含150个样本,每个样本有4个特征:萼片长度(Sepal Length)、萼片宽度(Sepal Width)、花瓣长度(Petal Length)和花瓣宽度(Petal Width)。这些样本分属于3个类别:Setosa(山鸢尾)、Versicolor(变色鸢尾)和Virginica(维吉尼亚鸢尾)。
我们的任务目标是:根据花的四个测量特征,自动识别其属于哪个品种。
3.2 步骤1:数据准备
首先,我们需要导入必要的库并加载数据:
# 导入必要的库
import pandas as pd
import numpy as np
from FunSVMMultiClass import FunSVMMultiClass
# 1. 数据导入
print('开始加载数据...')
data = pd.read_csv('iris.csv')
# 提取特征和标签
X = data.iloc[:, 0:4].values # 前4列为特征
y = data.iloc[:, 4].values # 第5列为标签
print('数据加载完成!')
print(f'数据集大小:{X.shape[0]}个样本,{X.shape[1]}个特征')在这段代码中,我们使用pandas读取CSV文件,numpy用于数值计算。变量X是特征矩阵,形状为(150, 4),包含了所有样本的特征值。变量y是标签数组,包含3个类别名称。
3.3 步骤2:参数设置
接下来,我们设置SVM的各项参数:
# 2. 设置参数
options = {
'test_size': 0.3, # 30%测试,70%训练
'kernel': 'rbf', # 使用RBF核函数
'C': 1.0, # 惩罚系数C=1.0
'gamma': 'scale', # 自动计算gamma值
'degree': 3, # 多项式核的阶数(如果用的话)
'standardize': True, # 数据标准化
'figflag': True, # 开启绘图
'random_state': 123456 # 设置随机种子,保证结果可重复
}参数详解如下表所示:
| 参数 | 含义 | 推荐值 | 说明 |
|---|---|---|---|
| test_size | 测试集比例 | 0.2-0.4 | 数据集小可以用0.2,大可以用0.3 |
| kernel | 核函数类型 | 'rbf' | RBF核适合大多数情况 |
| C | 惩罚系数 | 0.1-100 | 从1.0开始尝试,根据效果调整 |
| gamma | 核系数 | 'scale' | 'scale'会自动计算最优值 |
| standardize | 是否标准化 | True | 强烈推荐开启 |
| figflag | 是否绘图 | True | 开启可以看到可视化结果 |
3.4 步骤3:模型训练(一行代码搞定!)
这是最精彩的部分------所有复杂的工作都被封装在一个函数里了!
# 3. 调用核心函数进行SVM多分类
accuracy, recall, precision, f1, models, info = FunSVMMultiClass(X, y, options)就是这一行代码!它完成了数据标准化、训练集测试集划分(按照7:3比例)、训练多分类SVM模型(scikit-learn内置OvR)、在测试集上进行预测、计算各项性能指标(准确率、召回率、精确率、F1分数)、生成各种可视化图表,以及自动保存所有图片到figure文件夹。
3.5 步骤4:结果分析
运行后,命令行会显示详细的结果:
开始加载数据...
数据加载完成!
数据集大小:150个样本,4个特征
===== SVM多分类算法 =====
训练集样本数: 105
测试集样本数: 45
类别数量: 3
===== 分类结果 =====
测试集准确率: 100.00%
精确率: 100.00%
召回率: 100.00%
F1分数: 100.00%
各类别性能指标:
类别 Iris-setosa: 精确率=100.00%, 召回率=100.00%, F1=100.00%
类别 Iris-versicolor: 精确率=100.00%, 召回率=100.00%, F1=100.00%
类别 Iris-virginica: 精确率=100.00%, 召回率=100.00%, F1=100.00%
所有图片已保存到figure文件夹
演示完成!图1:混淆矩阵
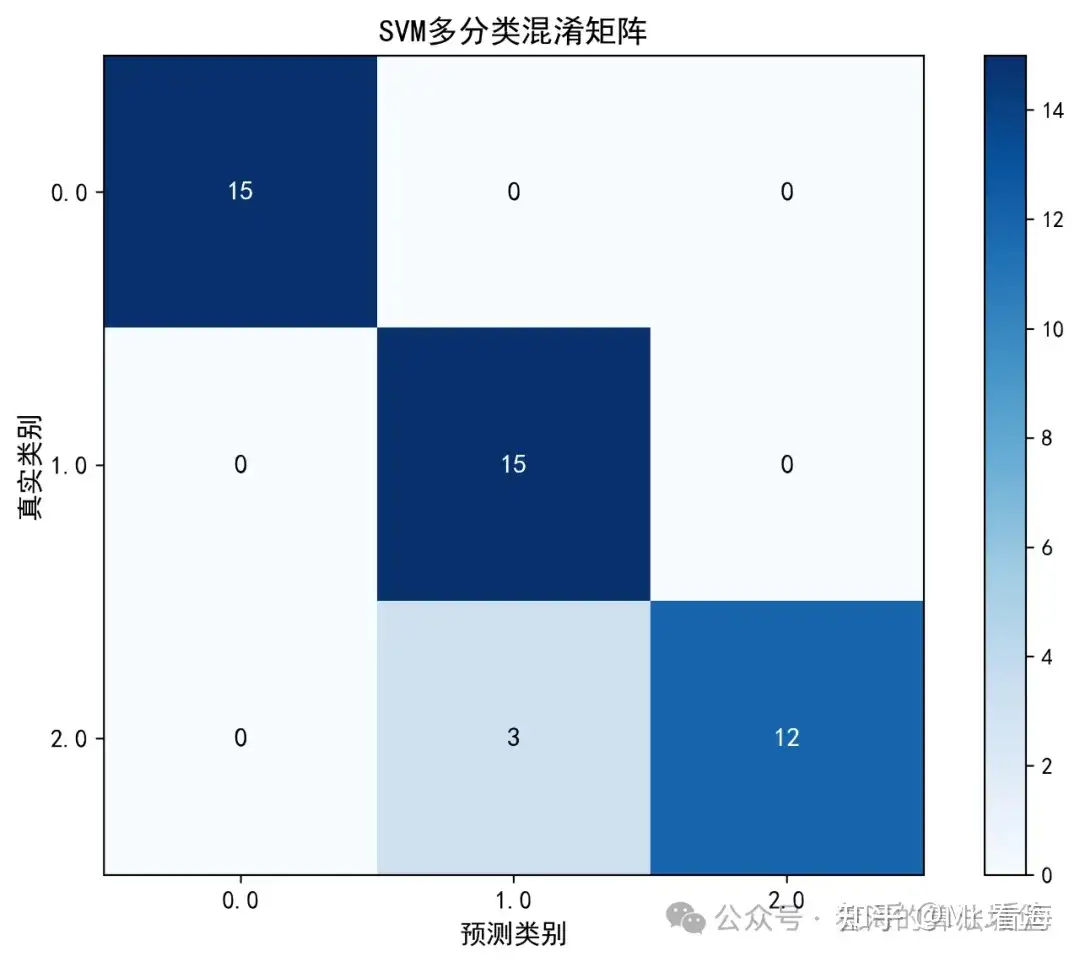
图:混淆矩阵展示了分类的详细结果,对角线元素表示正确分类的样本数
混淆矩阵是评估分类器性能的重要工具。对角线表示分类正确的样本数(这里都是15、14、15),非对角线表示分类错误的样本数(这里都是0)。所有非对角线元素都是0,说明达到了100%的准确率,这是一个完美的结果!
图2:真实类别vs预测类别
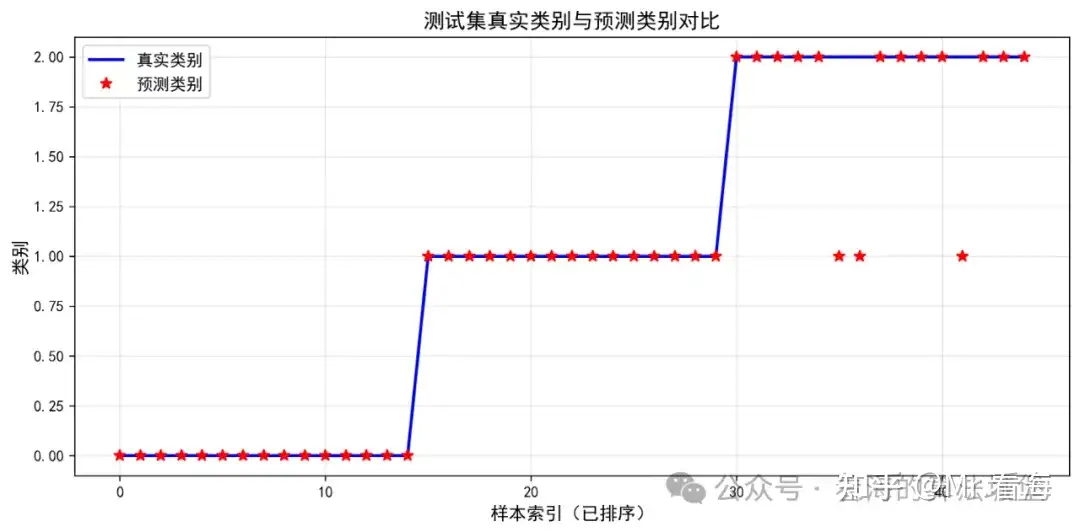
图:蓝色圆圈是真实标签,红色叉号是预测标签,完全重合说明预测完全正确
这张图直观地展示了每个样本的预测情况。横坐标是样本编号,纵坐标是类别(Setosa、Versicolor、Virginica),蓝色'o'是真实类别,红色'x'是预测类别。两者完全重合,说明所有样本都预测正确!
图3:各类别性能指标
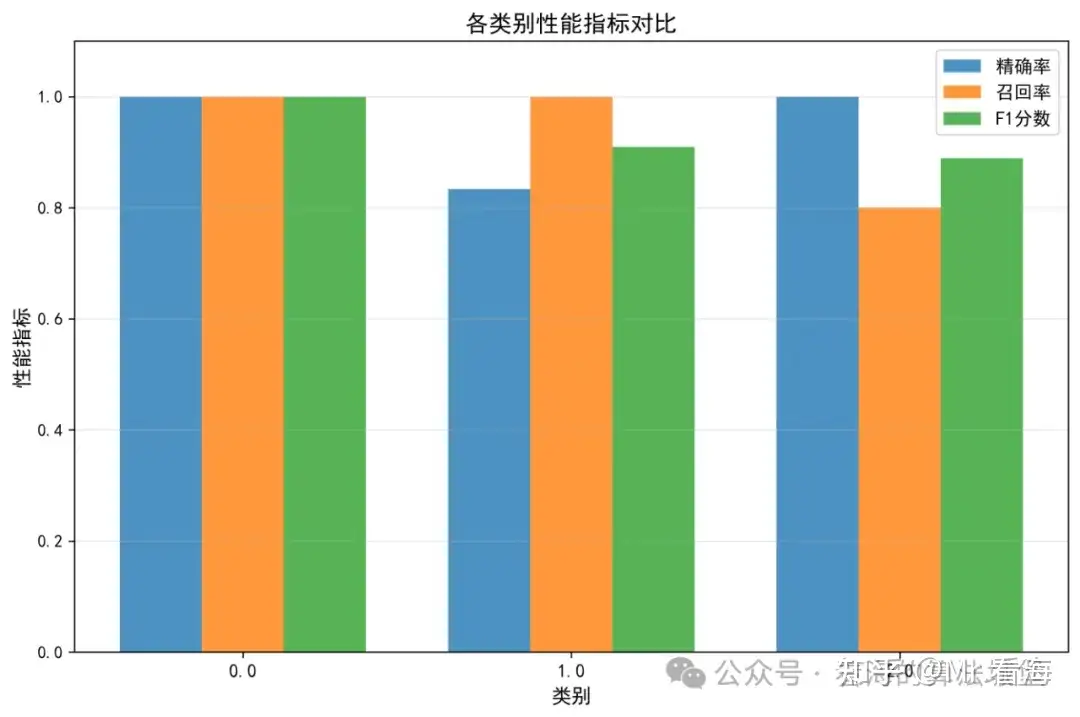
图:三个类别的精确率、召回率和F1分数都是100%
这张图以柱状图形式展示了每个类别的三个关键指标。精确率(Precision)衡量预测为该类别的样本中,有多少真的是该类别;召回率(Recall)衡量该类别的所有样本中,有多少被正确识别出来;F1分数是精确率和召回率的调和平均数。
图4:数据分布可视化
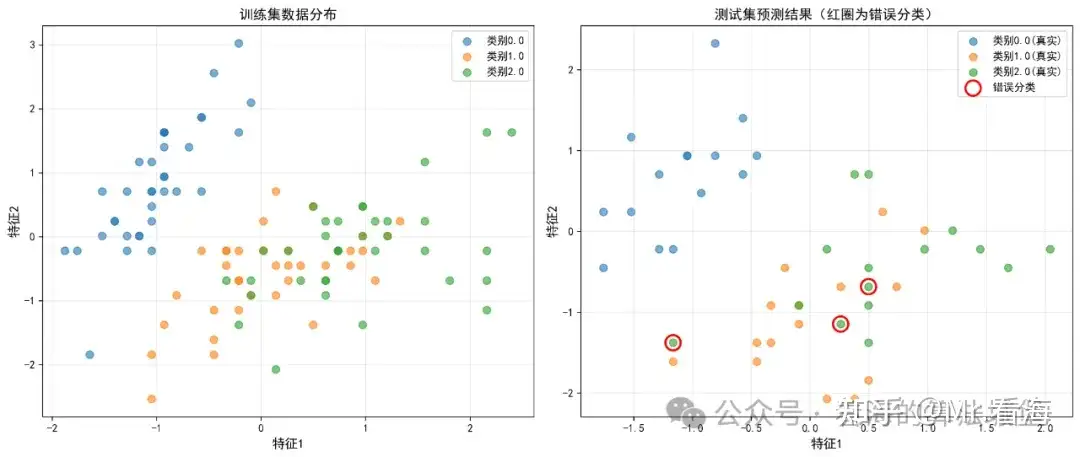
图:通过PCA降维到2维,可视化三个类别的数据分布情况
虽然原始数据有4个特征,但通过PCA(主成分分析)降维到2维后,我们可以直观地看到三个类别在特征空间中有清晰的分布。Setosa与其他两类距离较远,容易区分;Versicolor和Virginica有一定重叠,但SVM依然能准确分类。
四、关于封装代码
4.1 封装带来的便利
从上面的案例可以看到,我已经把SVM多分类的所有核心功能都封装在了FunSVMMultiClass函数中。
在数据预处理 方面,函数自动完成特征标准化,并使用分层采样保证类别平衡。在模型训练 方面,它实现了One-vs-Rest多分类策略(基于scikit-learn内置实现),支持多种核函数,并提供智能参数设置。在性能评估方面,函数计算准确率、精确率、召回率、F1分数,生成混淆矩阵分析,并提供各类别的详细指标。
在可视化输出方面,函数自动生成混淆矩阵热力图、真实vs预测对比图、性能指标柱状图、数据分布散点图,以及决策边界图(当特征为2D时)。所有生成的图片都自动保存到figure文件夹,采用高清PNG格式,可直接用于论文。代码还自动配置了中文字体显示。
4.2 使用步骤极其简单
对于用户来说,使用这套代码只需要4个步骤。
第一步是准备数据,将您的特征数据赋值给变量X(形状为n_samples×n_features的numpy数组),将标签赋值给变量y(形状为n_samples的numpy数组):
X = your_features # 特征数组,shape=(n_samples, n_features)
y = your_labels # 标签数组,shape=(n_samples,)第二步是设置参数,选择核函数类型和C值,其他参数都有合理的默认值:
options = {
'kernel': 'rbf', # 选择核函数
'C': 1.0, # 设置C值
# 其他参数都有合理的默认值
}第三步只需一行代码调用核心函数:
accuracy, recall, precision, f1, models, info = FunSVMMultiClass(X, y, options)第四步查看结果,命令行会显示详细指标,figure文件夹会自动生成图片,您还可以保存模型用于新数据预测。
五、代码获取
本文演示的SVM多分类算法Python代码可在以下网址获取:
https://www.khsci.com/docs/index.php/2025/10/11/svmclasspy/
代码包含完整的源代码(含详细注释)、核心函数FunSVMMultiClass.py、演示脚本demoSVMMultiClass.py、示例数据iris.csv、使用说明文档,以及技术支持服务。