【C++】用红黑树封装map与set

勇闯逆流河2025-10-20 19:40

本文是小编巩固自身而作，如有错误，欢迎指出！

目录

一、封装map和set的底层分析

二、map和set的实现

（1）红黑树的迭代器

1.1迭代器实现思路

1.2迭代器++的实现

1.2.1右子树存在

1.2.2右子树不存在

（2）insert的实现

[（3）map的[ ]插入](#（3）map的[ ]插入)

三、完整代码的实现与测试

RBTree.h

map.h

set.h

test.cpp

测试结果

一、封装map和set的底层分析

想要自己实现map和set，我们首先就要看看他的底层的实现

通过上述代码我们可以发现一个现象是什么呢？

那就是map和set的底层实现共用一个红黑树的模版

那我们之前都学习了解到，map是一个key/value结构的树，set是没有value仅仅有key的树，那么他们为什么能够公用一个模版呢？

原因就是：为了能兼容map，RBTree就多了一个参数Key，来专门存储key

cpp 复制代码 
template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{

	}

};

就像这个节点，其中的T即可以代表set的key也可以代表map的key/value

二、map和set的实现

（1）红黑树的迭代器

1.1迭代器实现思路

红黑树的迭代器其实和list的迭代器很相似，在功能上都很相似，其常规的迭代器就如下。

cpp 复制代码 
struct TreeIterator
{
	typedef	RBTreeNode<T> Node;
	typedef TreeIterator<T, Ref, Ptr> Self;
	Node* _node;

	TreeIterator(Node* node)
		:_node(node)
	{

	}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return  &_node->_data;
	}
bool operator!=(const Self& s)const
	{
		return _node != s._node;
	}
	bool operator==(const Self& s)const
	{
		return _node == s._node;
	}
}；

1.2迭代器++的实现

其主要实现思路其实和list的无二，但主要的难点就在于，在红黑树实现++肯定不能像list一样直接访问next，因此还是需要我们额外进行处理。

list是一种链表结构，访问下一个个节点可以只是指向next，但是红黑树是一种二叉树今结构，所谓的下一个是我们在中序遍历的前提下访问的下一个节点，其并不能直接用next表示。

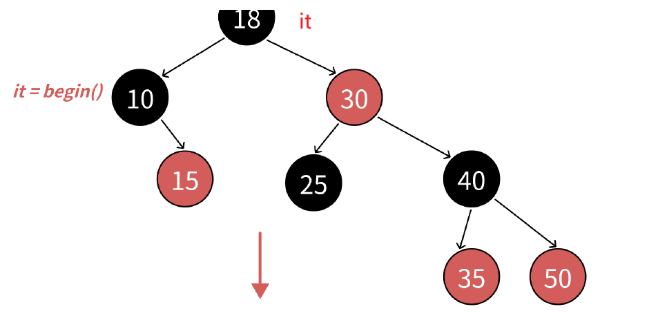
如上图所示，我们可以看到，如果选择在40的地方进行++，很显然下一个就是50，如果在30的地方进行++，下一个就是35，如果在35++，下一个又是40，反而在自己头上了，而在50的地方进行++，我们发现就没有下一个数了，其中以一个重要的判断条件是什么呢？就是进行++的节点的右子树是否存在。

1.2.1右子树存在

当右子树存在的情况下，下一个节点要想做到比自身大而又要比其他的数小要怎么办呢？，要比自身大很简单向右遍历的都比自身大，但是要成为其中最小的，其实也显而易见了，就是最左节点了，因此我们得出一个结论------当右子树存在的时候，++的下一个节点是右子树的最左节点

cpp 复制代码 
//当前右孩子不为空，下一个为柚子树中序最左节点
		if (_node->_right)
		{
			Node* min = _node->_right;
				while(min->_left)
				{
					min = min->_left;
				}
			_node = min;
		}
1.2.2右子树不存在

在右子树不存在的情况下，下一个节点要比自身大，那么明显我们就要向上开始寻找了，而要满足比自己大又比其他的数小，如果自身是左子树，很显然下一个就是parent，，而自身是右子树的情况下，我们就要向上追溯父节点，找到中序的下一个节点

  • 若node是其父节点parent的左孩子 ：根据中序遍历 "左→根→右"，node的左子树已遍历完成，node本身也已访问，接下来自然要访问node的父节点parent（因为parent是 "根"，在左子树node之后访问）。

  • 若node是其父节点parent的右孩子 ：说明parent的左子树和parent本身已经被访问过（因为node作为右孩子，是在parent之后被访问的）。此时parent不能作为下一个节点，需要继续向上追溯parent的父节点（即node的祖父节点），重复判断。

。

cpp 复制代码 
else	// 当前节点右为空，下一个孩子是父亲左的那个祖先节点
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
  • 循环的作用 ：过滤掉所有 "当前节点是其右孩子" 的祖先。因为这些祖先已经被访问过（例如，若node是parent的右孩子，则parent一定在node之前被访问）。
  • 循环终止的两种情况 ：
    1. parent为null：说明node是整个树的最右节点（中序遍历的最后一个节点），没有下一个节点。
    2. cur是parent的左孩子：此时parent就是下一个节点（因为parent作为 "根"，在其左子树cur之后访问）。

（2）insert的实现

像之前我们已经学习了map和set的insert，其中最大的一个区别就在于map要插入的是key/value，而set是key,那我们怎么用一个树的的模版来完成呢？很简单我们在模版中添加一个类模版即可，我们下面就是map和set在插入涉及内容的类模版

cpp 复制代码 
struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
cpp 复制代码 
struct MapKeyOfT
		{
			const K& operator()(const pair<K,V>& kv)
			{
				return kv.first;
			}
		};

而二叉树的插入操作，我们在前文已经详细解释了，这里不做赘述。有不熟悉的可以看看之前的文章。AVL详解https://blog.csdn.net/2401_85487070/article/details/152172361?fromshare=blogdetail&sharetype=blogdetail&sharerId=152172361&sharerefer=PC&sharesource=2401_85487070&sharefrom=from_link

cpp 复制代码 
pair<Iterator, bool> Insert(const T& data)
	{

		if (_root == nullptr)//将根节点初始化成为黑色
		{
			_root = new Node(data);
			_root->_col = BLACK;

			return { Iterator(_root),true };
		}
		KeyOfT kot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)//遍历到最下方
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return { Iterator(cur),false };//插入失败则返回当前节点
			}
		}

		cur = new Node(data);
		Node* newnode = cur;//保存插入的节点以便于插入后返回时使用
		cur->_col = RED;
		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		if (kot(parent->_data) > kot(data))
		{
			parent->_left = cur;
		}
		cur->_parent = parent;
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (!grandfather) break; // 如果grandfather为空，退出循环
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				//叔叔存在且为红
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					//继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}

				else//叔叔不存在或叔叔为黑,旋转+变色
				{
					if (cur == parent->_left)
					{
						//     g
						//  p    u
						//c 
					//右单旋
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;

					}
					else
					{
						//     g
						//  p     u
						//    c 
						// 左右单旋
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			else//grandfather->_right==parent
			{
				//   g
				// u   p
				Node* uncle = grandfather->_left;
				// 叔叔存在且为红,变色即可
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else // 叔叔不存在，或者存在且为黑
				{
					// 情况二：叔叔不存在或者存在且为黑
					// 旋转+变色
					//   g
					// u   p
					//       c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else//双旋+变色
					{	//    g
						// u     p
						//     c
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}

		}

		_root->_col = BLACK;
		return {Iterator(newnode),true};
	}

其中和之前红黑树的插入删除的主要区别在于首先在插入key/valeu的时候，我们将之前的kv.first

改换成了我们自己的类模版kot，然后就是返回值，增加一个返回指针，便于我们后面的操作。

（3）map的[ ]插入

很显然，像map这种存在key/value结构的树，我们通常会重载一个[ ]来方便我们直接访问其value值，实现原理也很简单

cpp 复制代码 
V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert({ key, V() });
			return ret.first->second;
		}
  • ret.first：就是上面说的迭代器，指向目标键值对（pair<const K, V> 类型）。
  • ->second：通过迭代器访问键值对的 "值"（V 类型），因为迭代器指向的是 pair 对象，-> 用于访问 pair 的成员。
  • 返回引用（V&） ：这是关键 ------ 返回值的引用意味着：
    • 可以直接通过下标修改值（比如 map[1] = "hello"）。
    • 也可以直接读取值（比如 string s = map[1]）。

三、完整代码的实现与测试

RBTree.h

cpp 复制代码 
#pragma once
#include<iostream>
using namespace std;

enum Colour
{
	RED, BLACK
};

template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Colour _col;
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{

	}

};
template<class T,class Ref,class Ptr>
struct TreeIterator
{
	typedef	RBTreeNode<T> Node;
	typedef TreeIterator<T, Ref, Ptr> Self;
	Node* _node;

	TreeIterator(Node* node)
		:_node(node)
	{

	}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return  &_node->_data;
	}

	Self& operator++()
	{
		//当前右孩子不为空，下一个为柚子树中序最左节点
		if (_node->_right)
		{
			Node* min = _node->_right;
				while(min->_left)
				{
					min = min->_left;
				}
			_node = min;
		}
		else	// 当前节点右为空，下一个孩子是父亲左的那个祖先节点
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	Self& operator--()
	{
		if (_node->_left)
		{
			Node* max = _node->_left;
			while (max->_right)
			{
				max = max->_right;
			}
			_node = max;
		}
		else
		{
			
		}

		return *this;
	}

	bool operator!=(const Self& s)const
	{
		return _node != s._node;
	}
	bool operator==(const Self& s)const
	{
		return _node == s._node;
	}

};


template<class K, class T,class KeyOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef TreeIterator<T, T&, T*> Iterator;
	Iterator Begin()
	{
		Node* min = _root;
		while (min && min->_left)
		{
			min = min->_left;
		}
		return Iterator(min);
	}
	Iterator End()
	{
		return Iterator(nullptr);
	}

	pair<Iterator, bool> Insert(const T& data)
	{

		if (_root == nullptr)//将根节点初始化成为黑色
		{
			_root = new Node(data);
			_root->_col = BLACK;

			return { Iterator(_root),true };
		}
		KeyOfT kot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)//遍历到最下方
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return { Iterator(cur),false };//插入失败则返回当前节点
			}
		}

		cur = new Node(data);
		Node* newnode = cur;//保存插入的节点以便于插入后返回时使用
		cur->_col = RED;
		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		if (kot(parent->_data) > kot(data))
		{
			parent->_left = cur;
		}
		cur->_parent = parent;
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (!grandfather) break; // 如果grandfather为空，退出循环
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				//叔叔存在且为红
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					//继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}

				else//叔叔不存在或叔叔为黑,旋转+变色
				{
					if (cur == parent->_left)
					{
						//     g
						//  p    u
						//c 
					//右单旋
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;

					}
					else
					{
						//     g
						//  p     u
						//    c 
						// 左右单旋
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			else//grandfather->_right==parent
			{
				//   g
				// u   p
				Node* uncle = grandfather->_left;
				// 叔叔存在且为红,变色即可
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else // 叔叔不存在，或者存在且为黑
				{
					// 情况二：叔叔不存在或者存在且为黑
					// 旋转+变色
					//   g
					// u   p
					//       c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else//双旋+变色
					{	//    g
						// u     p
						//     c
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}

		}

		_root->_col = BLACK;
		return {Iterator(newnode),true};
	}


	void InOrder()
	{
		_InOrder(_root);

	}
	//bool IsBalance() {
	   // if (_root == nullptr) return true;
	   // if (_root->_col == RED) return false;

	   // // 计算参考值（最左路径黑节点数）
	   // Node* leftMost = _root;
	   // int blackRef = 0;
	   // while (leftMost) {
	   //	 if (leftMost->_col == BLACK) ++blackRef;
	   //	 leftMost = leftMost->_left;
	   // }
	   // return Check(_root, 0, blackRef);
	//}
	bool IsBalance()
	{
		if (_root == nullptr)
			return true;

		if (_root->_col == RED)
			return false;

		// 黑色节点数量参考值
		Node* leftMost = _root;
		int blackRef = 0;
		while (leftMost)
		{
			if (leftMost->_col == BLACK)
				++blackRef;

			leftMost = leftMost->_left;
		}

		return Check(_root, 0, blackRef);
	}

	int Height()
	{
		return _Height(_root);
	}

	int Size()
	{
		return _Size(_root);
	}

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < key)
			{
				cur = cur->_right;
			}
			else if (kot(cur->_data) > key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}


private:
	//bool Check(Node* cur, int blackNum, const int blackRef) {
	//	if (cur == nullptr)
	//		return blackNum == blackRef;  // 修正1：正确判断路径终点

	//	// 修正2：避免根节点访问_parent
	//	if (cur != _root && cur->_col == RED && cur->_parent->_col == RED) {
	//		cout << "连续红节点：" << cur->_kv.first << endl;
	//		return false;
	//	}

	//	// 更新黑节点计数
	//	int newBlackNum = (cur->_col == BLACK) ? blackNum + 1 : blackNum;

	//	// 修正3：独立传递左右子树计数
	//	int leftCount = newBlackNum;
	//	int rightCount = newBlackNum;
	//	bool leftValid = Check(cur->_left, leftCount, blackRef);
	//	bool rightValid = Check(cur->_right, rightCount, blackRef);

	//	return leftValid && rightValid;
	//}
	//	 void _InOrder(Node* root)
	//	 {
	//		 if (root == nullptr)
	//			 return;
	//		 _InOrder(root->_left);
	//		 cout << root->_kv.first<<" ";
	//		 _InOrder(root->_right);
	//	 }


	int _Size(Node* root)
	{
		return root == nullptr ? 0 : _Size(root->_left) + _Size(root->_right) + 1;
	}

	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	bool Check(Node* cur, int blackNum, const int blackNumRef)
	{
		if (cur == nullptr)
		{
			if (blackNum != blackNumRef)
			{
				cout << "黑色节点的数量不相等" << endl;
				return false;
			}

			return true;
		}

		if (cur->_col == RED && cur->_parent && cur->_parent->_col == RED)
		{
			cout << cur->kot(cur->_data) << "->" << "连续的红色节点" << endl;
			return false;
		}

		if (cur->_col == BLACK)
			++blackNum;

		return Check(cur->_left, blackNum, blackNumRef)
			&& Check(cur->_right, blackNum, blackNumRef);
	}
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* parentParent = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subL;
			}
			else
			{
				parentParent->_right = subL;
			}

			subL->_parent = parentParent;
		}
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* parentParent = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parentParent->_left == parent)
			{
				parentParent->_left = subR;
			}
			else
			{
				parentParent->_right = subR;
			}

			subR->_parent = parentParent;
		}
	}

	Node* _root = nullptr;
};

map.h

cpp 复制代码 
#pragma once

#include"RBTree.h"
namespace yiming
{
	template<class K,class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K,V>& kv)
			{
				return kv.first;
			}
		};
	public:
	
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;
		iterator begin()
		{
			return _t.Begin();
		}

		iterator end()
		{
			return _t.End();
		}

		pair<iterator,bool> insert(const pair<K, V>& kv)
		{
			return _t.Insert(kv);
		}
		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert({ key, V() });
			return ret.first->second;
		} 
	private:
		RBTree<K, pair<const K, V>,MapKeyOfT>_t;
	};
}

set.h

cpp 复制代码 
#pragma once
#include"RBTree.h"

namespace yiming
{
	
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};

	public:
		typedef typename RBTree<K, K, SetKeyOfT>::Iterator  iterator;
		iterator begin()
		{
			return _t.Begin();
		}
		iterator end()
		{
			return _t.End();
		}
		pair<iterator,bool> insert(const K& k)
		{
			return _t.Insert(k);
		}
	private:
		RBTree<K,K,SetKeyOfT> _t;
	};
}

test.cpp

cpp 复制代码 
#define _CRT_SECURE_NO_WARNINGS
#include"mymap.h"
#include"myset.h"
void test01()
{
	yiming::set<int> s;
	s.insert(1);
	s.insert(8);
	s.insert(4);
	s.insert(6);
	s.insert(2);
}
void test02()
{
	yiming::set<int> s;
	s.insert(4);
	s.insert(22);
	s.insert(21);
	s.insert(2);
	s.insert(1);
	yiming::set<int>::iterator it = s.begin();
	while (it !=s.end())
	{
		cout << *it << " ";
		++it;
	}
	cout << endl;
}
void test03()
{
	yiming::map<string, string> dict;
	dict.insert({ "sort", "排序" });
	dict.insert({ "left", "左边" });
	dict.insert({ "right", "右边" });

	dict["left"] = "左边，剩余"; // 修改
	dict["insert"] = "插入";  // 插入+修改
	dict["string"];          // 插入

	yiming::map<string, string>::iterator it = dict.begin();
	while (it != dict.end())
	{
		// 不能修改first，可以修改second
		//it->first += 'x';
		it->second += 'x';
		cout << it->first << ":" << it->second << endl;
		++it;
	}
	cout << endl;
}
int main()
{
	test01();
	test02();
	test03();
	
	return 0;
		 
}

测试结果

本次分享就到这里结束了，后续会继续更新，感谢阅读！

相关推荐
消失的旧时光-19433 小时前
ScheduledExecutorService
android·java·开发语言
实心儿儿3 小时前
C++——内存管理
c++
山，离天三尺三3 小时前
深度拷贝详解
开发语言·c++·算法
SpiderPex4 小时前
论MyBatis和JPA权威性
java·mybatis
future_studio4 小时前
聊聊 Unity（小白专享、C# 小程序 之 加密存储）
开发语言·小程序·c#
一只鱼^_4 小时前
第 167 场双周赛 / 第 471 场周赛
数据结构·b树·算法·leetcode·深度优先·近邻算法·迭代加深
我狸才不是赔钱货4 小时前
容器：软件世界的标准集装箱
linux·运维·c++·docker·容器
Seeing54 小时前
数据结构----树
数据结构
云知谷4 小时前
【嵌入式基本功】单片机嵌入式学习路线
linux·c语言·c++·单片机·嵌入式硬件
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04Linux下V2Ray安装配置指南05GitLab 零基础入门指南：从安装到项目管理全流程06两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答07KGG转MP3工具|非KGM文件|解密音频082025软件测试面试八股文（含答案+文档）09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）