[优选算法专题四.前缀和——NO.26二维前缀和]

题目链接：

二维前缀和

题目描述：

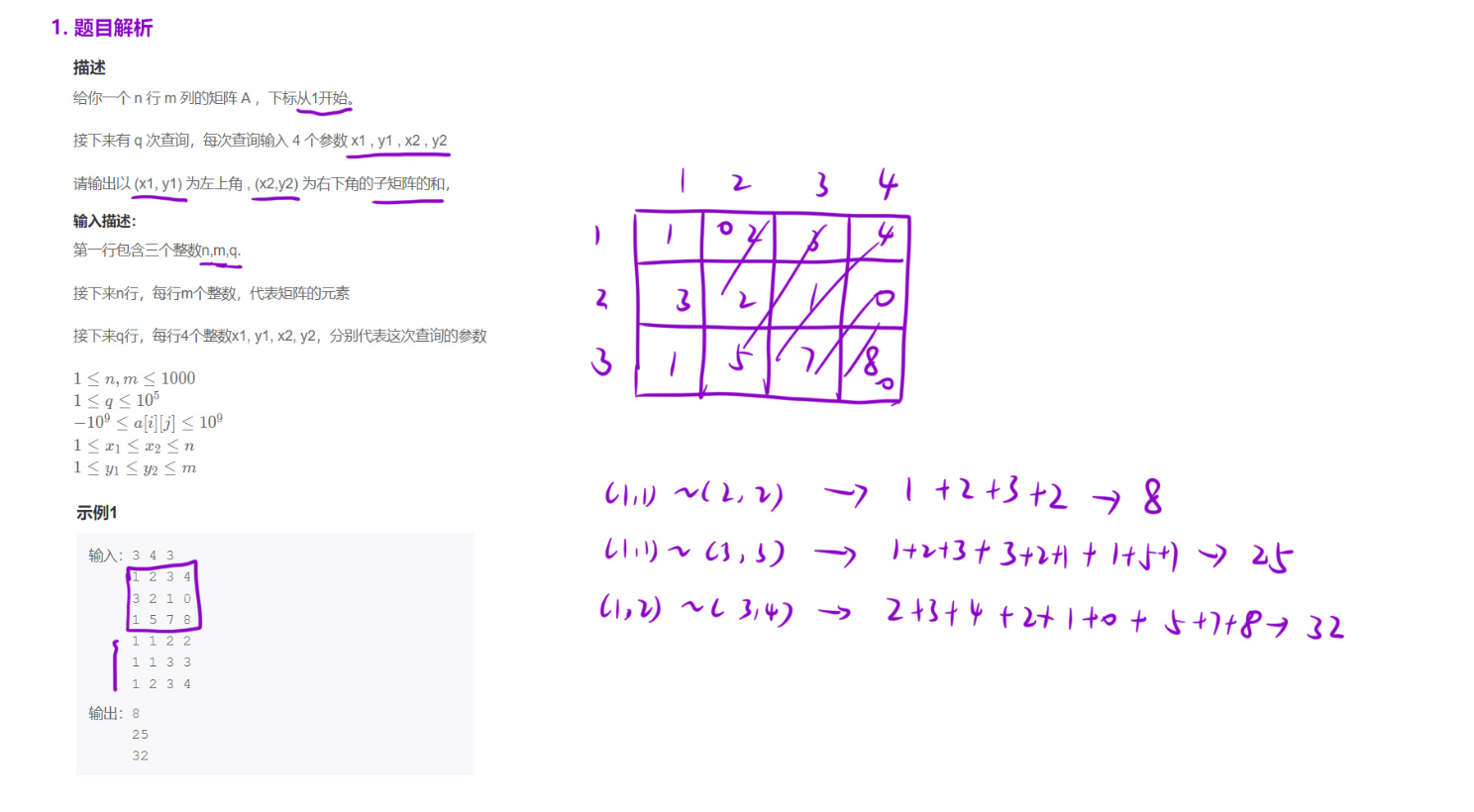
题目解析：

---

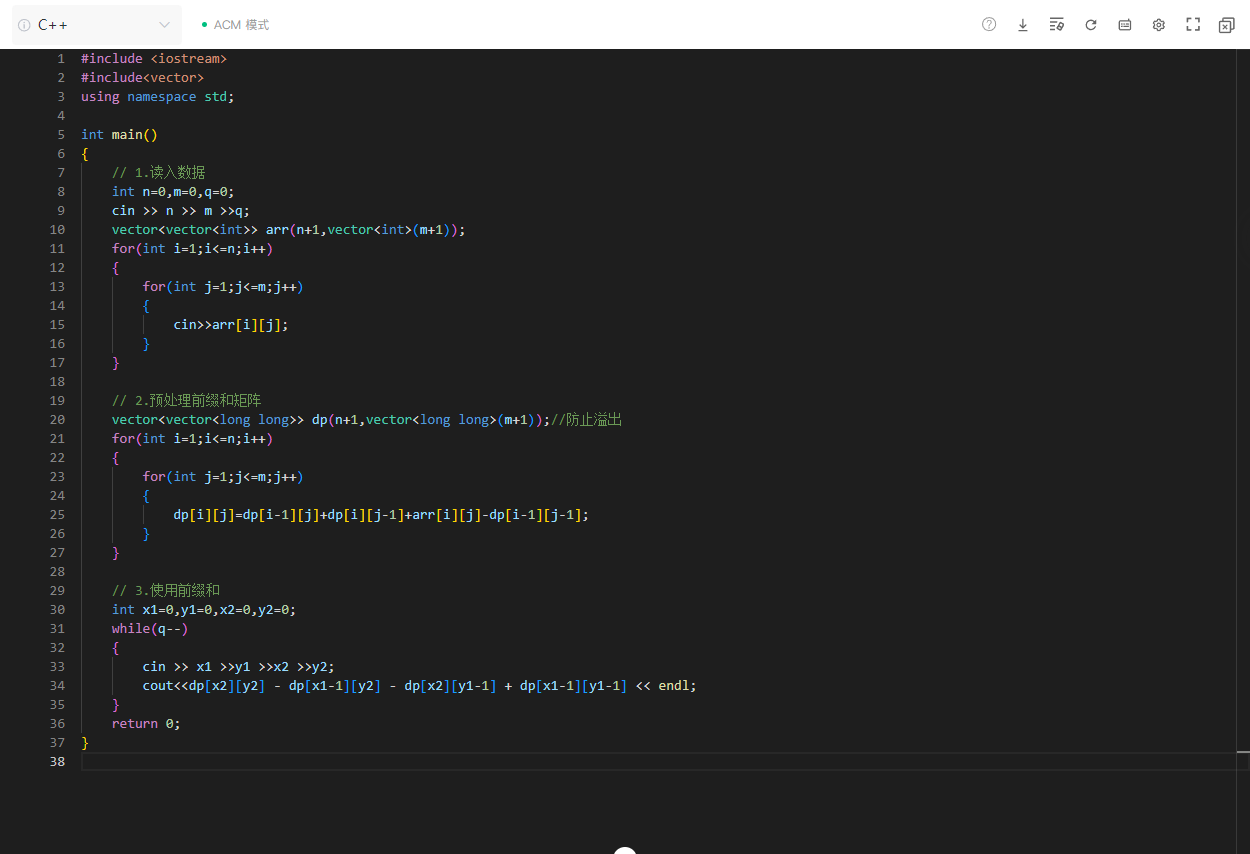
代码逐部分解析

读入原始数据

int n = 0, m = 0, q = 0;
cin >> n >> m >> q;
vector<vector<int>> arr(n + 1, vector<int>(m + 1));
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        cin >> arr[i][j];
    }
}

• n：二维数组的行数，m：列数，q：查询次数。
• 定义二维数组 arr，大小为 (n+1)×(m+1)，下标从 1 开始（方便前缀和计算，避免处理边界时的额外判断）。
• 双层循环读入 n×m 个元素，存储到 arr 中。

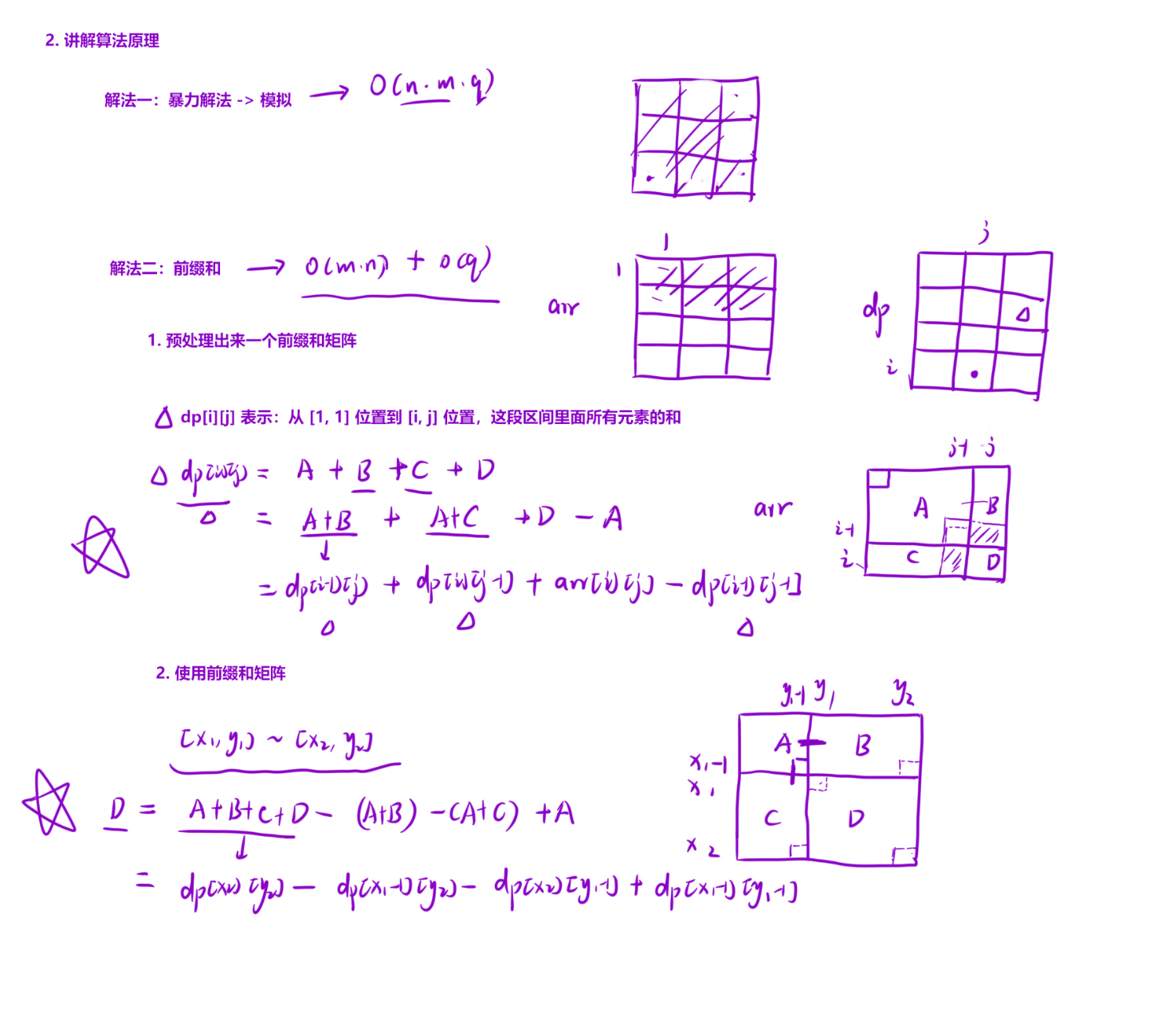
预处理前缀和矩阵 dp

vector<vector<long long>> dp(n + 1, vector<long long>(m + 1)); // 防止溢出
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];
    }
}

• dp 是前缀和矩阵，类型为 long long（避免多个整数累加时溢出）。
• dp[i][j] 表示：以 arr[1][1] 为左上角、arr[i][j] 为右下角的矩形区域的所有元素之和。
• 计算公式推导 ：dp[i][j] = 上方区域和（dp[i-1][j]） + 左方区域和（dp[i][j-1]） + 当前元素（arr[i][j]） - 重复计算的左上角区域和（dp[i-1][j-1]）。（画图理解更直观：上方和左方区域重叠的部分被加了两次，需要减去一次）。

处理查询并输出结果

int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
while (q--) {
    cin >> x1 >> y1 >> x2 >> y2;
    cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;
}

• 每次查询输入矩形的左上角坐标 (x1, y1) 和右下角坐标 (x2, y2)。
• 区域和计算公式 ：目标区域和 = 大矩形和（dp[x2][y2]） - 上方多余区域（dp[x1-1][y2]） - 左方多余区域（dp[x2][y1-1]） + 重复减去的左上角区域（dp[x1-1][y1-1]）。（同样通过画图可清晰理解：减去上方和左方后，左上角重叠部分被多减了一次，需要加回）。

总结

• 时间复杂度 ：预处理前缀和为 O(n*m)，每次查询为 O(1)，总复杂度为 O(n*m + q)，适合大量查询的场景。
• 空间复杂度 ：O(n*m)（存储原始数组和前缀和矩阵）。
• 关键点 ：数组下标从 1 开始简化边界处理，使用 long long 避免整数溢出。