1 实验一
1.1 实验题目
(1) 计算一幅图像的熵。
(2) 用霍夫曼编码压缩图像,并显示压缩前后图像。
(3) 计算霍夫曼编码的压缩率和效率。
(4) 考虑对相邻像素的差值编码。新差值图像的熵是多少?
1.2 程序源代码
Matlab
% 计算熵
clear,clc,close ALL;
tic
f1=imread('photo.jpg');
n=256;
%计算图的熵
x1=double(f1);
P1=hist(x1(:),n);
P1=P1/sum(P1(:));
i1=find(P1);
h1=-sum(P1(i1).*log2(P1(i1)));
figure;
subplot(111),imshow(f1),title(['图 1 的熵为:',num2str(h1)]);
toc
I = imread('photo.jpg');
I = imresize(I,0.1); %将图像大小缩小(可以不缩小,但是用 matlab 进行编译会花很长时间)
[M,N] = size(I); %将读取的图像转为二维矩阵
I1 = I(:); %转为一维向量
P = zeros(1,256);
%获取各符号的概率;
for i = 0:255
P(i+1) = length(find(I1 == i))/(M*N);
end
k = 0:255;
dict = huffmandict(k,P); %生成字典
enco = huffmanenco(I1,dict); %编码
deco = huffmandeco(enco,dict); %解码
Ide = col2im(deco,[M,N],[M,N],'distinct'); %把向量重新转换成图像块;
figure;
subplot(1,2,1);imshow(I);title('original image');
subplot(1,2,2);imshow(uint8(Ide));title('deco image')1.3 计算公式
编码压缩效率=等长码所占内存/哈夫曼编码所占内存
2 实验二
2.1 实验题目
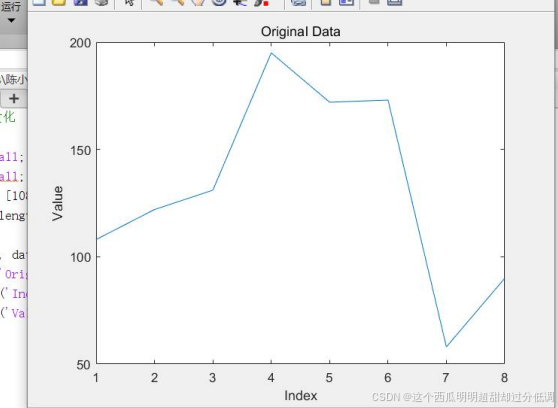
考虑一列数据{108,122,131,195,172,173,58,90}。若用 4 比特精度来均匀量化它,计 算量化后数据的均方根误差,给出量化前后的曲线图(plot 函数)。
2.2 程序源代码
Matlab
%均匀量化
clc;
close all;
clear all;
%量化前的数据曲线图
data = [108,122,131,195,172,173,58,90];
x = 1:length(data);
plot(x, data);
title('Original Data');
xlabel('Index');
ylabel('Value');
%进行均匀量化
quantized_data = round(data / (max(data) - min(data)) * 15);
%计算均方根误差
mse = sqrt(mean((data - quantized_data).^2));
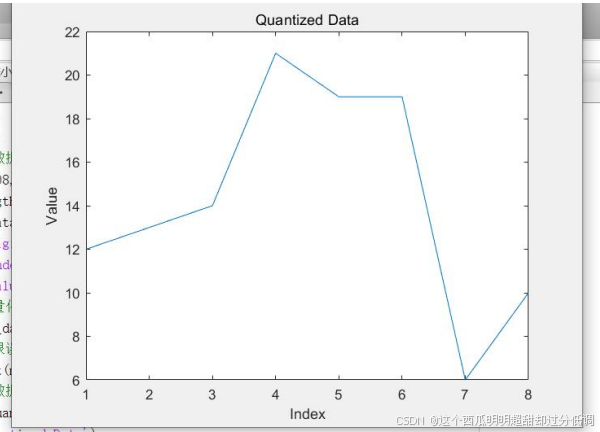
%量化后的数据曲线图
plot(x, quantized_data);
title('Quantized Data');
xlabel('Index');
ylabel('Value');2.3 实验结果