文章目录
前言
本文介绍了邻接矩阵在图论中的定义与应用。文章首先给出了邻接矩阵的标准数学定义,说明如何用0/1矩阵表示顶点间的连接关系。通过无向图和有向图的具体示例,详细讲解了邻接矩阵的构建方法及其C语言实现代码。重点阐述了如何利用邻接矩阵求取顶点的度、入度和出度,并分析了时间复杂度。此外,文章还介绍了带权图的邻接矩阵表示法,探讨了邻接矩阵的空间复杂度、适用场景(稠密图)和对称性质。最后,说明了邻接矩阵的数学性质,即矩阵幂次与路径数的关系,并总结了邻接矩阵的优缺点及重要考点。全文系统性地介绍了邻接矩阵的理论基础和实践应用。
一.标准定义
- 结点数为 n 的图 G=(V,E) 的邻接矩阵 A 是 n\times n 的。将 G 的顶点编号为 v_{1},v_{2},\dotsc ,v_{n},则
A [ i ] [ j ] = { 1 , 若 ( v i , v j ) 或 < v i , v j > 是 E ( G ) 中的边 0 , 若 ( v i , v j ) 或 < v i , v j > 不是 E ( G ) 中的边 A[i][j]=\begin{cases}1,&\text{若}(v_{i},v_{j})\text{或}< v_{i},v_{j}>\text{是}E(G)\text{中的边} \\ 0,&\text{若}(v_{i},v_{j})\text{或}< v_{i},v_{j}>\text{不是}E(G)\text{中的边}\end{cases} A[i][j]={1,0,若(vi,vj)或<vi,vj>是E(G)中的边若(vi,vj)或<vi,vj>不是E(G)中的边
二.方法说明
- 用一个矩阵存储两个元素之间是否存在直接相连的边,如果有,则为1,没有则为0
- 0表示的是两个顶点之间相互不连接,而1表示的是两个顶点之间相互是连接的
1.举例子
1.无向图
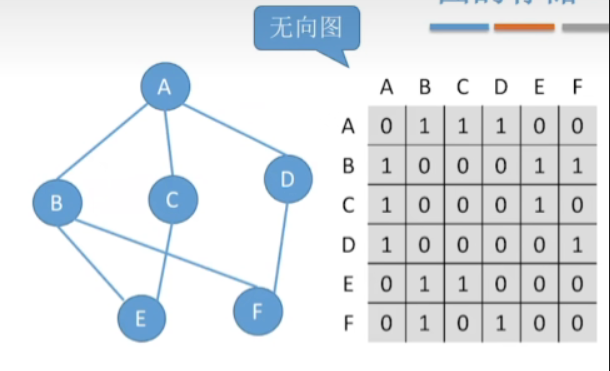
- 例如A到D之间有直接相连的一条边,则在A和D对应的方框中填1,A到F之间没有直接相连的边,则在A和F的队友方框填0
- 以此类推
2.有向图
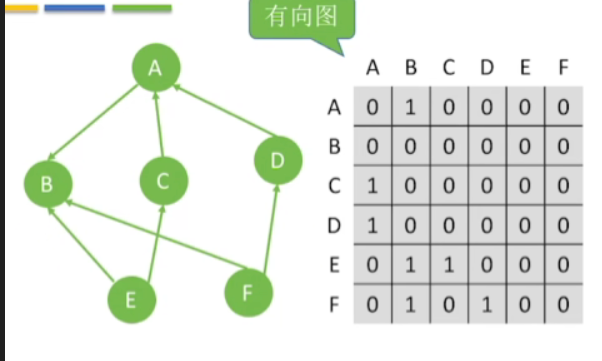
- A可以直接到达B,则A和B的方框中(有顺序),应该填写1
- B不能直接到达A,则B和A的方框中(有顺序),应该填写0
4.代码实现
c
#define MaxVertexNum 100
typedef struct{
char Vex[MaxVertexNum]; //顶点数目的最大值
int Edge[MaxVertexNum][MaxVertexNum]; //顶点表
int vexnum,arcnum; //邻接矩阵,边表
}MGraph;三.求度,入度,出度
1.无向图求度
1.步骤
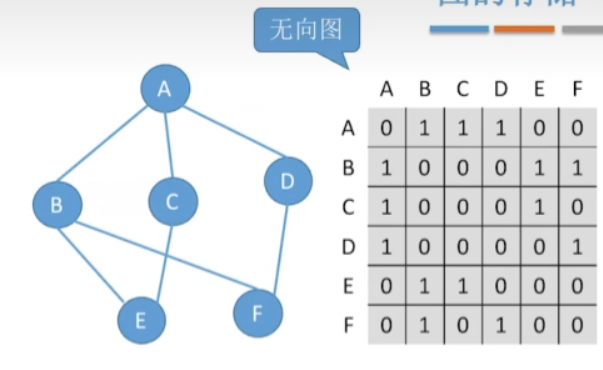
- 要求指定节点B的度
- 我们可以检查一下和B相对应的这一整行总共有几个非零元素
- 那总共应该是有三个,所以B的度就应该是3
- 另外我们也可以检查和b相对应的这一列总共有几个非零元素
- 那同样的也是有三个
2.结论
- 对于无线图来说求顶点的度,我们可以遍历和它所对应的那一行或者那一列检查非零元素的个数
- 第i个结点的度 = ==第i行(或第i列)==的非零元素个数
2.有向图
1.步骤
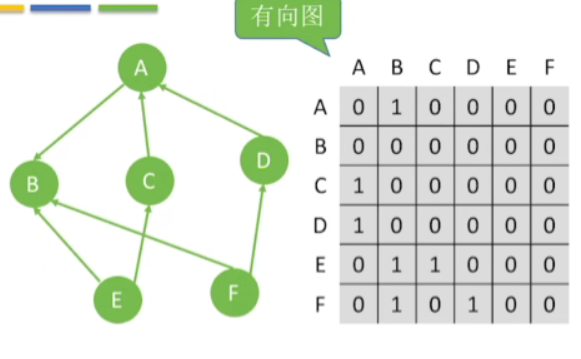
- 指定A这个节点
- 要求A这个节点的出度,应该求的是和A相对应的一整行当中有几个非零元素
- 要求A这个节点的入度,应该求的是和A相对应的一整列当中有几个非零元素
- 而有向图中顶点的度等于入度加出度,所以求这个顶点的度,我们只需要把与之对应的这一行和这一列所有非零元素的个数进行一个加和就可以
2.结论
- 第i个结点的出度 = 第i行的非零元素个数
- 第i个结点的入度 = 第i列的非零元素个数
- 第i个结点的度 = 第i行、第i列的非零元素个数之和
- 邻接矩阵法求顶点的度/出度/入度的时间复杂度都为O(|V|)
四.邻接矩阵法存储带权图(网)
1.思路
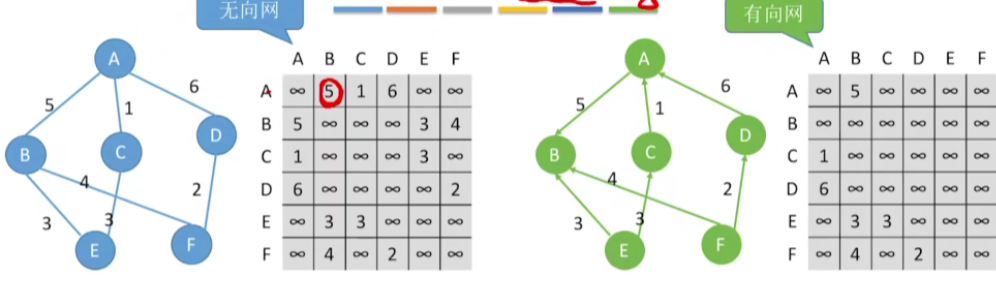
- 只需要在对应的位置给它写上这两个顶点之间的这条边的一个权值就可以
- 而如果两个顶点之间不存在边的话,那么我们可以用这种无穷来表示它们之间不存在相连的边
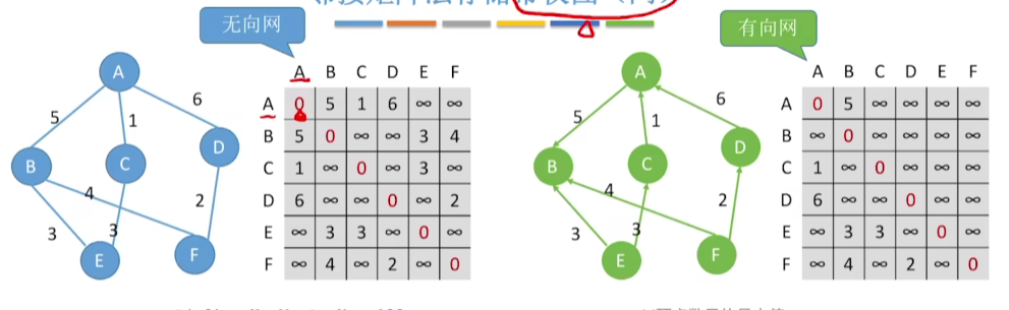
- 有的人也会把就是自己指向自己的这条边的权值设为0
2.代码
c
#define MaxVertexNum 100//顶点数目的最大值
//可用int的上限值表示"无穷"
#define INFINITY 最大的int值//宏定义常量"无穷"
typedef char VertexType;//顶点的数据类型
typedef int EdgeTyppe;//带权图中边上权值的数据类型
typedef struct{
VertexType Vex[MaxVertexNum];//顶点
EdgeType Edge[MaxVertexNum];//边的权
int vexnum, arcnum;//图的当前顶点树和弧树
}MGraph五.邻接矩阵法的性能分析
- 空间复杂度:O(|V|²)------只和顶点数相关,和实际的边数无关
- 适合用于存储稠密图
- 无向图的邻接矩阵是对称矩阵,可以压缩存储(只存储上三角区/下三角区)
六.邻接矩阵法的性质(矩阵不带权值)
1.理论
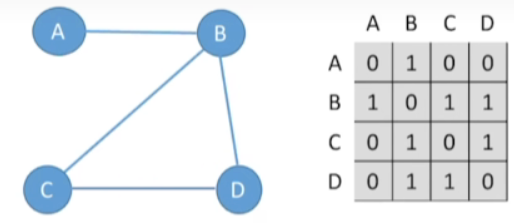
- 设图G的邻接矩阵为A (矩阵元素为(0/1),则 A n A^{n} An的元素 A n [ i ] [ j ] A^n[i][j] An[i][j]等于由顶点i到顶点j的长度为n的路径的数目
2.举例说明
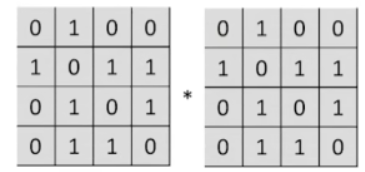
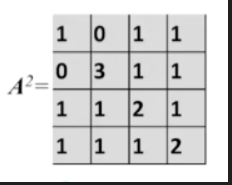
- 计算在路径长度为2的情况下,从A到D有多少条路径?
- A 2 [ 1 ] [ 4 ] = a 1 , 1 a 1 , 4 + a 1 , 2 a 2 , 4 + a 1 , 3 a 3 , 4 + a 1 , 4 a 4 , 4 = 1 A^{2}[1]\left[4\right]=a_{1,1}a_{1,4}+a_{1,2}a_{2,4}+a_{1,3}a_{3,4}+a_{1,4}a_{4,4}=1 A2[1][4]=a1,1a1,4+a1,2a2,4+a1,3a3,4+a1,4a4,4=1
- 这个式子当中, a 1 , 2 a_{1,2} a1,2的值为1,表示从A到B有一条路径, a 2 , 4 a_{2,4} a2,4的值为1,表示从B到D有一条路径
- 它们相乘等于1,说明,我们可以找到一条路径从A到D,这条路径是先从A到B再从B到D
- 其他式子也是这样理解
- 最终得到的 A 2 [ 1 ] [ 4 ] A^2[1][4] A2[1][4]这个式子的值指的是,我们从A到D在路径长度为2的情况下,只能找到一条符合这个条件的路径
- 计算在路径长度为2的情况下,从B到B有多少条路径?
- A 2 [ 2 ] [ 2 ] = a 2 , 1 a 1 , 2 + a 2 , 2 a 2 , 2 + a 2 , 3 a 3 , 2 + a 2 , 4 a 4 , 2 = 3 A²[2][2]=a_{2,1}a_{1,2}+a_{2,2}a_{2,2}+a_{2,3}a_{3,2}+a_{2,4}a_{4,2}=3 A2[2][2]=a2,1a1,2+a2,2a2,2+a2,3a3,2+a2,4a4,2=3
- 与上面的式子是一样的理解方式
- 在路径长度为2的情况下,各个元素之间有多少条路径?
- A 2 [ 3 ] [ 3 ] = a 3 , 1 a 1 , 3 + a 3 , 2 a 2 , 3 + a 3 , 3 a 3 , 3 + a 3 , 4 a 4 , 3 = 1 A^{2}[3][3]=a_{3,1}a_{1,3}+a_{3,2}a_{2,3}+a_{3,3}a_{3,3}+a_{3,4}a_{4,3}=1 A2[3][3]=a3,1a1,3+a3,2a2,3+a3,3a3,3+a3,4a4,3=1
- A 2 [ 1 ] [ 2 ] = a 1 , 1 a 1 , 2 + a 1 , 2 a 2 , 2 + a 1 , 3 a 3 , 2 + a 1 , 4 a 4 , 2 = 0 A^{2}[1][2]=a_{1,1}a_{1,2}+a_{1,2}a_{2,2}+a_{1,3}a_{3,2}+a_{1,4}a_{4,2}=0 A2[1][2]=a1,1a1,2+a1,2a2,2+a1,3a3,2+a1,4a4,2=0
七.知识回顾与重要考点
- 数组实现的顺序存储,空间复杂度高,不适合存储稀疏图

结语
一更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页