19.map和set的封装

liu****2025-10-21 10:01

总的代码会放在最后面

一.set和map源码分析

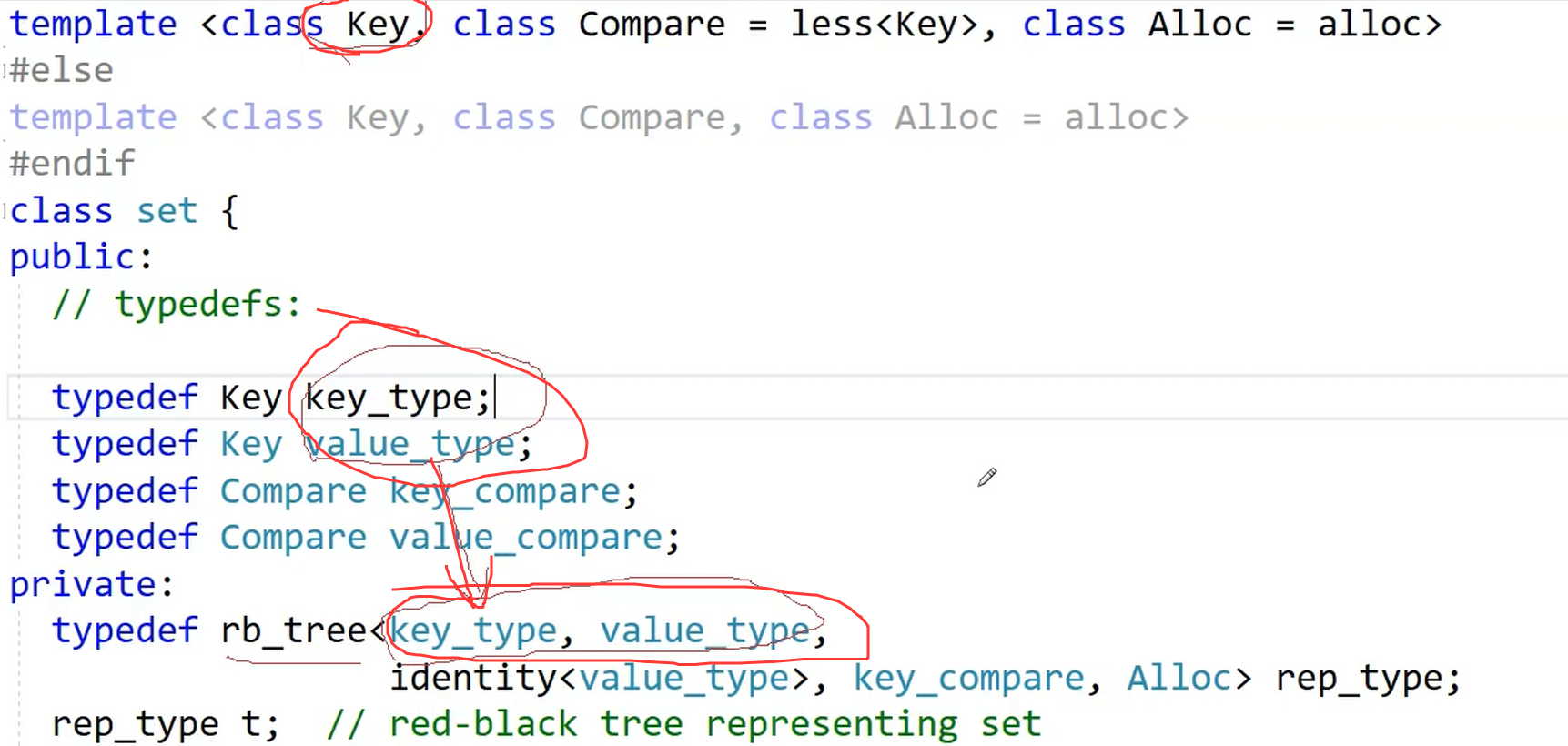
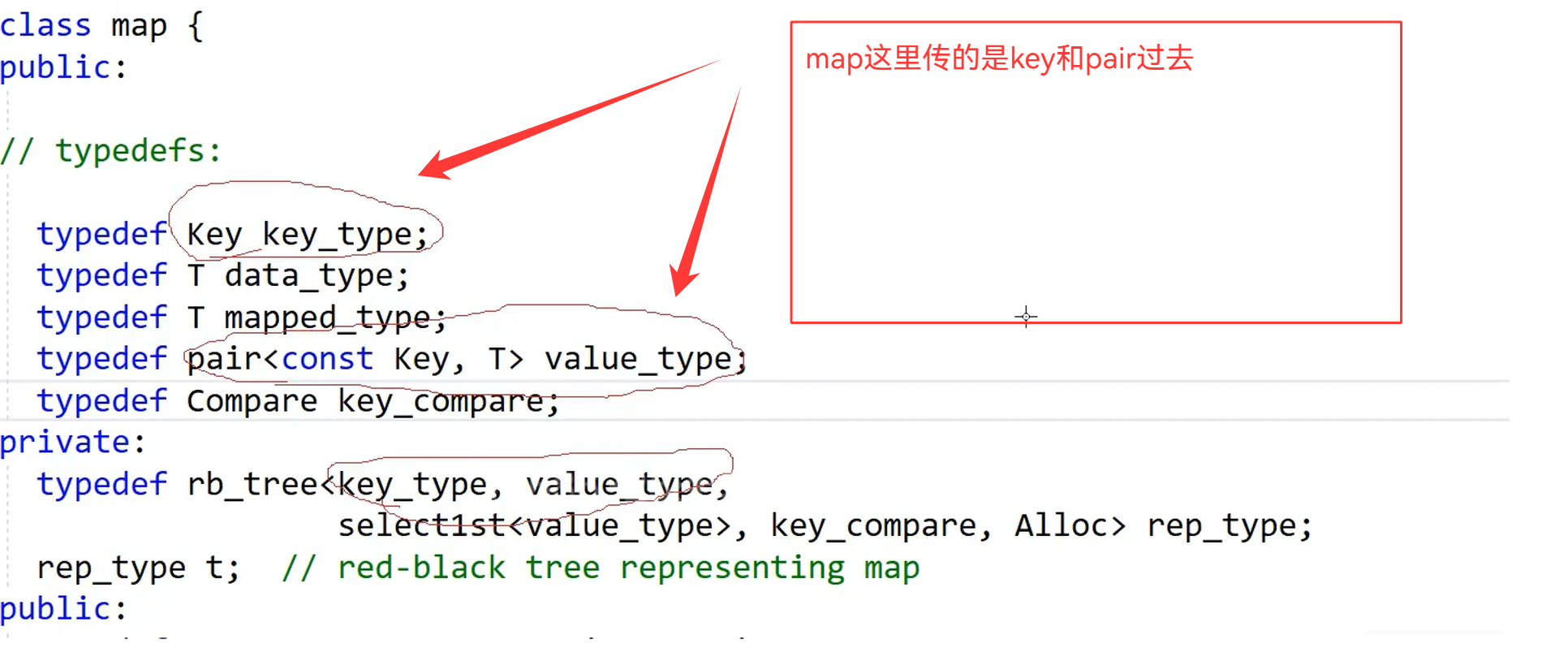
我们根据这里的map和set发现,他们传入的要么是(key,key)或者是(key,pair(key,T))

第一个模板参数传入的都是key,就第二个模板参数有问题(这个地方是关键)

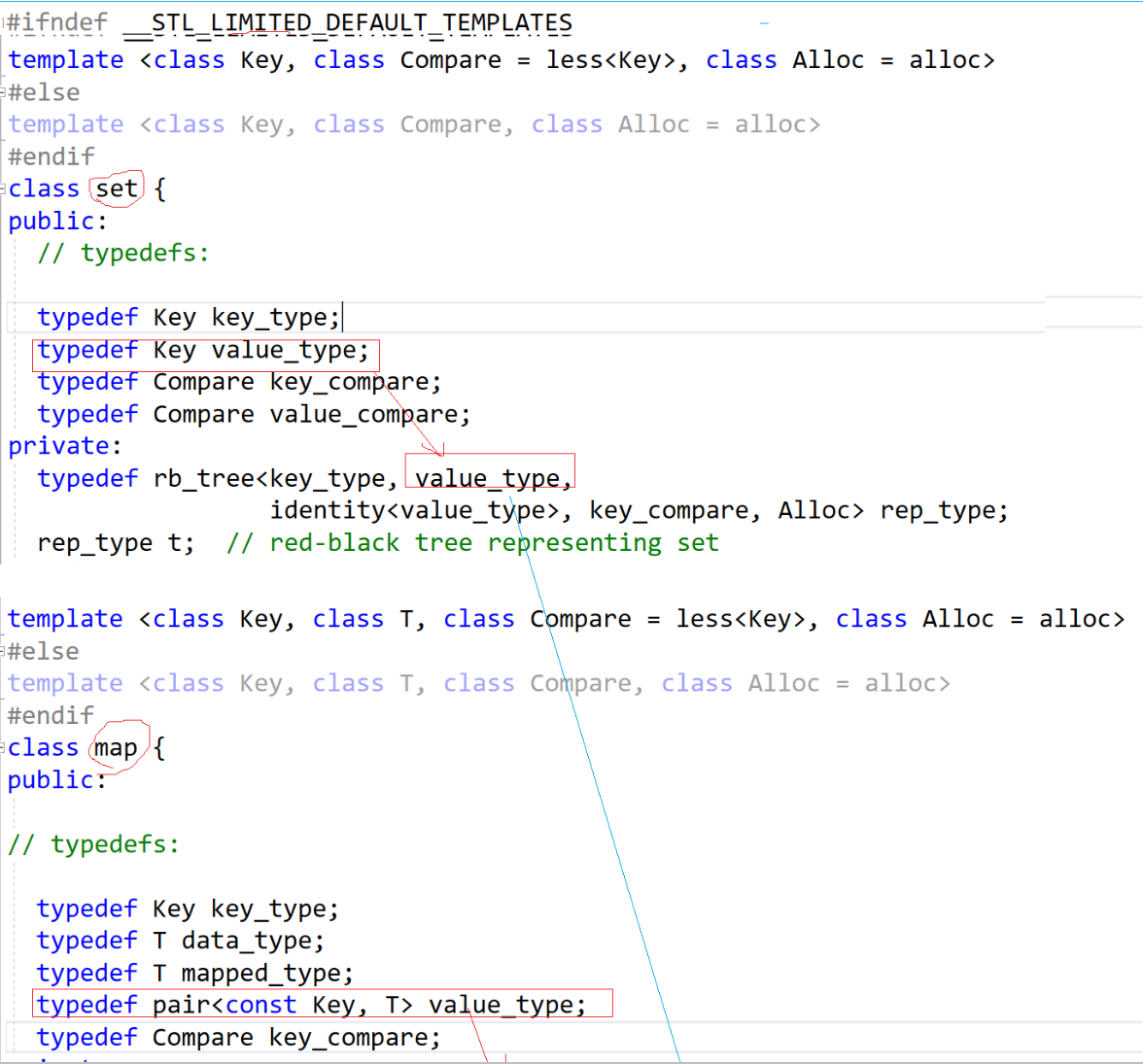
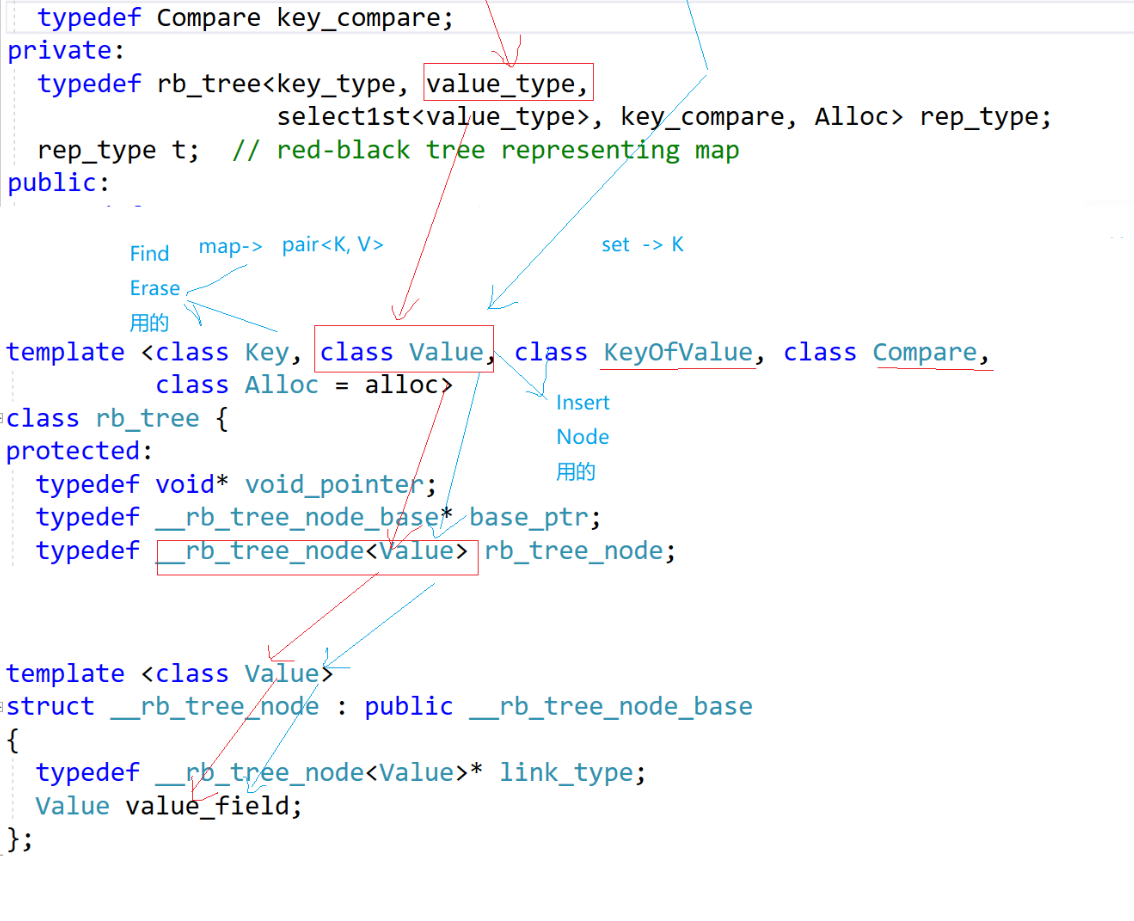
我们可以发现这个地方和我们写的不一样,这里他用的是一个RBTree进行使用,set和map是通过模板参数进行使用

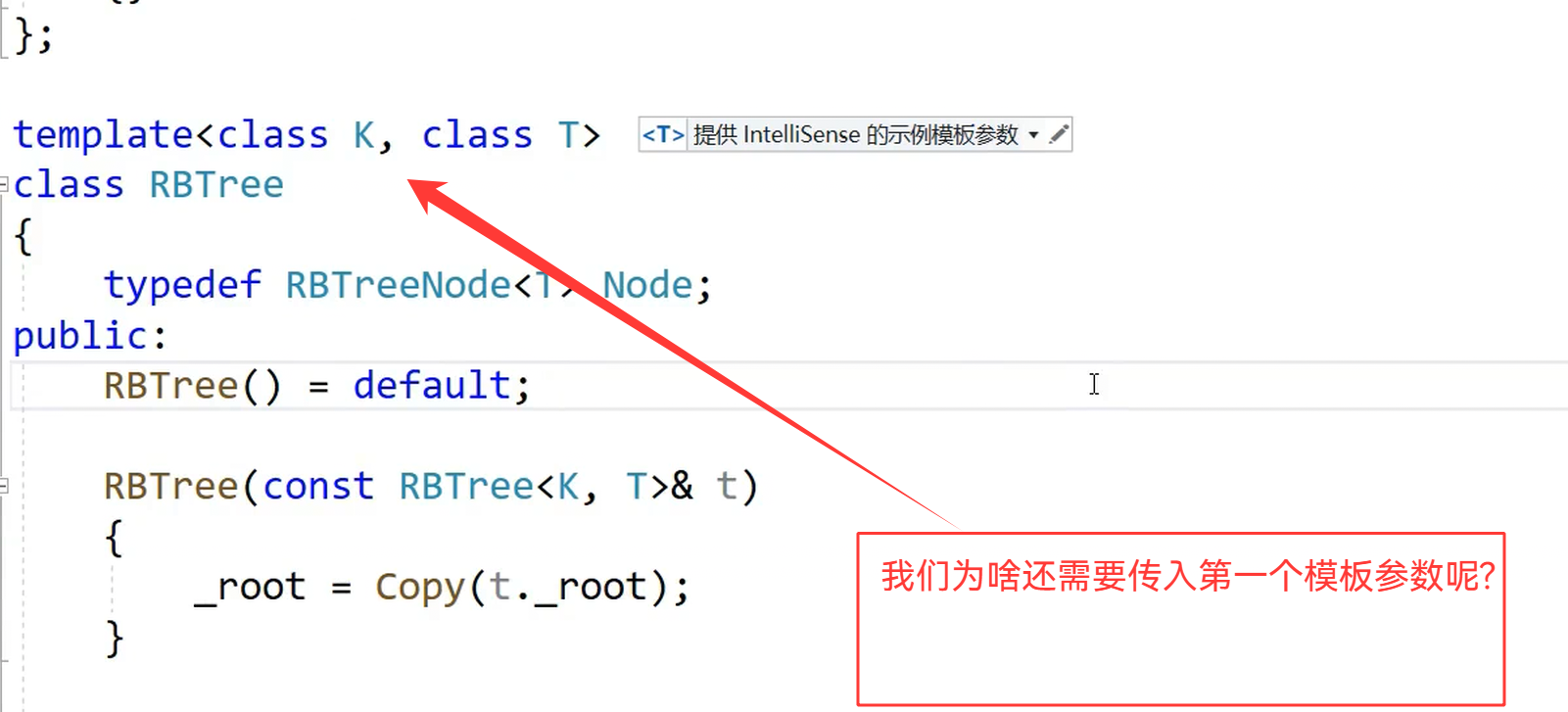
一个传入的是(key,key) , 另一个传入的是(key,pair<key,T>)

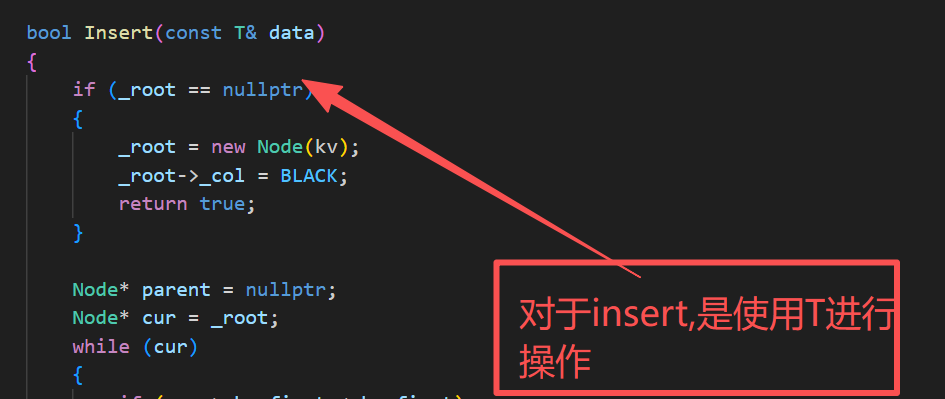
所以说,第一个参数是给find和erase使用的

二.实现set和map的框架

cpp 复制代码 
"set实现"

#pragma once

#include "RBTree(copy).h"


namespace ltw
{
    template<class K>
    class set
    {

    private:
        RBTree<K,K> _t;
    };
}
cpp 复制代码 
"map实现"



#pragma once

#include "RBTree(copy).h"

namespace ltw
{
    template<class K,class V>
    class map
    {
   
    private:
        RBTree<K,pair<K,V>> _t;
    };
}

三.插入的复用

cpp 复制代码 
#pragma once

#include "RBTree(copy).h"


namespace ltw
{
    template<class K>
    class set
    {
    public:
        bool Insert(const K& key)
        {
            _t.Insert(key);
        }
    private:
        RBTree<K,K> _t;
    };
}
cpp 复制代码 
#pragma once

#include "RBTree(copy).h"

namespace ltw
{
    template<class K,class V>
    class map
    {
    public:
        bool Insert(const pair<K,V>& kv)
        {
            _t.Insert(kv);
        }
    private:
        RBTree<K,pair<K,V>> _t;
    };
}

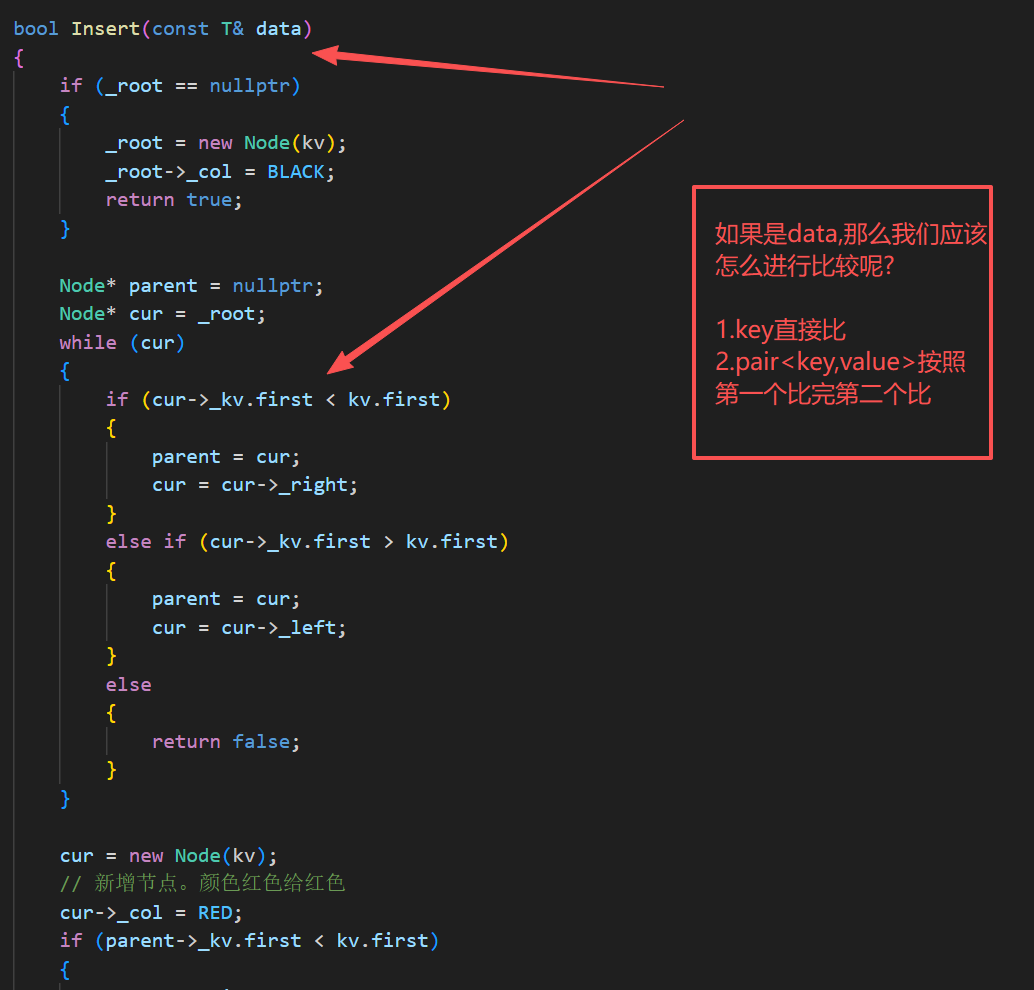
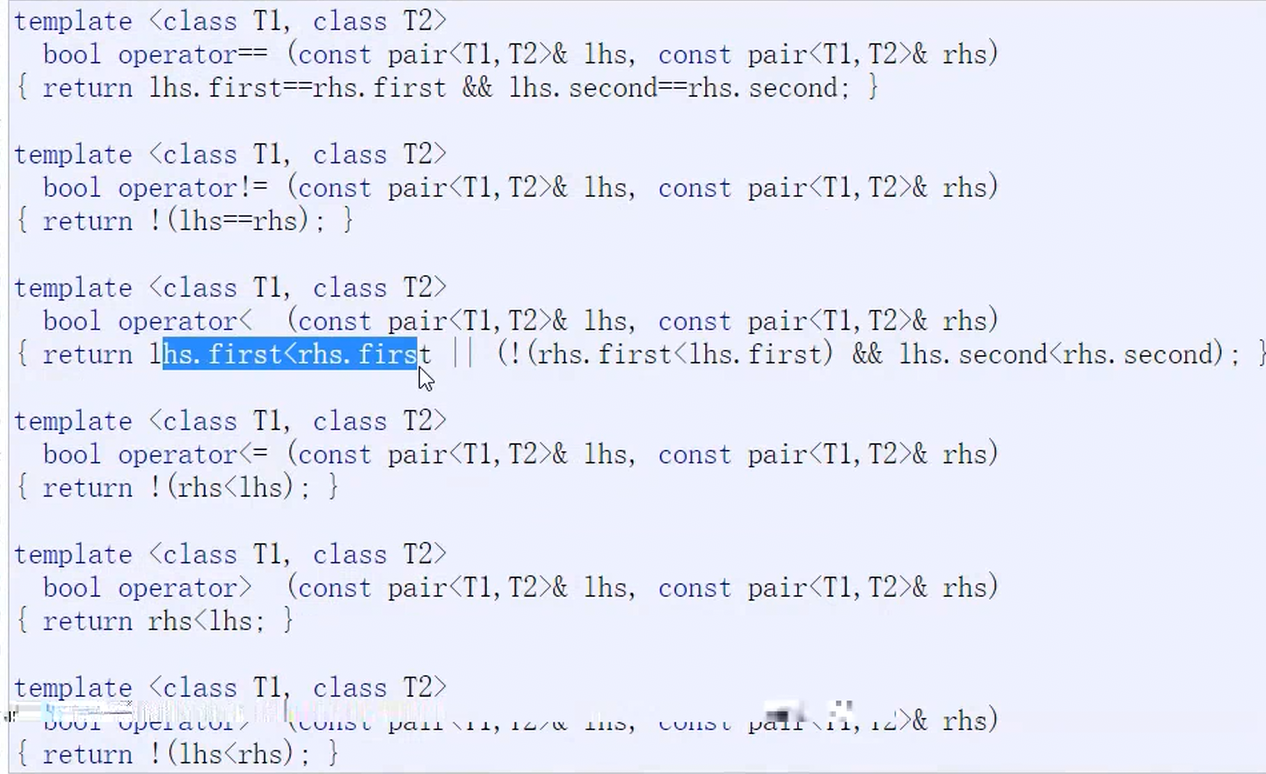
但是这里我们只要第一个进行比较

所以对于红黑树这一层,我们不知道,传入的到底是key还是pair<>,但是我们的上层知道啊

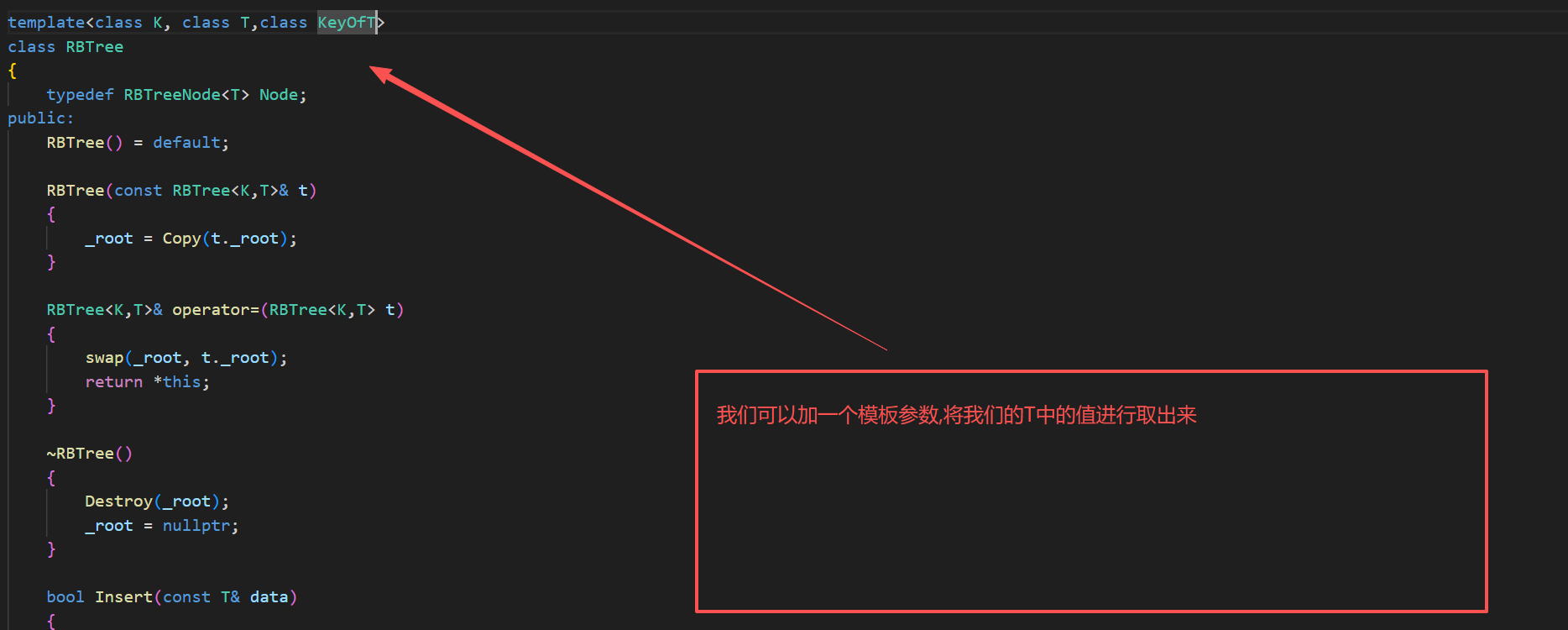
我们通过传入我们的模板参数,然后进行实例化,拿到值即可

cpp 复制代码 
#pragma once

#include "RBTree(copy).h"

namespace ltw
{
    template<class K,class V>
    class map
    {
        struct MapKeyOfT
        {
            const K& operator()(const pair<K,V>& kv)
            {
                return kv.first;
            }
        };
    public:
        bool Insert(const pair<K,V>& kv)
        {
            _t.Insert(kv);
        }
    private:
        RBTree<K,pair<K,V>,MapKeyOfT> _t;
    };
}
cpp 复制代码 
#pragma once

#include "RBTree(copy).h"


namespace ltw
{
    template<class K>
    class set
    {
        struct SetKeyOfT
        {
            const K& operator()(const K& key)
            {
                return key;
            }
        };
    public:
        bool Insert(const K& key)
        {
            _t.Insert(key);
        }
    private:
        RBTree<K,K,SetKeyOfT> _t;
    };
}

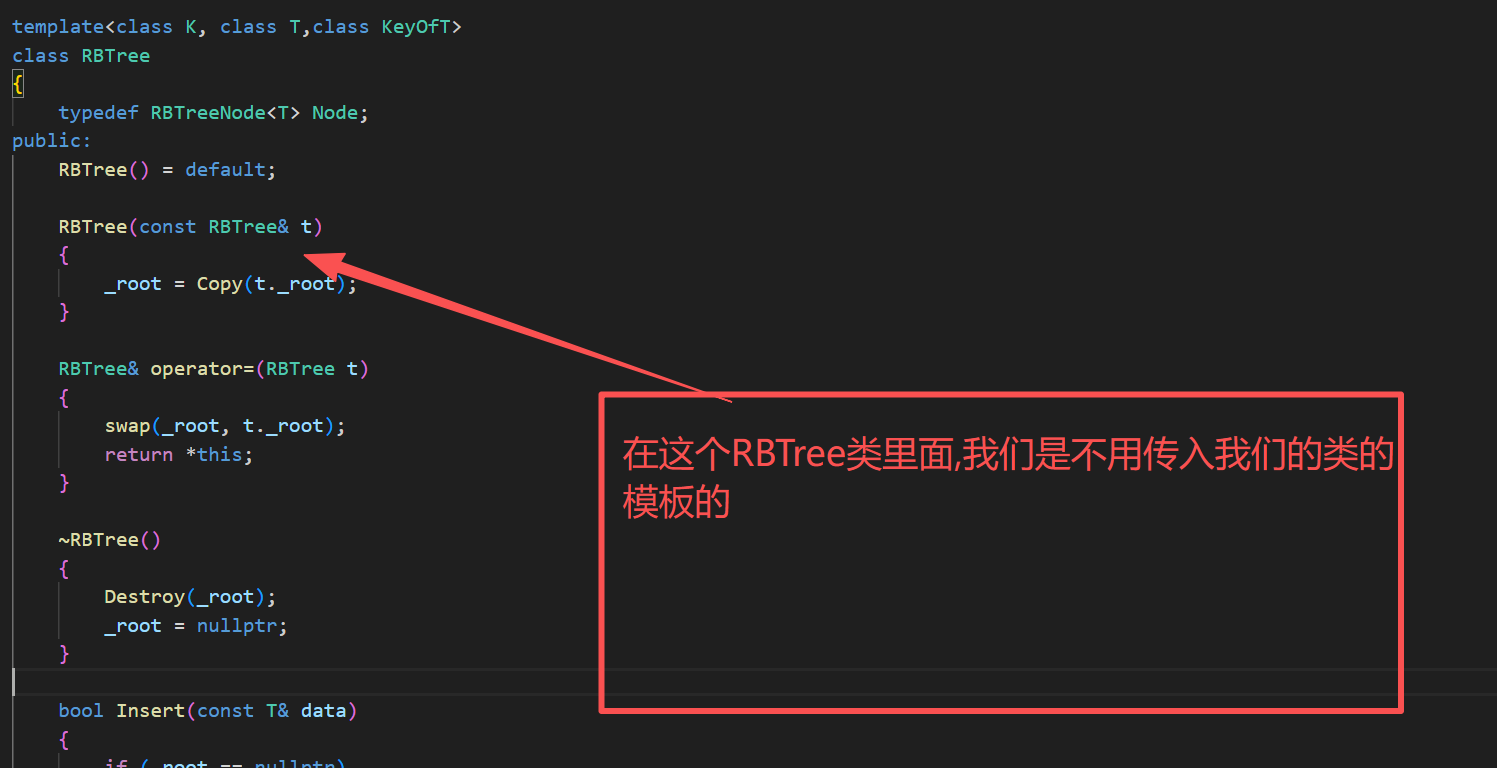
Insert的实现如下:

cpp 复制代码 
bool Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return true;
		}

		KeyOfT kot;

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(data);
		// 新增节点。颜色红色给红色
		cur->_col = RED;
		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		cur->_parent = parent;

        while(parent && parent->_col == RED)
        {
            Node* grandfather = parent->_parent;
            if(parent == grandfather->_left)
            {
                //       g
                //   p       u
                Node* uncle = grandfather->_right;
                if(uncle && uncle->_col == RED)
                {
                    //叔叔存在且为红  -> 变色+向上处理
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;
                }
                else
                {
                    //叔叔存在且为黑/不存在  -> 变色+向上处理
                    if(cur == parent->_left)
                    {
                        //     g
                        //   p    u
                        // c
                        // 单旋
                        RotateR(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    else
                    {
                        //      g
                        //   p     u
                        //     c
                        //双旋
                        RotateL(parent);
                        RotateR(grandfather);
                        cur->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    break;
                }
            }
            else
            {
                //       g
                //   u       p
                Node* uncle = grandfather->_left;
                if(uncle && uncle->_col == RED)
                {
                    //叔叔存在且为红  -> 变色+向上处理
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;
                }
                else
                {
                    //叔叔存在且为黑/不存在  -> 变色+向上处理
                    if(cur == parent->_right)
                    {
                        //     g
                        //   u    p
                        //           c
                        // 单旋
                        RotateL(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    else
                    {
                        //      g
                        //   u     p
                        //       c
                        //双旋
                        RotateR(parent);
                        RotateL(grandfather);
                        cur->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    break;
                }
            }
        }
        _root->_col = BLACK;

		return true;
	}

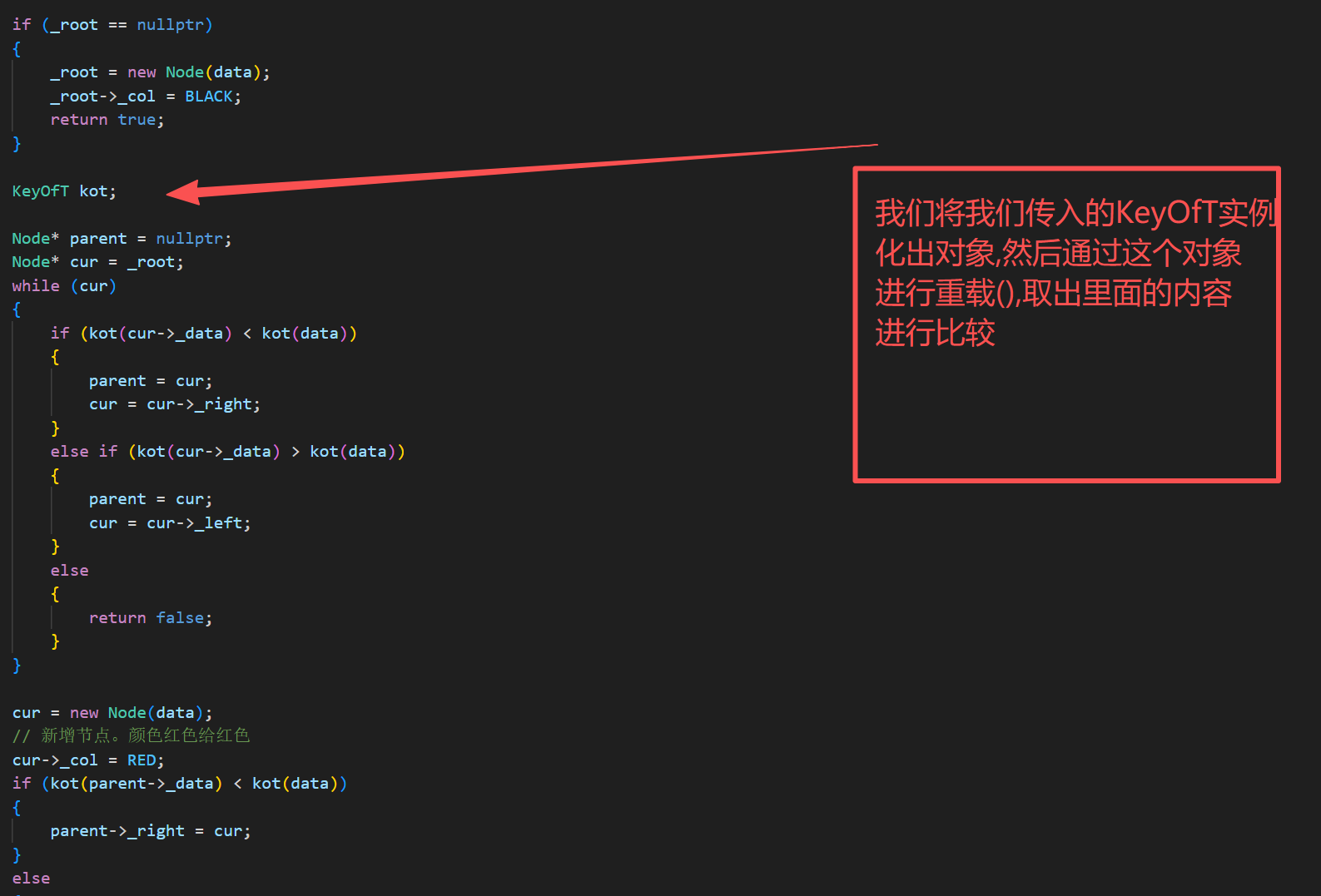
本质上就是回调

四.测试代码

cpp 复制代码 
void test_set()
    {
        set<int> s;
        int a[] = {4,2,6,1,3,5,15,7,16,14};
        for(auto e:a)
        {
            s.insert(e);
        }
    }

我们插入一点数据进行测试一下,发现没有报错,那么说明我们模板部分没有写错

五.红黑树迭代器的实现

1.简单 *, !=等操作符 的实现

cpp 复制代码 
template <class K,class T>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<K,T> Self;

	Node* _node;

	RBTreeIterator(Node* node)
		:_node(node)
	{

	}

	T& operator*()
	{
		return _node->_data;
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}

};

这些简单的部分,我们就不做过多的介绍了

2.把迭代器加入到红黑树里面

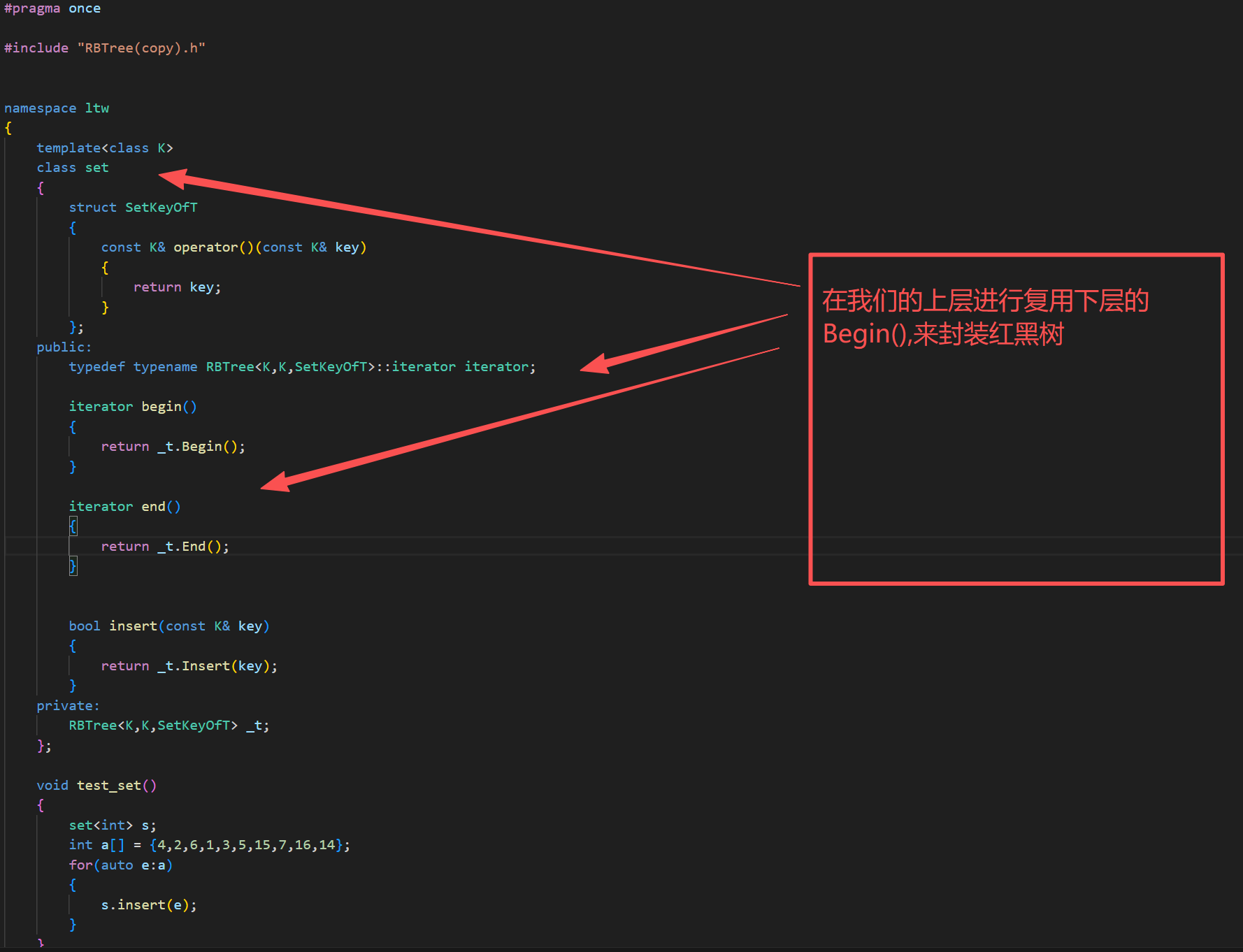
cpp 复制代码 
#pragma once

#include "RBTree(copy).h"


namespace ltw
{
    template<class K>
    class set
    {
        struct SetKeyOfT
        {
            const K& operator()(const K& key)
            {
                return key;
            }
        };
    public:
        typedef typename RBTree<K,K,SetKeyOfT>::iterator iterator;

        iterator begin()
        {
            return _t.Begin();
        }

        iterator end()
        {
            return _t.End();
        }


        bool insert(const K& key)
        {
            return _t.Insert(key);
        }
    private:
        RBTree<K,K,SetKeyOfT> _t;
    };

    void test_set()
    {
        set<int> s;
        int a[] = {4,2,6,1,3,5,15,7,16,14};
        for(auto e:a)
        {
            s.insert(e);
        }
    }
}
cpp 复制代码 
#pragma once

#include "RBTree(copy).h"

namespace ltw
{
    template<class K,class V>
    class map
    {
        struct MapKeyOfT
        {
            const K& operator()(const pair<K,V>& kv)
            {
                return kv.first;
            }
        };
    public:
        typedef typename RBTree<K,pair<K,V>,MapKeyOfT>::iterator iterator;

        iterator begin()
        {
            return _t.Begin();
        }

        iterator end()
        {
            return _t.End();
        }

        bool insert(const pair<K,V>& kv)
        {
            return _t.Insert(kv);
        }
    private:
        RBTree<K,pair<K,V>,MapKeyOfT> _t;
    };
}

3.operator++的重载

我们想一想,红黑树的迭代器进行++,是如何进行++的?

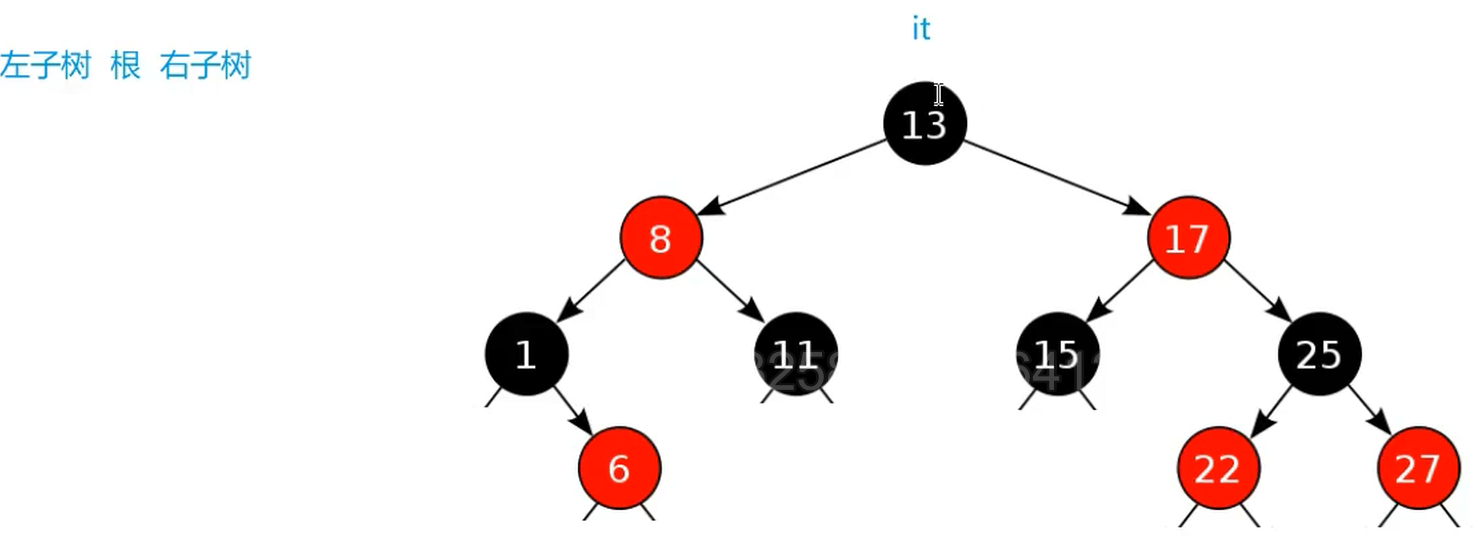
++本质上是在进行中序遍历

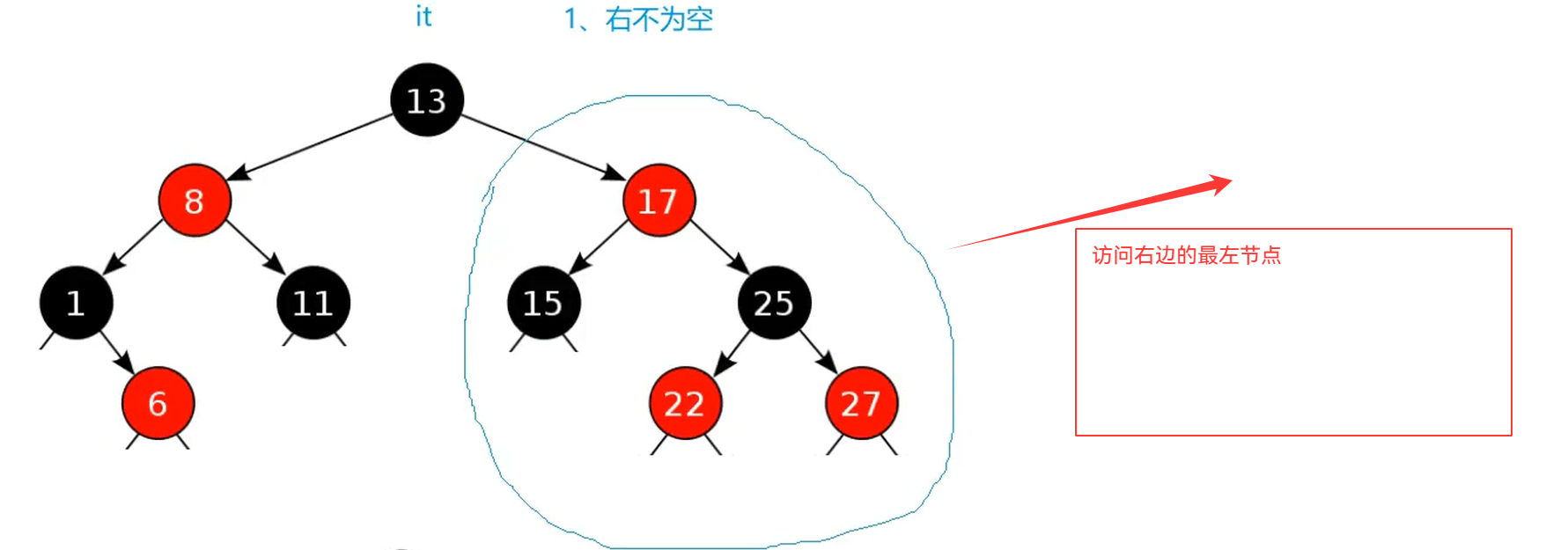
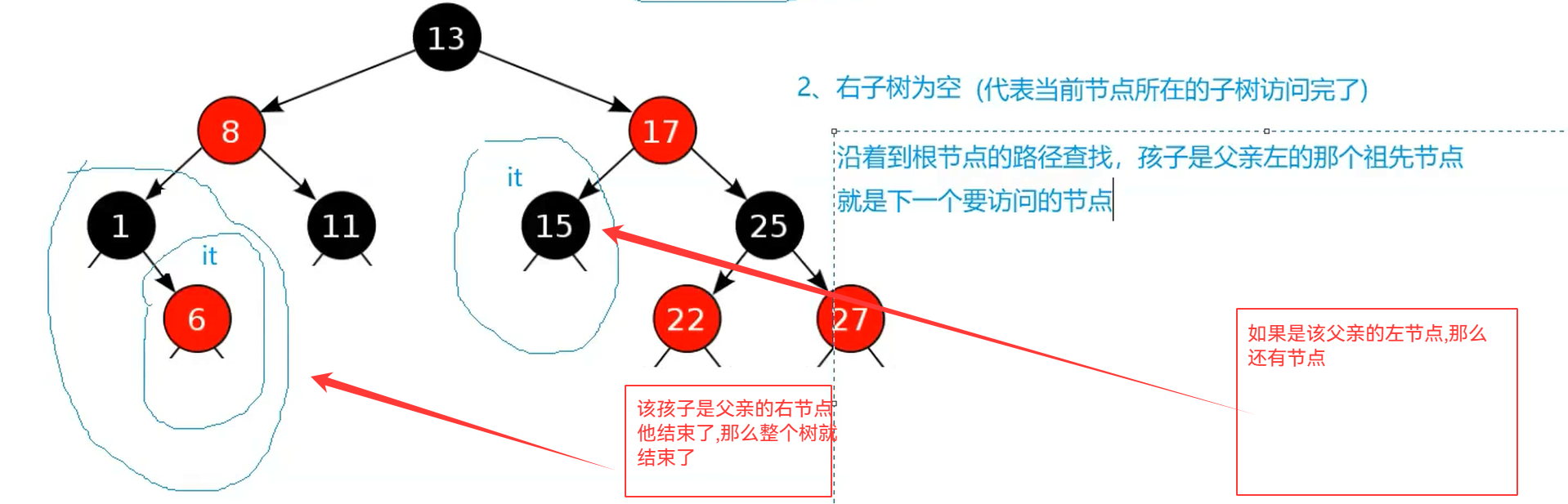
cpp 复制代码 
Self& operator++()
	{
		if(_node->_right)
		{
			//右不为空,右子树最左节点就是中序的下一个
			Node* leftMost = _node->_right;
			while(leftMost&&leftMost->_left)
			{
				leftMost = leftMost->_left;
			}
			_node = leftMost;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while(parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
		return *this;
	}

这个地方我们的_parent提供了遍历

4.begin()和end()的实现

为了实现范围for,我们还要提供我们的begin()和end()

因为begin()本质上是在找我们中序遍历的第一个,就是最左节点

cpp 复制代码 
Iterator Begin()
	{
		Node* leftMost = _root;
		while(leftMost && leftMost->_left)
		{
			leftMost = leftMost->_left;
		}
		return Iterator(leftMost);
	}

end()的实现:

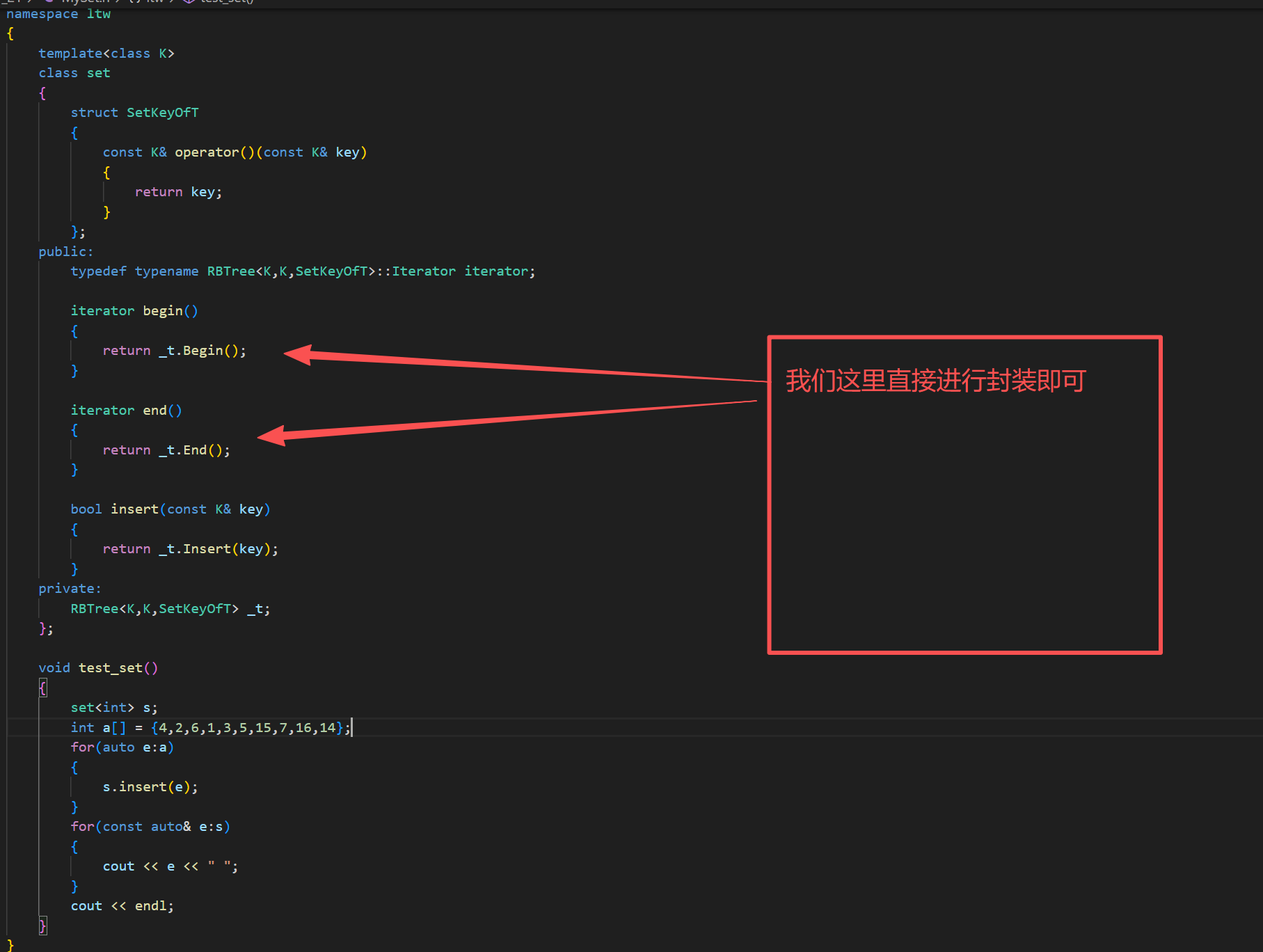
这里能跑很明显就能看到是中序遍历,符合我们二叉树的性质

cpp 复制代码 
void test_map()
    {
        map<int,int> s;
        int a[] = {4,2,6,1,3,5,15,7,16,14};
        for(auto e:a)
        {
            s.insert({e,e});
        }
        for(const auto& e:s)
        {
            cout << e.first << " " << e.second << endl;
        }
        cout << endl;
    }

我们看源码这个地方,是增加了一个哨兵位的头节点

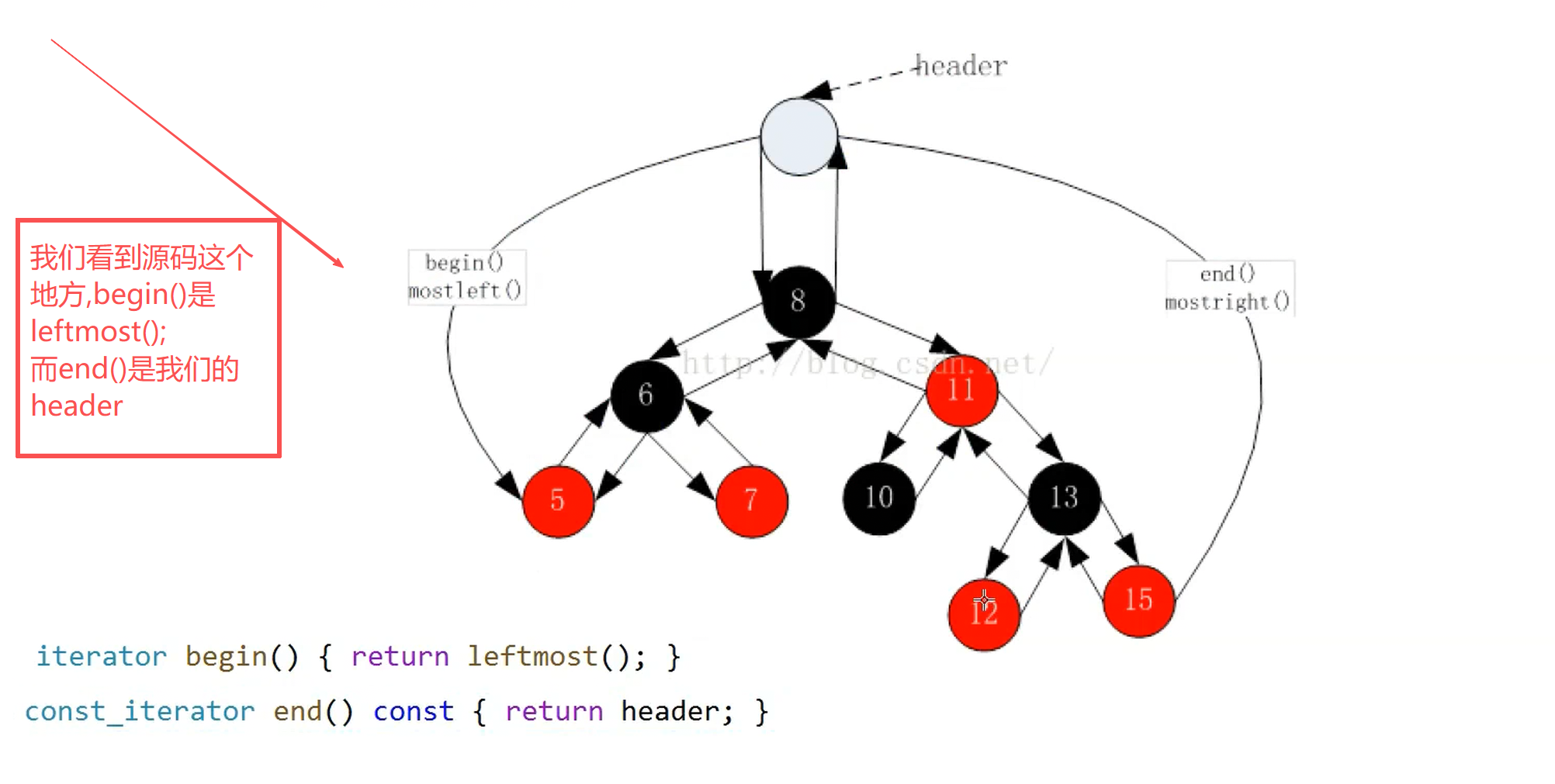
这里设计的header的好处是,header和root是互为父子的,这样判断end()的时候,会更加方便

而且,支持反向迭代器更合理一点

5.operator--的实现

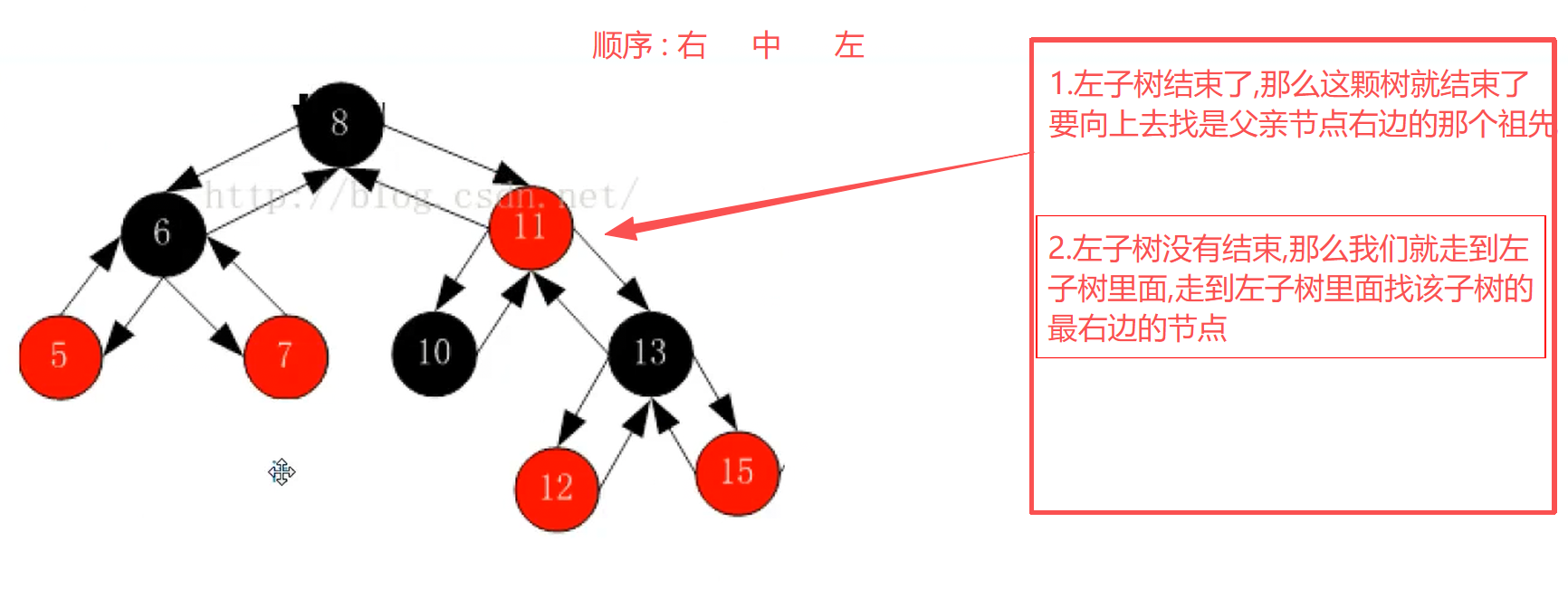
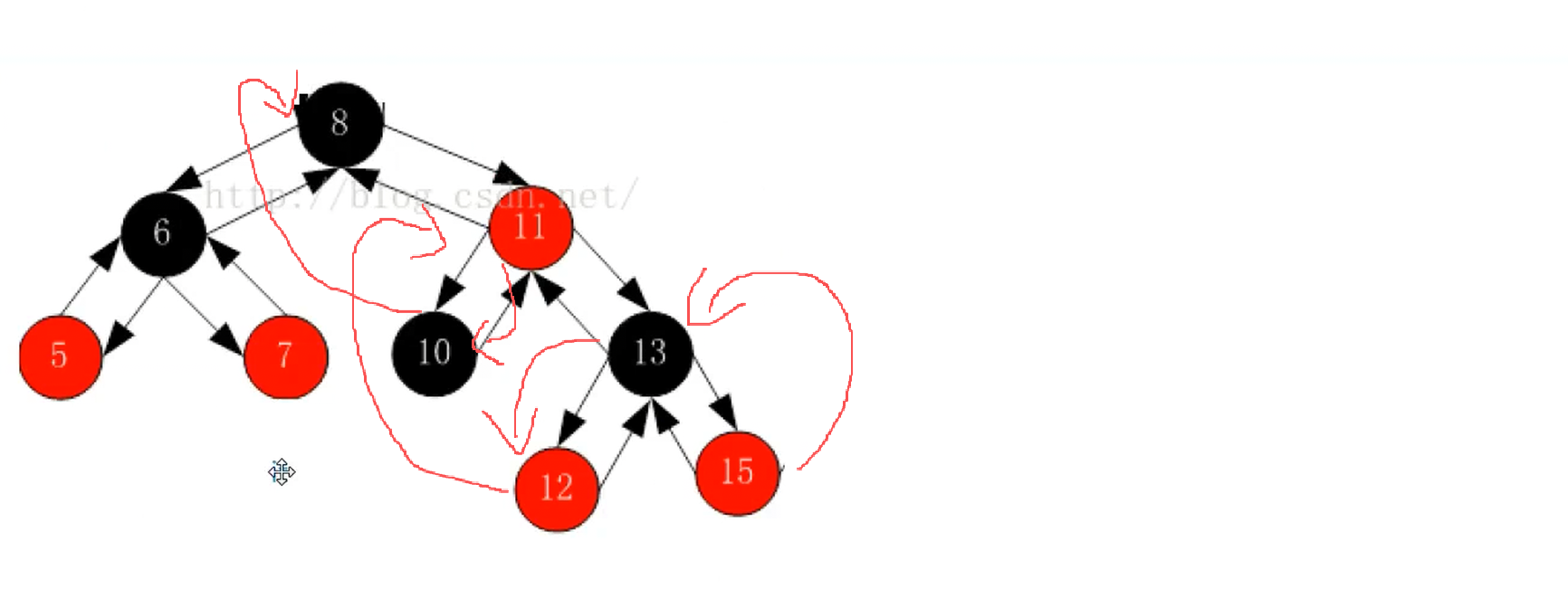
cpp 复制代码 
operator--  代码实现

Self& operator--()
    {
        if(_node->_left)
		{
			Node* rightMost = _node->_left;
			while(rightMost&&rightMost->_right)
			{
				rightMost = rightMost->_right;
			}
			_node = rightMost;
		}
		else
		{
            //找孩子是父亲右边的那个
			Node* cur = _node;
			Node* parent = cur->_parent;
			while(parent && cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
        return *this;
    }

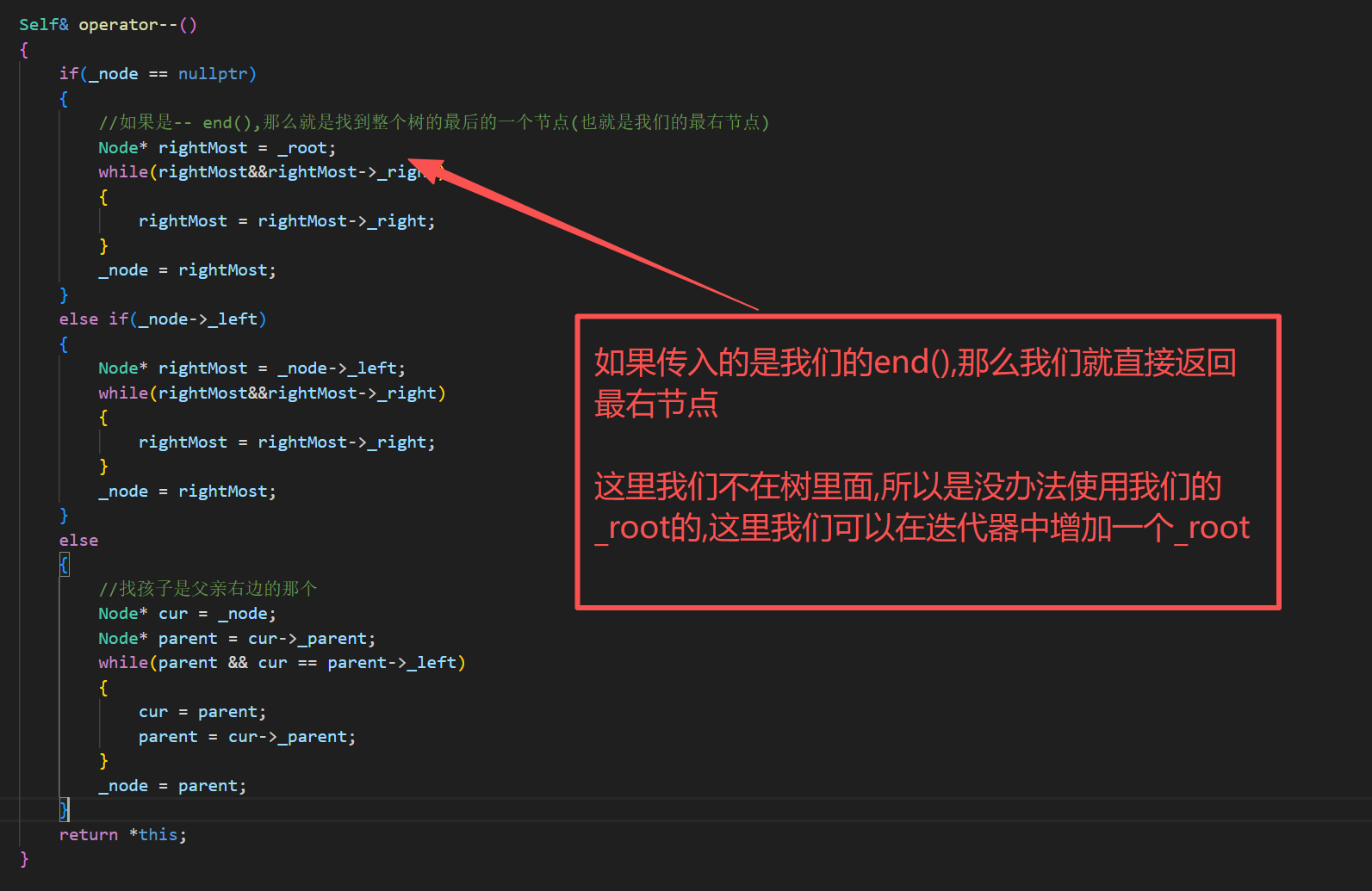
但是我们这里的如果是end() (nullptr)传入--,那么就直接奔溃了,所以我们就要做特殊处理

cpp 复制代码 
Self& operator--()
    {
        if(_node == nullptr)
        {
            //如果是-- end(),那么就是找到整个树的最后的一个节点(也就是我们的最右节点)
            Node* rightMost = _root;
			while(rightMost&&rightMost->_right)
			{
				rightMost = rightMost->_right;
			}
            _node = rightMost;
        }
        else if(_node->_left)
		{
			Node* rightMost = _node->_left;
			while(rightMost&&rightMost->_right)
			{
				rightMost = rightMost->_right;
			}
			_node = rightMost;
		}
		else
		{
            //找孩子是父亲右边的那个
			Node* cur = _node;
			Node* parent = cur->_parent;
			while(parent && cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}
        return *this;
    }

但是,这样实现还是有缺陷的,这样会面临迭代器失效(这块是一个大坑),这里我们可以采取库里面的方式设计

我们这样也能实现set的反向遍历

cpp 复制代码 
set<int>::iterator it = s.end();
        while(it != s.begin())
        {
            --it;
            cout << *it << " ";
        }
        cout << endl;

这里再讲一下我们的迭代器优势(迭代器模式):

6.const迭代器的实现

这里加const迭代器,我们采用的是以前链表的实现方式,代码链接如下:

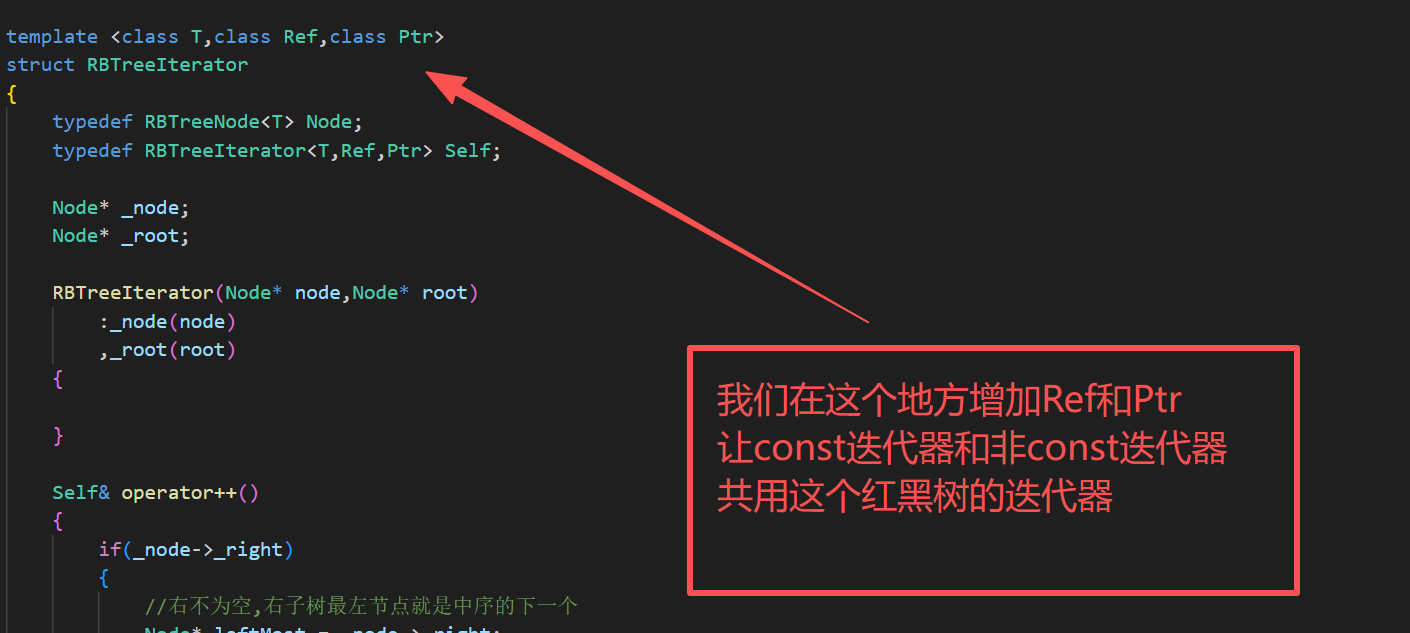
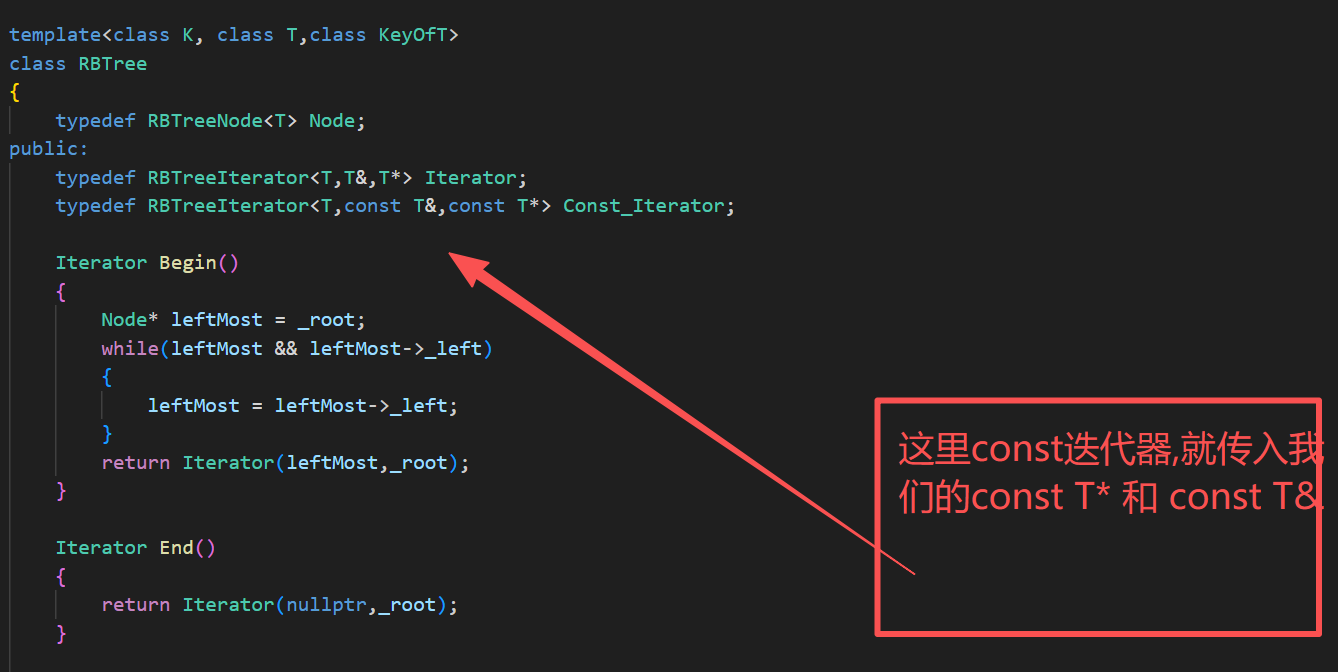
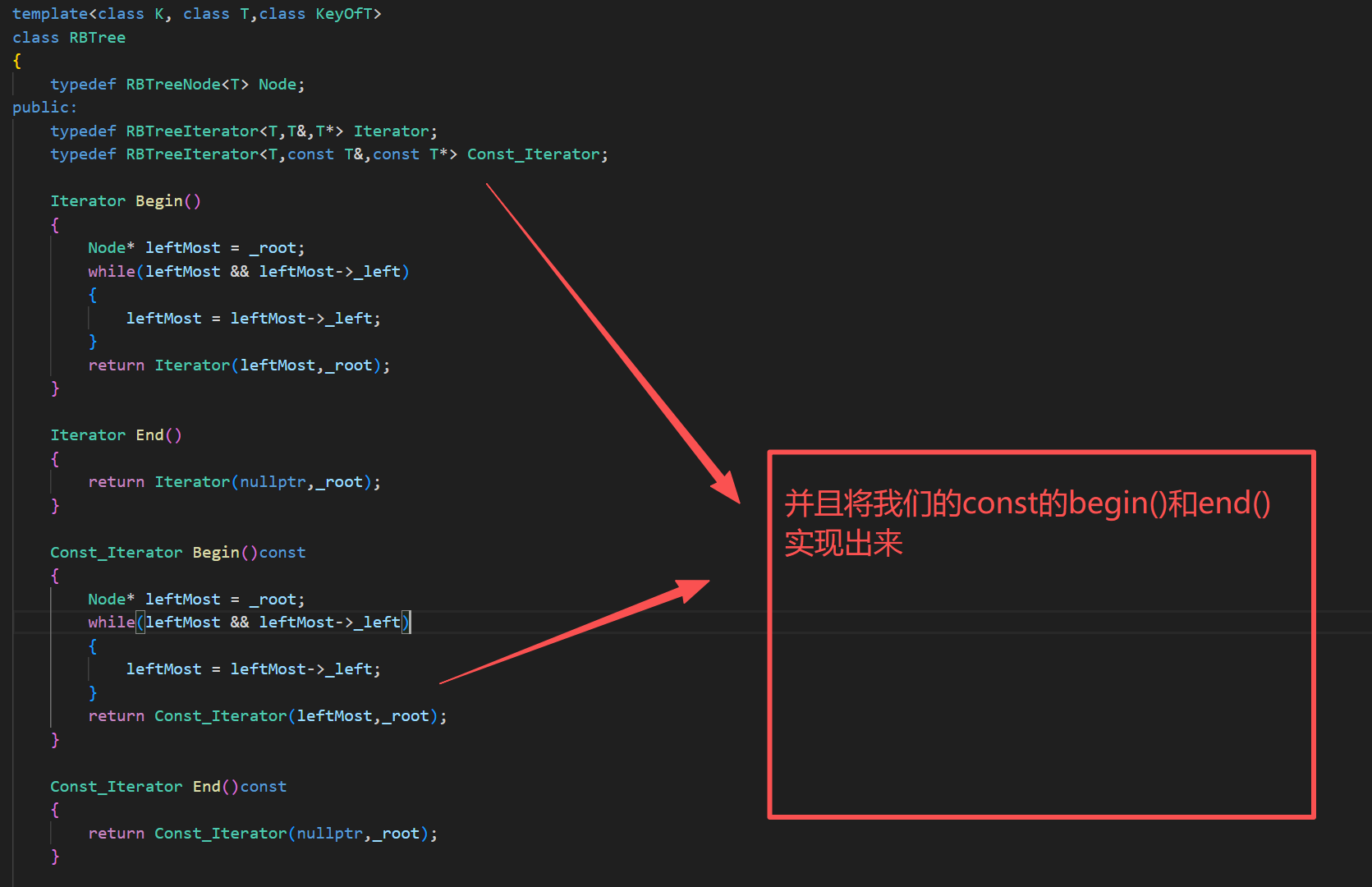
https://blog.csdn.net/weixin_60668256/article/details/153393453?fromshare=blogdetail&sharetype=blogdetail&sharerId=153393453&sharerefer=PC&sharesource=weixin_60668256&sharefrom=from_link

测试代码:

cpp 复制代码 
void Print(const set<int>& s)
    {
        set<int>::const_iterator it = s.end();
        while(it != s.begin())
        {
            --it;
            cout << *it << " ";
        }
    }

    void test_set()
    {
        set<int> s;
        int a[] = {4,2,6,1,3,5,15,7,16,14};
        for(auto e:a)
        {
            s.insert(e);
        }
        for(const auto& e:s)
        {
            cout << e << " ";
        }
        cout << endl;
        set<int>::iterator it = s.end();
        while(it != s.begin())
        {
            --it;
            cout << *it << " ";
        }
        cout << endl;
        Print(s);
    }

毕竟是树形的结构,如果改变一个节点的值就不一定是搜索树了

,还有一点,就是map的first是不支持修改的,但是map的second是支持修改的,所以我们在这个代码不能直接使用const迭代器

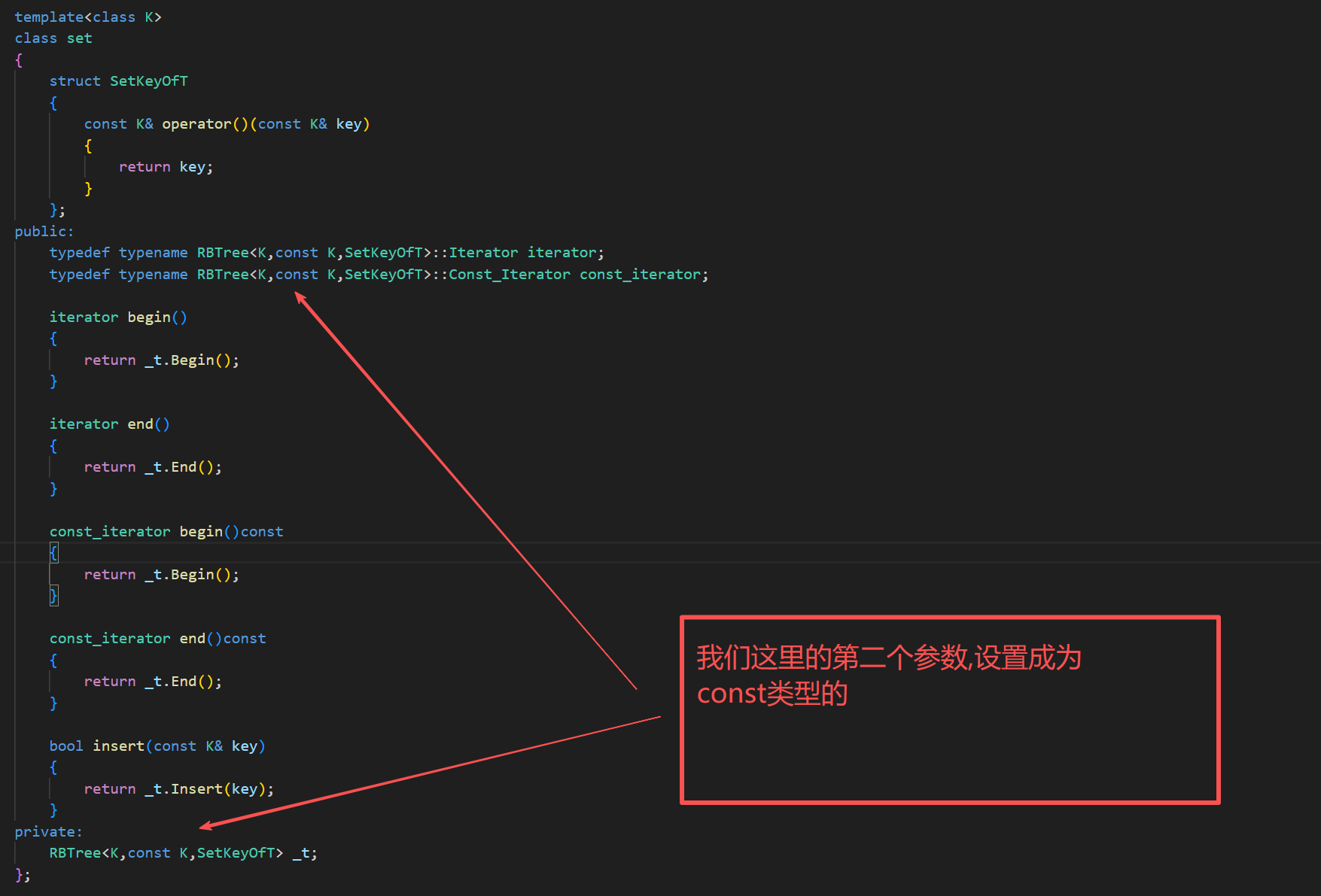
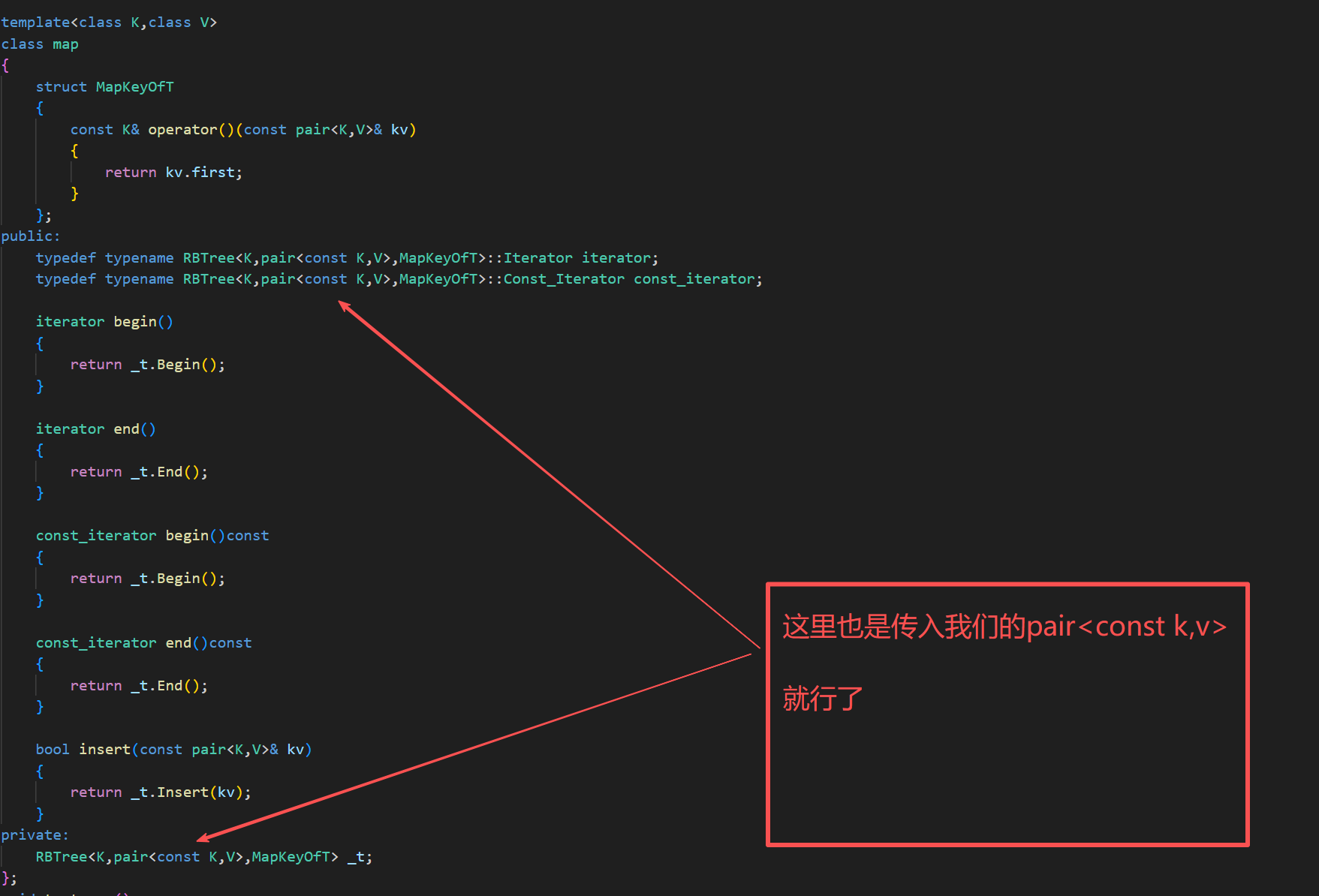
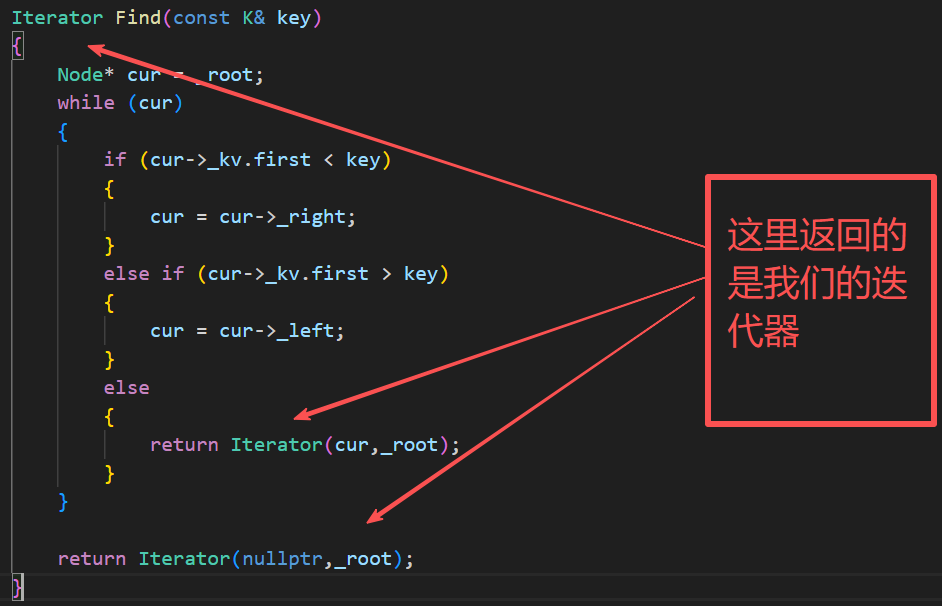
7.Find的实现

cpp 复制代码 
Iterator Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				cur = cur->_right;
			}
			else if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else
			{
				return Iterator(cur,_root);
			}
		}

		return Iterator(nullptr,_root);
	}

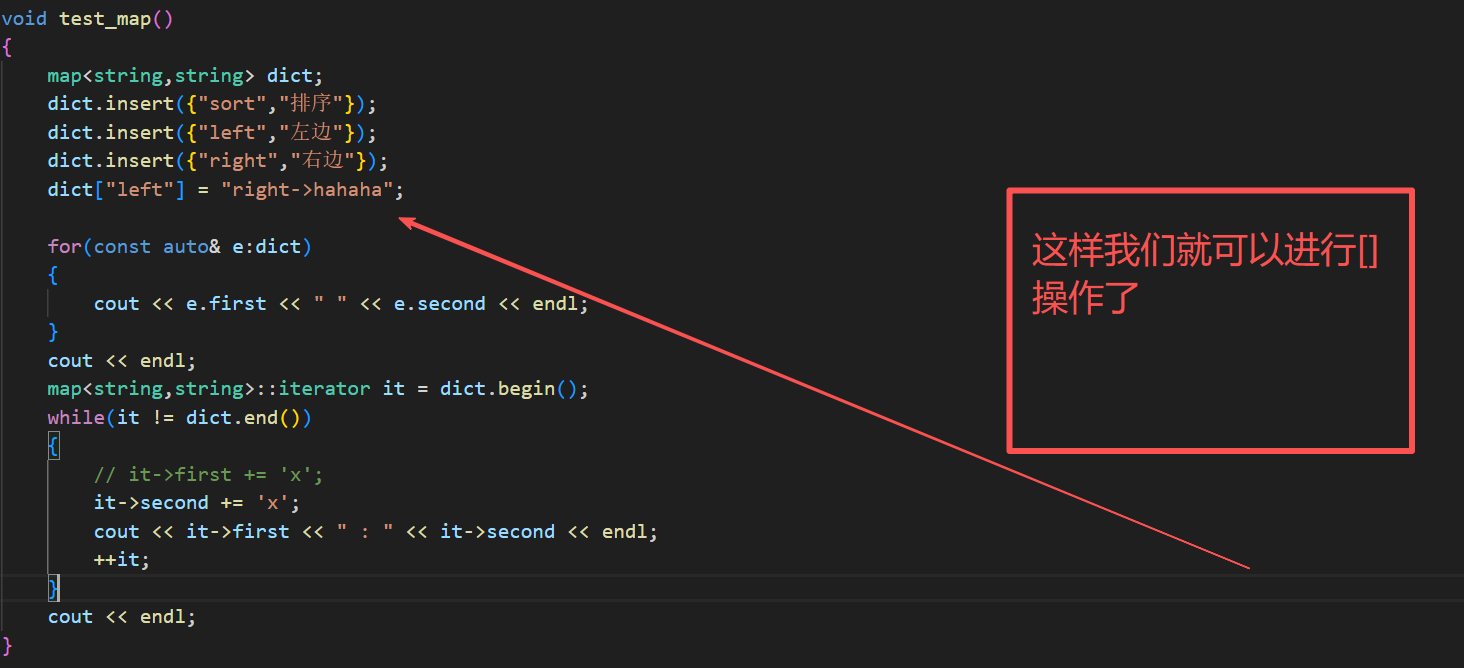
8.map实现我们的operator[]

map的[]实现,应该依赖我们的insert

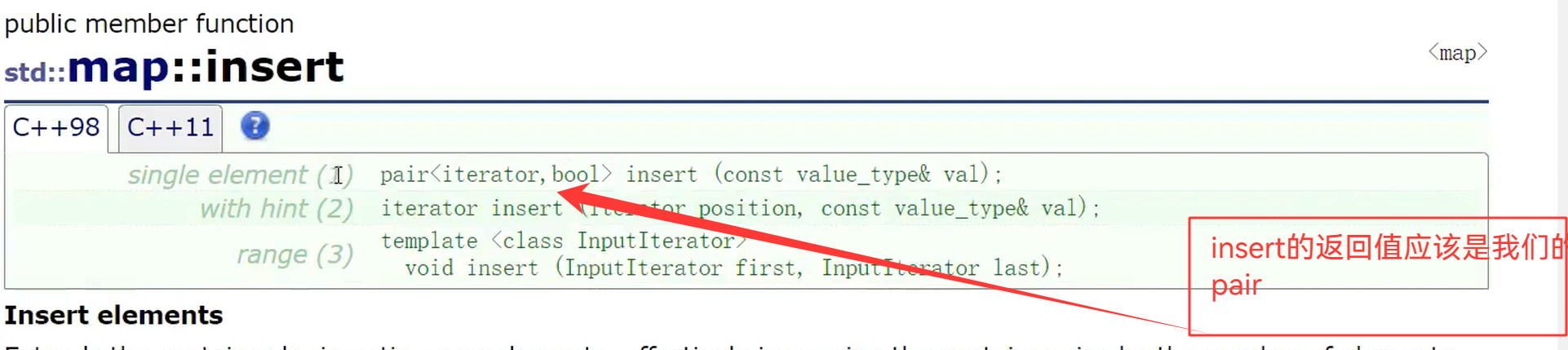
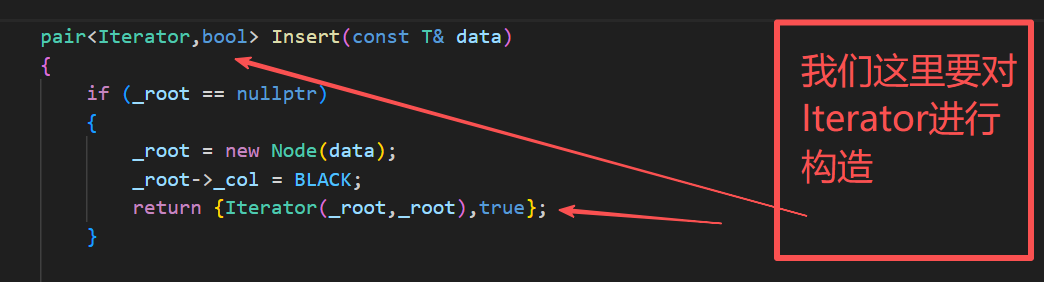
所以,我们要进行修改插入函数

cpp 复制代码 
pair<Iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return {Iterator(_root,_root),true};
		}

		KeyOfT kot;

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return {Iterator(cur,_root),false};
			}
		}

		cur = new Node(data);
		Node* newnode = cur;
		// 新增节点。颜色红色给红色
		cur->_col = RED;
		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		cur->_parent = parent;

        while(parent && parent->_col == RED)
        {
            Node* grandfather = parent->_parent;
            if(parent == grandfather->_left)
            {
                //       g
                //   p       u
                Node* uncle = grandfather->_right;
                if(uncle && uncle->_col == RED)
                {
                    //叔叔存在且为红  -> 变色+向上处理
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;
                }
                else
                {
                    //叔叔存在且为黑/不存在  -> 变色+向上处理
                    if(cur == parent->_left)
                    {
                        //     g
                        //   p    u
                        // c
                        // 单旋
                        RotateR(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    else
                    {
                        //      g
                        //   p     u
                        //     c
                        //双旋
                        RotateL(parent);
                        RotateR(grandfather);
                        cur->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    break;
                }
            }
            else
            {
                //       g
                //   u       p
                Node* uncle = grandfather->_left;
                if(uncle && uncle->_col == RED)
                {
                    //叔叔存在且为红  -> 变色+向上处理
                    parent->_col = uncle->_col = BLACK;
                    grandfather->_col = RED;

                    cur = grandfather;
                    parent = cur->_parent;
                }
                else
                {
                    //叔叔存在且为黑/不存在  -> 变色+向上处理
                    if(cur == parent->_right)
                    {
                        //     g
                        //   u    p
                        //           c
                        // 单旋
                        RotateL(grandfather);
                        parent->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    else
                    {
                        //      g
                        //   u     p
                        //       c
                        //双旋
                        RotateR(parent);
                        RotateL(grandfather);
                        cur->_col = BLACK;
                        grandfather->_col = RED;
                    }
                    break;
                }
            }
        }
        _root->_col = BLACK;

		return {Iterator(newnode,_root),true};
	}
cpp 复制代码 
V& operator[](const K& key)
        {
            pair<iterator,bool> ret = insert({key,V()});
            return ret.first->second;
        }
相关推荐
孤廖3 小时前
C++ 模板再升级：非类型参数、特化技巧（含全特化与偏特化）、分离编译破解
linux·服务器·开发语言·c++·人工智能·后端·深度学习
水冗水孚3 小时前
双指针算法在实际开发中的具体应用之代码Review文章字符串的片段分割
算法·leetcode
DuHz3 小时前
用于汽车雷达应用的步进频率PMCW波形——论文阅读
论文阅读·算法·汽车·信息与通信·信号处理·毫米波雷达
润 下3 小时前
C语言——回调函数的典型示例（分析详解）
c语言·开发语言·人工智能·经验分享·笔记·程序人生
朝新_3 小时前
【EE初阶 - 网络原理】传输层协议
java·开发语言·网络·笔记·javaee
张晓～183399481213 小时前
碰一碰发抖音源码技术搭建部署方案
线性代数·算法·microsoft·矩阵·html5
weixin_448119943 小时前
Datawhale人工智能的数学基础 202510第3次作业
人工智能·算法
前端架构师-老李3 小时前
Java开发—JDK的安装和版本管理（macOS）
java·开发语言·macos
田野追逐星光3 小时前
STL中容器string -- 讲解超详细
c++
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04Linux下V2Ray安装配置指南05GitLab 零基础入门指南：从安装到项目管理全流程06XXE 注入漏洞全解析：从原理到实战07NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）092025软件测试面试八股文（含答案+文档）10两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答