摘要。
飞行时间(ToF)传感器越来越多地用于移动设备进行深度传感。然而，噪声的存在，如多路径干扰(MPI)和散粒噪声，降低了ToF成像质量。以前的基于cnn的方法在不考虑场景空间层次结构的情况下去除ToF深度噪声，导致在复杂场景中获得高质量的深度图像失败。在本文中，我们提出了一种空间层次感知残差金字塔网络，称为SHARP-Net，通过充分利用不同尺度的场景几何信息来去除深度噪声。SHARP-Net首先引入了一个残差回归模块，该模块利用深度图像和振幅图像作为输入，逐步计算深度残差。然后，导入残差融合模块，对来自所有尺度的深度残差求和，通过融合多尺度几何信息来细化深度残差。最后，核预测网络进一步消除了散粒噪声。实验结果表明，我们的方法在合成数据集和真实数据集上明显优于最先进的ToF深度去噪方法。源代码可在 https://github.com/ashesknight/tof-mpi-remove 获得。
1 Introduction
Depth在当前的研究中扮演着重要的角色，特别是在计算机视觉领域。在过去的几十年里，研究人员提出了各种方法来获得深度[30,29,22]，其中飞行时间(ToF)技术在深度传感方面变得越来越流行。许多成功的消费产品，如Kinect One[21]，都配备了ToF传感器，提供高质量的深度图像。这些设备进一步促进了计算机视觉领域的许多应用，例如场景理解、动作识别和人机交互。然而，ToF深度图像受到多径干扰(MPI)和散粒噪声等各种噪声的影响，这限制了ToF成像技术的适用性。
图1所示。(a)ToF振幅图像。(b) ToF 地面实况深度。(c) 散粒噪声引起的深度误差图。(d) MPI 引起的深度误差图。该示例来自合成数据集
ToF深度图像容易受到MPI噪声的影响，这是由于曝光过程中一个像素收集了大量的多反射光时间。MPI的存在打破了接收光只在场景中反射一次的关键假设，导致严重的ToF深度误差。镜头噪声是传感器电子引起的常见且不可避免的噪声，是ToF深度噪声的另一个来源。图 1 显示了分别由散粒噪声和 MPI 噪声引起的深度误差图。可以看出，在ToF深度图像中，镜头噪声和MPI噪声都很普遍，但在角落和边缘区域等多个区域，MPI噪声显著强烈
最近，许多基于卷积神经网络(CNN)的方法被提出用于ToF传感器的MPI去除[17,23,26]。这些基于 CNN 的方法的基本理论是像素的 MPI 噪声可以估计为来自周围像素的信息的线性组合 。在图像空间中，CNN 是一种将这种线性组合过程与空间卷积建模的合适方法，并取得了令人鼓舞的结果。为了拟合卷积核的未知参数，经常使用监督学习，不需要MPI场景的地真标签。由于很难获得真实场景的基本事实深度，因此引入了许多合成ToF数据集来训练和测试神经网络。通常，这些数据集由ToF深度图像和相应的振幅图像 组成。一些数据集甚至包含ToF传感器和彩色图像的原始测量值，这两个数据集通常由校准的RGBD相机捕获。
大规模数据集使得通过基于 CNN 的方法学习光传输的线性组合过程成为可能。然而，现有的基于 CNN 的方法仍然存在一些局限性。特别是，消除复杂场景的MPI噪声并不令人满意。具体来说，在复杂场景中，许多不同形状和大小的物体彼此靠近。在这种情况下，ToF 传感器的每个像素可能会收集许多来自各种间接光路的光信号，这很容易导致强烈的 MPI 噪声。在复杂场景中消除MPI噪声仍然是一个具有挑战性的问题，需要更多的研究。
一个关键的观察结果是，在场景中，对象通常具有空间层次结构。例如，展示、狗玩具和狗玩具的头部可以制定层次关系。在这种情况下，位于任何物体表面的点的深度值通常受到这三个相互关联的对象的影响。在形状大、结构详细的复杂场景中应该有更多样化的层次关系。以往的研究表明，利用场景的层次表示可以提高计算机视觉领域的改进，如场景理解[24,27]、图像嵌入[4]、图像去噪[20]、目标检测[19]、深度和三维形状估计[6,18]。上述工作启发我们明确地利用空间层次关系来提高ToF深度MPI去除的结果。
在本文中，我们提出了一种空间层次感知残差金字塔网络(SHARP-Net)，以充分利用多尺度的场景结构进行ToF深度去噪。场景的空间层次结构，以多尺度特征金字塔的形式，可以为网络提供适当的接受域和更充足的场景对象之间的关系，提高了噪声去除的性能。
在SHARP-Net中，首先引入了一个残差回归模块，该模块由一个特征提取器组成，构建一个特征金字塔和残差回归块，以粗到细的方式建立深度残差金字塔。在残差金字塔的上层，深度残差图表示利用全局几何信息回归的MPI噪声。在较低的层次上，深度残差图通过考虑局部场景结构来描述细微的MPI效应。残差回归模块推动每个级别利用当前级别的可用层次关系，并深入提取位于场景相应层次中的几何信息。不同尺度获得的几何信息为估计MPI噪声提供了极好的提示。我们提出的残差回归模块为每个级别生成一个深度残差图，这与广泛使用的 U-Net 结构有很大不同。在经过残差回归模块后，得到深度残差金字塔来表示与场景的层次结构相对应的MPI估计。为了进一步优化SHARP-Net在大尺寸形状和详细结构上的性能，我们提出了一种残差融合模块，通过对来自所有尺度的深度残差求和来显式选择主要分量。最后，我们采用了一种基于深度细化模块，该模块基于核预测网络，去除镜头噪声和细化深度图像。
-我们提出了一个残差回归模块，显式地利用场景的空间层次结构，以同时准确地去除大尺寸形状和详细结构中的MPI噪声和镜头噪声。
-我们提出了一个残差融合模块，有选择地集成不同尺度的几何信息，以进一步纠正MPI噪声，并引入深度细化模块来有效地消除镜头噪声。
-所提出的SHARP-Net在合成数据集和真实数据集上的ToF深度去噪的定量和定性比较方面明显优于最先进的方法。
2 相关工作
ToF 成像受到来自不同来源的噪声的影响，例如散粒噪声和 MPI 噪声 [15, 28]。镜头噪声是由传感器电子设备引起的，该传感器电子设备出现在所有传感器中。对ToF传感器的镜头噪声去除得到了很好的研究。传统的滤波算法，如双边滤波，能够有效地消除散粒噪声[2,16]。相比之下，MPI去除是ToF深度去噪中更困难的问题。已经提出了许多基于物理的和基于学习的MPI去除方法。
对于基于物理的方法，Fuchs 等人。进行了一系列研究来估计场景中的 MPI 噪声，从单个调制频率 [9] 来考虑多个反照率和反射 [10, 14]。Feigin等人通过比较不同频率的原始测量的像素级变化，提出了一种多频率方法来校正MPI[5]。Gupta等人研究了调制频率对MPI的影响，提出了一种相量成像方法，通过发射两个频率差异较大的信号[12]。Freedman等人提出了一种基于可压缩后向散射表示的模型，利用两条路径处理多路径，实现实时处理速度[8]。
对于基于学习的方法，Marco 等人。利用瞬态成像技术 [13] 来模拟 TToF 成像过程中 MPI 噪声的生成，并为 TToF 深度去噪生成大型数据集。他们还提出了一个两阶段的深度神经网络来细化ToF深度图像[17]。Su等人提出了一种用于ToF深度去噪的深度端到端网络，该网络以原始相关测量作为输入[26]。郭等人。生成一个大规模的ToF数据集FLAT，并引入核预测网络来去除MPI和散粒噪声[11]。为了克服未标记现实场景和合成训练数据集之间的域转移，Agresti等人利用基于生成对抗网络的对抗学习策略，从合成数据集到真实场景[2]执行无监督域适应。邱等人。考虑了 RGB-D 相机提供的相应 RGB 图像，并提出了一个用于相机对齐的深度端到端网络和 ToF 深度细化 [23]
最近，残差金字塔方法已被用于各种计算机视觉任务。对于立体匹配，Song 等人。构建一个残差金字塔来解决困难区域深度图像的退化，例如非纹理区域、边界区域和微小细节[25]。对于单目深度估计，Chen等人提出了一种结构感知残差金字塔，以粗到细的方式恢复视觉质量高的深度图像[6]。对于图像分割，Chen等人提出了一种残差金字塔网络来学习不同尺度[7]中的主要和残差分割。对于图像超分辨率，Zhenget 等人。采用联合残差金字塔网络来有效地扩大感受野 [31]。我们的SHARP-Net也指残差金字塔方法，以及在ToF深度去噪方面取得了成功，这将在以下部分中详细解释。据我们所知，SHARP-Net 是第一个将残差金字塔应用于 ToF 深度去噪的工作，它通过集成空间层次结构大大超越了现有方法。
3ToF成像模型
在本节中，我们将简要介绍ToF成像和MPI的数学模型。使用单个调制频率 fω 和四步相移测量 ri (i = 1, 2, 3, 4)，每个像素处的深度 d 计算为
其中 P 是所有光路 p 的集合，然后是间接接收信号。这里间接接收到的信号 sp(t) 表示在向场景发射后反射多次反弹的捕获信号。s(t) 和 ^s(t) 之间的差异进一步导致深度 d 的偏差。在我们提出的网络中，我们称之为深度残差的偏差。为了更好地回归深度残差，我们在残差金字塔中引入一个残差金字塔来估计多尺度的MPI噪声。在金字塔的不同层次上，集合 P 引起的偏差被我们的网络回归并进一步优化。
4空间层次感知残差金字塔网络
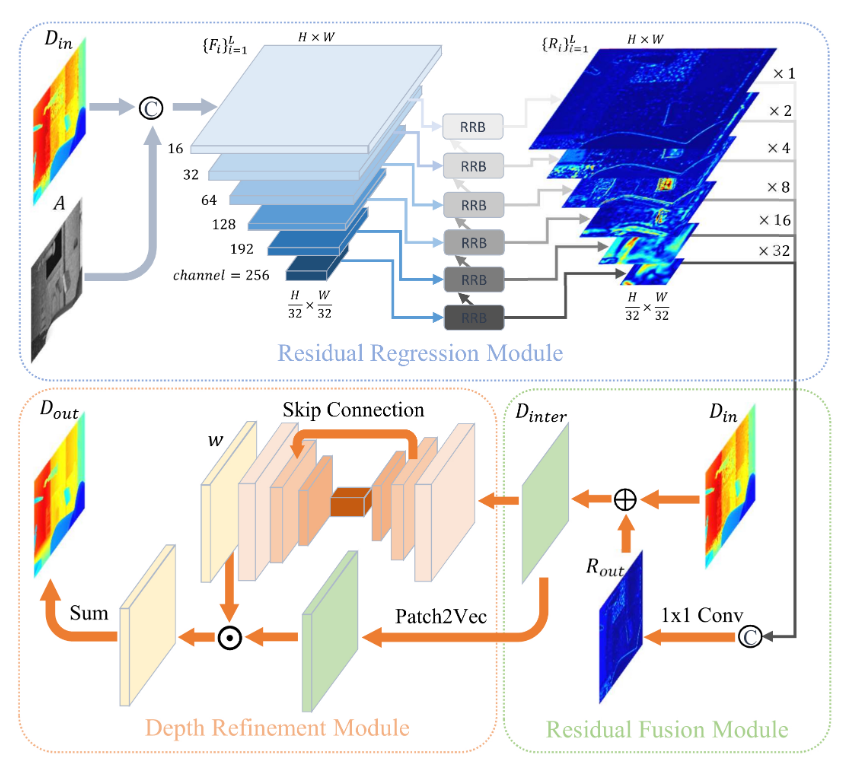图 2. 空间层次感知残差金字塔网络 (SHARPNet) 流程图。这里⊙表示点积运算，©是连接操作，⊕表示加法运算。'Patch2Vec' 表示将每个像素的邻域重塑为向量的操作。
我们提出的空间层次感知残差金字塔网络(SHARPNet)由三部分组成:残差回归模块作为多尺度特征提取的骨干、残差融合模块和深度细化模块来优化性能。SHARP-Net的流程图如图2所示。以下小节分别解释这三个部分。
4.1残差回归模块
作为SHARP-Net的主干，残差回归模块首先引入特征编码器，从深度图像Din和振幅图像A的组合中提取多尺度特征金字塔{Fi}L i=1，其中Fi表示第i层提取的特征图，L为金字塔中的层数。当输入图像的大小为 W × H 时，第 i 层的特征图大小为 W2i−1 × H2i−1 × Ci，其中 Ci 是输出通道的数量。在我们的网络中，我们设置 L = 6 以保持参数数量与最先进方法相似。对应的Ci分别为16、32、64、128、192、256。从底部到顶部，特征金字塔逐渐编码了场景中更详细的结构的几何信息。在每个层次上，提出了一种残差回归块，如图3所示，用于预测深度残差图。通过双三次插值将较低级别的 Ri+1 的深度残差图上采样 2 倍，然后与当前级别的特征图连接。新的连接体积是五个顺序卷积层的输入，它输出当前级别的残差 mapRi。具体来说，对于底层，残差回归块的输入只是大小为W32 × H32 × 256的特征图，因为有没有来自较低级别的深度残差图。与之前通过顺序上采样特征图直接回归残差图的方法不同，我们的残差回归模块通过考虑场景的层次结构，以粗到细的方式逐步回归多尺度残差图。低分辨率的残差图描绘了大尺寸形状中存在的深度噪声，而更高分辨率的残差图侧重于详细结构中存在的深度噪声。最后，我们得到一个残差金字塔 {Ri}L i=1，由每个级别的深度残差图组成。
4.2残差融合模块
残差金字塔的最上层提供了原始分辨率的深度残差图，可以看作是对深度误差的估计。然而，来自单个级别的深度残差图不能充分利用场景的几何信息。尽管残差金字塔的最上层包含来自下面所有级别的信息，但在卷积操作之后，来自较低分辨率级别的信息可能会丢失。因此，我们提出了一个残差融合模块来显式地组合所有尺度上的深度残差映射。首先通过双三次插值将每个级别的深度残差图上采样到原始分辨率。然后将所有上采样的深度残差图连接在一起。新的残差体积是1×1卷积层的输入。在卷积操作之后，我们得到最终的深度残差图 Rout。将深度残差图添加到原始输入深度图像中，深度图像恢复为Dinter。剩余融合模块的细节如图2所示。
4.3深度细化模块
在前两个模块之后，在很大程度上去除了MPI噪声。同时，散粒噪声也得到了缓解，但不如MPI去除。散粒噪声的存在仍然阻碍了ToF深度传感的应用。为了解决这个问题，我们提出了一个深度细化模块，该模块利用核预测网络[3]进一步去除镜头噪声。
深度细化模块以中间深度图像Dinter为输入，采用跳跃式连接的U-Net模型生成权重矩阵。权重矩阵由深度图像中每个像素的矢量化滤波器核组成。在我们的实验中，我们将内核大小 k 设置为 3，权重矩阵的大小为 W × H × 9。接下来，我们通过为深度图像中的每个像素向量化邻域来生成补丁矩阵。我们将上述操作称为"Patch2Vec"。当邻域为3×3区域时，很容易计算面片矩阵的大小也是W×H×9。然后将权重矩阵与面片矩阵逐个元素相乘，生成相同大小的3D体积。通过对3D体积求和，最终得到细化后的深度图像Dout。图 2 还显示了深度细化模块的细节。
4.4损失函数
为了训练我们提出的SHARP-Net中的参数，我们需要计算预测深度图像Dout与相应地面真实深度图像Dgt之间的差异。损失函数应该引导我们的网络在保持几何细节的同时准确地去除深度噪声。在[23]之后，我们的损失函数有两个分量，分别是L1损失和它在精化深度图像上的梯度。损失函数的公式描述为
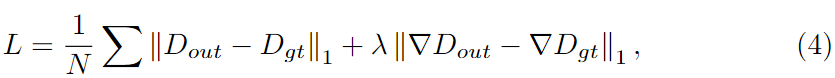
其中‖·‖1表示L1范数，N为像素数。这里使用离散Sobel算子来计算梯度。在我们的实验中，我们设置 λ = 10
5 实验
5.1数据集
我们的SHARP-Net是一个有监督的神经网络，用于去除ToF深度图像的噪声。为了训练所有参数，我们需要具有地面真实深度的ToF数据集。为了生成合适的数据集，主流方法是在引入MPI和镜头噪声[13]的同时，应用瞬态渲染技术来模拟ToF成像过程。以前的基于 CNN 的 ToF 去噪方法提供了几个具有数千个场景的合成数据集。在我们的实验中，我们选择了两个大规模的合成数据集ToF-FlyingThings3D (TFT3D)[23]和FLAT[11]进行训练和评估。TFT3D数据集包含6250个不同的场景，如客厅和浴室。我们只使用分辨率为640 × 480的ToF振幅图像和ToF深度图像作为我们提出的方法的输入。FLAT 数据集总共提供了 1929 个场景，其中包括原始测量值和相应的地面实况深度。通过使用FLAT数据集发布的管道，我们将原始测量值转换为ToF深度图像和分辨率为ToF振幅图像424 × 512。此外，为了评估SHARP-Net在现实场景中的性能，我们还采用了Agresti等人在[2]中构建的True Box数据集。True Box 数据集的地面实况深度由与 ToF 传感器联合校准的活动立体系统获得。总共有 48 个不同的场景，数据集上分辨率为 239 × 320。
5.2数据预处理
我们根据数据集提供的深度值范围对输入深度图像进行归一化，过滤掉深度值不在(0,1)范围内的像素。为了便于实验，我们将TFT3D数据集和FLAT数据集上的图像裁剪为384 × 512。对于True Box数据集，我们将图像裁剪为224 × 320。此外，对于FLAT数据集，我们按照[23]中的实验设置排除了没有背景的场景。对于所有三个数据集，我们随机选择 20% 的场景作为测试集，其余场景用于训练。
5.3 训练设置
对于 TFT3D 数据集，学习率设置为 4 × 10−4，每 2 个 epoch 后减少 30%。我们训练了 40 个 epoch 的 SHARP-Net，批量大小为 2。对于 FLAT 数据集，我们将学习率设置为 1 × 10−4，并进行速率衰减。我们以 8 的批大小训练 SHARP-Net 100 个 epoch。对于 True Box 数据集，训练设置与 TFT3D 数据集的训练设置一致。该网络是使用 TensorFlow 框架 [1] 实现的，并使用 Adam 优化器进行训练。使用四个 NVIDIA TITAN Xp 显卡，TFT3D 和 FLAT 数据集的训练过程大约需要 20 小时，True Box 数据集的训练过程不到半小时。
5.4消融研究
SHARP-Net是一种基于CNN的方法，具有6级残差回归模块作为骨干，以及两个额外的融合和细化模块。为了验证我们提出的模块的有效性，我们设计了实验来比较SHARP-Net及其变体。
-WOFusRef：没有深度细化模块和剩余融合模块的SHARP-Net变体。
-WORefine：没有深度细化模块的SHARP-Net的变体。
-WOFusion：没有剩余融合模块的SHARP-Net的变体。
-四级：主干有4个级别的SHARP-Net的变体。
-五级：主干有5个级别的SHARP-Net的变体。
为了与 FourLevel 和 FiveLevel 进行公平比较，我们需要确保这两种变体的参数数量与 SARPNet 几乎相同。因此，我们调整了变体的卷积核通道数。
对于定量比较，我们使用两个指标，平均绝对误差 (MAE) 和相对误差来评估性能。原始噪声深度图像和地面真实深度图像之间的MAE被描述为原始MAE。然后，我们将相对误差定义为每种方法的MAE与相应输入的MAE之比。还计算了每个误差级别的整体和部分 MAE/Relative 误差。不同的去噪方法在不同的误差水平下可能具有不同的性能。在我们的实验中，我们采用了一种类似于[23]中方法的评估方法，在不同的误差水平下全面评估我们提出的SHARP-Net。首先，我们计算输入深度图像和ground truth之间的逐像素绝对误差值。然后我们按升序对所有逐像素绝对误差进行排序。接下来，测试集中的所有像素被分成四个分位数（四个错误级别集）。我们的评估方法与 [23] 中的方法的区别在于我们对测试集中的所有像素进行排序，而不是在单个图像中。这种变化使我们的评估更加合理，因为整个测试集中的排序消除了图像的深度区分。0%-25% 范围内的像素被分类为第一个错误级别。同样，25%-50% 和 50%-75% 和 75%-100% 范围内的像素被分类为第 2、第 3 和第 4 个错误级别。这里将深度值超过每个数据集的最大深度的像素视为异常值，并从任何错误级别集中排除。最后，我们分别计算了不同误差级别的部分 MAE 和整体 MAE。
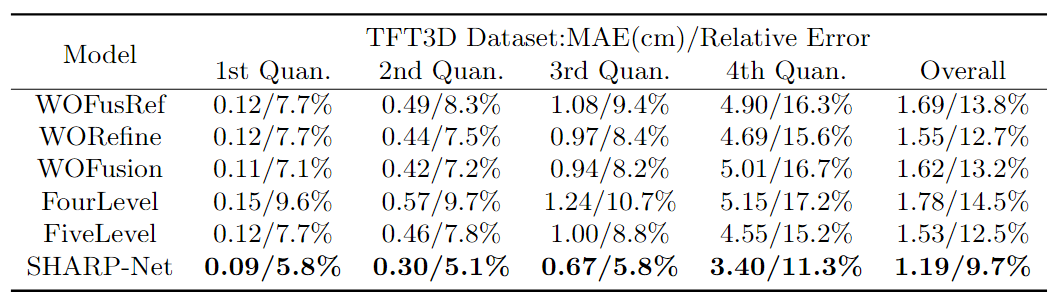表1。与TFT3D数据集上SHARP-Net变体的定量比较。
对于消融研究，我们只使用 TFT3D 数据集将我们的 SHARP-Net 与其变体进行比较。表1报告了每个误差级别的总体MAE和部分MAE。从表1可以看出，SHARP-Net在所有误差级别都达到了最低的MAE和相对误差。此外，与剩余三个分位数相比，"4th Quand."对整体 MAE 值的贡献最大。将 SHARP-Net 与 FourLevel 和 FiveLevel 变体进行比较，我们可以看到，在所有错误级别，MAE 随着金字塔级别总数的增加而增加。这是因为如果金字塔具有更多的层次，网络明确地将场景划分为更详细的层次结构，从而更准确地估计MPI噪声。
将SHARP-Net与WORefine和WOFusion进行比较，可以观察到剩余融合模块和深度细化模块的使用分别降低了26%和23%的整体MAE，这表明这两个模块的必要性。将WORefine和WOFusion在所有误差级别上的比较联系起来，可以看出两个模块中的任何一个都促进了MAE的下降，但程度有限。然而，考虑到WOFusRef和SHARP-Net在MAE和相对误差上的差异，我们得出结论，将这两个模块一起利用可以大大提高噪声去除在所有误差水平下的性能。
5.5合成数据集的结果
为了评估我们提出的SHARP-Net的性能，我们将其与两种最先进的ToF深度去噪方法DeepToF[17]和ToF-KPN[23]进行了比较。所有选定方法的输入是深度图像和相应的振幅图像的串联。需要注意的是，原始 DeepToF 在模型大小方面小于 SHARP-Net。为了公平比较，我们采用与 [23] 相同的策略将原始 DeepToF 模型替换为 ToF-KPN 的 U-Net 主干。TFT3D和FLAT数据集的定量实验结果如表2所示。可以看出，SHARP-Net在两个合成数据集的所有误差水平下都达到了最低的MAE和相对误差。TFT3D 和 FLAT 数据集的输入深度和地面实况深度之间的 MAE 分别为 12.24 cm 和 2.54 cm。在这些数据集上训练后，SHARP-Net 在测试集上将 MAE 分别降低了 1.19 cm 和 0.46 cm。相对误差也是衡量不同方法的性能的一个很好的指标。
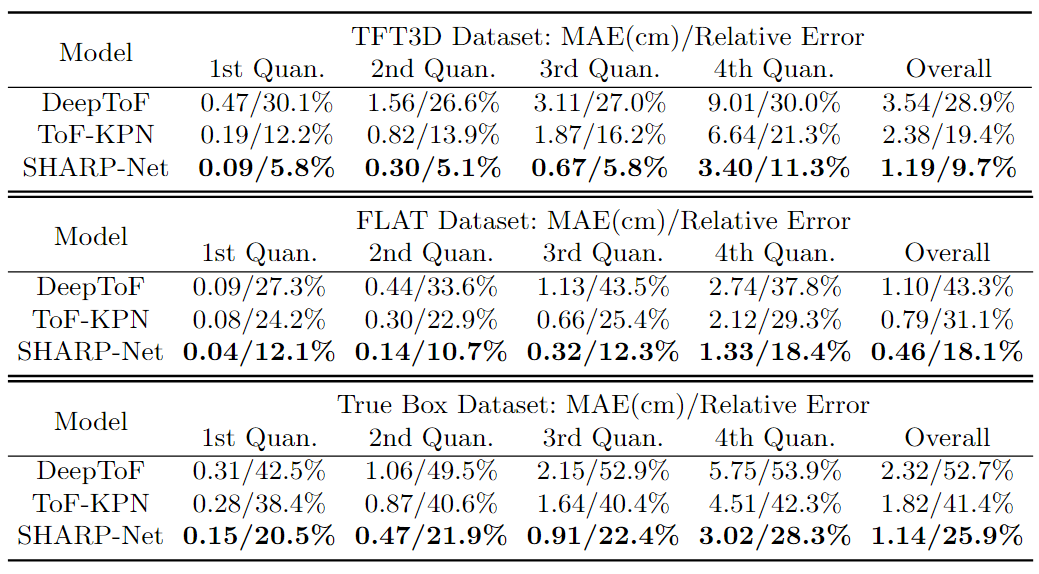表2。TFT3D、FLAT和True Box数据集上具有竞争力的ToF深度去噪方法的定量比较。
从表 2 可以看出，DeepToF 方法对所有四个错误级别都给出了类似的相对误差，尤其是在 TFT3D 数据集上。与其他两种方法相比，DeepToF 在相对误差指标方面的性能较低。对于ToF-KPN，相对误差随着误差水平的提高而增加，这意味着ToF-KPN在较高误差水平集下具有更好的去噪性能。对于SHARP-Net，可以看出相对误差远小于TFT3D数据集上的另外两种方法。在 FLAT 数据集上，SHARP-Net 在相对误差方面优于 DeepToF。与 ToF-KPN 相比，SHARP-Net 在前三个错误级别的性能与 ToF-KPN 相同，并且在最高错误级别优于 ToF-KPN。
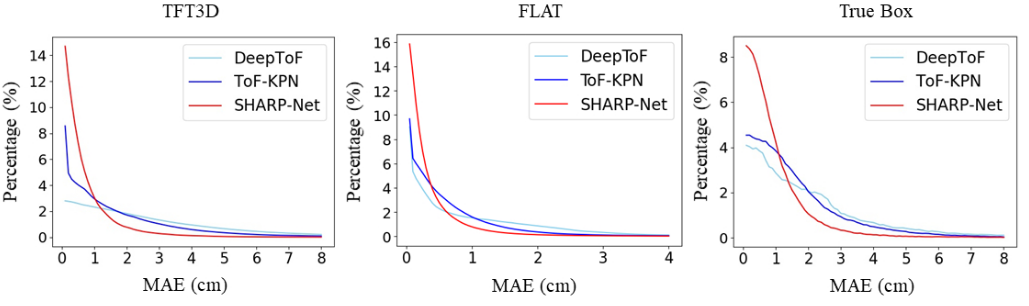图4所示。不同方法在TFT3D、FLAT和True Box数据集上的逐像素误差分布曲线。这三种方法的分布曲线表明，我们提出的SHARP-Net在所有数据集上都获得了最优误差分布。
为了直观比较，在图4中，我们说明了TFT3D和FLAT数据集上所有方法的每像素误差分布曲线。可以看出，在我们的SHARP-Net去噪后，深度误差主要集中在较低的误差区域。在图 5 中，我们给出了 SHARP-Net、ToF-KPN 和 DeepToF 的几个定性比较结果。可以看出，我们提出的方法校正的深度图像更准确，保留了场景中更多的几何结构。我们观察到 ToF-KPN 在去除详细结构中存在的噪声方面优于 DeepToF。然而，在大尺寸形状上去除ToF-KPN是不够的。相比之下，SHARP-Net 同时对大尺寸形状和详细结构展示了更好的结果。事实上，我们的SHARP-Net在深度去噪方面也有一些失败案例，例如低反射区域和极其复杂的几何结构，这是我们方法的局限性。
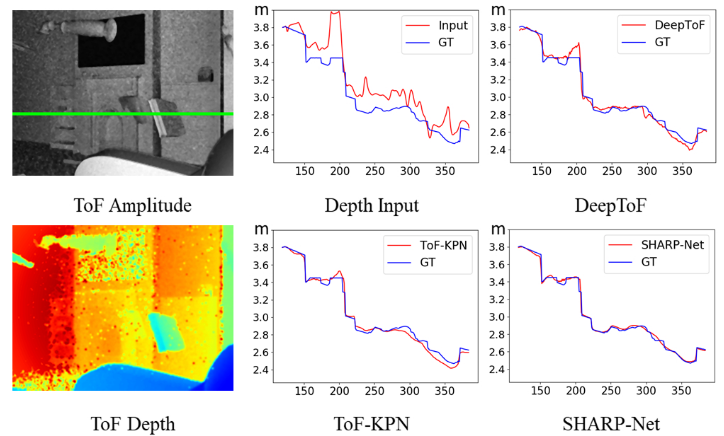图6所示。与TFT3D数据集中深度图像中绿色扫描线的先前工作进行定量比较。'GT' 表示地面实况深度。我们提出的SHARP-Net在深度去噪方面表现出了最好的性能
在图 6 中，我们比较了所有方法在从 TFT3D 数据集中选择的深度图像上的扫描线上的性能。从ToF振幅图像中，我们可以观察到场景位于客厅。许多不同的物体出现在客厅，并展示了复杂的层次结构。沿该扫描线的不同深度变化使其适合这种比较。可以看出，经过深度去噪后，SHARPNet校正的深度数据绘制到地面真值最近的线。
5.6 真实数据集的结果
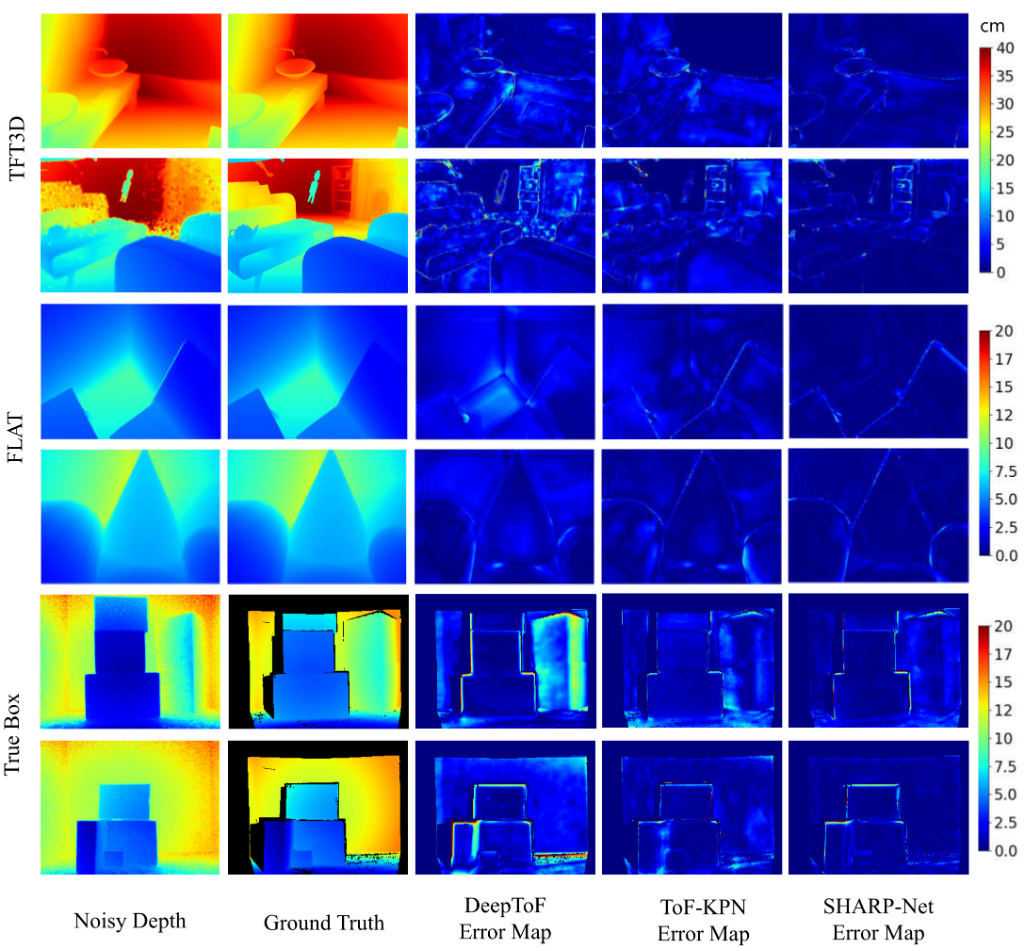图5所示。TFT3D数据集、FLAT数据集和True Box数据集进行ToF深度去噪的定性比较。对于每个数据集，选择两个场景进行比较。右边的颜色条显示了单位在cm处的误差图的颜色刻度。
此外，我们在真实数据集上测试我们提出的 SHARP-Net 以及以前的方法。所有测试的模型都在 True Box 训练集上重新训练。True Box 数据集上所有方法的实验结果也如表 2 所示。可以看出，SHARP-Net 在所有错误级别上都超过了其他方法。我们还发现 True Box 数据集上所有错误级别的相对误差明显大于合成数据集上的相对误差。一个原因可能是真实ToF深度噪声的噪声生成机制更加复杂，这在合成数据集上不能准确地建模。从图4可以看出，True Box数据集上SHARP-Net的误差分布曲线与两个合成数据集的误差分布曲线相似。与其他方法相比，在SHARP-Net去噪后，剩余的深度误差在数据集集中在小值区域。在图 5 的底部，我们展示了从 True Box 测试集中选择的两个场景的定性比较结果。我们可以观察到，对于这个数据集，SHARP-Net 呈现出最好的视觉效果。与其他方法相比，SHARP-Net在大尺寸形状上表现更好，特别是在背景区域
6.结论
多路径干扰(MPI)严重降低了ToF传感器捕获的深度图像。在这项工作中，我们提出了SHARP-Net，一种用于ToF深度去噪的空间层次感知残差金字塔网络。我们的SHARP-Net逐渐利用场景的空间层次结构回归不同尺度的深度残差图，得到残差金字塔。引入了残差融合模块，通过对金字塔中所有级别的深度残差图求和来选择性地融合残差金字塔，并采用基于核预测网络的深度细化模块进一步消除散粒噪声。消融研究验证了这些模块的有效性。实验结果表明，我们的SHARP-Net在合成数据集和真实数据集上的定量和定性比较方面都大大超过了最先进的方法。