🎬 胖咕噜的稞达鸭 :个人主页
🔥 个人专栏 : 《数据结构》《C++初阶高阶》《算法入门》
⛺️技术的杠杆,撬动整个世界!


AVL树的结构:
AVL树相比二叉树多了平衡因子和parent指针(用来更新平衡因子)。
首先AVL树的节点我们需要封装到一个结构体AVLTreeNode中进行说明,这个节点的结构体中有一个键值对,pair<K,V>_kv;是用来存储节点的键值对的,在关联式容器中,每个节点都需要保存"键"和"值"的组合,如果要插入一个元素,需要明确插入的键是什么,对应的值是什么。_kv就是来存储这些信息的。还需要定义一个AVLTreeNode<K,V>类型的指针_left,用于指向当前节点的左子节点。定义一个指针_right,用于指向当前节点的右子节点,_parent用于指向当前节点的父节点。还需要有一个整型成员变量_bf,即平衡因子。
定义一个AVLTreeNode的构造函数,参数是一个 pair<K,V>类型的常量引用kv,用于初始化节点的键值对数据。对_left,_right,_parent这些指针初始化为nullptr,表示当前的节点初始化没有左节点,右节点,父节点,平衡因子是0.表示初始化节点的左右子树高度相同。
在AVLTree树中,树的根节点为nullptr。
cpp
#pragma once
#include<iostream>
#include<map>
#include<set>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{
pair<K, V>_kv;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf;
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
{ }
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
private:
Node* _root = nullptr;
};AVL树的节点插入
如果要插入,先判断插入的节点与当前节点进行对比,小于的插入到左边,大于的插入到右边,如果相等就返回false,这一步也就是去重操作,跟父亲节点进行对比,如果大于父亲节点,那就插入到父亲节点的右边,小于父亲节点就插入到父亲节点的左边。
这些步骤跟二叉搜索树是类似的,接下来看一看不一样的地方在哪里,AVL树需要更新平衡点,就需要父节点的链接,将cur->_parent=parent,链接好了之后,开始了解平衡因子是怎么运作的?
平衡因子的更新:
平衡因子=右子树高度-左子树高度
只有子树高度变化才会影响平衡因子的变动。
插入一个节点会引起平衡因子的变动,如果新增节点在parent的右子树,parent的平衡因子++,新增节点在parent的左子树,parent的平衡因子--。
parent所在子树的高度决定了是否会继续向上更新。
更新停止的条件:
第一种情况:更新平衡因子之后parent=0,说明在更新之前parent是-1或者1,
要么是原来有左子树,parent=-1,之后插入了右子树,parent ++ =0;
要么是原来有右子树,parent=1,之后插入了左子树,parent -- -- =0。
第二种情况:更新平衡因子之后parent=-1或者1,说明在更新之前parent是0
说明在更新之前,左右子树的高度是一样的,新插入的节点打破了这一平衡,
新插入节点在左子树,parent=-1;新插入节点在右子树,parent=1。
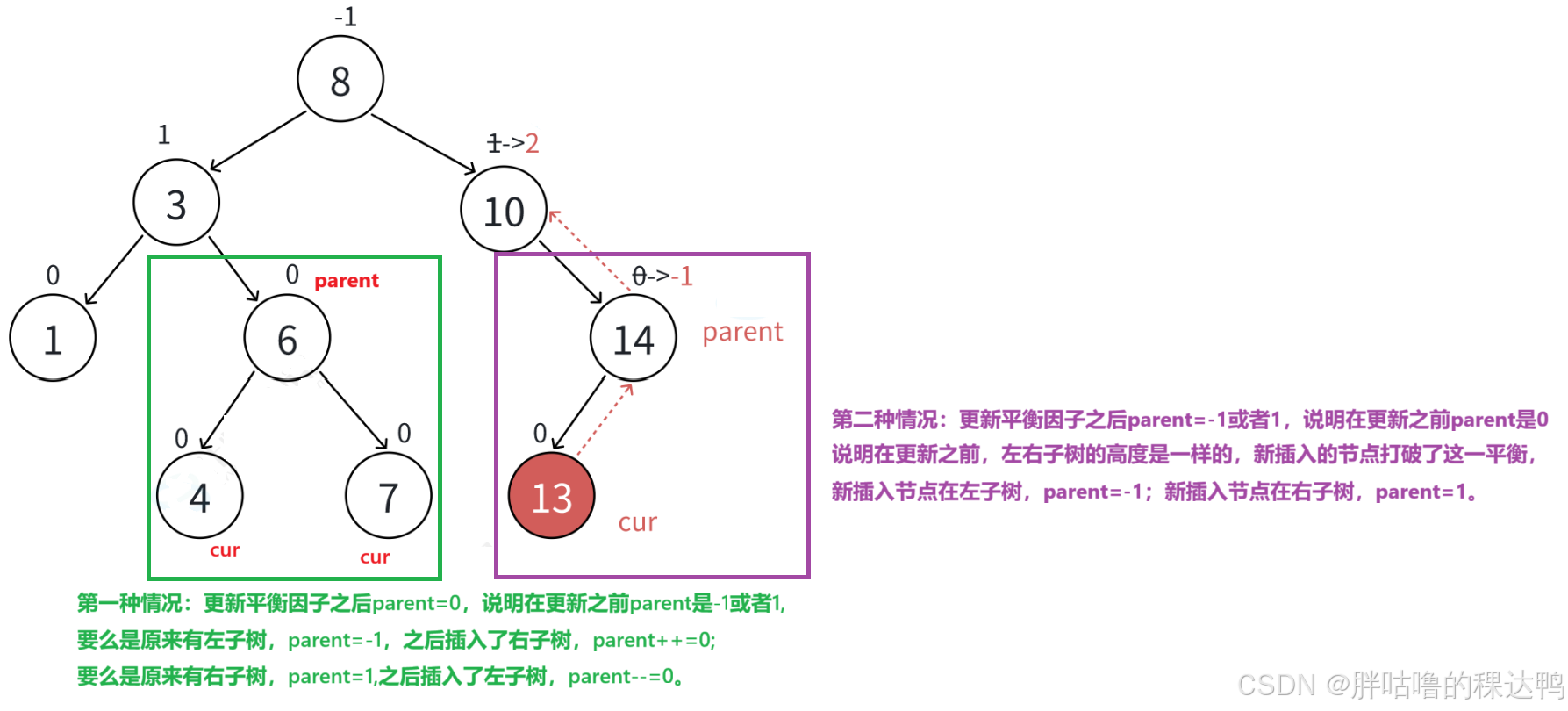
第三种情况:
更新平衡因子之后的parent是2或者-2.
也就是说更新之前的parent是1,新插入了节点,影响了右子树的变化,更新parent为2
更新之前的parent是-1,新插入了节点,影响了左子树的变化,更新parent为-2.
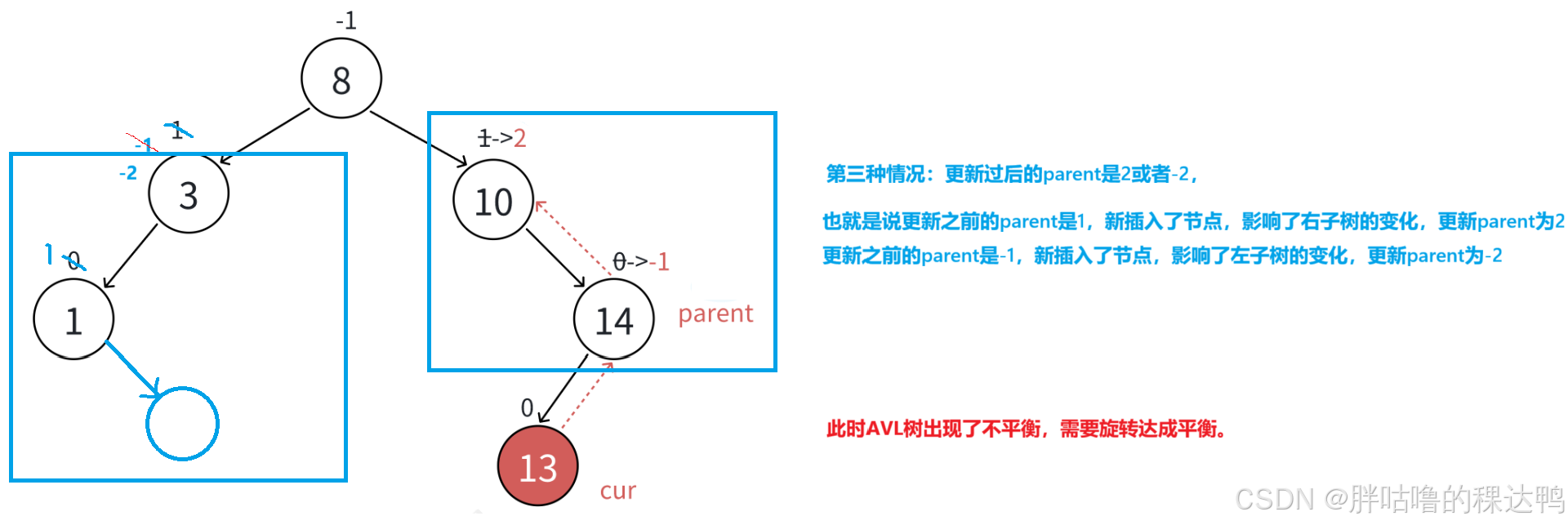
cpp
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
bool insert(const pair<K, V>& kv)
{
if (_root == nullptr) { _root = new Node(kv); return true; }
Node* cur = _root; Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; }
else if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; }
else { return false; }
}
cur = new Node(kv);
if (parent->_kv.first > kv.first) { parent->_left = cur; }
else { parent->_right = cur; }
cur->_parent = parent;//链接父亲
//更新平衡因子
while (parent)
{
if (cur = parent->_right) parent->_bf++;
else parent->_bf--;
if (parent->_bf == 0) { break; }
else if (parent->_bf == -1 || parent->_bf == 1) {cur= parent ; parent = parent->_parent; }
else if (parent->_bf == -2 || parent->_bf == 2)
{
//这里树已经不平衡了,所以要进行旋转处理
break;
}
else{ assert(false); }
}
return true;
}
private:
Node* _root = nullptr;
};旋转的说明:
记住:旋转是因为不平衡所以旋转。哪一端高就需要被优化,右边高向左旋转,调整为一样高的(左单旋);左边高向右旋转,调整为一样高的(右单旋)。
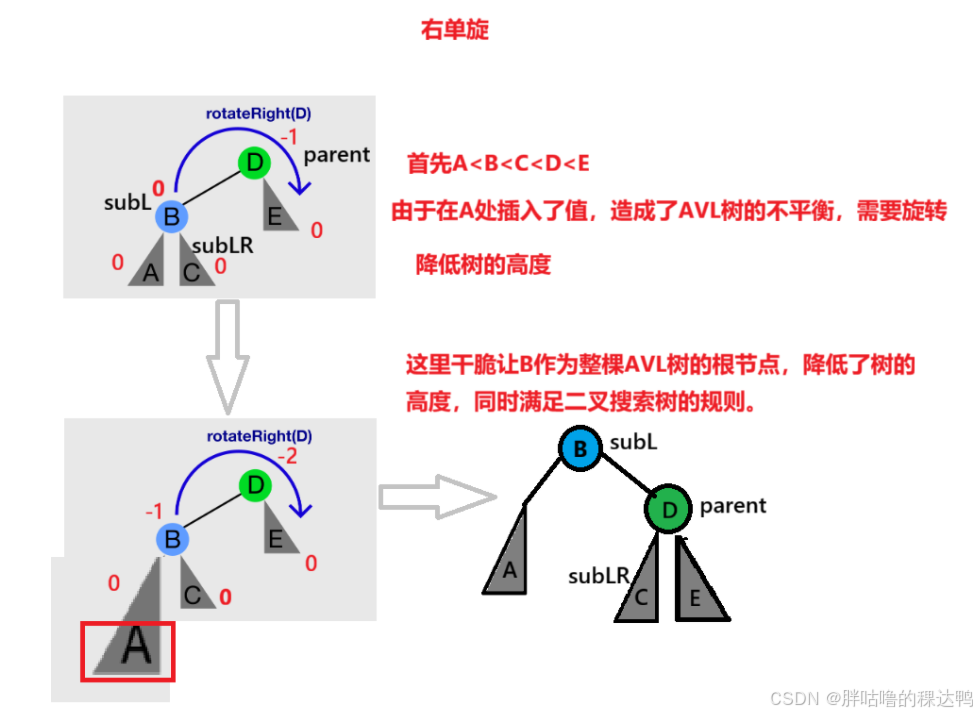
这里看图画的很清楚,首先要给节点命名,Node* subL=parent->_left,subL作为parent的左子树节点,Node* subLR=subL->_right,subLR作为subL的右子树节点,旋转的时候,让parent->_left指向subLR。至少图中是这样子完成右单旋的。实际上,图中和代码实际的操作是不一样的。
这里需要改进:那么subLR的位置为空该怎么办?
如果直接让subL->_right=subLR,此时的subLR是不能直接指向parent节点(看原图中),所以这里也需要改进一下。
接着上述代码,if(subLR!=nullptr),subLR->_parent=parent;不为空就可以指向parent.
修改父亲的指向,subL->_right=parent;parent->_parent=subL;
还需要该进:如果更新好了之后,这些节点是一个大AVL树的一部分呢,还需要向上进行调整
这里我们这样来设定,如果父亲节点为根节点_root,那么就让父亲节点的父亲节点为根节点,这里又发现我们之前设置的一个漏洞,在旋转更新新的父亲节点的时候,要把旧的父亲节点的父亲保存起来,也就是说要提前保存好爷爷节点。Node* grandParent = parent->_parent;
如果父亲节点为根节点,也就是说爷爷节点指向空,此时这个_root=subL,而且还要进行链接,subL->_parent = nullptr;
如果爷爷节点不为空,也就是说我们旋转的这一部分是大AVL树的一部分,如果旋转的这一部分在爷爷节点的左子树,链接grandParent->_left=subL;如果链接的这一部分在爷爷的右子树,链接grandparent->_right=subL,然后还要申明一下subL->_parent=grandparent
最后改一下平衡因子:parent->_bf = subLR->_bf = 0。
上代码!
cpp
//右单旋
void rotateRight(Node* parent)
{
//定义节点
Node* subL = parent->_left;
Node* subLR = subL->_right;
//开始旋转:先认子再认父
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* grandParent = parent->_parent;//保存爷爷节点
subL->_right = parent;
parent->_parent = subL;
//判断是不是AVL子树或者整个AVL树
//是整个AVL树
if (parent==_root) { _root = subL; subL->_parent = nullptr; }
else
{
//子树,原根是爷爷节点左节点,现在是爷爷节点左节点指向新根
if (parent == grandParent->_left) { grandParent->_left = subL; }
else { grandParent->_right = subL; }
subL->_parent = grandParent;
}
//更新平衡因子
parent->_bf = subL->_bf = 0;
}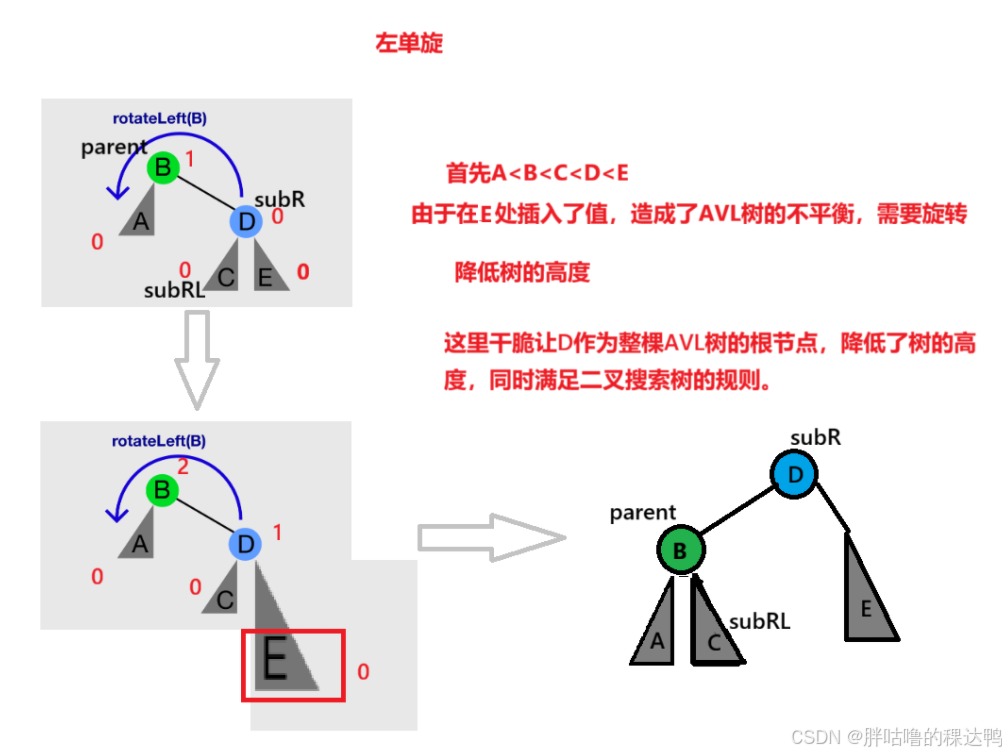
左单旋:
先定义subR和subRL的指针指向,然后开始左旋,先让parent的左子树指向subRL,再来判断,subRL是不是指向为空,不为空,就可以让subRL的父亲节点跟parent进行链接。
然后subR的左子树指向parent,parent的父亲节点指向subR,这样就做好了链接,
再来判断左单旋的这一部分是不是大AVL树的一部分,这样就要先在左单旋节点链接之前保存好爷爷节点的指针,Node* grandParent=parent->_parent;
如果爷爷节点为空,那么就说明我们刚单旋的一部分,subR是根节点,而且这个subR的父亲节点要置为空;
如果爷爷节点不为空,那么:原来爷爷节点指向左子树是parent,现在替换为爷爷节点指向左子树是subR;
原来爷爷节点指向右子树是parent,现在替换为爷爷节点指向右子树是subR.
然后需要申明subR的父亲节点是爷爷节点。
最后更新一下平衡因子。
cpp
//左单旋
void rotateLeft(Node* parent)
{
//定义节点
Node* subR = parent->_right;
Node* subRL = subR->_left;
//旋转:先认子再认父
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* grandParent = parent->_parent;//保存爷爷节点
subR->_left = parent;
parent->_parent = subR;
//判断是不是AVL子树或者整个AVL树
//是整个AVL树
if (parent==_root) { _root = subR; subR->_parent = nullptr; }
else
{//子树,原根是爷爷节点左节点,现在是爷爷节点左节点指向新根
if (parent == grandParent->_left) { grandParent->_left = subR; }
else { grandParent->_right = subR; }
subR->_parent = grandParent;
}
//更新平衡因子
parent->_bf = subR->_bf = 0;
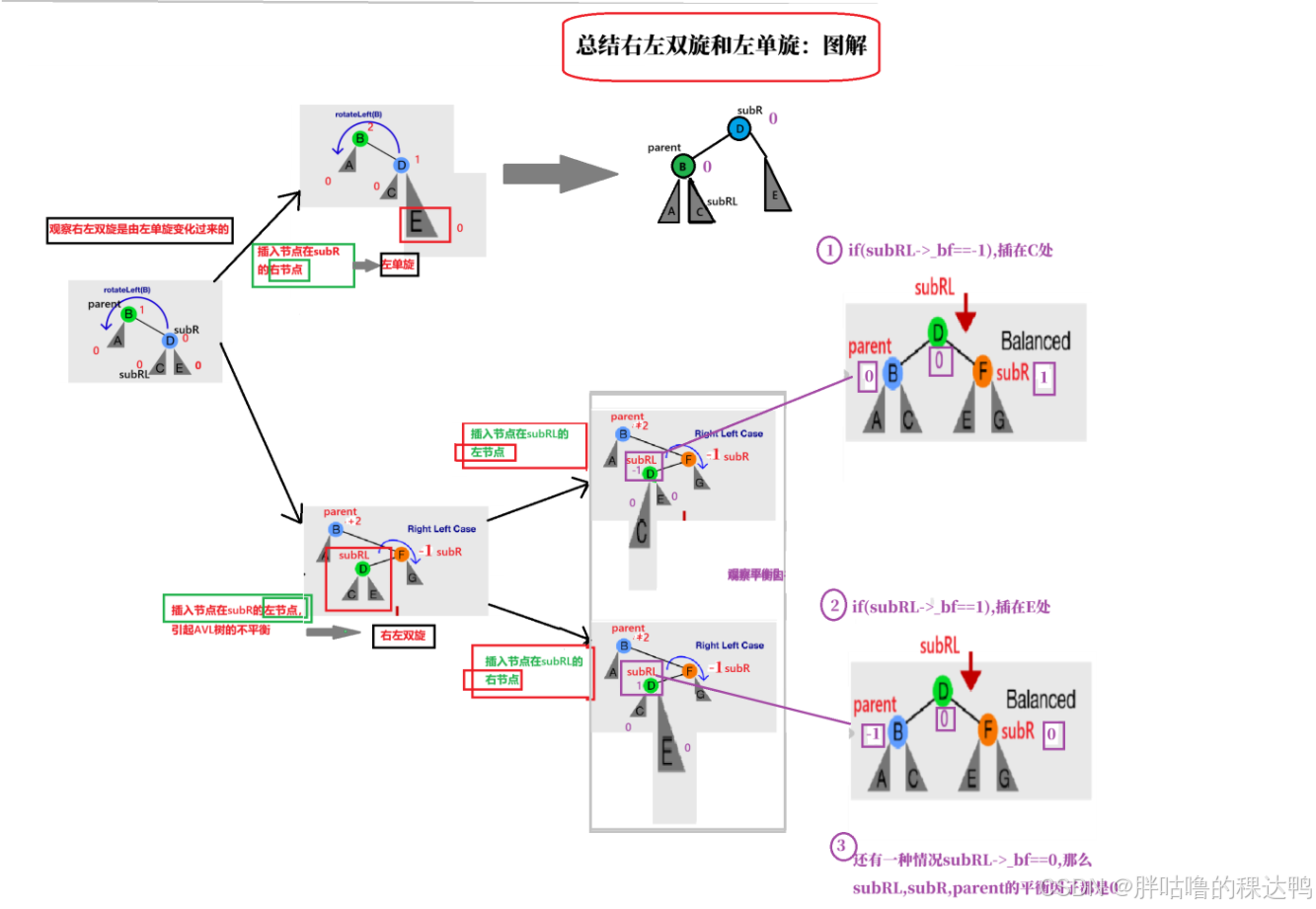
}左右双旋:
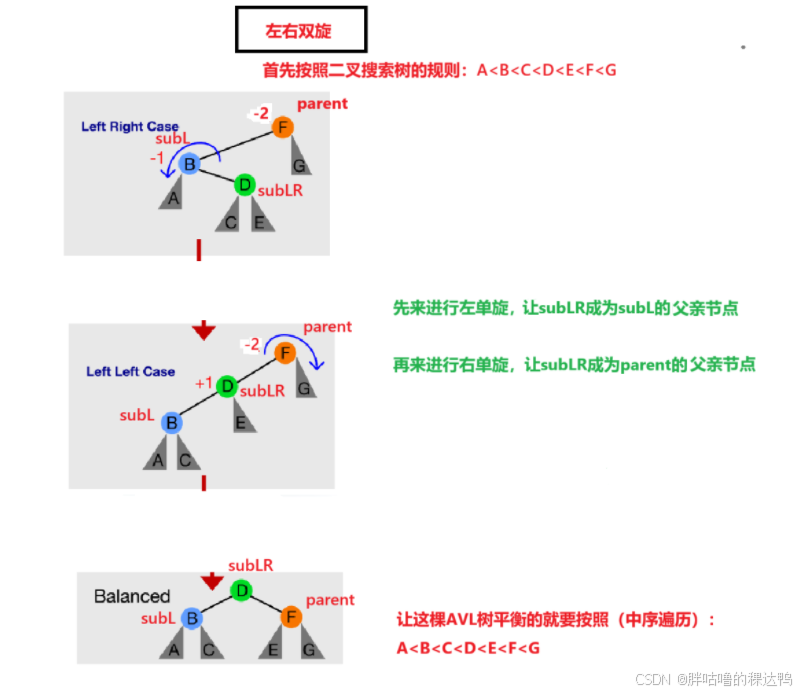
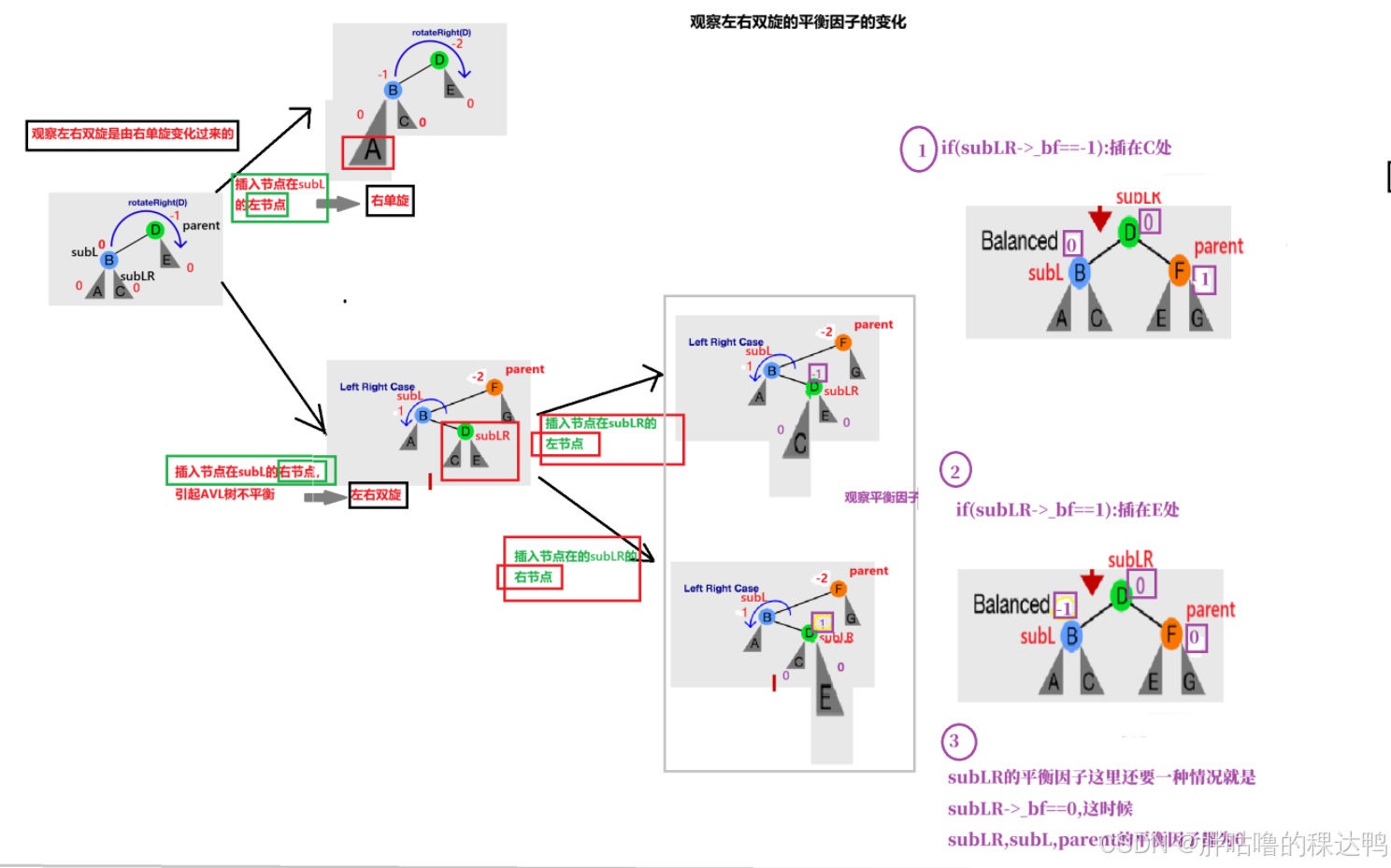
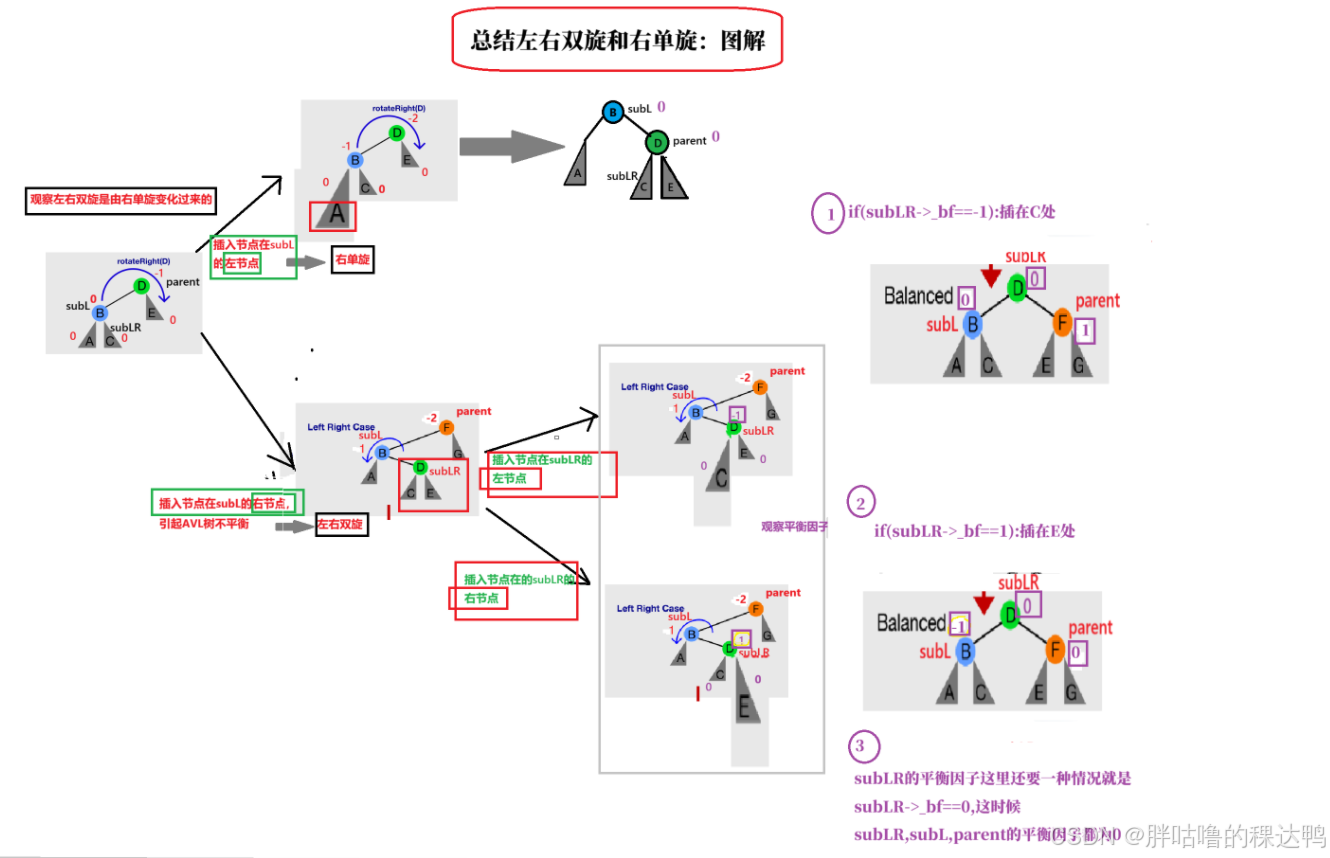
演化规则:
先进行左单旋:插入节点subLR部分太高了,右边太高往左边旋转变平衡,降低树的高度,这一部分将以父亲节点的根为旋转点,parent->_left,可以直接调用左单旋的代码,rotateLeft(parent->_left),
然后进行右单旋:调正之后使得左边变高了,所以再次往右边进行调整,这里可以直接调用右单旋的代码,旋转点是parent. rotateRight(parent)
这一步就大致完成了我们的左右双旋步骤。
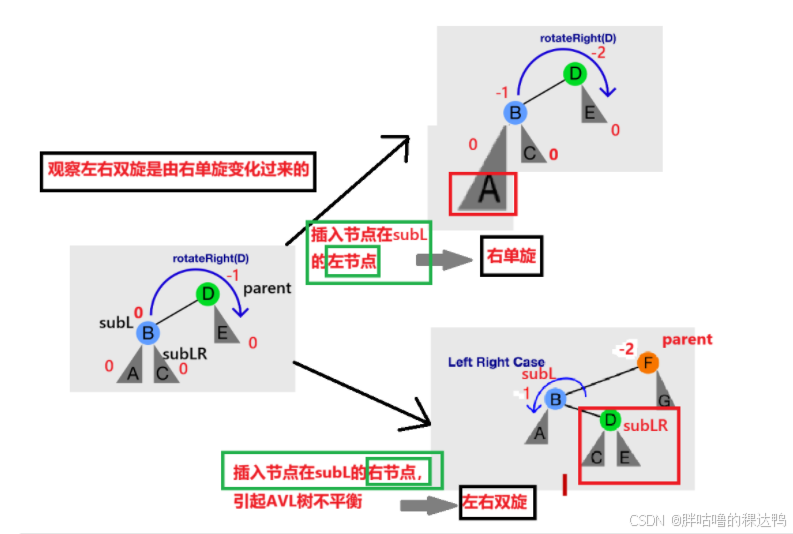
但是: (这些要放在调用左单旋,右单旋的前面进行记录)(为什么博主没有放在前面,目的是梳理代码完成的过程。)
上述调用左单旋,右单旋的会将所有的平衡因子改0,但是旋转的时候我们还需要旋转前的节点,所以首先将平衡因子会改变的几个节点(subL,subLR)命名并存储,Node* subL=parent->_left; Node* subLR=subL->_right;
存储新的父亲节点subLR的平衡因子。
然后到了更新平衡因子的一步了:
如果subLR的平衡因子为0,那就说明这个树只有一个根节点,根节点的左节点,还有一个就是subLR的节点(插入在根节点左节点的右边);
如果subLR的平衡因子为-1,那就说明插入的节点插入在C的位置,
cpp
//左右双旋
void RotateLR(Node* parent)
{
//定义节点
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf=subLR->_bf;//记录平衡因子
rotateLeft(parent->_left);//左旋
rotateRight(parent);//右旋
//看图记录平衡因子
if (bf == -1) { subLR->_bf = 0; subL->_bf = 0; parent->_bf = 1; }
else if (bf == 1) { subLR->_bf = 0; subL->_bf = -1; parent->_bf = 0; }
else if (bf == 0) { subLR->_bf = 0; subL->_bf = 0; parent->_bf = 0; }
else { assert(false); }
}总结左右双旋和右单旋:
右左双旋:
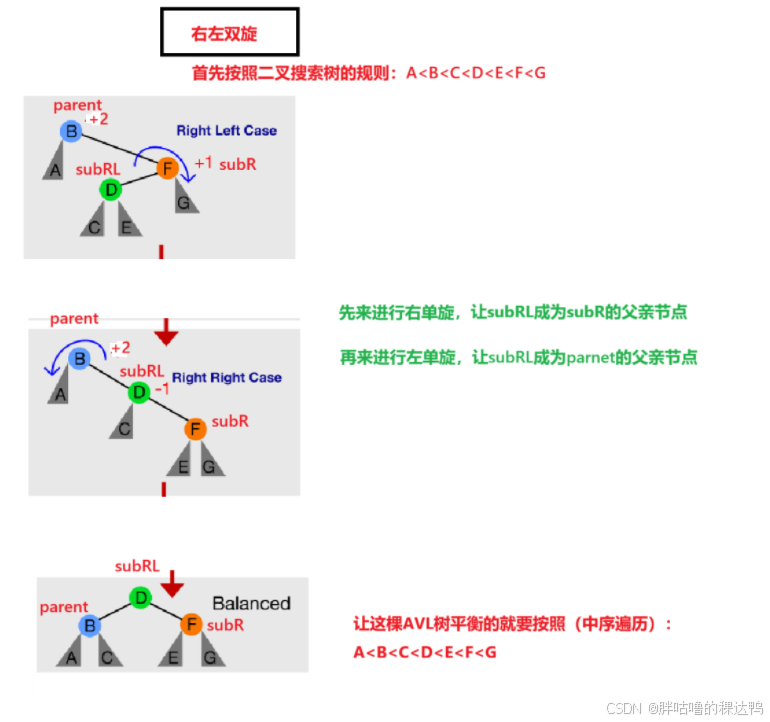
演化规则:
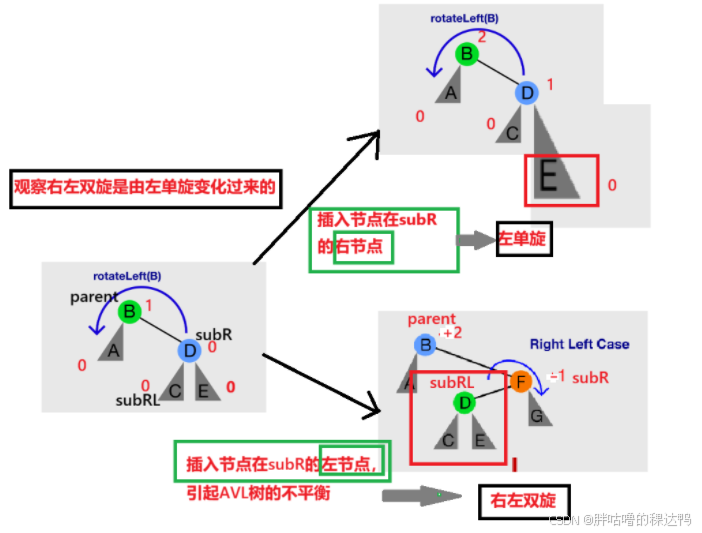
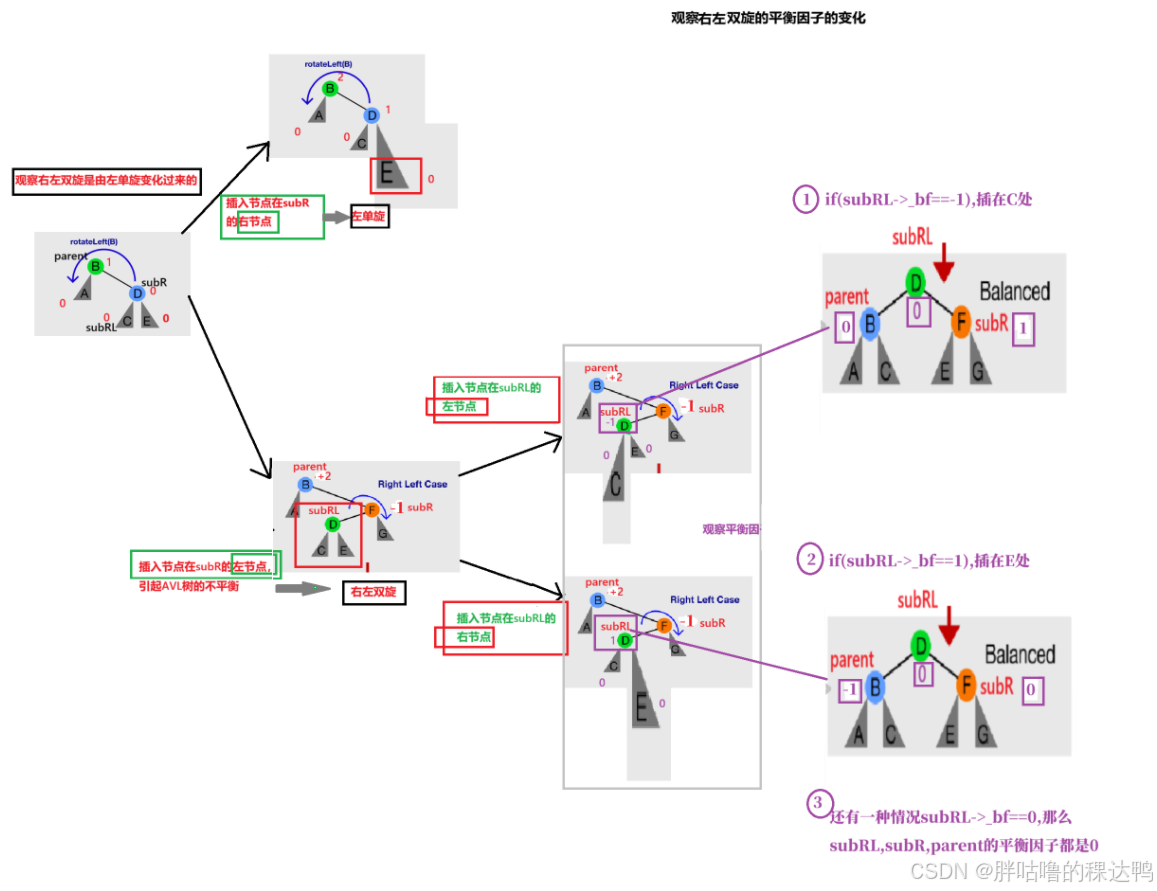
cpp
//右左双旋
void RotateRL(Node* parent)
{
//定义节点
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;//记录平衡因子
rotateRight(parent->_right);//右旋
rotateLeft(parent);//左旋
//看图记录平衡因子
if (bf == -1) { subRL->_bf = 0; subR->_bf = 1; parent->_bf = 0; }
else if (bf == 1) { subRL->_bf = 0; subR->_bf = 0; parent->_bf = -1; }
else if (bf == 0) { subRL->_bf = 0; subR->_bf = 0; parent->_bf = 0; }
else { assert(false); }
}完整的插入代码:
直接来看代码:(看注释)
cpp
bool insert(const pair<K, V>& kv)
{
//如果根节点为空
if (_root == nullptr) { _root = new Node(kv); return true; }
//cur从根节点开始遍历,大于根节点插入到右边,小于根节点插入到左边
Node* cur = _root; Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; }
else if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; }
else { return false; }
}
cur = new Node(kv);
//判断插入到父亲节点的左还是右
if (parent->_kv.first > kv.first) { parent->_left = cur; }
else { parent->_right = cur; }
//链接父亲
cur->_parent = parent;//链接父亲
//更新平衡因子
while (parent)
{
//平衡因子的规则:节点插入到右边,父亲节点++;节点插入到左边,父亲节点--
if (cur == parent->_right) parent->_bf++;
else
parent->_bf--;
if (parent->_bf == 0) { break; }
else if (parent->_bf == -1 || parent->_bf == 1) { cur = parent; parent = parent->_parent; }
else if (parent->_bf == -2 || parent->_bf == 2)
{
//这里树已经不平衡了,所以要进行旋转处理
if (parent->_bf == -2 && cur->_bf == -1) { rotateRight(parent); }
else if (parent->_bf == 2 && cur->_bf == 1) { rotateLeft(parent); }
else if (parent->_bf == -2 && cur->_bf == 1) { RotateLR(parent); }
else if (parent->_bf == 2 && cur->_bf == -1) { RotateRL(parent); }
else { assert(false); }
break;
}
else { assert(false); }
}
return true;
}完整代码:
cpp
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{
pair<K, V>_kv;
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
int _bf;
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_bf(0)
{ }
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
//右单旋
void rotateRight(Node* parent)
{
//定义节点
Node* subL = parent->_left;
Node* subLR = subL->_right;
//开始旋转:先认子再认父
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* grandParent = parent->_parent;//保存爷爷节点
subL->_right = parent;
parent->_parent = subL;
//判断是不是AVL子树或者整个AVL树
//是整个AVL树
if (parent==_root) { _root = subL; subL->_parent = nullptr; }
else
{
//子树,原根是爷爷节点左节点,现在是爷爷节点左节点指向新根
if (parent == grandParent->_left) { grandParent->_left = subL; }
else { grandParent->_right = subL; }
subL->_parent = grandParent;
}
//更新平衡因子
parent->_bf = subL->_bf = 0;
}
//左单旋
void rotateLeft(Node* parent)
{
//定义节点
Node* subR = parent->_right;
Node* subRL = subR->_left;
//旋转:先认子再认父
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* grandParent = parent->_parent;//保存爷爷节点
subR->_left = parent;
parent->_parent = subR;
//判断是不是AVL子树或者整个AVL树
//是整个AVL树
if (parent==_root) { _root = subR; subR->_parent = nullptr; }
else
{//子树,原根是爷爷节点左节点,现在是爷爷节点左节点指向新根
if (parent == grandParent->_left) { grandParent->_left = subR; }
else { grandParent->_right = subR; }
subR->_parent = grandParent;
}
//更新平衡因子
parent->_bf = subR->_bf = 0;
}
//左右双旋
void RotateLR(Node* parent)
{
//定义节点
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf=subLR->_bf;//记录平衡因子
rotateLeft(parent->_left);//左旋
rotateRight(parent);//右旋
//看图记录平衡因子
if (bf == -1) { subLR->_bf = 0; subL->_bf = 0; parent->_bf = 1; }
else if (bf == 1) { subLR->_bf = 0; subL->_bf = -1; parent->_bf = 0; }
else if (bf == 0) { subLR->_bf = 0; subL->_bf = 0; parent->_bf = 0; }
else { assert(false); }
}
//右左双旋
void RotateRL(Node* parent)
{
//定义节点
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;//记录平衡因子
rotateRight(parent->_right);//右旋
rotateLeft(parent);//左旋
//看图记录平衡因子
if (bf == -1) { subRL->_bf = 0; subR->_bf = 1; parent->_bf = 0; }
else if (bf == 1) { subRL->_bf = 0; subR->_bf = 0; parent->_bf = -1; }
else if (bf == 0) { subRL->_bf = 0; subR->_bf = 0; parent->_bf = 0; }
else { assert(false); }
}
bool insert(const pair<K, V>& kv)
{
//如果根节点为空
if (_root == nullptr) { _root = new Node(kv); return true; }
//cur从根节点开始遍历,大于根节点插入到右边,小于根节点插入到左边
Node* cur = _root; Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first > kv.first) { parent = cur; cur = cur->_left; }
else if (cur->_kv.first < kv.first) { parent = cur; cur = cur->_right; }
else { return false; }
}
cur = new Node(kv);
//判断插入到父亲节点的左还是右
if (parent->_kv.first > kv.first) { parent->_left = cur; }
else { parent->_right = cur; }
//链接父亲
cur->_parent = parent;//链接父亲
//更新平衡因子
while (parent)
{
//平衡因子的规则:节点插入到右边,父亲节点++;节点插入到左边,父亲节点--
if (cur == parent->_right) parent->_bf++;
else
parent->_bf--;
if (parent->_bf == 0) { break; }
else if (parent->_bf == -1 || parent->_bf == 1) { cur = parent; parent = parent->_parent; }
else if (parent->_bf == -2 || parent->_bf == 2)
{
//这里树已经不平衡了,所以要进行旋转处理
if (parent->_bf == -2 && cur->_bf == -1) { rotateRight(parent); }
else if (parent->_bf == 2 && cur->_bf == 1) { rotateLeft(parent); }
else if (parent->_bf == -2 && cur->_bf == 1) { RotateLR(parent); }
else if (parent->_bf == 2 && cur->_bf == -1) { RotateRL(parent); }
else { assert(false); }
break;
}
else { assert(false); }
}
return true;
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
private:
void _Inorder(Node* root)
{
if (root == nullptr) { return ; }
_Inorder(root->_left);
cout << root->_kv.first <<":"<< root->_kv.second << endl;
_Inorder(root->_right);
}
private:
Node* _root = nullptr;
};测试:
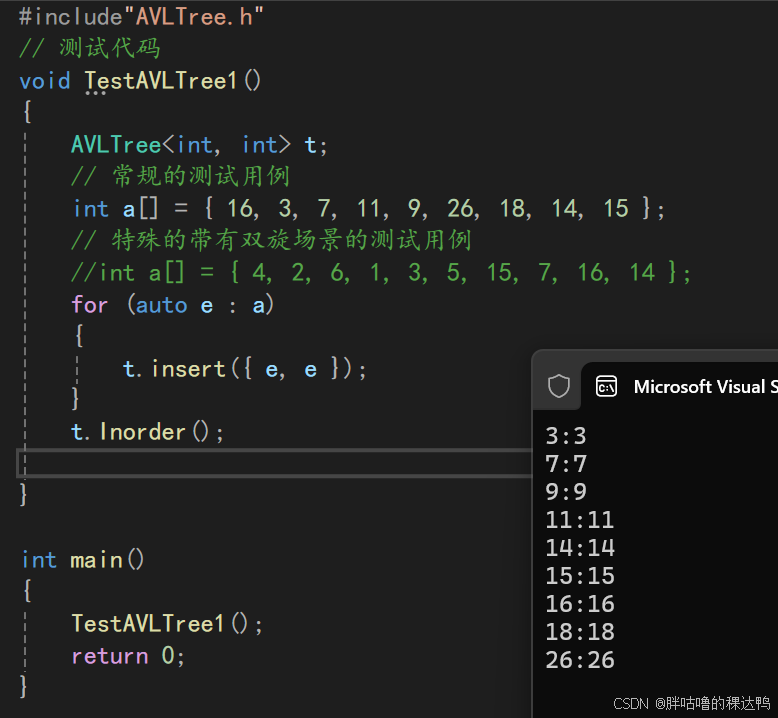
cpp
#include"AVLTree.h"
// 测试代码
void TestAVLTree1()
{
AVLTree<int, int> t;
// 常规的测试用例
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
// 特殊的带有双旋场景的测试用例
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
for (auto e : a)
{
t.insert({ e, e });
}
t.Inorder();
}
int main()
{
TestAVLTree1();
return 0;
}