算法练习：双指针专题

1、移动零

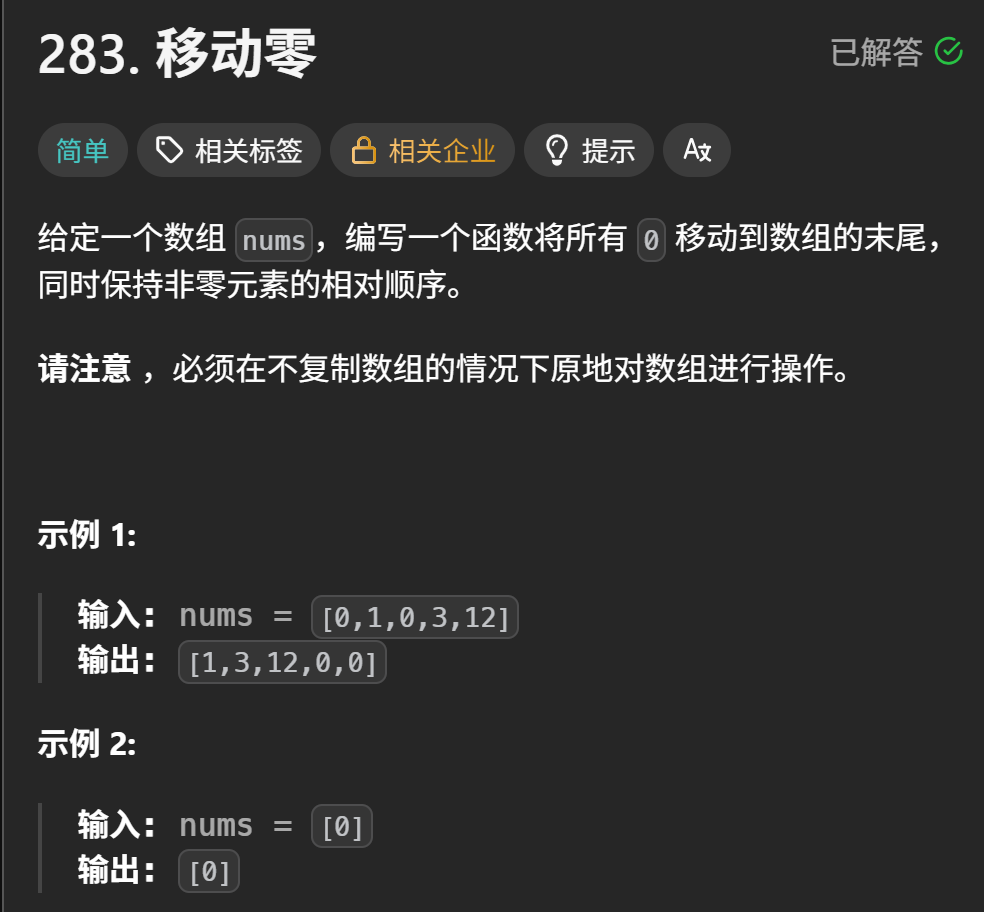
定义两个指针dest和cur

cur:遍历整个数组，寻找非零元素（初始为 0）。

dest:指向已处理区间的最后一个非零元素（初始为 -1，表示还没有非零元素）

核心思路 ：

当 cur 遇到非零元素时，将其交换到 dest+1 的位置（即已处理非零区间的下一个位置），然后 dest 右移一位，cur右移一位。这样就划分为了3个区间：

$0, dest\] 区间内的元素都是非零且顺序不变的；$
$cur, n-1\] 区间内的元素是未处理的。$

cpp 复制代码

void moveZeroes(vector<int>& nums) 
{
        int cur = 0;
        int dest = -1;
        while(cur < nums.size())
        {
            if(nums[cur] != 0)
            {
                swap(nums[++dest],nums[cur]);
            }
            cur++;
        }
}

时间复杂度：O(n)，仅遍历数组一次，每个元素最多被交换一次。

空间复杂度：O(1)，仅使用两个指针，没有额外空间。

为什么这方法有效？

保持顺序：非零元素被依次放到 dest 位置，相当于"追加"到非零区间的末尾，不会打乱原有顺序。

原地修改：不需要额外数组，直接修改原数组，空间效率高。

2、复写零

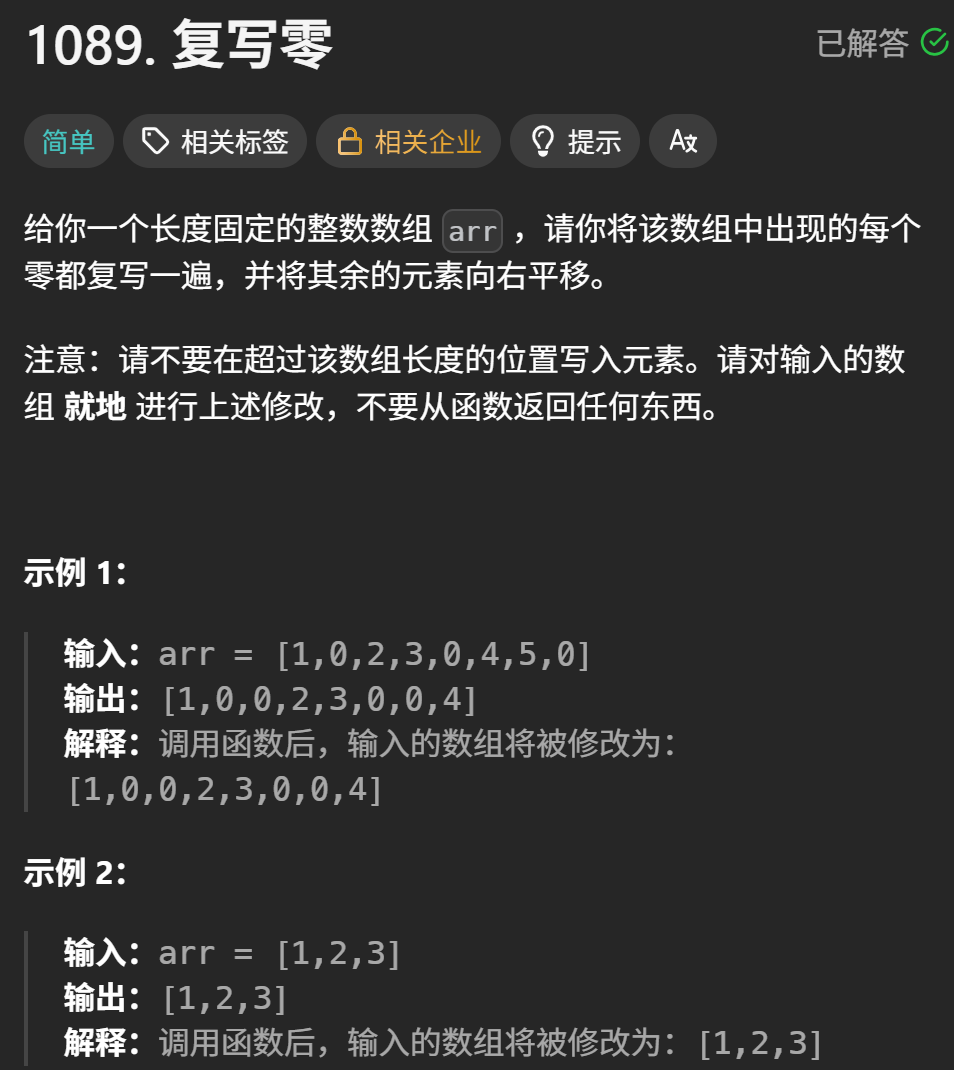
为什么不用"直接遍历+插入"？比如遇到0就插入一个0，后面元素后移？

缺点：直接插入会覆盖未处理的元素（比如原数组中的0后面的元素会被提前移动，导致后面的0无法正确复制），且时间复杂度为O(n²)（每次插入都要移动后面所有元素），效率太低。

核心思路：

"先找终点，再从后往前填"
定义两个指针：
- cur：从左到右遍历原数组的指针，标记当前要处理的元素位置（初始为 0）；
- dest：假设数组"扩容"后的指针（遇0加2，遇非0加1），标记当前元素"应该在"的位置。（初始为 -1）

第一步：找到最后一个需要复制的元素

遍历cur，直到cur < 数组长度：

若arr[cur]是0，dest加2（要复制一个0）；
若arr[cur]非0，dest加1（不需要复制）；

检查dest是否超过数组长度（dest >= n-1）：

若是，停止遍历，此时cur的位置就是最后一个需要处理的元素（再往后处理会超出数组长度）；否则，cur加1，继续遍历。

第二步：处理边界情况

边界场景：当dest刚好等于数组长度（dest == n）时，说明最后一个元素是0，且这个0只能复制一次（数组长度不够）

把数组最后一个位置（n-1）设为0（复制一次）；
cur减1（回退到上一个元素）；
dest减2（回退到上一个"应该在"的位置）。

第三步：从后往前填元素

为什么从后往前？

从前往后填会覆盖未处理的元素（比如cur=1的0还没处理，就被cur=0的元素覆盖）；而从后往前填，dest的位置是"扩容"后的终点，不会覆盖未处理的元素。

cpp 复制代码

void duplicateZeros(vector<int>& arr) 
    {
        int n = arr.size();
        int cur = 0, dest = -1;
    
    // 1.找到最后一个数
        while (cur < n) 
        {
            if (arr[cur] == 0) 
            {
                dest += 2;
            } 
            else 
            {
                dest += 1;
            }

            if (dest >= n - 1) 
            { 
                break;
            }
            cur++;
        }
    
    //2.处理边界情况
        if(dest == n)
        {
            arr[n - 1] = 0;
            cur--;
            dest -= 2;
        }

        //3.从后往前复写
        while(cur >= 0)
        {
            if (arr[cur] == 0) 
            {
                arr[dest--] = 0;
                arr[dest--] = 0;
            } 
            else 
            {
                arr[dest--] = arr[cur];
            }
            cur--;

        }
        
    }

3、快乐数

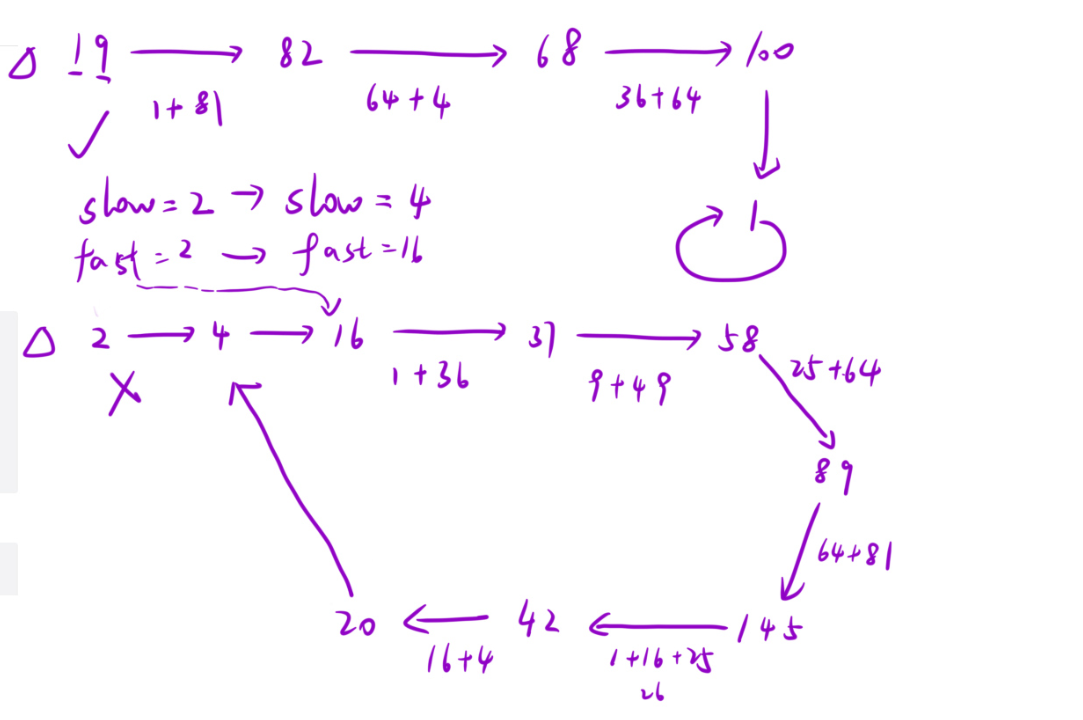
核心思想：

定义快慢指针，快指针走两步，慢指针走一步，快指针追上慢指针说明该数是快乐数

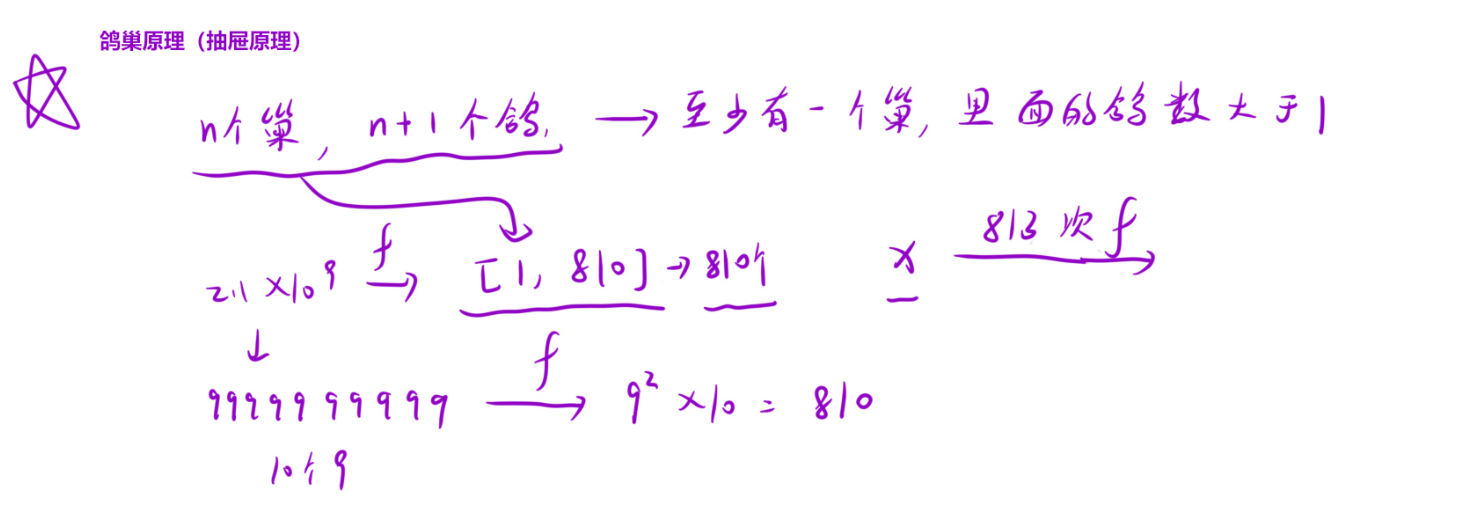
根据鸽巢原理，它一定不会无限张开下去，一定成环

cpp 复制代码

int bitsum(int n)
    {
        int sum = 0;
        while(n)
        {
            int t = n % 10;
            sum += t * t;
            n /= 10;
        }
        return sum;
    }

    bool isHappy(int n) {
        int slow = n;
        int fast = bitsum(n);
        
        while(slow != fast)
        {
            slow = bitsum(slow);
            fast = bitsum(bitsum(fast));
        }
        return slow == 1;
    }

4、盛最多水的容器

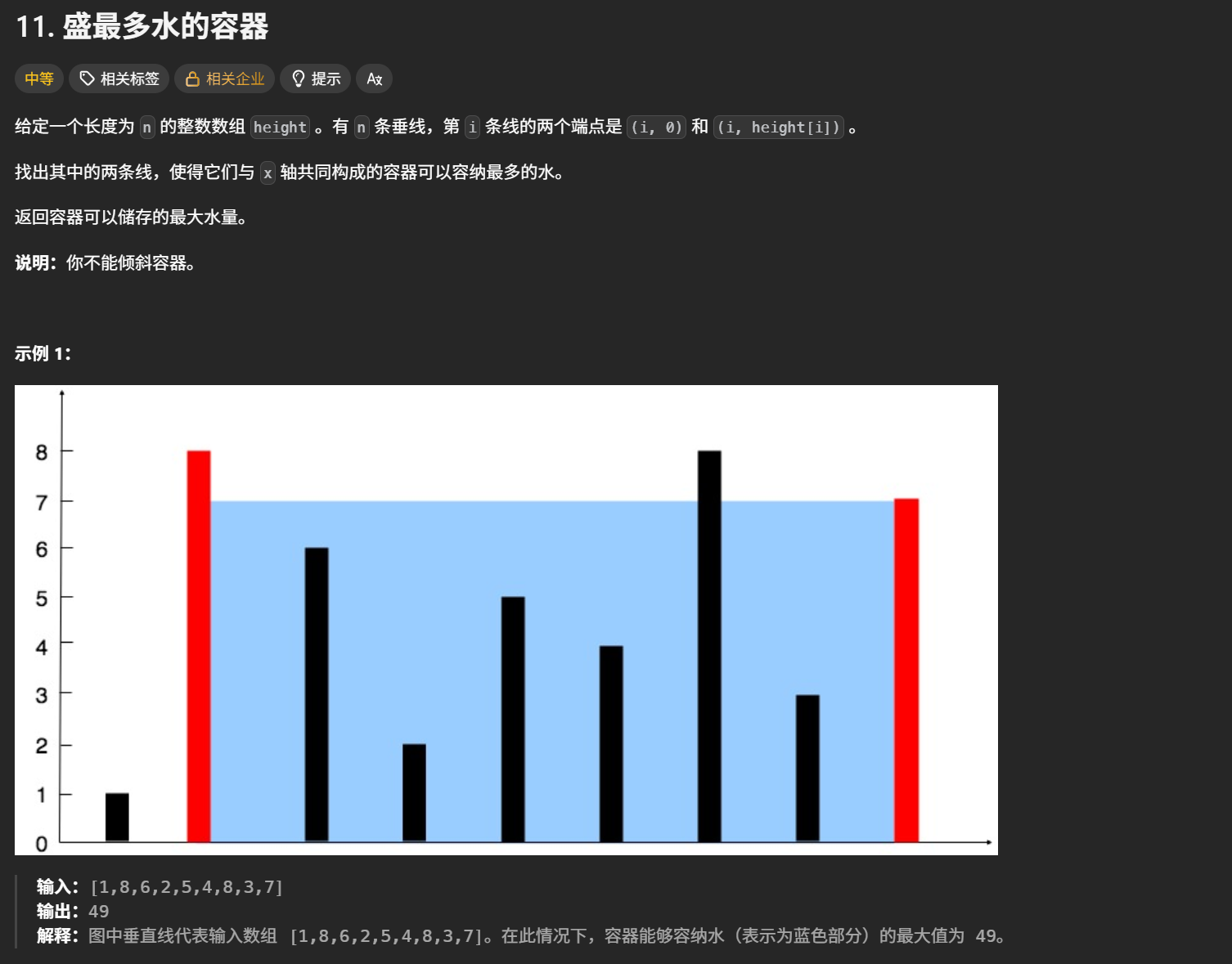
暴力解法就是用两个for循环一个个枚举求出最大值

核心思想：

定义两个指针，一个指向头left，一个指向最后一个元素right，因为此时款最大，让他们向内移动
他们向内移动，由 V = w * h,我们可以分析出两种情况，（1）要么宽和高同时减小，要么宽减小（因为高以小的那一边为主，如果一直是1，那么不就是高不变，只有宽在减小嘛），不管是哪一种情况V总体就是减小的
因此，我们比较左右指针对应的高度，小的那一边就往左或右移动（比如left = 0 -> h =1,right = 8 -> h = 7, v = 1 * 8 = 8,接着right往左移动，w逐渐减小，高度依旧是1，V逐渐减小，我们要找最大的，那么中间这个范围的体积还有必要算吗？总是没有第一次大），因此在此之前，我们先算出当前的体积，在进行判断移动
最后比较这些V，找出最大的V

cpp 复制代码

int maxArea(vector<int>& height) {

        int left = 0;
        int right = height.size() - 1;
        int ret = 0;
        while(left <= right)
        {
            int v = min(height[left],height[right])*(right - left);
            ret = max(ret,v);
            if(height[left] > height[right])
                right--;
            else
                left++;
        }
        
        return ret;
    }

5、有效三角形个数

1. 问题定义

给定一个包含非负整数的数组 nums，你需要统计数组中可以组成三角形三条边的三元组 (nums[i], nums[j], nums[k]) 的个数。

2. 核心思想（三角形不等式）

构成三角形的三条边 a , b , c a, b, c a,b,c 必须满足三角形不等式：

a + b > c a + b > c a+b>c
a + c > b a + c > b a+c>b
b + c > a b + c > a b+c>a

如果我们先对数组进行排序，假设 a ≤ b ≤ c a \le b \le c a≤b≤c，那么我们只需要满足一个条件： a + b > c a + b > c a+b>c。

（因为 a + c > b a+c > b a+c>b 和 b + c > a b+c > a b+c>a 在 c c c 是最大边时自动成立）。

3. 算法分解

你的代码正是利用了这一特性。

步骤一：排序

cpp 复制代码

sort(nums.begin(),nums.end());
int n = nums.size();

首先对数组进行升序排序。这是使用双指针法的前提。

时间复杂度 : O ( n log ⁡ n ) O(n \log n) O(nlogn)

步骤二：外层循环（固定最长边 c）

cpp 复制代码

int ret = 0;
for(int i = n - 1; i > 0; i--)
{ 
    int maxc = nums[i]; // maxc 就是我们固定的最大边 c
    ...
}

代码采用从后往前 遍历的方式，固定 nums[i] 作为三角形的最长边 c c c ( maxc )。

我们接下来需要在 nums[0...i-1] 这个子数组中，寻找两个数 a a a 和 b b b，使得 a + b > maxc a + b > \text{maxc} a+b>maxc。

步骤三：内层循环（双指针查找 a 和 b）

cpp 复制代码

    int left = 0;
    int right = i - 1;
    while(left < right)
    {
        ...
    }

我们在子数组 nums[0...i-1] 上使用双指针：

left 指针指向 a a a (从最小的可能值 n u m s [ 0 ] nums[0] nums[0] 开始)。
right 指针指向 b b b (从最大的可能值 n u m s [ i − 1 ] nums[i-1] nums[i−1] 开始)。

步骤四：核心判断与计数

cpp 复制代码

        if(nums[left] + nums[right] > maxc)
        {
            ret += right - left;
            right--;
        }
        else
        {
            left++;
        }

这是整个算法最精妙的部分：

if (nums[left] + nums[right] > maxc)
- 这满足了 a + b > c a + b > c a+b>c 的条件。
- 此时，nums[right] (作为 b b b) 和 nums[left] (作为 a a a) 可以与 maxc 组成三角形。
- 关键：因为数组是排序的，所以 nums[right] (作为 b b b) 与 a a a 之间的任何数 （即 nums[left+1], nums[left+2], ..., nums[right-1]）相加，也必然大于 maxc。
  - 即：nums[left+1] + nums[right] > maxc
  - ...
  - nums[right-1] + nums[right] > maxc
- 因此，对于固定的 nums[right] ( b b b ) 和 固定的 maxc ( c c c ) ，从 left 到 right-1 之间的所有数都可以作为 a a a。
- 这些数的个数是 (right - 1) - left + 1 = right - left。
- 所以，我们直接给结果 ret 加上 right - left。
- right--：加上这些组合后，说明 nums[right] (作为 b b b) 的所有可能性已经统计完毕，我们将 b b b 变小一点（right 左移）继续寻找。
else (即 nums[left] + nums[right] <= maxc)
- 这说明 a + b ≤ c a + b \le c a+b≤c，无法构成三角形。
- 由于 nums[right] 已经是当前子数组中最大的 b b b 了，而 a a a (nums[left]) 又太小了，我们必须增大 a a a 才能使它们的和变大。
- 所以，我们执行 left++。

cpp 复制代码

 int triangleNumber(vector<int>& nums) 
    {
        sort(nums.begin(),nums.end());
        int n = nums.size();
       
        int ret = 0;

        for(int i = n - 1; i > 0; i--)
        { 
            int left = 0;
            int right = i - 1;
            int maxc = nums[i];
            while(left < right)
            {
                if(nums[left] + nums[right] > maxc)
                {
                    ret += right - left;
                    right--;
                }
                else
                {
                    left++;
                }
            }

        }
        return ret;
    }

4. 复杂度分析

时间复杂度 : O ( n 2 ) O(n^2) O(n2)
- 排序需要 O ( n log ⁡ n ) O(n \log n) O(nlogn)。
- 外层循环 O ( n ) O(n) O(n) 次。
- 内层的双指针 while 循环，left 和 right 指针在每次外层循环中最多相遇一次，时间复杂度为 O ( n ) O(n) O(n)。
- 总时间复杂度为 O ( n log ⁡ n ) + O ( n 2 ) = O ( n 2 ) O(n \log n) + O(n^2) = O(n^2) O(nlogn)+O(n2)=O(n2)。
空间复杂度 : O ( log ⁡ n ) O(\log n) O(logn) 或 O ( n ) O(n) O(n)
- 主要取决于排序算法（例如快速排序）所需的递归栈空间。如果只看额外空间，则为 O ( 1 ) O(1) O(1)。

6.查找总价格为目标值的两个商品

1. 问题定义

给定一个已升序排序 的整数数组 price 和一个目标值 target，请在数组中找出两个数，使得它们的和等于 target。

（注意：你的代码实现假设输入的 price 数组已经是排序好的。如果数组未排序，此算法将不成立。）

2. 核心思想

利用数组已排序的特性，我们使用两个指针：

left 指针：指向数组的开头（最小值）。
right 指针：指向数组的末尾（最大值）。

通过比较 price[left] + price[right] (当前和) 与 target 的大小，我们可以有策略地移动指针，逐步缩小搜索范围，直到找到目标。

3. 算法分解

步骤一：初始化指针

cpp 复制代码

int left = 0;
int right = price.size() - 1;

left 指向索引 0，right 指向最后一个元素的索引。

步骤二：循环搜索

cpp 复制代码

while(left < right)
{
    // ...
}

循环持续进行，直到两个指针相遇或错过 (left >= right)，此时表示搜索完所有可能的组合。

步骤三：比较与移动指针（算法核心）

在循环内部，有三种情况：

if(price[left] + price[right] < target)
- 含义：当前的和太小了。
- 策略：我们需要一个更大的和。由于 right 已经指向了当前范围内的最大值，我们只能通过移动 left 指针来尝试一个更大的数。
- 操作：left++
else if(price[left] + price[right] > target)
- 含义：当前的和太大了。
- 策略：我们需要一个更小的和。由于 left 已经指向了当前范围内的最小值，我们只能通过移动 right 指针来尝试一个更小的数。
- 操作：right--
else (即 price[left] + price[right] == target)
- 含义：找到了！当前的 price[left] 和 price[right] 就是我们要找的两个数。
- 操作：break; (跳出循环)

步骤四：返回结果

cpp 复制代码

return {price[left],price[right]};

循环结束后（无论是通过 break 找到的，还是 left >= right 没找到），left 和 right 都停留在最后检查的位置。如果循环是因 break 而停止的，price[left] 和 price[right] 就是那对和为 target 的数。

4. 复杂度分析

时间复杂度 : O ( n ) O(n) O(n)
- left 指针和 right 指针都只向一个方向移动。在最坏的情况下，两个指针共同遍历了整个数组一次。
空间复杂度 : O ( 1 ) O(1) O(1)
- 只使用了 left 和 right 两个额外的整数变量，没有使用额外的数据结构。

cpp 复制代码

 vector<int> twoSum(vector<int>& price, int target) {
        
        int left = 0;
        int right = price.size() - 1;
        while(left < right)
        {
            if(price[left] + price[right] < target)
            {
                left++;
            }
            else if(price[left] + price[right] > target)
            {
                right--;
            }
            else
            {
                break;
            }
        }

        return {price[left],price[right]};
    }

7.三数之和

1. 问题定义

给定一个整数数组 nums，找出所有不重复 的三元组 (nums[i], nums[j], nums[k])，使得 nums[i] + nums[j] + nums[k] == 0。

2. 核心算法：排序 + 双指针

这个问题的 O ( n 3 ) O(n^3) O(n3) 暴力解法很容易想到（三层 for 循环），但效率太低。

你的代码采用了 O ( n 2 ) O(n^2) O(n2) 的高效解法。核心思想是：

排序 (Sorting) ： O ( n log ⁡ n ) O(n \log n) O(nlogn)。排序是使用双指针的前提，它让元素变得有序，也为后续的 "去重" 提供了便利。
双指针 (Two Pointers) ： O ( n 2 ) O(n^2) O(n2)。将三数之和 a + b + c = 0 降维。
- 我们用一层 for 循环来固定第一个数 a (即 nums[i])。
- 问题就转化为在 nums[i] 之后的有序数组中寻找 b 和 c，使得 b + c = -a。
- 这正是我们之前 "两数之和（已排序数组）" 问题，可以用双指针在 O ( n ) O(n) O(n) 时间内解决。

3. 算法分解

步骤一：排序

cpp 复制代码

sort(nums.begin(),nums.end());
int n = nums.size();
vector<vector<int>> vv;

对数组进行升序排序。

步骤二：外层循环（固定 nums[i]）

cpp 复制代码

for(int i = 0; i < n;)
{
    // ...
    // （i 的递增在循环末尾的去重逻辑中处理）
}

这层循环用于遍历并固定第一个数 a ( nums[i] )。

步骤三：剪枝优化

cpp 复制代码

    if(nums[i] > 0)
        break;

这是一个非常关键的剪枝 (Pruning) 操作。

因为数组已经排序，如果 nums[i] (三元组中最小的数) 已经大于 0，那么 nums[i] + nums[left] + nums[right] 必定大于 0。
此时，后续所有的 nums[i] 也都大于 0，不可能再有和为 0 的组合，因此可以直接 break 结束循环。

步骤四：双指针查找 b 和 c

cpp 复制代码

    int left = i + 1;
    int right = n - 1;
    int num = abs(nums[i]); // 相当于 target = -nums[i]
    while(left < right)
    {
        // ...
    }

left 指向 i 之后的第一个元素，right 指向数组末尾。
target 应该是 -nums[i]。
你的代码中 int num = abs(nums[i]); 是正确且巧妙的 ，因为在步骤三的剪枝保证了此时的 nums[i] 必然 ≤ 0 \le 0 ≤0，所以 abs(nums[i]) 就等于 -nums[i]。

步骤五：移动指针（双指针核心）

cpp 复制代码

        if(nums[left]+nums[right] > num)
        {
            right--; // 和太大了，右指针左移
        }
        else if(nums[left]+nums[right] < num)
        {
            left++;  // 和太小了，左指针右移
        }
        else
        {
            // 找到了！
            vv.push_back({nums[i],nums[left],nums[right]});
            // ... (去重)
        }

这部分逻辑与 "两数之和" 完全一致。

步骤六：去重（算法关键）

这是本题最容易出错的地方。你的代码处理了所有三种去重：

找到答案时，对 left 和 right 的去重：
cpp 复制代码
```
else
{
    vv.push_back({nums[i],nums[left],nums[right]});      
    left++;
    right--;
    //去重left 和 right
    while(left < right&&nums[left] == nums[left -1])
    {
        left++;   
    }
    while(left < right&&nums[right] == nums[right+1])
    {
        right--;
    }
}
```
- 当我们找到一组解 {nums[i], nums[left], nums[right]} 后，left 和 right 必须同时移动（left++, right--）才能寻找新的组合。
- 为了防止 left 移动后指向一个重复的元素（例如 [-2, 1, 1, 1, 1, 1] 中找到 {-2, 1, 1} 后，left 不应再次停在 1 上），我们用 while 循环跳过所有与 nums[left - 1] 相同的元素。
- right 指针同理。
外层循环，对 i 的去重：
cpp 复制代码
```
//去重i
i++;
while(i < n&&nums[i] == nums[i - 1])
{
    i++;
}
```
- 这部分放在外层循环的末尾。当 nums[i] 的所有双指针组合（while(left < right)）都查找完毕后，i 需要移动到下一个不相同的元素。
- 这可以防止找到重复的三元组。例如 [-1, -1, 0, 1, 2]，如果不去重 i，i=0 ( nums[i] = -1 ) 会找到 {-1, 0, 1}，i=1 ( nums[i] = -1 ) 也会找到 {-1, 0, 1}，这就重复了。

4. 复杂度分析

时间复杂度 : O ( n 2 ) O(n^2) O(n2)
- sort 排序为 O ( n log ⁡ n ) O(n \log n) O(nlogn)。
- 外层 for 循环为 O ( n ) O(n) O(n)。
- 内层 while 双指针循环为 O ( n ) O(n) O(n)。
- 总时间复杂度为 O ( n log ⁡ n + n 2 ) = O ( n 2 ) O(n \log n + n^2) = O(n^2) O(nlogn+n2)=O(n2)。
空间复杂度 : O ( log ⁡ n ) O(\log n) O(logn) 或 O ( n ) O(n) O(n)
- 主要取决于排序算法（如快速排序）的递归栈空间。如果忽略存储结果的 vv 数组，额外空间复杂度很低。

cpp 复制代码

 vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n = nums.size();
        vector<vector<int>> vv;
        //利用双指针算法
        for(int i = 0; i < n;)
        {
            if(nums[i] > 0)
                break;

            int left = i + 1;
            int right = n - 1;
            int num = abs(nums[i]);
            while(left < right)
            {
                if(nums[left]+nums[right] > num)
                {
                    right--;
                }
                else if(nums[left]+nums[right] < num)
                {
                    left++;    
                }
                else
                {
                    vv.push_back({nums[i],nums[left],nums[right]});         
                    left++;
                    right--;
                    //去重left 和 right
                    while(left < right&&nums[left] == nums[left -1])
                    {
                        left++;  
                    }

                    while(left < right&&nums[right] == nums[right+1])
                    {
                        right--;
                    }

                }
            }
            //去重i
            i++;
            while(i < n&&nums[i] == nums[i - 1])
            {
                i++;
            }
            
        }
        return vv;
    }

8.四数之和

1. 问题定义

给定一个整数数组 nums 和一个目标值 target，找出所有不重复 的四元组 (nums[i], nums[j], nums[k], nums[l])，使得 nums[i] + nums[j] + nums[k] + nums[l] == target。

2. 核心思想：降维（排序 + 双重循环 + 双指针）

这个问题是 "三数之和" 的升级版。我们使用相同的 "降维" 思想：

4Sum 降维 3Sum ：使用一个 for 循环固定第一个数 a (nums[i])。问题转化为在剩余数组中寻找 b + c + d = target - a。
3Sum 降维 2Sum ：再使用一个嵌套的 for 循环固定第二个数 b (nums[j])。问题转化为在剩余数组中寻找 c + d = target - a - b。
2Sum 求解 ：这已经是我们熟悉的 "两数之和" 问题。在 j 之后的有序数组中，使用双指针 （left 和 right）在 O ( n ) O(n) O(n) 时间内寻找 c 和 d。

因此，总的算法结构是 "排序 + 两层for循环 + 一层双指针"。

3. 算法分解

步骤一：排序

cpp 复制代码

sort(nums.begin(),nums.end());
int n = nums.size();
vector<vector<int>> vv;

排序是使用双指针和进行高效去重的前提。

步骤二：固定 a 和 b

cpp 复制代码

for(int i = 0; i < n;)//固定a
{
    int a = nums[i];
    for(int j = i + 1; j < n;)//固定b
    {
        int b = nums[j];
        // ...
    }
}

使用两层 for 循环分别固定前两个数 a 和 b。

步骤三：双指针求解 2Sum

cpp 复制代码

        int left = j + 1;
        int right = n - 1;

        while(left < right)
        {
            // ...
        }

在 j 之后的区间 [j+1, n-1] 内初始化 left 和 right 指针，寻找 c 和 d。

步骤四：目标值计算与溢出处理

cpp 复制代码

            long long tar = (long long)target - a - b;
            int sum = nums[left] + nums[right];

这是一个非常关键 的细节。target - a - b 的计算结果（以及 a+b+c+d 的总和）可能会超出 int 的范围，导致整数溢出。
通过将 target 强制转换为 long long 再进行减法，可以保证 tar 变量能正确存储目标值。
( 注：更安全的方式是将 sum 也定义为 long long sum = (long long)nums[left] + nums[right]; 来防止 c+d 本身溢出，但你代码中的写法在大多数情况下已经解决了最大的溢出风险。 )

步骤五：移动指针

cpp 复制代码

            if(sum > tar)
            {
                right--;
            }
            else if(sum < tar)
            {
                left++;
            }
            else
            {
                // 找到了，处理并去重
            }

这与 "两数之和" 的逻辑完全相同。

步骤六：去重（三层去重）

这是本题的精髓和难点，你的代码正确地处理了所有去重：

left 和 right 去重 (找到答案时)：

cpp 复制代码

        else
        {
            vv.push_back({a,b,nums[left],nums[right]});
            left++;
            right--;
            //left和right去重
            while(left < right && nums[left] == nums[left - 1]) { left++; }
            while(left < right && nums[right] == nums[right + 1]) { right--; }
        }

当找到一组解后，left 和 right 必须跳过所有相同的元素，以避免 (a, b, c, c') 这样的重复。

j 去重 (固定 b 时)：
cpp 复制代码
```
    //j去重
    j++;
    while(j < n && nums[j] == nums[j - 1])
    {
        j++;
    }
```
当 j 的内层 while 循环结束后，j 必须跳过所有与 nums[j-1] 相同的元素，以避免 (a, b, ...) 和 (a, b', ...)（其中 b == b'）导致重复。
i 去重 (固定 a 时)：
cpp 复制代码
```
//i去重
i++;
while(i < n && nums[i] == nums[i - 1])
{
    i++;
}
```
同理，当 i 的内层 for 循环（j 循环）结束后，i 必须跳过所有与 nums[i-1] 相同的元素。

4. 复杂度分析

时间复杂度 : O ( n 3 ) O(n^3) O(n3)
- 排序： O ( n log ⁡ n ) O(n \log n) O(nlogn)。
- i 循环： O ( n ) O(n) O(n)。
- j 循环： O ( n ) O(n) O(n)。
- while 双指针： O ( n ) O(n) O(n)。
- 总时间复杂度为 O ( n log ⁡ n + n 3 ) = O ( n 3 ) O(n \log n + n^3) = O(n^3) O(nlogn+n3)=O(n3)。
空间复杂度 : O ( log ⁡ n ) O(\log n) O(logn) 或 O ( n ) O(n) O(n)
- 主要取决于排序算法（如快速排序）的递归栈空间。如果忽略存储结果的 vv 数组。

cpp 复制代码

 vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        int n = nums.size();
        vector<vector<int>> vv;
        //利用双指针
        for(int i = 0; i < n;)//固定a
        {
            int a = nums[i];
            //利用三数之和
            for(int j = i + 1; j < n;)//固定b
            {
                int b = nums[j];
                int left = j + 1;
                int right = n - 1;

                //双指针
                while(left < right)
                {
                    long long tar = (long long)target - a - b;
                    int sum = nums[left] + nums[right];

                    if(sum > tar)
                    {
                        right--;
                    }
                    else if(sum < tar)
                    {
                        left++;
                    }
                    else
                    {
                        vv.push_back({a,b,nums[left],nums[right]});
                        left++;
                        right--;
                        //left和right去重
                        while(left < right && nums[left] == nums[left - 1])
                        {
                            left++;
                        }

                        while(left < right && nums[right] == nums[right + 1])
                        {
                            right--;
                        }
                    }
                   
                }
                //j去重
                j++;
                while(j < n && nums[j] == nums[j - 1])
                {
                    j++;
                }
               
            }
            //i去重
            i++;
            while(i < n && nums[i] == nums[i - 1])
            {
                i++;
            }

        }
        return vv;
    }

算法练习：双指针专题

目录：

1、移动零

2、复写零

3、快乐数

4、盛最多水的容器

5、有效三角形个数

6.查找总价格为目标值的两个商品

7.三数之和

8.四数之和