C++差分数组（二维）

关于差分数组

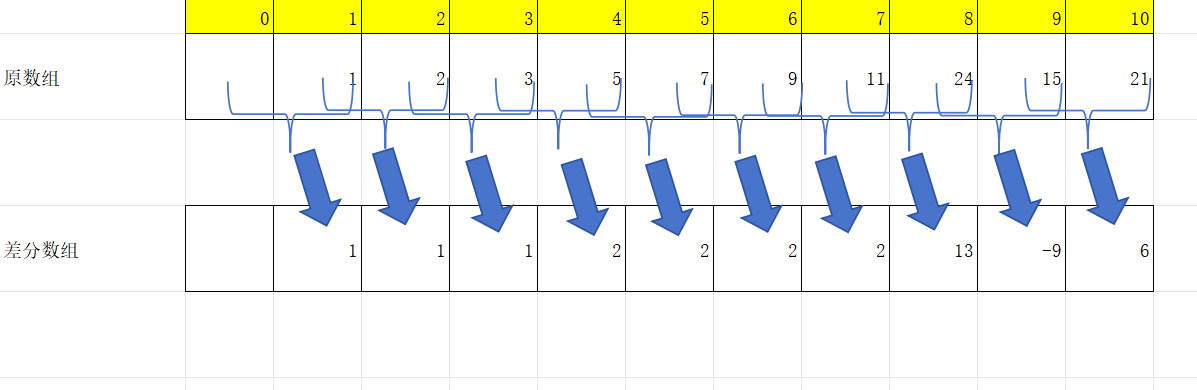
如你所见，差分数组就是表示原数组中相邻数差值的数组，通常只需要给出第一个元素就可以依靠差分数组推出整个原数组。

而且差分数组在变动数组一定范围内的元素时可以减少大量时间，可以很好的避免超时问题（这里描述的有点抽象，能理解就理解吧，尽力了😂）

关于二维差分数组

能理解一维的，二维应该也差不多，就是把一维的扩展到了二维而已，和一维一样，如果想要改变一整个区间（到了二维就应该是矩阵）的所有变量，只需要改变头尾（四个角）的值就可以了

这里是一些简单操作，且看且珍惜

题目

法术叠加

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[10010][10010]={0};
int b[10010][10010]={0};
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>a[i][j];
			b[i][j]=a[i][j]+a[i-1][j-1]-a[i-1][j]-a[i][j-1];
			//^_^
		}
	}
	int t;
	cin>>t;
	while(t--)
	{
		int x1,y1,x2,y2;
		int k;
		cin>>x1>>y1>>x2>>y2>>k;
		b[x1][y1]+=k;
		b[x2+1][y2+1]+=k;
		b[x1][y2+1]-=k;
		b[x2+1][y1]-=k;
		//>_<
	}
	int ma=-1;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			a[i][j]=b[i][j]-a[i-1][j-1]+a[i][j-1]+a[i-1][j];
			ma=max(ma,a[i][j]);
		}
		//_ _
		// ^
	}
	cout<<ma<<endl;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(a[i][j]==ma)
			{
				int sx=i;
				int sy=j;
				int ex=i;
				int ey=j;
				while(a[sx][ey]==ma&&ey<=m)ey++;
				while(a[ex][sy]==ma&&ex<=n)ex++;
				int maex=ex;
				int maey=ey;
				bool ff=false;
				for(ex=maex;ex>=sx;ex--)
				{
					for(int ey=maey;ey>=sy;ey--)
					{
						bool f=true;
						for(int k=sx;k<=ex;k++)
						{
							for(int l=sy;l<=ey;l++)
							{
								if(a[k][l]!=ma)
								{
									f=false;
									break;
								}
							}
							if(f==false)break;
						}
						if(f==true)
						{
							ff=true;
							cout<<sx<<" "<<sy<<" "<<ex<<" "<<ey<<endl;
						}
					}
					if(ff==true)break;
				}
			}
		}
	}
	//                                                _____
	//   ___\  /                     \  \  \  \       |>_<|
	// /|____口--->我>> > )写) ) ) )完}  }  }了}    /[代_码]/
	//  |_ |_                        /  /  /  /       /  /
	
	
	return 0;
}