107.寻找存在的路线
题目描述
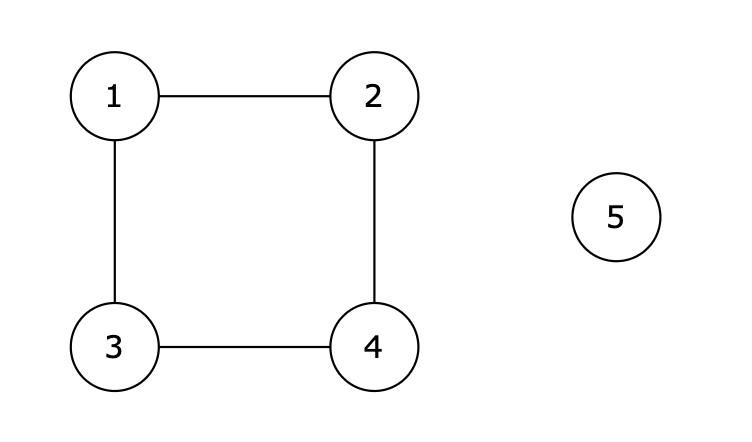
给定一个包含 n 个节点的无向图中,节点编号从 1 到 n (含 1 和 n )。
你的任务是判断是否有一条从节点 source 出发到节点 destination 的路径存在。
输入描述
第一行包含两个正整数 N 和 M,N 代表节点的个数,M 代表边的个数。
后续 M 行,每行两个正整数 s 和 t,代表从节点 s 与节点 t 之间有一条边。
最后一行包含两个正整数,代表起始节点 source 和目标节点 destination。
输出描述
输出一个整数,代表是否存在从节点 source 到节点 destination 的路径。如果存在,输出 1;否则,输出 0。
输入示例
5 4 1 2 1 3 2 4 3 4 1 4输出示例
1提示信息
数据范围:
1 <= M, N <= 100。
原理
并查集 专门用于动态连通性问题:
- 数据结构:father[i]表示节点i的父节点
- 操作 :
- Find:找到集合的根节点
- Union:合并两个集合
- 路径压缩:优化Find操作
代码
java
import java.util.*;
public class Main {
static int sum = 0; // 未使用,冗余变量
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(); // 节点数
int m = scanner.nextInt(); // 边数
// 初始化父节点数组:每个节点初始为自己的父节点
int[] father = new int[n + 1];
for (int i = 1; i <= n; i++) {
father[i] = i; // 每个节点独立成一个集合
}
// 读取M条无向边,并进行并查集合并
for (int i = 0; i < m; i++) {
int u = scanner.nextInt(); // 边起点
int v = scanner.nextInt(); // 边终点
// 无向图:需要双向合并(u→v 和 v→u)
join(u, v, father);
join(v, u, father); // 冗余操作!
}
int source = scanner.nextInt(); // 起始节点
int destination = scanner.nextInt(); // 目标节点
scanner.close();
// 判断source和destination是否在同一连通分量
if (isSame(source, destination, father)) {
System.out.print(1);
} else {
System.out.print(0);
}
}
/**
* 路径压缩的查找操作
* @param u 查找的节点
* @param father 父节点数组
* @return 集合的根节点
*/
public static int find(int u, int[] father) {
// 递归查找根节点,同时进行路径压缩
if (father[u] == u) {
return u; // u是根节点
} else {
return father[u] = find(father[u], father); // 路径压缩
}
}
/**
* 判断两个节点是否在同一集合
* @param u 第一个节点
* @param v 第二个节点
* @param father 父节点数组
* @return 是否在同一集合
*/
public static boolean isSame(int u, int v, int[] father) {
return find(u, father) == find(v, father);
}
/**
* 合并两个集合(Union操作)
* @param u 第一个节点
* @param v 第二个节点
* @param father 父节点数组
*/
public static void join(int u, int v, int[] father) {
u = find(u, father); // 找到u的根
v = find(v, father); // 找到v的根
if (u == v) return; // 已在同一集合,无需合并
father[v] = u; // 简单合并:v的根指向u的根
}
}108.多余的边
题目描述
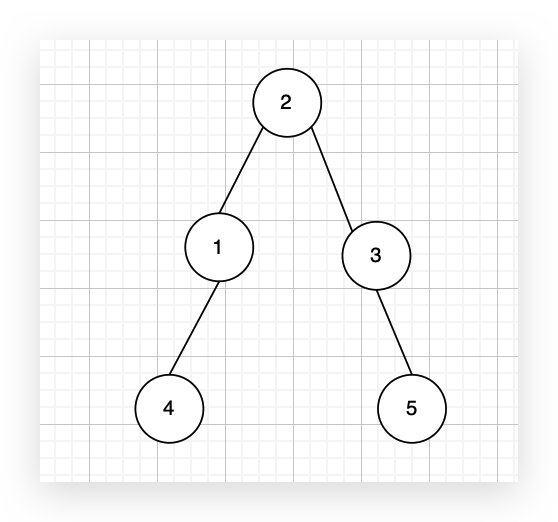
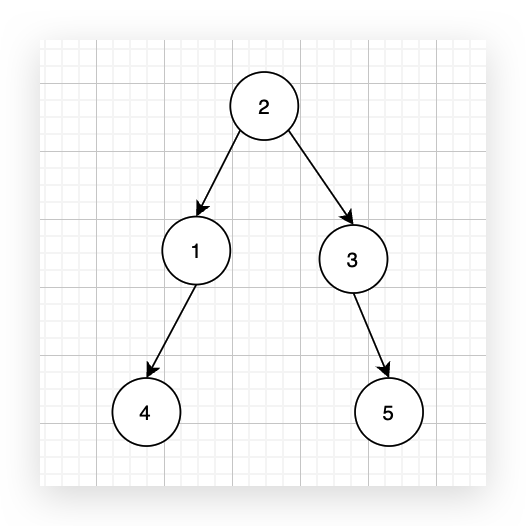
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图,例如如图:
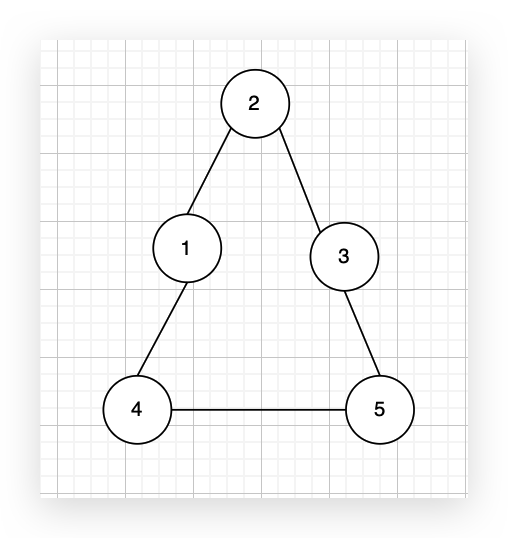
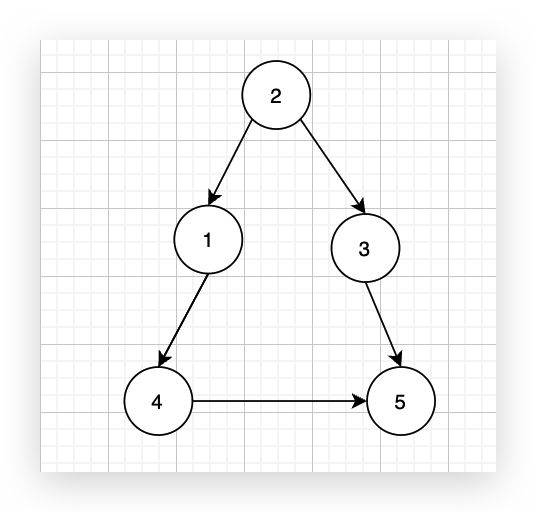
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图:
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
输入描述
第一行包含一个整数 N,表示图的节点个数和边的个数。
后续 N 行,每行包含两个整数 s 和 t,表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案,请删除标准输入中最后出现的那条边。
输入示例
3 1 2 2 3 1 3输出示例
1 3提示信息
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边,所以输出结果为 1 3
数据范围:
1 <= N <= 1000.
原理
核心思想:检测环路边
text
树:N个节点,N-1条边,无环 当前图:N个节点,N条边,必有一环 目标:找到形成环路的"冗余边",删除后变回树并查集处理流程
text
1. 初始化:N个独立集合 2. 按顺序处理N条边: - 如果u,v已在同一集合 → 当前边是冗余边(形成环) - 记录这条边,**但仍合并**(继续构建) 3. 最后记录的冗余边 = 输入中"最后出现"的那条
代码
java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt(); // 节点数=边数=N(含冗余边)
// 创建并查集,处理1~N编号的节点
DisJoint disJoint = new DisJoint(N + 1);
int start = 0, end = 0; // 记录冗余边的两个端点
// 按输入顺序处理N条边
for (int i = 0; i < N; ++i) {
int u = scanner.nextInt(); // 边起点
int v = scanner.nextInt(); // 边终点
// 如果u和v已在同一集合,说明这条边形成环路,是冗余边
if (disJoint.isSame(u, v)) {
start = u; // 记录当前冗余边
end = v;
}
// 无论是否冗余,都合并集合(构建最小生成树)
disJoint.join(u, v);
}
// 输出最后遇到的冗余边
System.out.print(start + " " + end);
}
}
// 并查集实现
class DisJoint {
private int[] father; // 父节点数组
public DisJoint(int N) {
father = new int[N];
// 初始化:每个节点是自己的父节点
for (int i = 0; i < N; ++i) {
father[i] = i;
}
}
// 查找根节点(路径压缩)
public int find(int n) {
return n == father[n] ? n : (father[n] = find(father[n]));
}
// 合并两个集合
public void join(int n, int m) {
n = find(n); // 找n的根
m = find(m); // 找m的根
if (n == m) return; // 同集合,不合并
father[m] = n; // m的根指向n的根
}
// 判断是否同一集合
public boolean isSame(int n, int m) {
return find(n) == find(m);
}
}109.多余的边II
题目描述
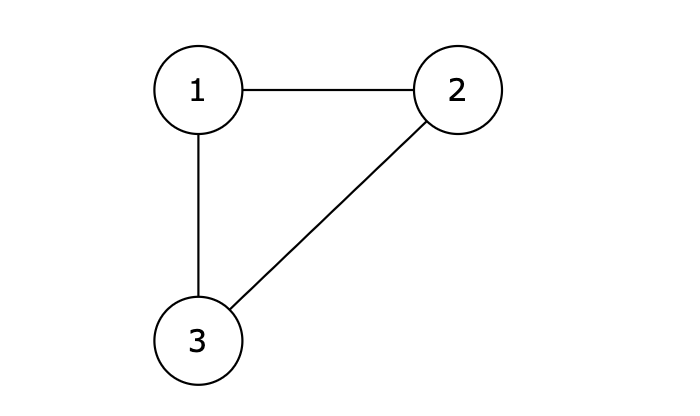
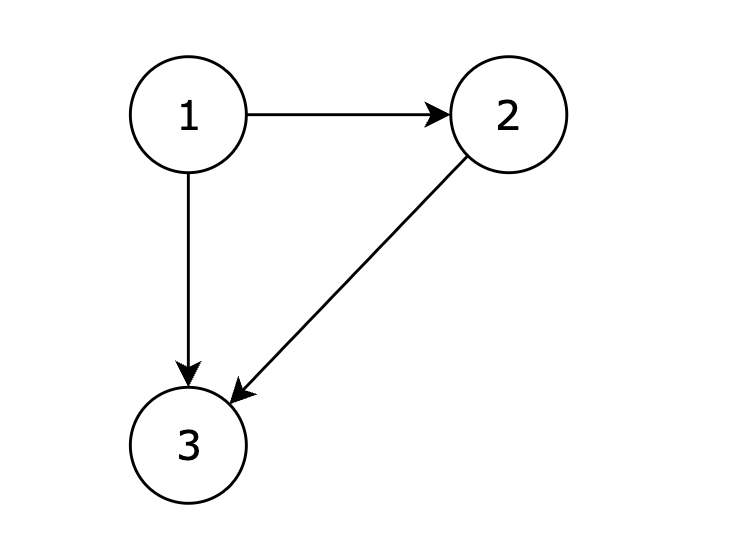
有一种有向树,该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图:
现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:
输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
输入描述
第一行输入一个整数 N,表示有向图中节点和边的个数。
后续 N 行,每行输入两个整数 s 和 t,代表这是 s 节点连接并指向 t 节点的单向边
输出描述
输出一条可以删除的边,若有多条边可以删除,请输出标准输入中最后出现的一条边。
输入示例
3 1 2 1 3 2 3输出示例
2 3提示信息
在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
数据范围:
1 <= N <= 1000.
原理
有向树特性 :每个节点入度≤1 ,总边数=N-1 当前图 :N条边,必有1个入度=2节点 或1条环路边
处理策略
- 统计入度:找到入度=2的节点doubleIn
- 情况1(无入度2) :用并查集按序处理边,最后形成环的边即冗余边
- 情况2(有入度2) :删除指向doubleIn的最后一条边
代码
java
import java.util.*;
public class Main {
// 并查集模板
static class DisJoint {
private int[] father;
public DisJoint(int N) { father = new int[N]; for (int i = 0; i < N; ++i) father[i] = i; }
public int find(int n) { return n == father[n] ? n : (father[n] = find(father[n])); }
public void join(int n, int m) { n = find(n); m = find(m); if (n == m) return; father[m] = n; }
public boolean isSame(int n, int m) { return find(n) == find(m); }
}
// 边类
static class Edge {
int s, t;
public Edge(int s, int t) { this.s = s; this.t = t; }
}
// 节点类:记录入度
static class Node {
int id, in = 0, out = 0;
}
// 找到最后一条形成环的边
public static Edge getRemoveEdge(List<Edge> edges, int n) {
DisJoint disJoint = new DisJoint(n + 1);
Edge ans = new Edge(0, 0);
for (Edge edge : edges) {
if (disJoint.isSame(edge.s, edge.t)) { // 已连通,形成环
ans = edge; // 更新为当前边(最后一条)
}
disJoint.join(edge.s, edge.t); // 继续合并
}
return ans;
}
// 验证删除某边后是否为树
public static boolean isTreeAfterRemoveEdge(Edge excluEdge, List<Edge> edges, int n) {
DisJoint disJoint = new DisJoint(n + 1);
for (Edge edge : edges) {
if (edge.s == excluEdge.s && edge.t == excluEdge.t) continue; // 跳过删除边
if (disJoint.isSame(edge.s, edge.t)) return false; // 仍有环
disJoint.join(edge.s, edge.t);
}
return true;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int N = scanner.nextInt();
List<Edge> edges = new ArrayList<>();
Node[] nodeMap = new Node[N + 1];
// 初始化节点
for (int i = 1; i <= N; i++) nodeMap[i] = new Node();
Integer doubleIn = null; // 记录入度为2的节点
for (int i = 0; i < N; i++) {
int s = scanner.nextInt(), t = scanner.nextInt();
edges.add(new Edge(s, t));
nodeMap[t].in++; // 统计入度
if (nodeMap[t].in == 2) doubleIn = t; // 找到入度为2的节点
}
Edge ans;
if (doubleIn == null) { // 情况1:无入度2节点,用并查集找环边
ans = getRemoveEdge(edges, N);
} else { // 情况2:有入度2节点,删除指向它的最后一条边
List<Edge> excluEdges = new ArrayList<>();
for (Edge edge : edges) {
if (edge.t == doubleIn) excluEdges.add(edge);
if (excluEdges.size() == 2) break;
}
Edge lastEdge = excluEdges.get(1); // 最后一条
if (isTreeAfterRemoveEdge(lastEdge, edges, N)) {
ans = lastEdge;
} else {
ans = excluEdges.get(0); // 第一条
}
}
System.out.print(ans.s + " " + ans.t);
}
}