INT301 Bio-computation 生物计算（神经网络）Pt.3 梯度下降与Sigmoid激活函数

文章目录

• [1.Gradient Descent Rule（梯度下降规则）](#1.Gradient Descent Rule（梯度下降规则）)
• • [1.1 误差曲面（Error Surface）](#1.1 误差曲面（Error Surface）)
  • [1.2 下坡移动](#1.2 下坡移动)
  • [1.3 梯度下降学习算法](#1.3 梯度下降学习算法)
• [2. 增量梯度下降（Incremental Gradient Descent）](#2. 增量梯度下降（Incremental Gradient Descent）)
• [3. 使用 Sigmoid 激活函数的感知机（Sigmoid Perceptrons）](#3. 使用 Sigmoid 激活函数的感知机（Sigmoid Perceptrons）)
• [4. 使用 Sigmoid 激活函数的感知机的增量梯度下降学习算法](#4. 使用 Sigmoid 激活函数的感知机的增量梯度下降学习算法)
• [5. 感知机（Perceptron）和梯度下降（Gradient Descent）的对比](#5. 感知机（Perceptron）和梯度下降（Gradient Descent）的对比)
• • [5.1 误差曲面](#5.1 误差曲面)
  • [5.2 批量学习（Batch learning）和增量学习（Incremental learning）的对比](#5.2 批量学习（Batch learning）和增量学习（Incremental learning）的对比)

1.Gradient Descent Rule（梯度下降规则）

我们上一章学习了感知机规则（Perceptron Rule）：感知机是一种简单的线性分类器，其更新规则是基于错误分类的样本进行权重调整。具体来说，如果一个样本被错误分类，感知机会调整权重以减少错误。

我们上一章提到了感知器的局限性：无法解决线性不可分问题。

为了克服感知机规则的局限性，可以使用梯度下降方法来搜索假设空间（hypothesis space）。梯度下降是一种优化算法，通过迭代更新参数，沿着目标函数梯度的反方向逐步逼近函数的最小值点。

感知机规则基于阈值函数（threshold function），这种函数是不可微分的（not differentiable），因此不能直接使用梯度下降。为了应用梯度下降，需要一个可微分的误差函数。

未阈值线性单元（Unthresholded Linear Unit）：为了使误差函数可微，可以使用未阈值的线性单元。这种单元的输出是输入的线性组合，而不是经过阈值函数处理的结果。

误差函数：一个常用的误差函数是平方误差（squared error），其形式为： E ( w ) = 1 2 ∑ e ( y e − o e ) 2 E(w) = \frac{1}{2} \sum_{e} (y_e - o_e)^2 E(w)=21∑e(ye−oe)2，这里 y e y_e ye是第 e e e个样本的实际输出值。
o e o_e oe是第 e e e个样本的预测输出值（由模型计算得出）。
1 2 \frac{1}{2} 21是一个常数，用于在后续计算梯度时简化表达式，不影响优化过程的结果。

为了理解梯度下降，可以将整个假设空间可视化，包括：

1. 所有可能的权重向量：这些权重向量构成了假设空间的维度。
2. 对应的误差值：每个权重向量都有一个对应的误差值 E E E。

训练过程是沿着最陡峭的方向（即最快速减少误差的方向）来最小化误差 E ( w ) E(w) E(w)，这个方向是与梯度方向相反的： ∇ E ( w ) = [ ∂ E ∂ w 0 , ∂ E ∂ w 1 , ... , ∂ E ∂ w d ] \nabla E(w) = \left[ \frac{\partial E}{\partial w_0}, \frac{\partial E}{\partial w_1}, \ldots, \frac{\partial E}{\partial w_d} \right] ∇E(w)=[∂w0∂E,∂w1∂E,...,∂wd∂E]，

这里， ∇ E ( w ) ∇E(w) ∇E(w)表示损失函数 E ( w ) E(w) E(w)关于权重 w w w的梯度向量。

梯度向量的每个分量是损失函数对每个权重的偏导数，表示损失函数在每个权重方向上的变化率。

根据上述梯度信息，梯度下降的训练规则为： w i = w i − η ∂ E ∂ w i w_i = w_i - \eta \frac{\partial E}{\partial w_i} wi=wi−η∂wi∂E

1.1 误差曲面（Error Surface）

将整个假设空间（hypothesis space）和对应的误差值（E values）可视化可以使用误差曲面。

下图展示了一个误差曲面，

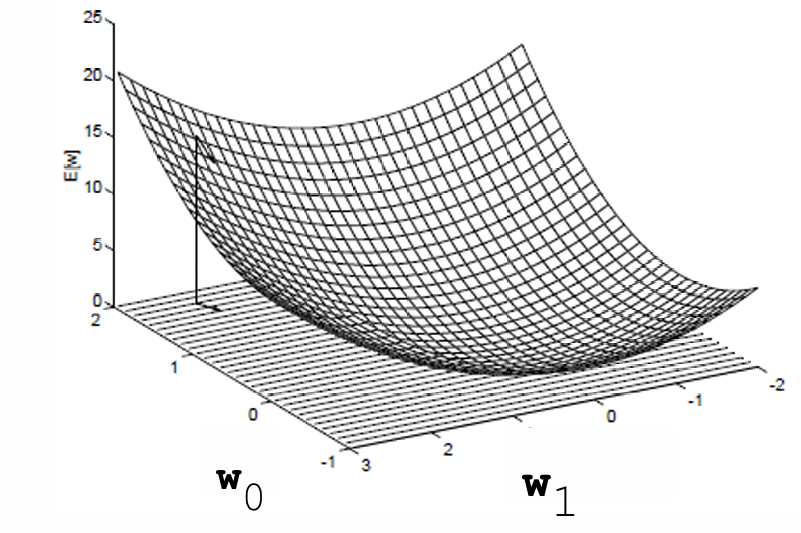
图中的坐标轴 w 0 w_0 w0和 w 1 w_1 w1表示简单线性单元的两个权重的可能值，曲面表示误差函数 E ( w ) E(w) E(w)随着权重 w 0 w_0 w0和 w 1 w_1 w1变化的图形。

误差曲面必须是抛物线形状，并且具有单一的全局最小值。

在误差曲面上，梯度向量指向误差增加最快的方向。因此，梯度的反方向是误差减少最快的方向，梯度下降算法正是沿着这个方向更新参数。

1.2 下坡移动

梯度下降是沿着负导数（negative derivative）的方向更新参数来最小化误差函数 E ( w ) E(w) E(w)。

下图展示了误差函数 E ( w ) E(w) E(w)随 w 1 w_1 w1的变化

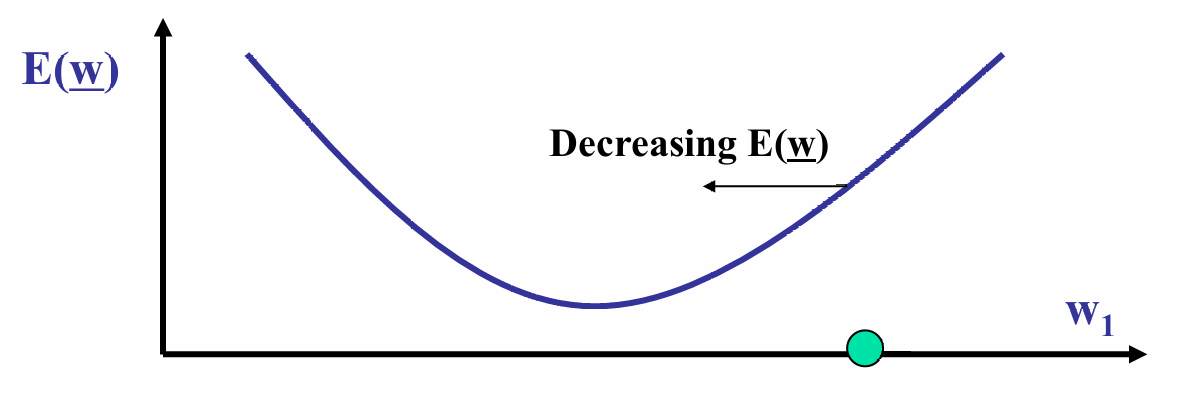
误差函数是凸函数，具有单一全局最小值。

箭头指示了误差函数 E ( w ) E(w) E(w)减少的方向，即沿着抛物线的下坡方向。

下图展示了 d E ( w ) d w 1 \frac{dE(w)}{dw_1} dw1dE(w)随 w 1 w_1 w1的变化：

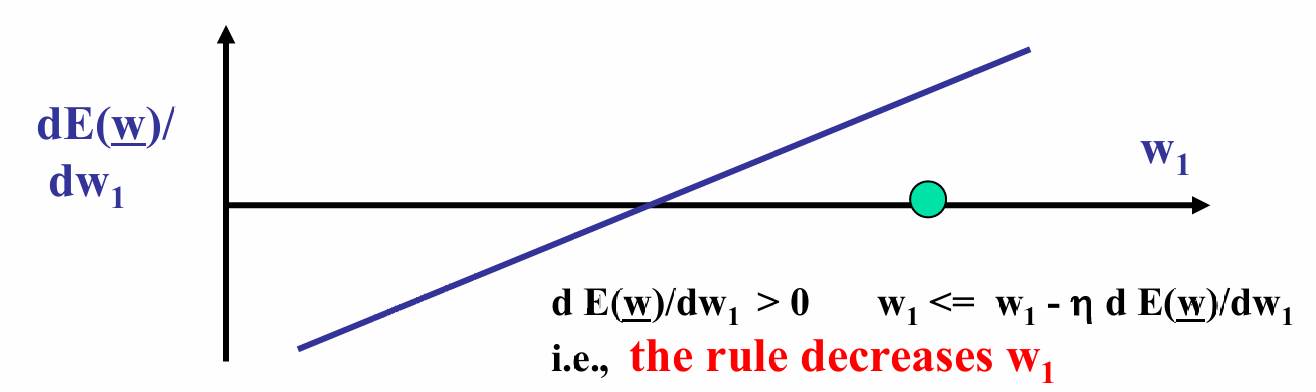
由于误差函数是凸的，导数在最小值点左侧为负，在右侧为正。

现在图中的值导数为正，说明误差函数在增加。

梯度下降的更新规则： w 1 ← w 1 − η d E ( w ) d w 1 w_1 \leftarrow w_1 - \eta \frac{dE(w)}{dw_1} w1←w1−ηdw1dE(w)，即沿着导数的负方向（即下坡方向）更新 w 1 w_1 w1 ，其中 η η η是学习率。

对于另一边。

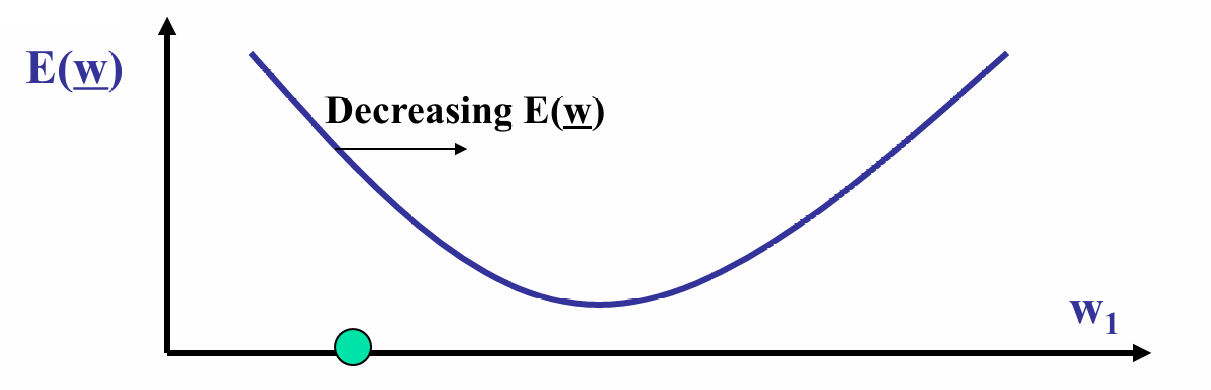
箭头指示了误差函数 E ( w ) E(w) E(w)减少的方向，即沿着抛物线的下坡方向。

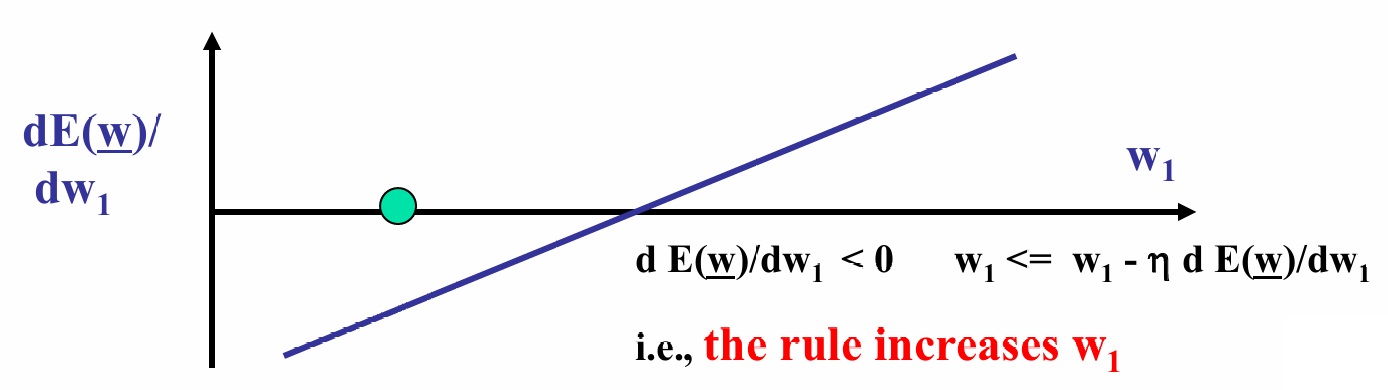
现在图中的值导数为负，说明误差函数在减少。

我们现在展示三维的图。

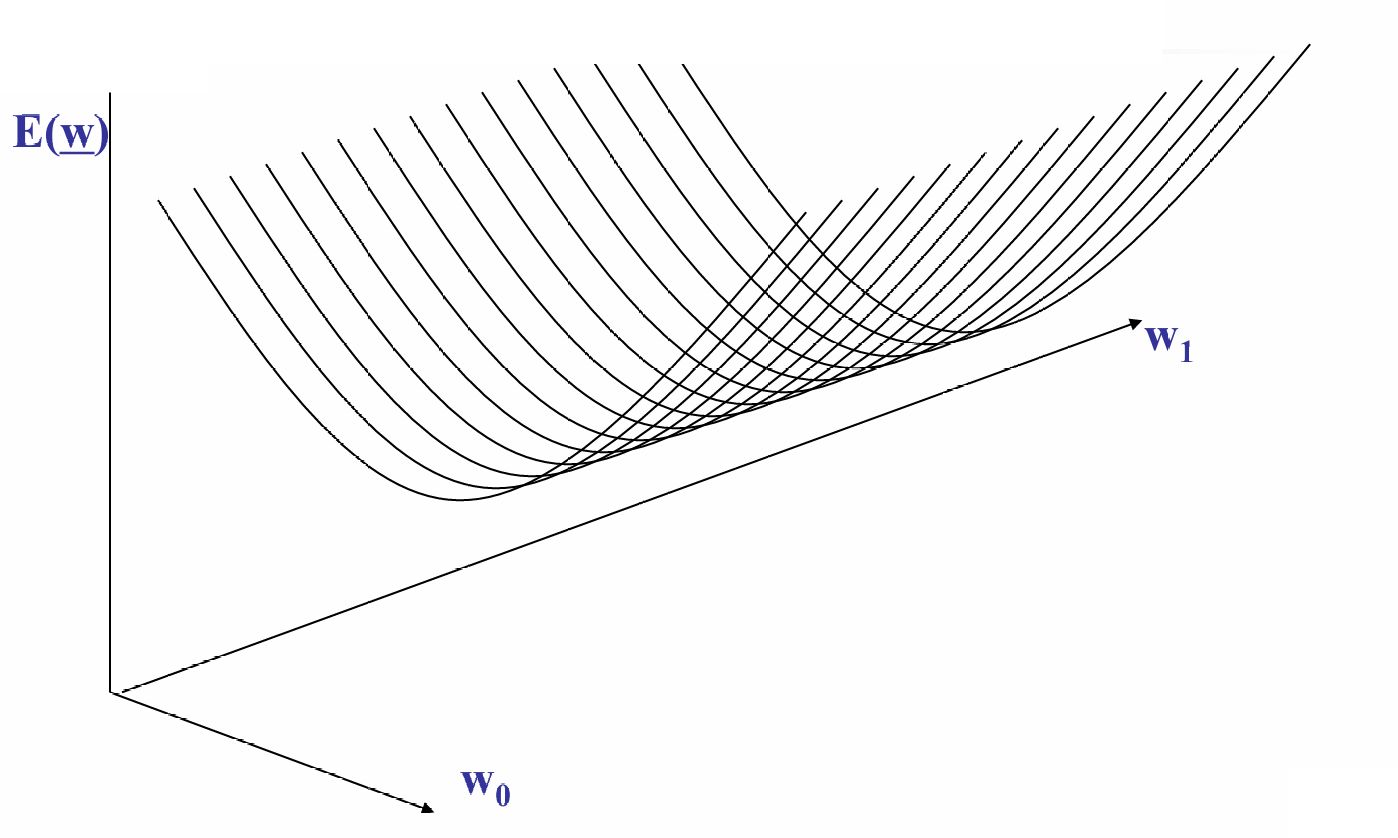
图中的曲面表示了误差函数 E ( w ) E(w) E(w)随参数 w 0 w_0 w0和 w 1 w_1 w1变化的情况。

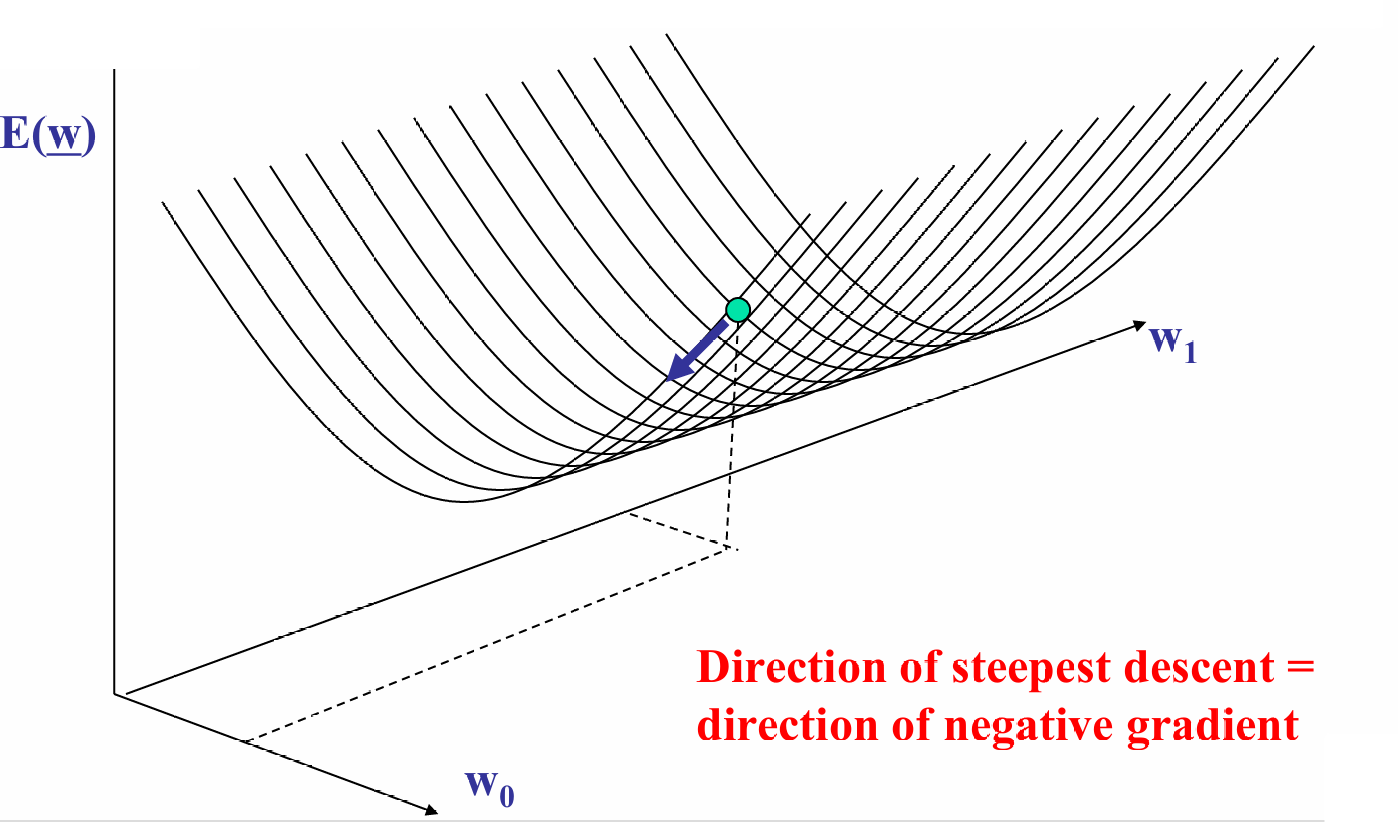
假设从曲面上的某个点开始。

我们在每个点上，计算误差函数的梯度（即偏导数），梯度指向误差增加最快的方向。

我们沿着梯度的反方向（即最陡峭下降方向）更新参数，逐步减少误差。

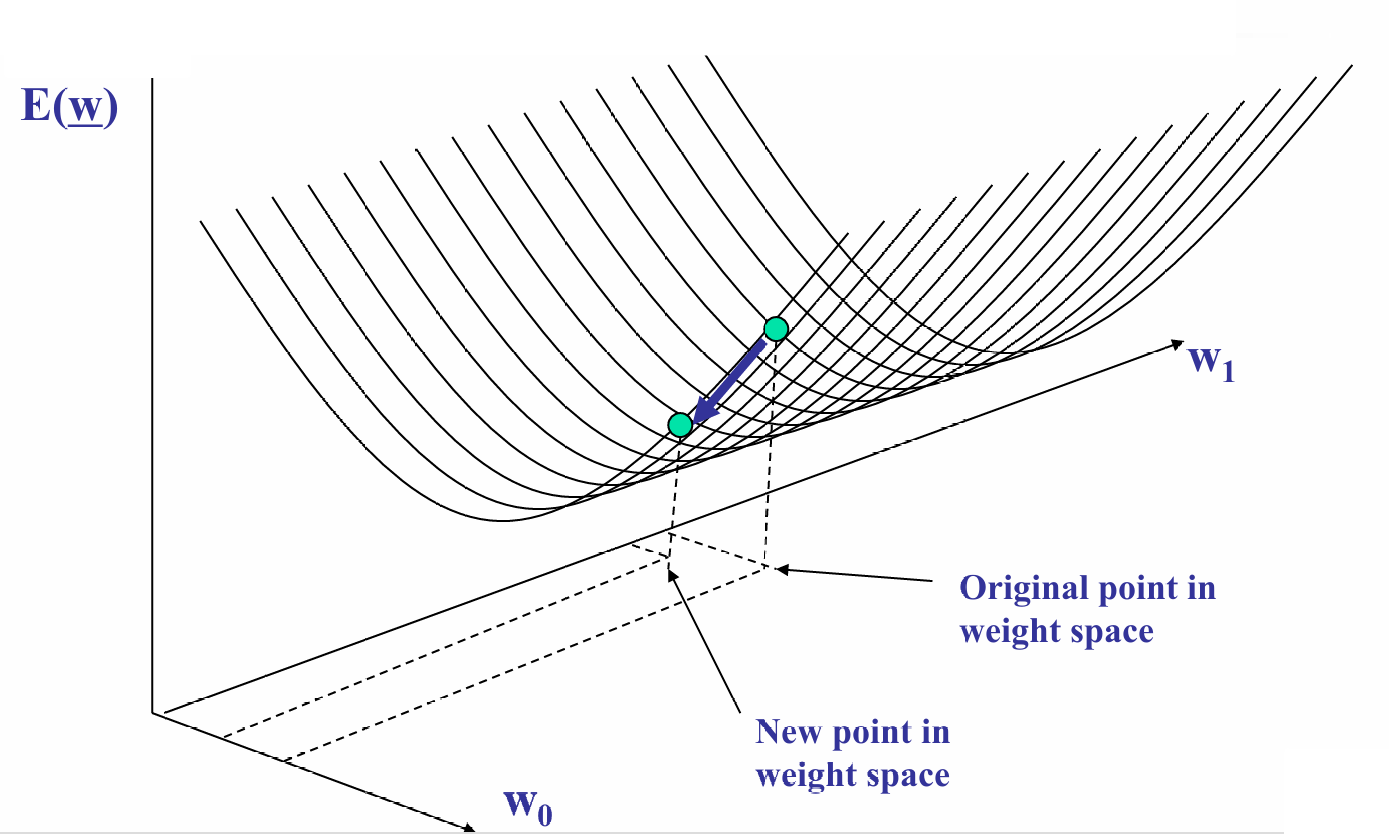
我们的更新过程是不断迭代的。

我们再更新一次后就会获得一个新的点，我们会继续计算当前点的梯度，沿着梯度的反方向（最陡下降方向）更新权重，移动到新的点。

1.3 梯度下降学习算法

我们先推导一遍公式：
∂ E ∂ w = ∂ ∂ w i ( 1 2 ∑ e ( y e − o e ) 2 ) \frac{\partial E}{\partial w} = \frac{\partial}{\partial w_i} \left( \frac{1}{2} \sum_e (y_e - o_e)^2 \right) ∂w∂E=∂wi∂(21∑e(ye−oe)2)
= 1 2 ∑ e ∂ ∂ w i ( y e − o e ) 2 = \frac{1}{2} \sum_e \frac{\partial}{\partial w_i} (y_e - o_e)^2 =21∑e∂wi∂(ye−oe)2
= 1 2 ∑ e 2 ( y e − o e ) ∂ ( y e − o e ) ∂ w i = \frac{1}{2} \sum_e 2(y_e - o_e) \frac{\partial (y_e - o_e)}{\partial w_i} =21∑e2(ye−oe)∂wi∂(ye−oe)
= ∑ e ( y e − o e ) ∂ ( y e − w i ) ⋅ x i e ∂ w i = \sum_e (y_e - o_e) \frac{\partial (y_e - w_i)\cdot x_{ie}}{\partial w_i} =∑e(ye−oe)∂wi∂(ye−wi)⋅xie
= ∑ e ( y e − o e ) ( − x i e ) = \sum_e (y_e - o_e) (-x_{ie}) =∑e(ye−oe)(−xie)

其中 x i e x_{ie} xie表示第 e e e个样本的第 i i i个特征值。

使用上述梯度，权重更新规则为： w i = w i + η ∑ e ( y e − o e ) x i e w_i = w_i + \eta \sum_{e} (y_e - o_e) x_{ie} wi=wi+η∑e(ye−oe)xie

我们现在了解算法后，由以下步骤进行训练：

1. 初始化（Initialization）：
   样本集： { ( x e , y e ) } e = 1 N \{(x_e, y_e)\}_{e=1}^{N} {(xe,ye)}e=1N其中 x e x_e xe是输入特征， y e y_e ye是对应的输出标签。
   初始权重： w i w_i wi设置为小的随机值。
   学习率参数： η η η，控制每次更新的步长。
2. 重复执行（Repeat）：
   对于每个训练样本 ( x e , y e ) (x_e, y_e) (xe,ye)：
   计算模型的预测输出 o e o_e oe: o e = ∑ i = 0 d w i x i e o_e = \sum_{i=0}^{d} w_i x_{ie} oe=∑i=0dwixie其中 d d d是权重的数量， x i e x_{ie} xie是第 e e e个样本的第 i i i个特征值。
   如果感知机没有正确响应（即预测输出 o e o_e oe与实际输出 y e y_e ye不符），计算权重的修正量 Δ w i Δw_i Δwi： Δ w i = Δ w i + η ( y e − o e ) x i e \Delta w_i = \Delta w_i + \eta (y_e - o_e) x_{ie} Δwi=Δwi+η(ye−oe)xie
   使用所有样本累积的误差更新权重： w i = w i + Δ w i w_i = w_i + \Delta w_i wi=wi+Δwi，这一步也是梯度下降规则。
   重复上述过程，直到满足某个终止条件（如达到最大迭代次数、误差低于某个阈值或权重更新量非常小）。

我们现在给出一个使用梯度下降算法更新感知机权重的示例。

现在感知机有两个输入以及三个权重 w 1 = 0.5 w_1 = 0.5 w1=0.5， w 2 = 0.3 w_2 = 0.3 w2=0.3， w 0 = − 1 w_0 = -1 w0=−1。学习率被设置为 η = 1 η=1 η=1。

现在给出输入 x 1 = 2 ， x 2 = 1 x_1=2，x_2=1 x1=2，x2=1，期望输出 y = 0 y=0 y=0。

计算感知机的网络输出 o o o： o = w 0 + w 1 ⋅ x 1 + w 2 ⋅ x 2 o = w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 o=w0+w1⋅x1+w2⋅x2
o = − 1 + 0.5 ⋅ 2 + 0.3 ⋅ 1 o = -1 + 0.5 \cdot 2 + 0.3 \cdot 1 o=−1+0.5⋅2+0.3⋅1
o = − 1 + 1 + 0.3 o = -1 + 1 + 0.3 o=−1+1+0.3
o = 0.3 o = 0.3 o=0.3

由于感知机的输出 o = 0.3 o=0.3 o=0.3与期望输出 y = 0 y=0 y=0不符，需要更新权重。权重更新的计算如下：

对于 w 1 w_1 w1:
Δ w 1 = η ⋅ ( y − o ) ⋅ x 1 \Delta w_1 = \eta \cdot (y - o) \cdot x_1 Δw1=η⋅(y−o)⋅x1
Δ w 1 = 1 ⋅ ( 0 − 0.3 ) ⋅ 2 \Delta w_1 = 1 \cdot (0 - 0.3) \cdot 2 Δw1=1⋅(0−0.3)⋅2
Δ w 1 = − 0.6 \Delta w_1 = -0.6 Δw1=−0.6

对于 w 2 w_2 w2:
Δ w 2 = η ⋅ ( y − o ) ⋅ x 2 \Delta w_2 = \eta \cdot (y - o) \cdot x_2 Δw2=η⋅(y−o)⋅x2
Δ w 2 = 1 ⋅ ( 0 − 0.3 ) ⋅ 1 \Delta w_2 = 1 \cdot (0 - 0.3) \cdot 1 Δw2=1⋅(0−0.3)⋅1
Δ w 2 = − 0.3 \Delta w_2 = -0.3 Δw2=−0.3

对于 w 0 w_0 w0：
Δ w 0 = η ⋅ ( y − o ) ⋅ 1 \Delta w_0 = \eta \cdot (y - o) \cdot 1 Δw0=η⋅(y−o)⋅1
Δ w 0 = 1 ⋅ ( 0 − 0.3 ) ⋅ 1 \Delta w_0 = 1 \cdot (0 - 0.3) \cdot 1 Δw0=1⋅(0−0.3)⋅1
Δ w 0 = − 0.3 \Delta w_0 = -0.3 Δw0=−0.3

现在给出另一组输入 x 1 = 1 ， x 2 = 2 x_1=1，x_2=2 x1=1，x2=2，期望输出 y = 1 y=1 y=1。

计算感知机的网络输出 o o o： o = w 0 + w 1 ⋅ x 1 + w 2 ⋅ x 2 o = w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 o=w0+w1⋅x1+w2⋅x2
o = − 1 + 0.5 ⋅ 1 + 0.3 ⋅ 2 o = -1 + 0.5 \cdot 1 + 0.3 \cdot 2 o=−1+0.5⋅1+0.3⋅2
o = − 1 + 0.5 + 0.6 o = -1 + 0.5 + 0.6 o=−1+0.5+0.6
o = 0.1 o = 0.1 o=0.1

由于感知机的输出 o = 0.3 o=0.3 o=0.3与期望输出 y = 0 y=0 y=0不符，需要更新权重。权重更新的计算如下：

对于 w 1 w_1 w1:
Δ w 1 = Δ w 1 + η ⋅ ( y − o ) ⋅ x 1 \Delta w_1 = \Delta w_1+\eta \cdot (y - o) \cdot x_1 Δw1=Δw1+η⋅(y−o)⋅x1
Δ w 1 = − 0.6 + 1 ⋅ ( 1 − 0.1 ) ⋅ 1 \Delta w_1 =-0.6+ 1 \cdot (1 - 0.1) \cdot 1 Δw1=−0.6+1⋅(1−0.1)⋅1
Δ w 1 = 0.3 \Delta w_1 = 0.3 Δw1=0.3

对于 w 2 w_2 w2:
Δ w 2 = Δ w 2 + η ⋅ ( y − o ) ⋅ x 2 \Delta w_2 = \Delta w_2+\eta \cdot (y - o) \cdot x_2 Δw2=Δw2+η⋅(y−o)⋅x2
Δ w 2 = − 0.3 + 1 ⋅ ( 1 − 0.1 ) ⋅ 2 \Delta w_2 = -0.3+1 \cdot (1 - 0.1) \cdot 2 Δw2=−0.3+1⋅(1−0.1)⋅2
Δ w 2 = 1.5 \Delta w_2 = 1.5 Δw2=1.5

对于 w 0 w_0 w0：
Δ w 0 = Δ w 3 + η ⋅ ( y − o ) ⋅ 1 \Delta w_0 = \Delta w_3+\eta \cdot (y - o) \cdot 1 Δw0=Δw3+η⋅(y−o)⋅1
Δ w 0 = − 0.3 + 1 ⋅ ( 1 − 0.1 ) ⋅ 1 \Delta w_0 = - 0.3+ 1 \cdot (1 - 0.1) \cdot 1 Δw0=−0.3+1⋅(1−0.1)⋅1
Δ w 0 = 0.6 \Delta w_0 =0.6 Δw0=0.6

由于现在没有更多的例子了，因此我们使用所有样本累积的误差更新权重：
w 1 = 0.5 + 0.3 = 0.8 w_1=0.5+0.3=0.8 w1=0.5+0.3=0.8
w 2 = 0.3 + 1.5 = 1.8 w_2=0.3 + 1.5 = 1.8 w2=0.3+1.5=1.8
w 0 = − 1 + 0.6 = − 0.4 w_0=- 1 + 0.6 = -0.4 w0=−1+0.6=−0.4

2. 增量梯度下降（Incremental Gradient Descent）

传统梯度下降算法在实践中遇到的两个主要困难：

1. 收敛速度慢：传统梯度下降算法在每次迭代时需要计算整个训练集上的误差，这在数据量很大时会导致每次更新权重都非常耗时，从而使得算法收敛速度变慢。
2. 局部最小值问题：如果误差曲面存在多个局部最小值，传统梯度下降算法不能保证找到全局最小值，它可能会收敛到一个局部最小值，这可能不是最优解。

为了解决这些问题，增量梯度下降算法被提出。与传统梯度下降算法不同，增量梯度下降算法不是在计算了所有样本的累积误差后才更新权重，而是在处理每个训练样本后立即更新权重。这种更新方式称为增量更新，因为它是逐个样本进行的，每次只基于一个样本的误差来更新权重。

所以公式都与前面一致：

权重更新规则为 w i = w i + η ( y e − o e ) x i e w_i = w_i + \eta (y_e - o_e) x_{ie} wi=wi+η(ye−oe)xie。

预测输出为 o e = ∑ i = 0 d w i x i e o_e = \sum_{i=0}^{d} w_i x_{ie} oe=∑i=0dwixie。

步骤如下：

1. 初始化（Initialization）：
   样本集： { ( x e , y e ) } e = 1 N \{(x_e, y_e)\}_{e=1}^{N} {(xe,ye)}e=1N其中 x e x_e xe是输入特征， y e y_e ye是对应的输出标签。
   初始权重： w i w_i wi设置为小的随机值。
   学习率参数： η η η。
2. 重复执行（Repeat）：
   对于每个训练样本 ( x e , y e ) (x_e, y_e) (xe,ye)：
   计算模型的预测输出 o e o_e oe: o e = ∑ i = 0 d w i x i e o_e = \sum_{i=0}^{d} w_i x_{ie} oe=∑i=0dwixie其中 d d d是权重的数量， x i e x_{ie} xie是第 e e e个样本的第 i i i个特征值。
   如果感知机没有正确响应（即预测输出 o e o_e oe与实际输出 y e y_e ye不符），则根据以下规则更新权重： w i = w i + η ( y e − o e ) x i e w_i = w_i + \eta (y_e - o_e) x_{ie} wi=wi+η(ye−oe)xie
   重复上述过程，直到满足某个终止条件（如达到最大迭代次数、误差低于某个阈值或权重更新量非常小）。

3. 使用 Sigmoid 激活函数的感知机（Sigmoid Perceptrons）

传统的单层感知机使用阈值或线性激活函数，这些函数限制了感知机的泛化能力，使其难以处理复杂的非线性问题。

由于这些限制，简单的感知机不能很好地推广到更强大的学习机制，如多层神经网络。

为了克服这些局限性，开发了使用 Sigmoid 激活函数的单层感知机。

Sigmoid 激活函数能够引入非线性特性，使得感知机能够学习和模拟更复杂的函数，从而提高其泛化能力。
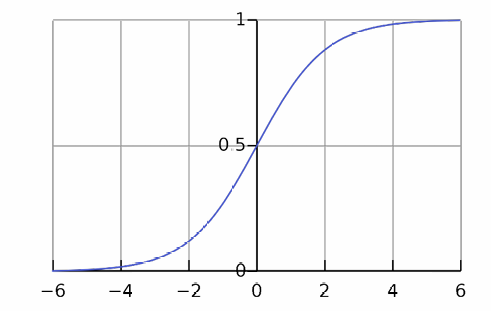
o = σ ( S ) = 1 1 + e − S o = \sigma(S) = \frac{1}{1 + e^{-S}} o=σ(S)=1+e−S1，其中， S S S是感知机的加权输入和，计算公式为： S = ∑ i = 0 d w i x i S = \sum_{i=0}^{d} w_i x_i S=∑i=0dwixi，这里， d d d是权重的数量（包括偏置项）， w i w_i wi是第 i i i个权重， x i x_i xi是第 i i i个输入特征。

下图展示了 Sigmoid 函数的曲线，显示了其输出范围在 0 到 1 之间，并且具有 S 形曲线的特征。

权重更新的梯度下降规则： w i = w i − η ∂ E ∂ w i w_i = w_i - \eta \frac{\partial E}{\partial w_i} wi=wi−η∂wi∂E

由于使用了 Sigmoid 激活函数，误差导数 ∂ E ∂ w i \frac{\partial E}{\partial w_i} ∂wi∂E计算方式会有所不同。具体步骤如下： ∂ E ∂ w i = ∂ ∂ w i ( 1 2 ∑ e ( y e − o e ) 2 ) \frac{\partial E}{\partial w_i} = \frac{\partial}{\partial w_i} \left( \frac{1}{2} \sum_e (y_e - o_e)^2 \right) ∂wi∂E=∂wi∂(21∑e(ye−oe)2)
= 1 2 ∑ e ∂ ∂ w i ( y e − o e ) 2 = \frac{1}{2} \sum_e \frac{\partial}{\partial w_i} (y_e - o_e)^2 =21∑e∂wi∂(ye−oe)2
= ∑ e ( y e − o e ) ∂ ( y e − o e ) ∂ w i = \sum_e (y_e - o_e) \frac{\partial (y_e-o_e)}{\partial w_i} =∑e(ye−oe)∂wi∂(ye−oe)
= ∑ e ( y e − o e ) ∂ ( y e − σ ( S ) ) ∂ w i = \sum_e (y_e - o_e) \frac{\partial (y_e-\sigma(S))}{\partial w_i} =∑e(ye−oe)∂wi∂(ye−σ(S))
∑ e ( y e − o e ) σ ′ ( S ) ( − x i e ) \sum_e (y_e - o_e) \sigma'(S) (-x_{ie}) ∑e(ye−oe)σ′(S)(−xie)

其中 x i e x_{ie} xie表示第 e e e个样本的第 i i i个特征值。

我们计算Sigmoid 函数的导数： σ ′ ( S ) = σ ( S ) ( 1 − σ ( S ) ) \sigma'(S) = \sigma(S)(1 - \sigma(S)) σ′(S)=σ(S)(1−σ(S))

步骤如下：

1. 初始化（Initialization）：
   样本集： { ( x e , y e ) } e = 1 N \{(x_e, y_e)\}_{e=1}^{N} {(xe,ye)}e=1N其中 x e x_e xe是输入特征， y e y_e ye是对应的输出标签。
   初始权重： w i w_i wi设置为小的随机值。
   学习率参数： η η η。
2. 重复执行（Repeat）：
   对于每个训练样本 ( x e , y e ) (x_e, y_e) (xe,ye)：
   计算模型的预测输出 o o o: o = σ ( S ) o = \sigma(S) o=σ(S)其中 S S S是加权输入和 S = ∑ i = 0 d w i x i e S = \sum_{i=0}^{d} w_i x_{ie} S=∑i=0dwixie
   如果感知机没有正确响应（即预测输出 o e o_e oe与实际输出 y e y_e ye不符），则根据以下规则更新权重： Δ w i = Δ w i + η ( y e − o e ) σ ( S ) ( 1 − σ ( S ) ) x i e \Delta w_i = \Delta w_i + \eta (y_e - o_e) \sigma(S)(1- \sigma(S))x_{ie} Δwi=Δwi+η(ye−oe)σ(S)(1−σ(S))xie
   使用所有样本累积的误差更新权重： w i = w i + Δ w i w_i = w_i + \Delta w_i wi=wi+Δwi
   重复上述过程，直到满足某个终止条件（如达到最大迭代次数、误差低于某个阈值或权重更新量非常小）。

我们现在给出例子。

现在感知机有两个输入以及三个权重 w 1 = 0.5 w_1 = 0.5 w1=0.5， w 2 = 0.3 w_2 = 0.3 w2=0.3， w 0 = − 1 w_0 = -1 w0=−1。学习率被设置为 η = 1 η=1 η=1。

现在给出输入 x 1 = 2 ， x 2 = 1 x_1=2，x_2=1 x1=2，x2=1，期望输出 y = 0 y=0 y=0。

计算感知机的加权输入和 S S S： S = w 0 + w 1 ⋅ x 1 + w 2 ⋅ x 2 S = w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 S=w0+w1⋅x1+w2⋅x2
S = − 1 + 0.5 ⋅ 2 + 0.3 ⋅ 1 S = -1 + 0.5 \cdot 2 + 0.3 \cdot 1 S=−1+0.5⋅2+0.3⋅1
S = − 1 + 1 + 0.3 S = -1 + 1 + 0.3 S=−1+1+0.3
S = 0.3 S = 0.3 S=0.3

然后，使用 Sigmoid 函数计算输出 o o o： o = σ ( S ) = 1 1 + e − S o = \sigma(S) = \frac{1}{1 + e^{-S}} o=σ(S)=1+e−S1
o = σ ( 0.3 ) ≈ 0.5744 o = \sigma(0.3) \approx 0.5744 o=σ(0.3)≈0.5744

由于感知机的输出 o = 0.5744 o=0.5744 o=0.5744与期望输出 y = 0 不符 y=0 不符 y=0不符，需要更新权重，需要更新权重。权重更新的计算如下：
Δ w 0 = ( y − o ) σ ( S ) ( 1 − σ ( S ) ) ⋅ x 0 e \Delta w_0 = (y - o) \sigma(S)(1- \sigma(S)) \cdot x_{0e} Δw0=(y−o)σ(S)(1−σ(S))⋅x0e
Δ w 0 = ( 0 − 0.5744 ) ⋅ 0.5744 ⋅ ( 1 − 0.5744 ) ⋅ 1 = − 0.1404 \Delta w_0 = (0 - 0.5744) \cdot 0.5744 \cdot ( 1 -0.5744 ) \cdot 1 = -0.1404 Δw0=(0−0.5744)⋅0.5744⋅(1−0.5744)⋅1=−0.1404

Δ w 1 = ( y − o ) σ ( S ) ( 1 − σ ( S ) ) ⋅ x 1 e \Delta w_1 = (y - o) \sigma(S)(1- \sigma(S)) \cdot x_{1e} Δw1=(y−o)σ(S)(1−σ(S))⋅x1e
Δ w 1 = ( 0 − 0.5744 ) ⋅ 0.5744 ⋅ ( 1 − 0.5744 ) ⋅ 2 = − 0.2808 \Delta w_1 = (0 - 0.5744) \cdot 0.5744 \cdot ( 1 -0.5744 ) \cdot 2 = -0.2808 Δw1=(0−0.5744)⋅0.5744⋅(1−0.5744)⋅2=−0.2808

Δ w 2 = ( y − o ) ⋅ σ ( S ) ( 1 − σ ( S ) ) ⋅ x 2 e \Delta w_2 = (y - o) \cdot \sigma(S)(1- \sigma(S)) \cdot x_{2e} Δw2=(y−o)⋅σ(S)(1−σ(S))⋅x2e
Δ w 2 = ( 0 − 0.5744 ) ⋅ 0.5744 ⋅ ( 1 − 0.5744 ) ⋅ 1 = − 0.1404 \Delta w_2 = (0 - 0.5744) \cdot 0.5744 \cdot ( 1 -0.5744 ) \cdot 1 = -0.1404 Δw2=(0−0.5744)⋅0.5744⋅(1−0.5744)⋅1=−0.1404

现在给出另一组输入 x 1 = 1 ， x 2 = 2 x_1=1，x_2=2 x1=1，x2=2，期望输出 y = 1 y=1 y=1。

计算感知机的加权输入和 S S S： S = w 0 + w 1 ⋅ x 1 + w 2 ⋅ x 2 S = w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 S=w0+w1⋅x1+w2⋅x2
S = − 1 + 0.5 ⋅ 1 + 0.3 ⋅ 2 S = -1 + 0.5 \cdot 1 + 0.3 \cdot 2 S=−1+0.5⋅1+0.3⋅2
S = − 1 + 0.5 + 0.6 S = -1 + 0.5 + 0.6 S=−1+0.5+0.6
S = 0.1 S = 0.1 S=0.1

然后，使用 Sigmoid 函数计算输出 o o o： o = σ ( S ) = 1 1 + e − S o = \sigma(S) = \frac{1}{1 + e^{-S}} o=σ(S)=1+e−S1
o = σ ( 0.1 ) ≈ 0.525 o = \sigma(0.1) \approx 0.525 o=σ(0.1)≈0.525

由于感知机的输出 o = 0.5744 o=0.5744 o=0.5744与期望输出 y = 0 不符 y=0 不符 y=0不符，需要更新权重，需要更新权重。权重更新的计算如下：
Δ w 0 = Δ w 0 + ( y − o ) σ ( S ) ( 1 − σ ( S ) ) ⋅ x 0 e \Delta w_0 = \Delta w_0+(y - o) \sigma(S)(1- \sigma(S)) \cdot x_{0e} Δw0=Δw0+(y−o)σ(S)(1−σ(S))⋅x0e
Δ w 0 = − 0.1404 + ( 1 − 0.525 ) ∗ 0.525 ∗ ( 1 − 0.525 ) ∗ 1 = − 0.0219 \Delta w_0 =- 0.1404 + ( 1 - 0.525 ) * 0.525 * ( 1 - 0.525 ) * 1 = -0.0219 Δw0=−0.1404+(1−0.525)∗0.525∗(1−0.525)∗1=−0.0219

Δ w 1 = Δ w 1 + ( y − o ) σ ( S ) ( 1 − σ ( S ) ) ⋅ x 1 e \Delta w_1 = \Delta w_1+(y - o) \sigma(S)(1- \sigma(S)) \cdot x_{1e} Δw1=Δw1+(y−o)σ(S)(1−σ(S))⋅x1e
Δ w 1 = − 0.2808 + ( 1 − 0.525 ) ∗ 0.525 ∗ ( 1 − 0.525 ) ∗ 1 = − 0.1623 \Delta w_1 = - 0.2808 + ( 1 - 0.525 ) * 0.525 * ( 1 - 0.525 ) * 1 = -0.1623 Δw1=−0.2808+(1−0.525)∗0.525∗(1−0.525)∗1=−0.1623

Δ w 2 = Δ w 2 + ( y − o ) ⋅ σ ( S ) ( 1 − σ ( S ) ) ⋅ x 2 e \Delta w_2 = \Delta w_2+(y - o) \cdot \sigma(S)(1- \sigma(S)) \cdot x_{2e} Δw2=Δw2+(y−o)⋅σ(S)(1−σ(S))⋅x2e
Δ w 2 = − 0.1404 + ( 1 − 0.525 ) ∗ 0.525 ∗ ( 1 − 0.525 ) ∗ 2 = 0.0966 \Delta w_2 = - 0.1404 + ( 1 - 0.525 ) * 0.525 * ( 1 - 0.525 ) * 2 = 0.0966 Δw2=−0.1404+(1−0.525)∗0.525∗(1−0.525)∗2=0.0966

由于现在没有更多的例子了，因此我们使用所有样本累积的误差更新权重：
w 1 = 0.5 + ( − 0.1623 ) = 0.3966 w_1= 0.5 + ( -0.1623 ) = 0.3966 w1=0.5+(−0.1623)=0.3966
w 2 = 0.3 + 0.0966 = 0.3966 w_2= 0.3 + 0.0966 = 0.3966 w2=0.3+0.0966=0.3966
w 0 = − 1 + ( − 0.0219 ) = − 1.0219 w_0= - 1 + ( -0.0219 ) = -1.0219 w0=−1+(−0.0219)=−1.0219

4. 使用 Sigmoid 激活函数的感知机的增量梯度下降学习算法

类似地，我们有增量梯度下降学习算法。

步骤如下：

1. 初始化（Initialization）：
   样本集： { ( x e , y e ) } e = 1 N \{(x_e, y_e)\}_{e=1}^{N} {(xe,ye)}e=1N其中 x e x_e xe是输入特征， y e y_e ye是对应的输出标签。
   初始权重： w i w_i wi设置为小的随机值。
   学习率参数： η η η。
2. 重复执行（Repeat）：
   对于每个训练样本 ( x e , y e ) (x_e, y_e) (xe,ye)：
   计算模型的预测输出 o o o: o = σ ( S ) o = \sigma(S) o=σ(S)其中 S S S是加权输入和 S = ∑ i = 0 d w i x i e S = \sum_{i=0}^{d} w_i x_{ie} S=∑i=0dwixie
   如果感知机没有正确响应（即预测输出 o e o_e oe与实际输出 y e y_e ye不符），则根据以下规则更新权重： w i = w i + η ( y e − o e ) σ ( S ) ( 1 − σ ( S ) ) x i e w_i =w_i + \eta (y_e - o_e) \sigma(S)(1- \sigma(S))x_{ie} wi=wi+η(ye−oe)σ(S)(1−σ(S))xie
   重复上述过程，直到满足某个终止条件（如达到最大迭代次数、误差低于某个阈值或权重更新量非常小）。

5. 感知机（Perceptron）和梯度下降（Gradient Descent）的对比

这两种算法在寻找决策边界时有所不同：

1. 目标函数的不同：
   梯度下降：旨在最小化目标值（ y y y）与网络输出（ o o o）之间差的平方和，即最小化损失函数 ∑ ( y − o ) 2 ∑(y−o)^2 ∑(y−o)2。这种方法关注的是输出值与目标值之间的差异，而不仅仅是分类正确与否。
   感知机：旨在最小化分类错误，即最小化 ∑ 1 ( y ≠ s i g n ( w ⋅ x ) ) ∑1(y\neq sign(w⋅x)) ∑1(y=sign(w⋅x))，其中 1 1 1是指示函数，当条件满足时取值为1，否则为0。这种方法直接关注分类是否正确。
2. 决策边界：
   梯度下降：找到的决策边界可能会使得更多的实例被错误分类，与感知机规则相比，可能会有更高的错误分类率。这是因为梯度下降不仅关注分类的正确性，还关注输出值与目标值之间的差异大小。
   感知机：如果问题是线性可分的，感知机规则能找到一个决策边界，使得分类错误最小化。感知机规则保证能找到一个分离超平面，将不同类别的数据点分开。
3. 收敛性：
   感知机规则：对于线性可分问题，感知机规则保证收敛到一个分离超平面。这意味着，如果数据集是线性可分的，感知机最终能找到一个能够正确分类所有数据点的模型。
   梯度下降：虽然也能找到一个决策边界，但不保证这个边界能最小化分类错误，特别是在非凸损失函数的情况下。

5.1 误差曲面

误差曲面是一个多维空间中的曲面，其中每个维度对应一个模型参数（例如权重），而曲面的高度表示模型的误差（或损失函数的值）。

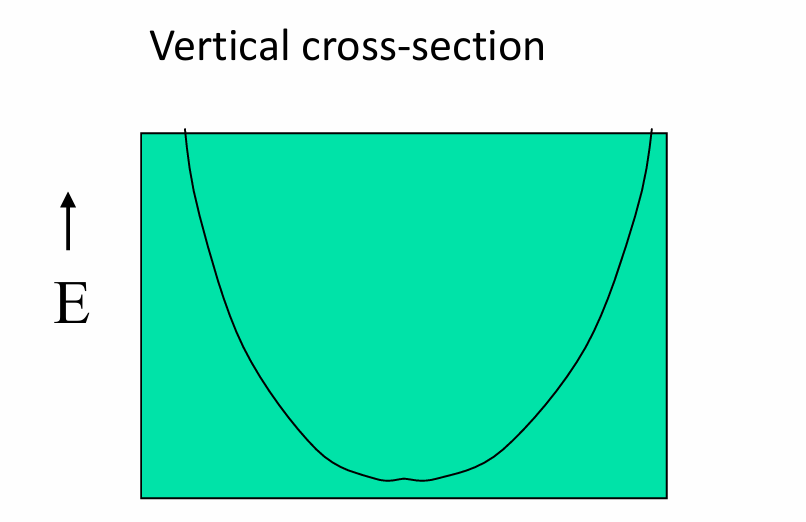
对于一个线性神经元（感知机），误差曲面是一个二次曲面（quadratic bowl），这意味着它在形状上类似于一个碗。

垂直于误差轴的截面（vertical cross-sections）是抛物线（parabolas），这表明在单个权重维度上，误差随着权重的变化而变化，呈现出一个U形。

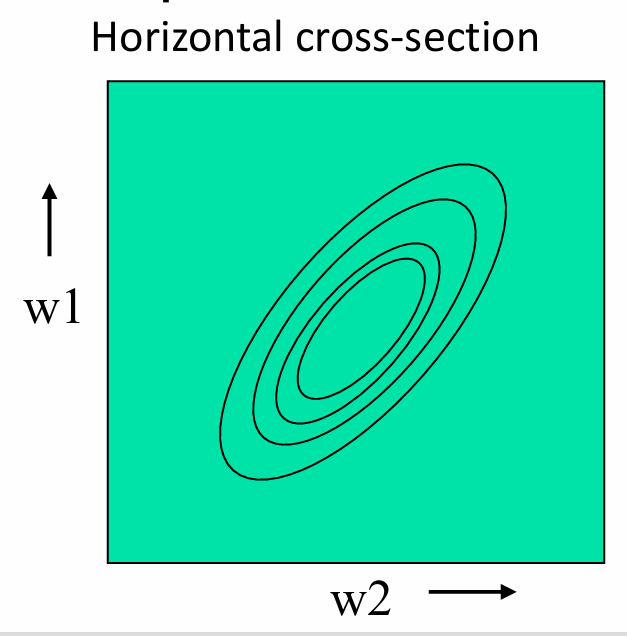
水平截面（horizontal cross-sections）是椭圆（ellipses），这表明在两个权重维度上，误差曲面的形状是椭圆形的。

5.2 批量学习（Batch learning）和增量学习（Incremental learning）的对比

批量学习在每次更新权重之前，会计算整个训练集上的误差。这意味着算法会使用所有样本的信息来确定梯度方向，然后沿着这个方向更新权重。

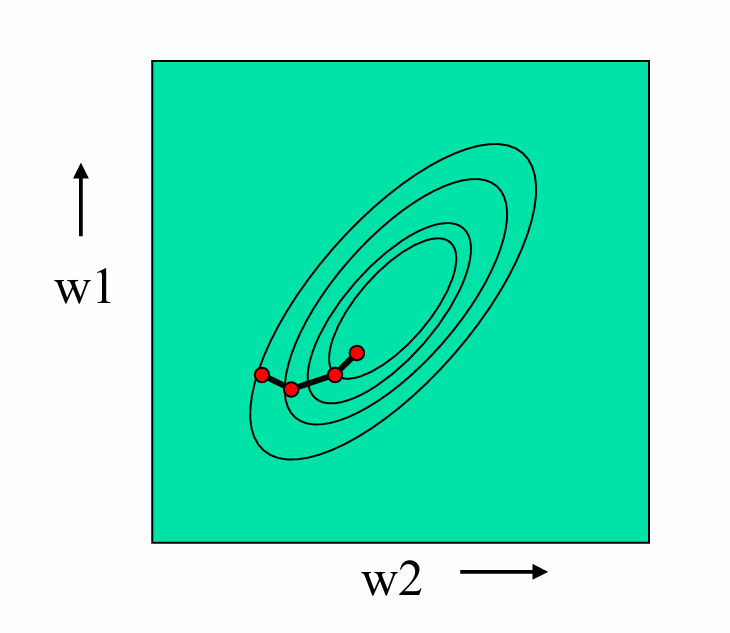
这种方法的优点是可以确保每次更新都是朝着全局最小值的方向进行的，从而可能更快地收敛到最优解。

增量学习在处理每个训练样本后立即更新权重。这意味着算法只使用当前样本的信息来计算梯度，并立即更新权重。

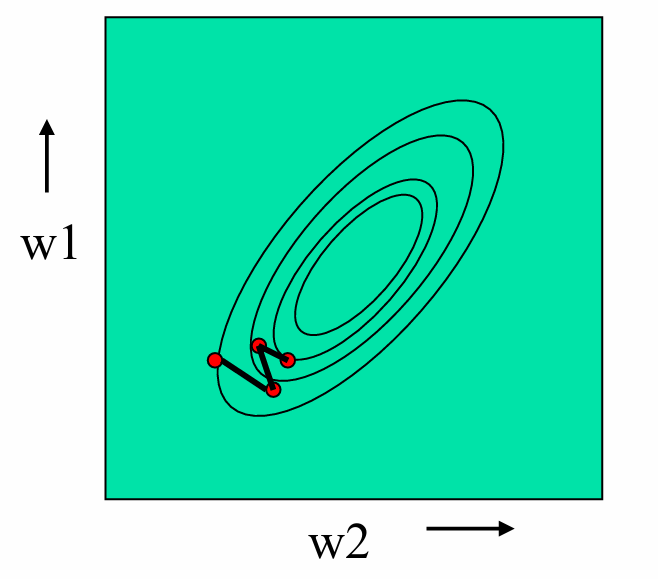
这种方法可能会在误差曲面上"跳跃"，因为它每次只考虑一个样本的信息，而不是整个训练集。