算法中的链表结构

准备工作：静态实现链表的原因

在算法竞赛中，静态实现链表（用数组模拟）比使用动态链表（如C++的std::list或手动new/delete创建节点）更常见，核心原因是效率、稳定性和可控性的综合考量，具体如下：

1. 避免动态内存分配的开销

动态链表的节点需要通过new（C++）或malloc（C）动态分配内存，删除时需要delete或free。这类操作的问题在于：

• 时间开销大：动态内存分配涉及操作系统的内存管理（如查找空闲块、修改内存链表等），单次操作的时间复杂度看似是O(1)，但实际常数极大（可能比数组下标访问慢几个数量级）。在竞赛中，当数据量达到1e5甚至1e6级别时，频繁的动态分配会直接导致超时。
• 内存碎片：频繁的分配和释放会导致内存碎片，进一步降低内存管理效率，极端情况下可能触发意外的内存分配失败。

而静态链表通过预先定义大数组 （如const int N = 1e5 + 10）存储节点，访问和修改仅通过数组下标（本质是指针的简化，直接访问内存地址），时间开销接近O(1)且常数极小，完全规避了动态分配的问题。

2. 更强的可控性和稳定性

• 避免空指针错误 ：动态链表依赖指针（如Node*），若操作不当（如访问已删除的节点、未初始化的指针）会导致空指针异常（NULL访问），在竞赛中这类错误难以调试且可能直接导致程序崩溃。

  静态链表用数组下标（如0作为哨兵/空节点标志），通过预先初始化数组（如下标0固定为"空"），可天然避免空指针问题，逻辑更稳定。

• 内存上限可控 ：竞赛题目通常会明确数据范围（如"节点数不超过1e5"），静态链表可通过定义N为略大于数据范围的值（如1e5 + 10），确保内存足够且不浪费。而动态链表若分配过量可能导致内存超限（MLE），分配不足则会运行时错误，可控性差。

3. 适配竞赛的特殊操作需求

算法竞赛中，链表常被用于实现更复杂的数据结构（如邻接表、单调队列、并查集的扩展等），或需要快速访问前驱/后继、批量操作节点的场景。静态链表的数组下标特性使其：

• 支持O(1)时间的随机访问（通过下标直接定位节点），而动态链表需要从头遍历，效率极低。
• 便于调试和输出中间状态（直接打印数组下标即可追踪节点关系），动态链表的指针地址无实际意义，难以调试。

4. 代码简洁，减少冗余

静态链表的实现仅需几个数组（如e[]存储值、pre[]/ne[]存储前驱/后继下标）和简单的索引管理（id记录当前可用节点），代码量极少，且逻辑清晰。例如：

int e[N], ne[N], id;  // 单链表核心定义
void init() { id = 0; }
void insert(int p, int x) { e[++id] = x; ne[id] = ne[p]; ne[p] = id; }

而动态链表需要定义节点结构体、处理指针操作，代码冗长且易出错，在时间紧张的竞赛中会浪费宝贵时间。

总结

算法竞赛的核心目标是在限制时间和内存内通过所有测试用例，静态链表通过"空间换时间"和"预先分配内存"，完美适配了竞赛对效率、稳定性和简洁性的需求。动态链表的灵活性在竞赛场景中优势有限，反而因开销和风险成为劣势，因此静态实现成为主流选择。

一.单链表

1.概念

静态链表的实现原理：

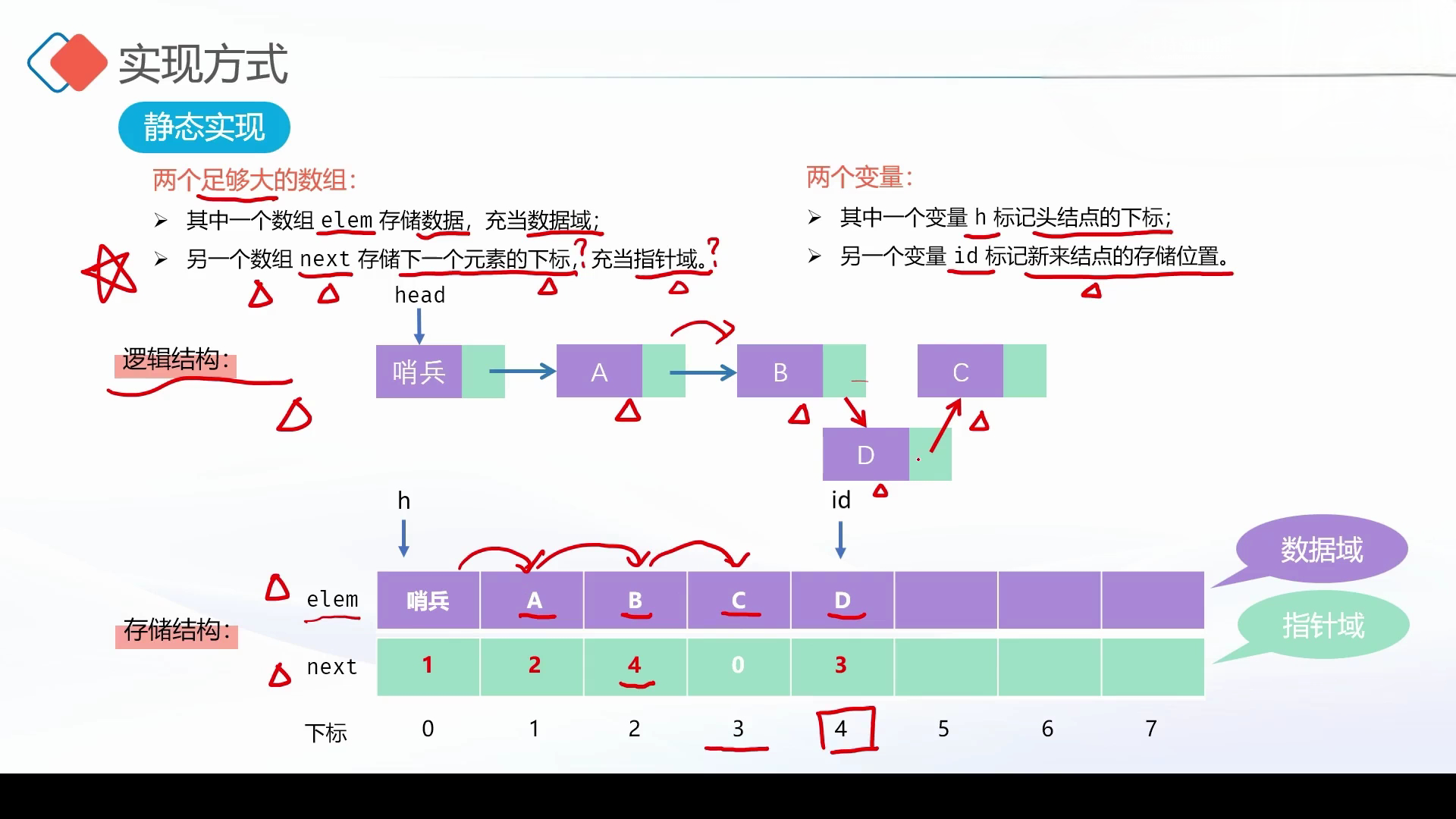
• 实现方式：静态实现，用数组模拟链表，避免动态分配内存的复杂操作
• 核心组成 ：
  • 两个数组：elem（数据域，存节点数据）、next（指针域，存下一个节点下标 ）
  • 两个变量：h（标记头结点下标，图中"哨兵"对应头结点，简化操作 ）、id（标记新节点存储位置，记录可用空间 ）
• 逻辑与存储 ：通过next数组构建逻辑链表结构（逻辑上是链式关系），实际存储在数组里（物理上是连续/离散数组空间 ），用下标模拟指针关联节点，实现链表的插入、删除等操作 ，比如插入新节点时，更新next数组下标，就能改变节点的逻辑连接 。

2.示例代码

#include<iostream>
using namespace std;

// 定义数组大小常量，1e3表示1000，用于存储链表节点
const int N = 1e3;

// e[]: 存储节点的值，e是elem
// ne[]: 存储节点的next指针，即下一个节点的索引,ne是next
// h: 头节点的索引（哨兵节点）
// id: 用于分配新节点的索引，记录当前已使用的节点数量
int e[N], ne[N], h, id;
// mp[]: 映射表，用于快速查找值对应的节点索引（哈希表思想）
int mp[N];

// 在链表头部插入一个新节点，值为x
void push_front(int x)
{
    id++;  // 分配新的节点索引（从1开始）
    e[id] = x;  // 存储节点的值
    mp[x] = id;  // 记录值x对应的节点索引，用于快速查找

    // 将新节点插入到哨兵节点和原头节点之间
    ne[id] = ne[h];  // 新节点的next指向原头节点
    ne[h] = id;      // 哨兵节点的next指向新节点，使新节点成为新的头节点
}

// 在链表中指定位置插入新节点
// 参数p：插入位置的前驱节点编号
// 参数x：要插入的节点值
void insert(int p, int x) {
    // 生成新节点的唯一编号（假设id是全局变量，用于记录节点总数）
    id++;
    // 存储新节点的值
    e[id] = x;
    // 建立值到节点编号的映射（便于快速查找节点）
    mp[x] = id;

    // 将新节点的后继指针指向p节点原来的后继节点
    ne[id] = ne[p];
    // 将p节点的后继指针指向新节点，完成插入操作
    ne[p] = id;
}


// 删除链表中指定节点的后继节点
// 参数p：要删除节点的前驱节点编号
void erase(int p)
{
    // 检查p节点是否有后继节点
    if (ne[p])
    {
        // 清除被删除节点的值到编号的映射
        mp[e[ne[p]]] = 0;
        // 将p节点的后继指针指向被删除节点的后继节点，完成删除操作
        ne[p] = ne[ne[p]];
    }
}

// 查找值为x的节点的索引
int find(int x)
{
    /* 注释掉的是遍历查找方式，时间复杂度O(n)
    for (int i = ne[h]; i; i = ne[i])
    {
        if (i == x) return i;
    }
    return -1;
    */

    // 使用映射表查找，时间复杂度O(1)
    return mp[x];
}

// 打印链表中的所有节点索引
void print()
{
    // 从哨兵节点的下一个节点开始遍历，直到遇到0（链表结束标志）
    for (int i = ne[h]; i; i = ne[i])
        cout << i << " ";  // 输出当前节点的索引

    cout << endl;  // 换行
}

```cpp
int main() {
    // 初始化链表（哨兵节点h=0，无数据节点）
    h = 0;
    id = 0;
    cout << "初始化空链表，节点索引：";
    print();  // 空输出

    // 头插测试：插入10、20、30
    push_front(10);
    push_front(20);
    push_front(30);
    cout << "\n头插10、20、30后，节点索引：";
    print();  // 应输出3 2 1
    cout << "值30的索引：" << find(30) << "（预期3）\n";
    cout << "值20的索引：" << find(20) << "（预期2）\n";
    cout << "值10的索引：" << find(10) << "（预期1）\n";

    // 插入测试：在值20（索引2）后插入25
    insert(find(20), 25);
    cout << "\n在20后插入25，节点索引：";
    print();  // 应输出3 2 4 1
    cout << "值25的索引：" << find(25) << "（预期4）\n";

    // 删除测试：删除值25（索引4的前驱是2）
    erase(find(20));
    cout << "\n删除25后，节点索引：";
    print();  // 应输出3 2 1
    cout << "值25的索引（应清零）：" << find(25) << "（预期0）\n";

    // 查找不存在值测试
    cout << "\n查找值50的索引：" << find(50) << "（预期0）\n";

    // 删除头节点测试（删除30，前驱是哨兵h=0）
    erase(h);
    cout << "\n删除头节点30后，节点索引：";
    print();  // 应输出2 1
    cout << "值30的索引（应清零）：" << find(30) << "（预期0）\n";

    return 0;
}

二.双向链表

1.概念

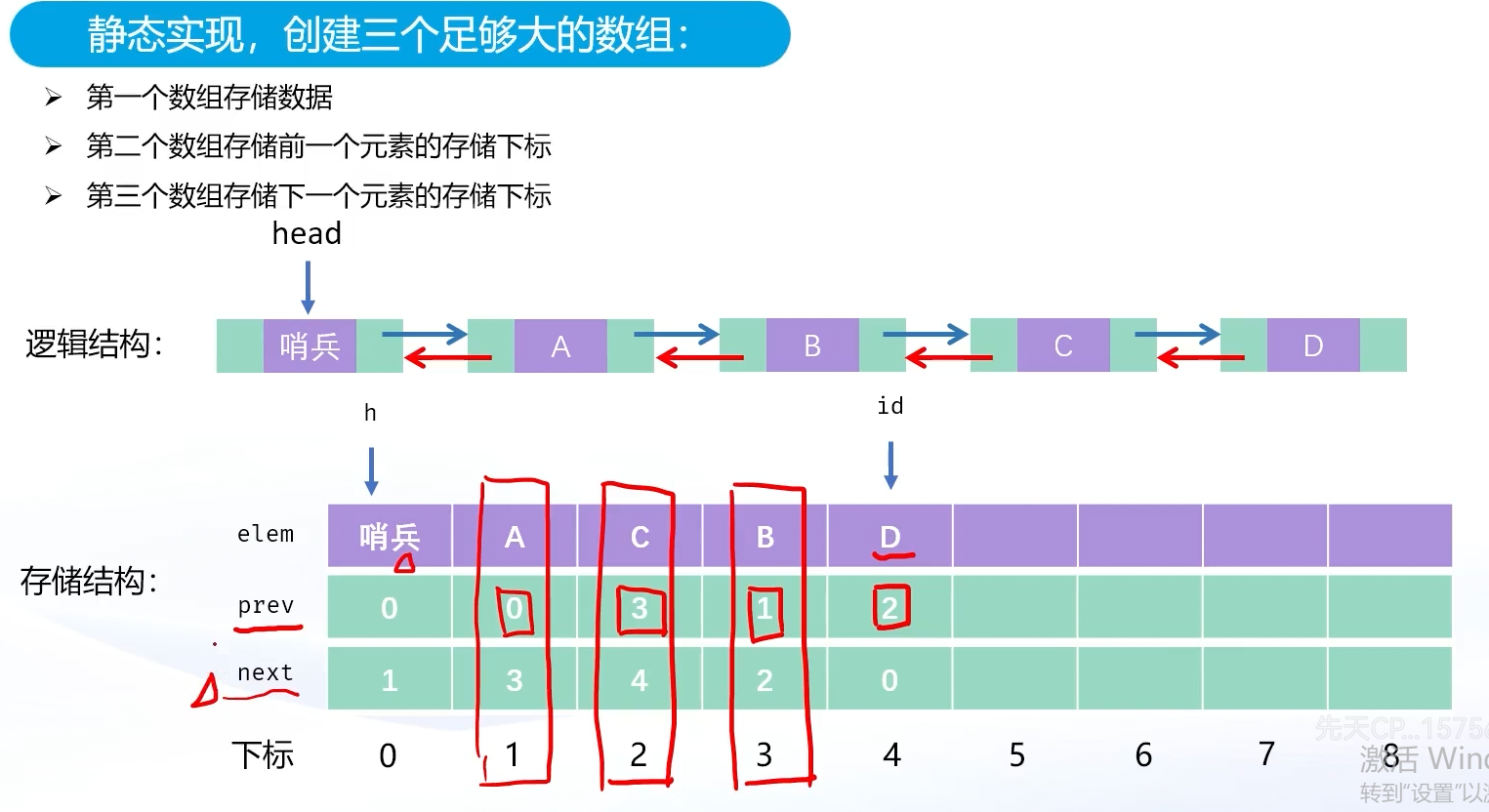
以上图片展示的是静态双向链表的实现原理，属于数据结构中链表的一种底层实现方式。

• 核心原理 ：
  • 通过三个数组模拟双向链表的节点结构：elem数组存储节点数据，prev数组存储前驱节点的下标，next数组存储后继节点的下标。
  • 引入"哨兵节点"（下标为0），用于简化链表的空表、头插、尾插等操作的边界条件处理。
• 逻辑与存储的对应 ：
  • 逻辑上的节点（如A、B、C、D）在存储结构中通过prev和next数组的下标关联，形成双向的遍历链路。例如节点A的prev为0（哨兵节点），next为3（节点C的下标），从而实现逻辑上的顺序关联。
• 用途 ：
  这种静态实现方式常用于编程竞赛或对内存管理要求特殊的场景，无需动态分配内存，通过数组下标即可快速维护节点的前驱和后继关系，同时利用哨兵节点避免了许多边界条件的判断，提升代码的简洁性和鲁棒性。

2.示例代码

#pragma once
#include <iostream>
using namespace std;

const int N = 1e5 + 10;  // 竞赛中通常预先定义足够大的数组大小

template <class T>
struct DoublyLinkedList {
    T e[N];         // 存储节点值
    int pre[N], ne[N];  // 前驱、后继数组
    int idx, head;   // idx: 当前可用节点索引，head: 哨兵节点（固定为0）

    // 初始化（替代构造函数，竞赛中常用init函数）
    void init() {
        head = 0;
        ne[head] = pre[head] = head;  // 哨兵节点自循环
        idx = 0;  // 从1开始分配节点（0作为哨兵）
    }

    // 头插
    void push_front(const T& x) {
        e[++idx] = x;
        pre[idx] = head;
        ne[idx] = ne[head];
        pre[ne[idx]] = idx;
        ne[head] = idx;
    }

    // 在pos前插入
    void insert(int pos, const T& x) {
        e[++idx] = x;
        pre[idx] = pre[pos];
        ne[idx] = pos;
        ne[pre[pos]] = idx;
        pre[pos] = idx;
    }

    // 在pos后插入（复用insert，等价于insert(ne[pos], x)）
    void insert_after(int pos, const T& x) {
        insert(ne[pos], x);
    }

    // 删除pos节点
    void erase(int pos) {
        ne[pre[pos]] = ne[pos];
        pre[ne[pos]] = pre[pos];
    }

    // 查找值为x的节点索引
    int find(const T& x) {
        for (int i = ne[head]; i != head; i = ne[i]) {
            if (e[i] == x) return i;
        }
        return -1;
    }

    // 打印链表
    void print() {
        for (int i = ne[head]; i != head; i = ne[i]) {
            cout << e[i] << " ";
        }
        cout << endl;
    }
};

// 测试函数
int main() {
    // 测试整数类型双向链表
    DoublyLinkedList<int> list;
    list.init();
    cout << "=== 初始化空链表 ===" << endl;
    cout << "初始链表（空）：";
    list.print();  // 应输出空行

    // 测试头插
    list.push_front(3);
    list.push_front(2);
    list.push_front(1);
    cout << "\n=== 头插 1, 2, 3 后 ===" << endl;
    cout << "链表内容：";
    list.print();  // 应输出：1 2 3

    // 测试查找
    int pos = list.find(2);
    cout << "\n查找值为2的节点索引：" << pos << endl;  // 应输出2（插入顺序为1→2→3，索引依次为1,2,3）
    int invalid_pos = list.find(100);
    cout << "查找值为100的节点索引：" << invalid_pos << endl;  // 应输出-1

    // 测试在pos前插入（在2前面插入5）
    list.insert(pos, 5);
    cout << "\n=== 在2前面插入5后 ===" << endl;
    cout << "链表内容：";
    list.print();  // 应输出：1 5 2 3

    // 测试在pos后插入（在2后面插入6）
    list.insert_after(pos, 6);
    cout << "\n=== 在2后面插入6后 ===" << endl;
    cout << "链表内容：";
    list.print();  // 应输出：1 5 2 6 3

    // 测试删除节点（删除值为5的节点）
    int del_pos = list.find(5);
    list.erase(del_pos);
    cout << "\n=== 删除5后 ===" << endl;
    cout << "链表内容：";
    list.print();  // 应输出：1 2 6 3

    // 测试删除头节点（1）
    int head_node_pos = list.find(1);
    list.erase(head_node_pos);
    cout << "\n=== 删除1后 ===" << endl;
    cout << "链表内容：";
    list.print();  // 应输出：2 6 3

    // 测试删除尾节点（3）
    int tail_node_pos = list.find(3);
    list.erase(tail_node_pos);
    cout << "\n=== 删除3后 ===" << endl;
    cout << "链表内容：";
    list.print();  // 应输出：2 6

    return 0;
}