频率分集阵列雷达
P. Antonik, M. C. Wicks, H. D. Griffiths and C. J. Baker, "Frequency diverse array radars," 2006 IEEE Conference on Radar, Verona, NY, USA, 2006, pp. 3 pp.-
一、传统相控阵雷达的基本原理
在理解频率分集阵列之前,我们需要首先回顾传统相控阵的工作原理。传统相控阵由多个理想各向同性辐射器组成,所有辐射单元发射完全相同的电磁波形。当所有辐射信号都是具有相同相位的连续波信号时,根据惠更斯原理,各单元辐射的球面波在远场叠加形成平面波,天线波束将指向法线方向(broadside),即垂直于阵列孔径表面。对于远场中与法线方向成角度 θ \theta θ的目标,由于几何路径差异,不同阵元到达目标的电磁波将存在相位差。具体而言,相邻单元之间由于路径长度差引起的相位差可表示为:
ψ = 2 π d λ sin ( θ ) (1) \psi = \frac{2\pi d}{\lambda} \sin(\theta) \tag{1} ψ=λ2πdsin(θ)(1)
其中, d d d表示相邻阵元之间的物理间距, θ \theta θ是目标相对于阵列法线的角度, λ \lambda λ是发射信号的波长。这个相位差是相控阵能够进行波束扫描的物理基础。通过在各阵元上施加线性递增的相位,可以补偿或增强这种路径差引起的相位差,从而实现波束的电子扫描。
二、频率分集阵列
2.1 基本原理
频率分集阵列的核心创新在于打破了传统相控阵中所有阵元发射相同频率信号的限制。在这种新型阵列中,每个辐射单元的发射频率相对于相邻单元递增一个小的频率偏移量 Δ f \Delta f Δf。这种看似简单的改变带来了深远的影响:波束的指向不再仅仅依赖于角度,而是同时依赖于距离。
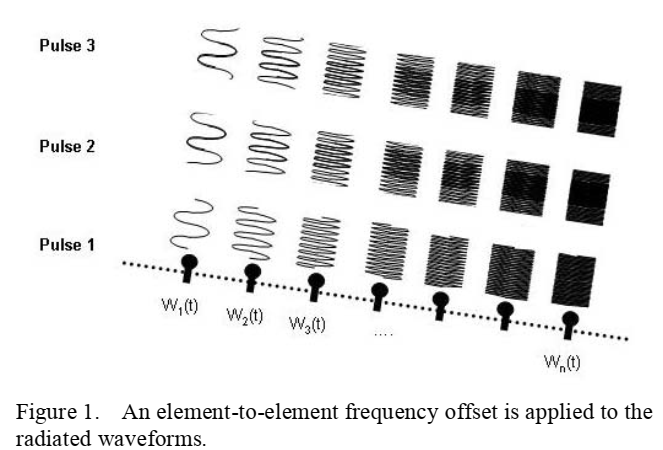
图1描述 :图1展示了频率分集阵列的基本工作原理。图中显示了一个线性阵列,包含多个辐射单元(标记为Pulse 1, Pulse 2, Pulse 3)。每个单元发射不同频率的信号,从左到右依次为 W 1 ( t ) W_1(t) W1(t)、 W 2 ( t ) W_2(t) W2(t)直到 W N ( t ) W_N(t) WN(t)。频率从第一个单元的基频开始,每个单元递增 Δ f \Delta f Δf,形成一个频率阶梯。这种频率分布导致了独特的空间-时间-频率耦合效应。
2.2 相位差分析
当考虑频率分集时,相邻单元之间的相位差不再是简单的几何路径差,而是包含了频率差异带来的额外项。根据电磁波传播理论,频率为 f 1 + i Δ f f_1 + i\Delta f f1+iΔf的第 i i i个阵元到达距离为 R R R、角度为 θ \theta θ的目标点的相位为:
ϕ i = 2 π ( f 1 + i Δ f ) ( t − R i c ) (2) \phi_i = 2\pi(f_1 + i\Delta f)\left(\frac{t - R_i}{c}\right) \tag{2} ϕi=2π(f1+iΔf)(ct−Ri)(2)
其中 R i R_i Ri是第 i i i个阵元到目标的距离。经过推导(详见附录A),相邻单元之间的相位差可以表示为:
Δ ψ = 2 π f 1 d sin ( θ ) c − 2 π R 1 Δ f c + 2 π Δ f d sin ( θ ) c (3) \Delta\psi = \frac{2\pi f_1 d \sin(\theta)}{c} - \frac{2\pi R_1 \Delta f}{c} + \frac{2\pi \Delta f d \sin(\theta)}{c} \tag{3} Δψ=c2πf1dsin(θ)−c2πR1Δf+c2πΔfdsin(θ)(3)
这个表达式揭示了频率分集阵列的独特特性。第一项 2 π f 1 d sin ( θ ) c \frac{2\pi f_1 d \sin(\theta)}{c} c2πf1dsin(θ)是传统的角度相关相位差;第二项 − 2 π R 1 Δ f c -\frac{2\pi R_1 \Delta f}{c} −c2πR1Δf是纯距离相关项,这是频率分集带来的新特性;第三项 2 π Δ f d sin ( θ ) c \frac{2\pi \Delta f d \sin(\theta)}{c} c2πΔfdsin(θ)是角度和频率偏移的耦合项。
2.3 波束指向特性
相位分布决定了阵列的波束指向,当相位差为零时,所有阵元的辐射在该方向上同相叠加,形成主瓣。因此,波束聚焦的表观角度 θ ′ \theta' θ′可通过令总相位差为零求得:
θ ′ = arcsin [ ( 1 − Δ f f 1 ) sin ( θ ) + R 1 Δ f f 1 d ] (4) \theta' = \arcsin\left[\left(1 - \frac{\Delta f}{f_1}\right) \sin(\theta) + \frac{R_1 \Delta f}{f_1 d}\right] \tag{4} θ′=arcsin[(1−f1Δf)sin(θ)+f1dR1Δf](4)
为了更清楚地理解这种距离相关特性,考虑一个简化情况:设定标称扫描角 θ = 0 \theta = 0 θ=0(即不施加额外的相位梯度),并设阵元间距 d = λ / 2 d = \lambda/2 d=λ/2。此时表观扫描角简化为:
θ ′ = arcsin [ 2 R 1 Δ f c ] (5) \theta' = \arcsin\left[\frac{2 R_1 \Delta f}{c}\right] \tag{5} θ′=arcsin[c2R1Δf](5)
这个简洁的表达式清楚地表明,波束指向角度 θ ′ \theta' θ′直接与目标距离 R 1 R_1 R1成正比。
三、距离相关波束特性的实验验证
3.1 数值仿真结果
为了直观展示频率分集阵列的独特特性,研究者进行了详细的数值仿真。考虑一个工作在X波段(约10 GHz)的16元线性阵列,阵元间距为半波长,频率增量 Δ f = 350 \Delta f = 350 Δf=350 Hz。
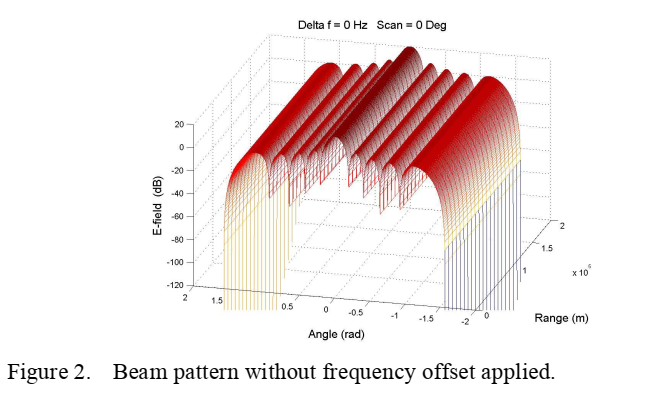
图2描述:图2展示了传统相控阵(无频率偏移)的二维波束方向图。横轴表示方位角(从-90°到+90°),纵轴表示距离(从0到10 km)。图中的波束图案呈现垂直条纹状,表明波束强度仅与角度有关而与距离无关。主瓣位于0°方向,在所有距离上保持恒定。颜色编码表示归一化的波束强度,深红色区域表示主瓣(0 dB),蓝色区域表示旁瓣(低于-30 dB)。
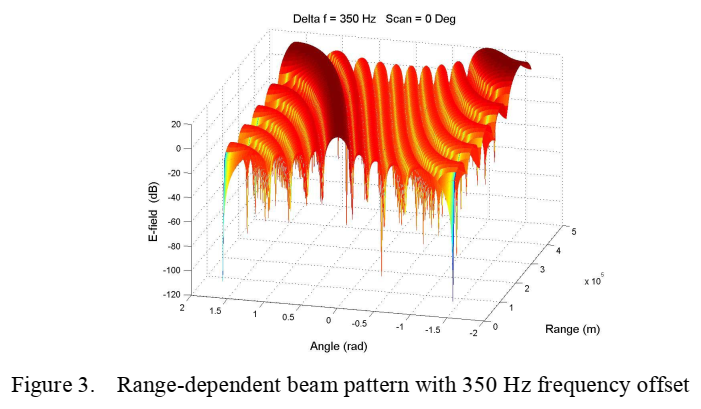
图3描述:图3展示了施加350 Hz频率偏移后的距离相关波束方向图。与图2相比,这幅图呈现出完全不同的特征。波束图案不再是垂直条纹,而是呈现出独特的"S"形曲线。在近距离(R = 0),波束指向0°;随着距离增加,波束逐渐偏转;在200 km处,波束已偏转至约27.8°。这种距离相关的波束扫描是频率分集阵列的标志性特征。图中还可以观察到,不同距离上的波束宽度基本保持不变,这表明频率分集主要影响波束指向而不是波束形状。
3.2 实际应用示例
以 Δ f = 350 \Delta f = 350 Δf=350 Hz为例进行定量分析。在天线面附近( R 1 = 0 R_1 = 0 R1=0),根据公式(5), θ ′ = arcsin ( 0 ) = 0 ° \theta' = \arcsin(0) = 0° θ′=arcsin(0)=0°,波束指向法线方向。随着距离增加,波束指向角度线性增长:
- 在 R 1 = 50 R_1 = 50 R1=50 km处: θ ′ ≈ 6.9 ° \theta' \approx 6.9° θ′≈6.9°
- 在 R 1 = 100 R_1 = 100 R1=100 km处: θ ′ ≈ 13.9 ° \theta' \approx 13.9° θ′≈13.9°
- 在 R 1 = 200 R_1 = 200 R1=200 km处: θ ′ ≈ 27.8 ° \theta' \approx 27.8° θ′≈27.8°
这种特性为雷达系统提供了独特的能力,可以在不改变硬件配置的情况下,通过调整频率增量 Δ f \Delta f Δf来控制波束的距离扫描率。
四、广义频率分集阵列架构
4.1 波形设计的一般化
前面的分析假设所有辐射信号都是连续波,仅在频率上有差异。然而,实际雷达系统需要更复杂的波形设计。在广义频率分集阵列中,从第 i i i个天线在第 j j j个脉冲上辐射的波形可以表示为:
W i , j ( t ) = ϕ i , j ( t ) ⊗ W i , j 0 ( t ) (6) W_{i,j}(t) = \phi_{i,j}(t) \otimes W^0_{i,j}(t) \tag{6} Wi,j(t)=ϕi,j(t)⊗Wi,j0(t)(6)
其中 W i , j 0 ( t ) W^0_{i,j}(t) Wi,j0(t)包含频率分集但无相位分集的基本波形, ϕ i , j ( t ) \phi_{i,j}(t) ϕi,j(t)包含所有相位调制信息。这种分离允许独立控制频率和相位特性。
相位编码 ϕ i , j \phi_{i,j} ϕi,j可以采用多种方案,每种方案都有其特定的优势:
- 随机PSK:提供良好的自相关和互相关特性,适用于抗干扰应用
- M进制PSK:允许在相位域传输额外信息
- Costas编码:优化模糊函数特性,改善距离-多普勒分辨率
- OFDM:支持高数据率通信功能的集成
- 遗传算法优化:根据特定性能指标自适应优化波形
4.2 系统架构模型
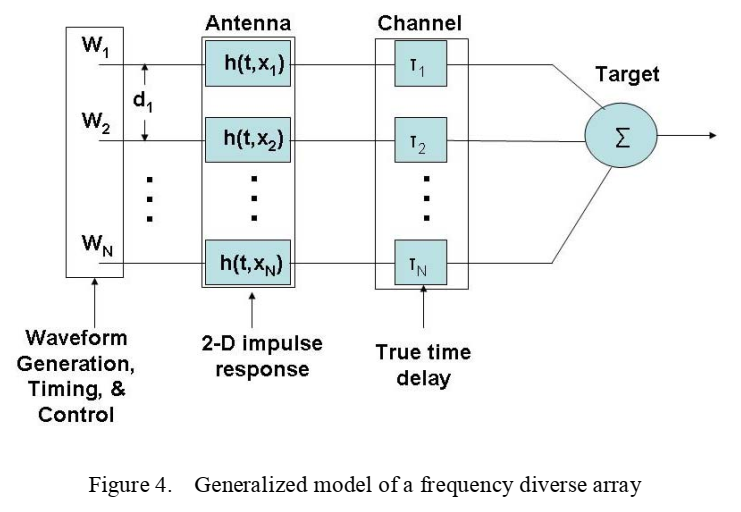
图4描述 :图4展示了广义频率分集阵列的完整系统模型。该模型包含多个层次的信号处理和控制。最左侧是波形生成、定时和控制模块,负责产生基带波形 W 1 W_1 W1到 W N W_N WN。每个波形经过独立的天线通道,包含二维脉冲响应函数 h ( t , x i ) h(t,x_i) h(t,xi),可以建模天线单元的时空特性包括互耦效应。通道输出经过真时延(TTD)单元 T i T_i Ti进行精确的相位控制。信号经过功率放大后,通过天线单元辐射到空间,最终在目标位置叠加。这个模型的关键创新在于允许每个维度(时间、空间、频率、相位、极化)的独立控制。
4.3 硬件实现方案
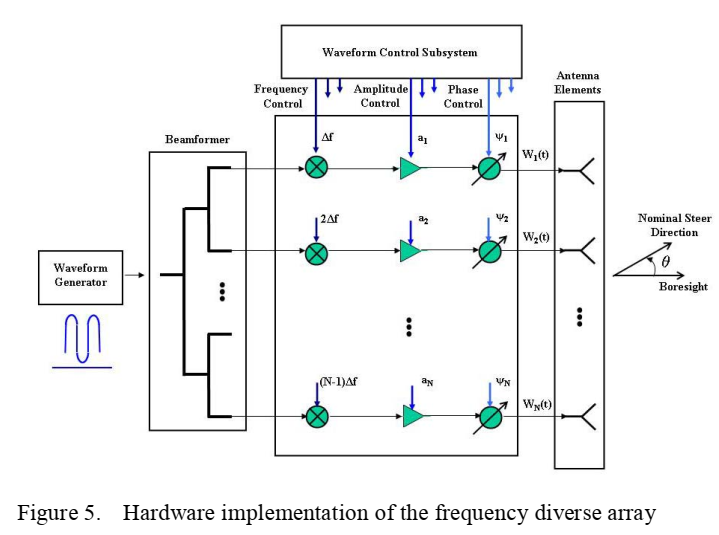
图5描述 :图5详细展示了频率分集阵列的硬件实现架构。系统核心是波形控制子系统,包含现场可编程门阵列(FPGA)实现的数字波形生成器。频率控制通过直接数字综合器(DDS)实现,可以精确控制每个通道的频率和相位。系统包含 N N N个独立的收发(T/R)模块,每个模块都有独立的上/下变频链路。相位控制既可以通过数字域实现,也可以通过模拟移相器实现。幅度控制通过可变增益放大器(VGA)实现。所有控制参数通过高速数字总线实时更新,支持脉冲间的动态重配置。
五、动态空间通道分配
5.1 时变孔径配置
频率分集阵列的一个重要扩展是支持动态的空间通道分配,这对于机载和分布式雷达系统尤其重要。
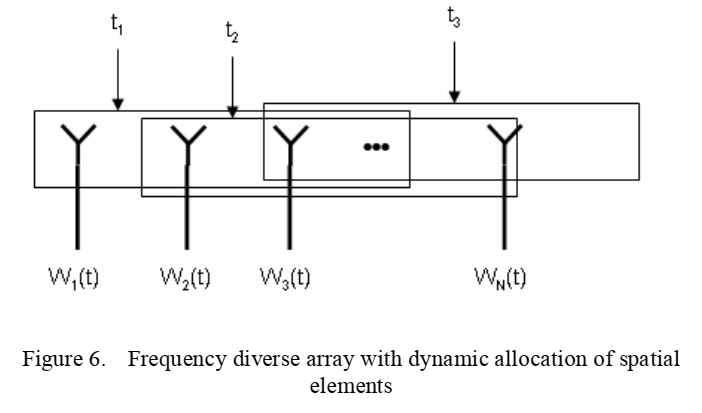
图6描述 :图6说明了移动平台上频率分集阵列的动态分配概念。图中显示了一个大型孔径,在不同时刻( t 1 t_1 t1, t 2 t_2 t2, t 3 t_3 t3)选择不同的子孔径进行工作。每个时刻,系统根据任务需求选择最优的阵元组合,并为每个活动阵元分配相应的波形参数 W i , j ( t ) W_{i,j}(t) Wi,j(t)。这种动态配置允许系统同时执行多种任务,例如在 t 1 t_1 t1时刻进行SAR成像,在 t 2 t_2 t2时刻进行GMTI,在 t 3 t_3 t3时刻进行通信。箭头表示随着平台移动,有效相位中心的变化轨迹。
5.2 多任务并行操作
通过在空间、快时间、慢时间和频率维度上的灵活控制,广义频率分集阵列可以实现前所未有的多任务并行能力。例如,可以将孔径分成多个子阵列,每个子阵列执行不同的任务:
- 子阵列1:执行高分辨率SAR成像,使用宽带线性调频信号
- 子阵列2:进行GMTI处理,使用优化的空时自适应处理(STAP)
- 子阵列3:维持数据链通信,使用OFDM波形
这种能力通过传统相控阵是难以实现的,因为传统系统中所有阵元必须工作在相同频率。
六、技术优势与应用前景
6.1 抗干扰能力
频率分集阵列的距离相关特性为抗干扰提供了新的维度。对于位于特定距离的干扰源,可以通过调整频率增量使该距离处的波束指向零点,从而实现空间滤波。这种能力对于对抗多径干扰特别有效,因为直达路径和反射路径通常具有不同的传播距离。
6.2 安全通信
距离-角度耦合特性可以用于实现物理层安全通信。只有位于特定距离和角度组合的接收机才能正确接收信号,其他位置的窃听者将接收到严重失真的信号。通过动态改变频率增量,可以实现通信链路的动态加密。
6.3 高分辨率成像
在SAR应用中,频率分集可以提供额外的信息维度。传统SAR依赖平台运动产生的多普勒频移来实现方位向分辨率,而频率分集阵列可以在不依赖平台运动的情况下产生类似的效果,这对于悬停平台或慢速平台特别有价值。
七、技术挑战与解决方案
尽管频率分集阵列具有诸多优势,但在实际应用中仍面临一些技术挑战:
7.1 频率同步
保持所有通道之间精确的频率关系是系统性能的关键。即使很小的频率误差也会导致波束形状畸变和增益损失。解决方案包括使用高稳定度的主振荡器和精确的频率综合技术。现代DDS技术可以提供优于 1 0 − 12 10^{-12} 10−12的频率精度,足以满足大多数应用需求。
7.2 互耦效应
当阵元工作在不同频率时,互耦效应变得更加复杂。传统的互耦补偿方法假设所有阵元工作在相同频率,不能直接应用。需要开发新的校准算法,考虑频率相关的互耦矩阵。一种方法是在系统设计阶段通过电磁仿真建立完整的互耦模型,然后在信号处理中进行预补偿。
7.3 宽带匹配
由于不同阵元工作在不同频率,天线和馈电网络需要在更宽的频带内保持良好匹配。这要求采用宽带天线设计和宽带匹配网络。超宽带天线技术的发展为这一问题提供了解决方案。
附录A:频率分集阵列相位差的推导
考虑一个 N N N元线性阵列,阵元间距为 d d d,第 i i i个阵元的位置为 x i = i d x_i = id xi=id(以第0个阵元为参考)。第 i i i个阵元发射频率为 f i = f 0 + i Δ f f_i = f_0 + i\Delta f fi=f0+iΔf的连续波信号。
对于位于极坐标 ( R , θ ) (R, \theta) (R,θ)的目标点,第 i i i个阵元到目标的距离为:
R i = R 2 + x i 2 − 2 R x i sin θ (A1) R_i = \sqrt{R^2 + x_i^2 - 2Rx_i\sin\theta} \tag{A1} Ri=R2+xi2−2Rxisinθ (A1)
在远场条件下( R ≫ x i R \gg x_i R≫xi),可以使用泰勒展开:
R i ≈ R − x i sin θ + x i 2 cos 2 θ 2 R − x i 3 sin θ cos 2 θ 2 R 2 + ⋯ (A2) R_i \approx R - x_i\sin\theta + \frac{x_i^2\cos^2\theta}{2R} - \frac{x_i^3\sin\theta\cos^2\theta}{2R^2} + \cdots \tag{A2} Ri≈R−xisinθ+2Rxi2cos2θ−2R2xi3sinθcos2θ+⋯(A2)
通常保留前两项即可:
R i ≈ R − x i sin θ = R − i d sin θ (A3) R_i \approx R - x_i\sin\theta = R - id\sin\theta \tag{A3} Ri≈R−xisinθ=R−idsinθ(A3)
第 i i i个阵元发射的信号到达目标点的相位为:
ϕ i = 2 π f i R i c = 2 π ( f 0 + i Δ f ) R − i d sin θ c (A4) \phi_i = 2\pi f_i \frac{R_i}{c} = 2\pi(f_0 + i\Delta f)\frac{R - id\sin\theta}{c} \tag{A4} ϕi=2πficRi=2π(f0+iΔf)cR−idsinθ(A4)
展开得:
ϕ i = 2 π f 0 R c − 2 π f 0 i d sin θ c + 2 π i Δ f R c − 2 π i 2 Δ f d sin θ c (A5) \phi_i = \frac{2\pi f_0 R}{c} - \frac{2\pi f_0 id\sin\theta}{c} + \frac{2\pi i\Delta f R}{c} - \frac{2\pi i^2\Delta f d\sin\theta}{c} \tag{A5} ϕi=c2πf0R−c2πf0idsinθ+c2πiΔfR−c2πi2Δfdsinθ(A5)
相邻阵元(第 i i i和第 i + 1 i+1 i+1个)之间的相位差为:
Δ ϕ = ϕ i + 1 − ϕ i (A6) \Delta\phi = \phi_{i+1} - \phi_i \tag{A6} Δϕ=ϕi+1−ϕi(A6)
代入并化简:
Δ ϕ = − 2 π f 0 d sin θ c + 2 π Δ f R c − 2 π ( 2 i + 1 ) Δ f d sin θ c (A7) \Delta\phi = -\frac{2\pi f_0 d\sin\theta}{c} + \frac{2\pi \Delta f R}{c} - \frac{2\pi(2i+1)\Delta f d\sin\theta}{c} \tag{A7} Δϕ=−c2πf0dsinθ+c2πΔfR−c2π(2i+1)Δfdsinθ(A7)
对于阵列中心附近的阵元( i ≈ N / 2 i \approx N/2 i≈N/2),当 N N N足够大时,最后一项中的 2 i + 1 ≈ N 2i+1 \approx N 2i+1≈N,可以写成平均形式:
Δ ϕ ≈ 2 π f 0 d sin θ c − 2 π R Δ f c + 2 π Δ f d sin θ c (A8) \Delta\phi \approx \frac{2\pi f_0 d\sin\theta}{c} - \frac{2\pi R\Delta f}{c} + \frac{2\pi \Delta f d\sin\theta}{c} \tag{A8} Δϕ≈c2πf0dsinθ−c2πRΔf+c2πΔfdsinθ(A8)
这就是正文中的公式(3),其中使用了 f 1 f_1 f1代替 f 0 f_0 f0表示第一个阵元的频率。
附录B:表观扫描角的推导
波束主瓣形成的条件是所有阵元的贡献同相叠加,即相位差为零或 2 π 2\pi 2π的整数倍。对于主瓣,我们有:
Δ ϕ = 0 (B1) \Delta\phi = 0 \tag{B1} Δϕ=0(B1)
将公式(A8)代入:
2 π f 0 d sin θ ′ c − 2 π R Δ f c + 2 π Δ f d sin θ ′ c = 0 (B2) \frac{2\pi f_0 d\sin\theta'}{c} - \frac{2\pi R\Delta f}{c} + \frac{2\pi \Delta f d\sin\theta'}{c} = 0 \tag{B2} c2πf0dsinθ′−c2πRΔf+c2πΔfdsinθ′=0(B2)
其中 θ ′ \theta' θ′表示波束指向的表观角度。化简得:
sin θ ′ = R Δ f d ( f 0 + Δ f ) (B3) \sin\theta' = \frac{R\Delta f}{d(f_0 + \Delta f)} \tag{B3} sinθ′=d(f0+Δf)RΔf(B3)
如果存在一个预设的扫描角 θ 0 \theta_0 θ0(通过相位加权实现),则:
sin θ ′ = sin θ 0 + R Δ f d ⋅ f 0 ⋅ 1 1 + Δ f / f 0 (B4) \sin\theta' = \sin\theta_0 + \frac{R\Delta f}{d \cdot f_0} \cdot \frac{1}{1 + \Delta f/f_0} \tag{B4} sinθ′=sinθ0+d⋅f0RΔf⋅1+Δf/f01(B4)
由于通常 Δ f ≪ f 0 \Delta f \ll f_0 Δf≪f0,可以近似为:
sin θ ′ ≈ sin θ 0 ( 1 − Δ f f 0 ) + R Δ f d ⋅ f 0 (B5) \sin\theta' \approx \sin\theta_0\left(1 - \frac{\Delta f}{f_0}\right) + \frac{R\Delta f}{d \cdot f_0} \tag{B5} sinθ′≈sinθ0(1−f0Δf)+d⋅f0RΔf(B5)
因此:
θ ′ = arcsin [ ( 1 − Δ f f 0 ) sin θ 0 + R Δ f d ⋅ f 0 ] (B6) \theta' = \arcsin\left[\left(1 - \frac{\Delta f}{f_0}\right)\sin\theta_0 + \frac{R\Delta f}{d \cdot f_0}\right] \tag{B6} θ′=arcsin[(1−f0Δf)sinθ0+d⋅f0RΔf](B6)
这就是正文中的公式(4)。
附录C:波束方向图的数学表达
频率分集阵列的归一化方向图可以表示为:
F ( R , θ ) = 1 N ∣ ∑ i = 0 N − 1 exp [ j ϕ i ( R , θ ) ] ∣ (C1) F(R, \theta) = \frac{1}{N}\left|\sum_{i=0}^{N-1} \exp\left[j\phi_i(R, \theta)\right]\right| \tag{C1} F(R,θ)=N1 i=0∑N−1exp[jϕi(R,θ)] (C1)
其中 ϕ i ( R , θ ) \phi_i(R, \theta) ϕi(R,θ)由公式(A5)给出。展开求和:
F ( R , θ ) = 1 N ∣ ∑ i = 0 N − 1 exp [ j 2 π c ( f 0 R − f 0 i d sin θ + i Δ f R − i 2 Δ f d sin θ ) ] ∣ (C2) F(R, \theta) = \frac{1}{N}\left|\sum_{i=0}^{N-1} \exp\left[j\frac{2\pi}{c}\left(f_0R - f_0id\sin\theta + i\Delta fR - i^2\Delta fd\sin\theta\right)\right]\right| \tag{C2} F(R,θ)=N1 i=0∑N−1exp[jc2π(f0R−f0idsinθ+iΔfR−i2Δfdsinθ)] (C2)
提取公共相位因子:
F ( R , θ ) = ∣ 1 N ∑ i = 0 N − 1 exp [ − j 2 π i c ( f 0 d sin θ − Δ f R + i Δ f d sin θ ) ] ∣ (C3) F(R, \theta) = \left|\frac{1}{N}\sum_{i=0}^{N-1} \exp\left[-j\frac{2\pi i}{c}\left(f_0d\sin\theta - \Delta fR + i\Delta fd\sin\theta\right)\right]\right| \tag{C3} F(R,θ)= N1i=0∑N−1exp[−jc2πi(f0dsinθ−ΔfR+iΔfdsinθ)] (C3)
令:
β = 2 π c ( f 0 d sin θ − Δ f R ) (C4) \beta = \frac{2\pi}{c}\left(f_0d\sin\theta - \Delta fR\right) \tag{C4} β=c2π(f0dsinθ−ΔfR)(C4)
γ = 2 π Δ f d sin θ c (C5) \gamma = \frac{2\pi\Delta fd\sin\theta}{c} \tag{C5} γ=c2πΔfdsinθ(C5)
则方向图可以写为:
F ( R , θ ) = ∣ 1 N ∑ i = 0 N − 1 exp [ − j ( i β + i 2 γ ) ] ∣ (C6) F(R, \theta) = \left|\frac{1}{N}\sum_{i=0}^{N-1} \exp\left[-j(i\beta + i^2\gamma)\right]\right| \tag{C6} F(R,θ)= N1i=0∑N−1exp[−j(iβ+i2γ)] (C6)
当 γ = 0 \gamma = 0 γ=0(即 Δ f = 0 \Delta f = 0 Δf=0)时,这退化为传统相控阵的方向图:
F ( θ ) = ∣ sin ( N β / 2 ) N sin ( β / 2 ) ∣ (C7) F(\theta) = \left|\frac{\sin(N\beta/2)}{N\sin(\beta/2)}\right| \tag{C7} F(θ)= Nsin(β/2)sin(Nβ/2) (C7)
当 γ ≠ 0 \gamma \neq 0 γ=0时,方向图呈现距离相关特性。这个和式没有简单的闭式解,但可以通过数值方法计算,结果如正文图2和图3所示。
附录D:频率分集阵列的模糊函数分析
雷达波形的分辨能力可以通过模糊函数来表征。对于频率分集阵列,模糊函数需要在传统的时延-多普勒维度基础上增加空间维度。广义模糊函数定义为:
χ ( τ , f d , θ ) = ∫ − ∞ ∞ s ∗ ( t ) s ( t + τ ) e j 2 π f d t w ( θ ) d t (D1) \chi(\tau, f_d, \theta) = \int_{-\infty}^{\infty} s^*(t) s(t+\tau) e^{j2\pi f_d t} w(\theta) dt \tag{D1} χ(τ,fd,θ)=∫−∞∞s∗(t)s(t+τ)ej2πfdtw(θ)dt(D1)
其中 s ( t ) s(t) s(t)是复合波形, w ( θ ) w(\theta) w(θ)是空间加权函数。对于频率分集阵列:
s ( t ) = ∑ i = 0 N − 1 s i ( t ) e j 2 π ( f 0 + i Δ f ) t (D2) s(t) = \sum_{i=0}^{N-1} s_i(t) e^{j2\pi(f_0 + i\Delta f)t} \tag{D2} s(t)=i=0∑N−1si(t)ej2π(f0+iΔf)t(D2)
代入并展开,可以得到频率分集阵列特有的距离-角度耦合特性在模糊函数中的体现。这种耦合可以用来改善某些维度的分辨率,但代价是在其他维度产生额外的模糊。