复习下线性代数，使用向量平移拼接两段线

数学原理

1. 线段长度的平方 = 线段两端端点组成向量与其自身的内积

2. 向量外点向向量上投影的相对位置 t

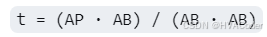
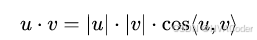
第一种情况，P向AB投影在AB中间，cosθ > 0

AP AB向量点积等于AB，AP的模以及cosθ乘积

所以 t 等于( |AP | * cosθ ) / |AB | = |AX | / |AB|

垂足X的坐标就可以根据 t, A,B坐标计算：

X = A + t * AB向量

然后得到PX向量

对PQ上每一个点 point 执行 point + PX向量，即完成平移

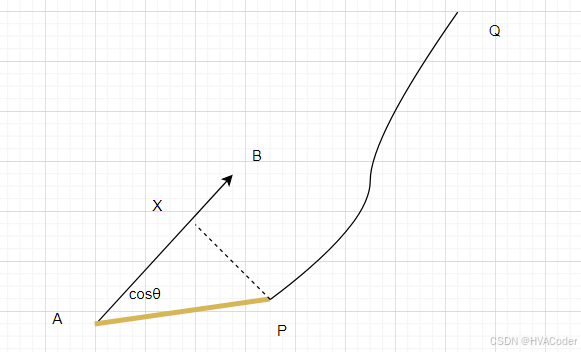
第二种情况，投影在AB外，靠近A的方向, cosθ < 0

t 为负数

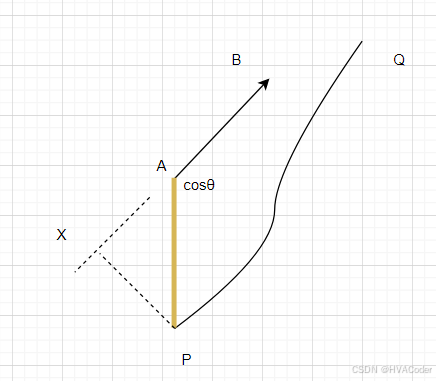
第三种情况，投影在AB外，靠近B的方向，类似的

python代码

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

def normalize_vector(v):
    """单位化向量"""
    norm = np.linalg.norm(v)
    if norm == 0:
        return v
    return v / norm

def point_to_line_distance(point, line_point1, line_point2):
    """
    计算点到直线的距离
    参数:
        point: 点的坐标 (x,y)
        line_point1, line_point2: 直线上的两个点
    返回:
        点到直线的距离
    """
    p = np.array(point)
    p1 = np.array(line_point1)
    p2 = np.array(line_point2)
    
    # 直线方向向量
    line_dir = p2 - p1
    line_length = np.linalg.norm(line_dir)
    
    if line_length < 1e-10:
        # 如果线段长度为零，返回点到点的距离
        return np.linalg.norm(p - p1)
    
    # 计算点到直线的距离
    # 使用向量叉积公式：|(p-p1) × (p2-p1)| / |p2-p1|
    distance = np.abs(np.cross(p2-p1, p-p1)) / line_length
    return distance

def point_to_line_perpendicular_vector(point, line_point1, line_point2):
    """
    计算点到直线的垂线向量
    返回从点到直线的垂线向量（从点指向直线）
    """
    p = np.array(point)
    p1 = np.array(line_point1)
    p2 = np.array(line_point2)
    
    # 直线方向向量
    line_dir = p2 - p1
    line_length_squared = np.dot(line_dir, line_dir)
    
    if line_length_squared < 1e-10:
        return p1 - p
    
    # 计算投影参数 t
    t = np.dot(p - p1, line_dir) / line_length_squared
    
    # 计算垂足坐标
    foot_point = p1 + t * line_dir
    
    # 垂线向量（从点指向垂足）
    perpendicular_vector = foot_point - p
    
    return perpendicular_vector

def translate_curve_by_first_point_distance(line_points, curve_points):
    """
    将曲线沿着线段的垂线方向平移，平移距离等于曲线第一个点到线段的垂直距离
    
    参数:
        line_points: 线段的两个端点 [(x1,y1), (x2,y2)]
        curve_points: 曲线的点集 [(x,y), ...]
    
    返回:
        平移后的曲线点集
    """
    if len(curve_points) == 0:
        return curve_points
    
    # 提取线段端点和曲线第一个点
    p1, p2 = np.array(line_points[0]), np.array(line_points[1])
    first_point = np.array(curve_points[0])
    
    # 计算第一个点到线段的垂线向量
    perp_vector = point_to_line_perpendicular_vector(first_point, p1, p2)
    
    # 计算垂线距离（平移距离）
    distance = np.linalg.norm(perp_vector)
    
    # 计算垂线方向单位向量
    if distance > 1e-10:
        unit_perp = perp_vector / distance
    else:
        # 如果点在直线上，使用法线方向
        line_dir = p2 - p1
        unit_perp = normalize_vector(np.array([line_dir[1], -line_dir[0]]))
    
    # 平移所有曲线点
    translated_points = []
    for point in curve_points:
        new_point = np.array(point) + unit_perp * distance
        translated_points.append(new_point)
    
    return np.array(translated_points), distance

def create_parabola(a, b, c, x_range, num_points=50):
    """创建抛物线点集"""
    x = np.linspace(x_range[0], x_range[1], num_points)
    y = a * x**2 + b * x + c
    return list(zip(x, y))

# 可视化函数
def plot_translation_result(line_points, original_curve, translated_curve, distance, title):
    """绘制平移结果"""
    plt.figure(figsize=(10, 8))
    chinese_fonts = [f.name for f in fm.fontManager.ttflist if 'CJK' in f.name or 'Hei' in f.name or 'YaHei' in f.name]
    print("可用的中文字体:", chinese_fonts)
    # 如果有可用中文字体，使用第一个
    if chinese_fonts:
        plt.rcParams['font.sans-serif'] = [chinese_fonts[0], 'DejaVu Sans']
    else:
        print("未找到中文字体，需要安装")
    # 绘制原始线段
    line_x = [line_points[0][0], line_points[1][0]]
    line_y = [line_points[0][1], line_points[1][1]]
    plt.plot(line_x, line_y, 'b-', linewidth=3, label='参考线段', marker='o', markersize=8)
    
    # 绘制原始曲线
    orig_x, orig_y = zip(*original_curve)
    plt.plot(orig_x, orig_y, 'red', linewidth=2, label='原始曲线')
    plt.scatter(orig_x, orig_y, c='red', s=30, alpha=0.6)
    
    # 绘制平移后的曲线
    trans_x, trans_y = zip(*translated_curve)
    plt.plot(trans_x, trans_y, 'green', linewidth=2, label='平移后曲线')
    plt.scatter(trans_x, trans_y, c='green', s=30, alpha=0.6)
    
    # 标记第一个点并绘制垂线
    first_point = original_curve[0]
    plt.scatter(first_point[0], first_point[1], c='darkred', s=100, marker='*', 
               label='曲线第一个点', zorder=5)
    
    # 计算垂足
    p1, p2 = np.array(line_points[0]), np.array(line_points[1])
    first_pt = np.array(first_point)
    line_dir = p2 - p1
    t = np.dot(first_pt - p1, line_dir) / np.dot(line_dir, line_dir)
    foot_point = p1 + t * line_dir
    
    # 绘制垂线
    plt.plot([first_point[0], foot_point[0]], [first_point[1], foot_point[1]], 
             'purple', linestyle='--', linewidth=2, label=f'垂线 (距离: {distance:.2f})')
    plt.scatter(foot_point[0], foot_point[1], c='blue', s=80, marker='s', label='垂足')
    
    plt.grid(True, alpha=0.3)
    plt.axis('equal')
    plt.legend()
    plt.title(f'{title}\n平移距离: {distance:.2f}')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()

# 示例使用
if __name__ == "__main__":
    print("=== 自适应平移距离测试 ===\n")
    
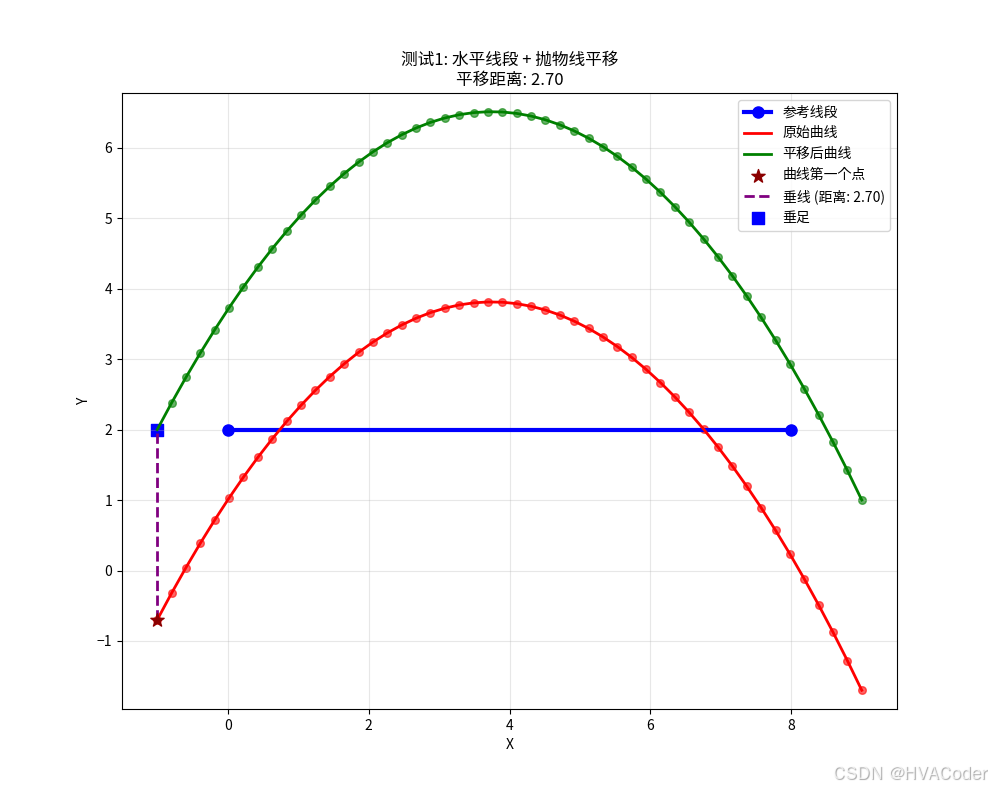
    # 测试1: 水平线段 + 抛物线
    print("测试1: 水平线段 + 抛物线")
    line_segment1 = [(0, 2), (8, 2)]  # 水平线段
    parabola1 = create_parabola(a=-0.2, b=1.5, c=1, x_range=(-1, 9))
    
    translated_parabola1, distance1 = translate_curve_by_first_point_distance(line_segment1, parabola1)
    plot_translation_result(line_segment1, parabola1, translated_parabola1, distance1, 
                           "测试1: 水平线段 + 抛物线平移")
    
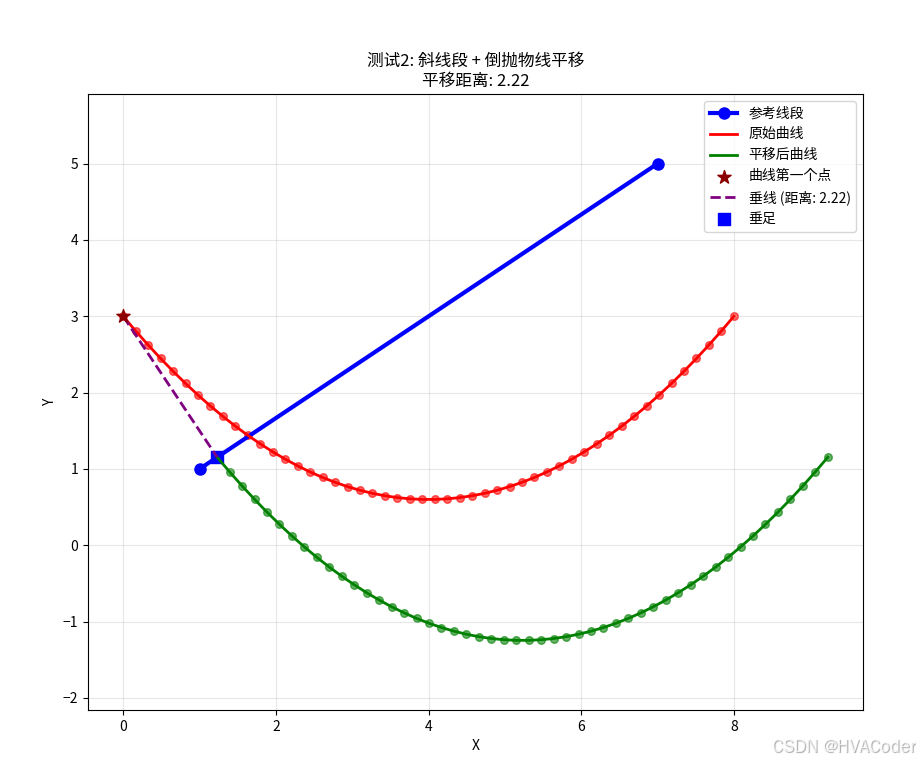
    # 测试2: 斜线段 + 倒抛物线
    print("测试2: 斜线段 + 倒抛物线")
    line_segment2 = [(1, 1), (7, 5)]  # 斜线段
    parabola2 = create_parabola(a=0.15, b=-1.2, c=3, x_range=(0, 8))
    
    translated_parabola2, distance2 = translate_curve_by_first_point_distance(line_segment2, parabola2)
    plot_translation_result(line_segment2, parabola2, translated_parabola2, distance2,
                           "测试2: 斜线段 + 倒抛物线平移")
    
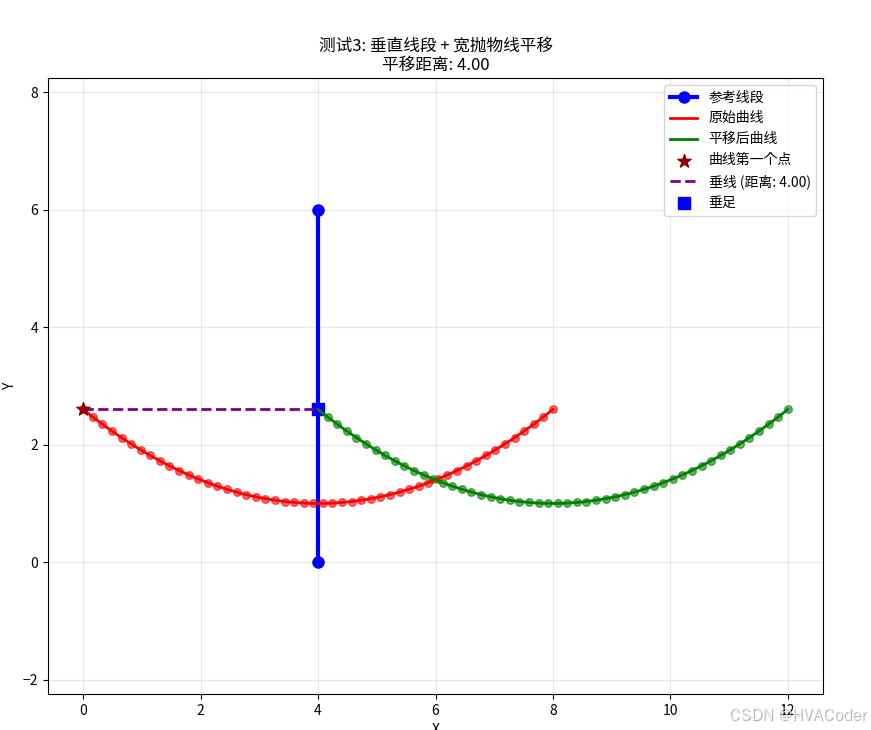
    # 测试3: 垂直线段 + 宽抛物线
    print("测试3: 垂直线段 + 宽抛物线")
    line_segment3 = [(4, 0), (4, 6)]  # 垂直线段
    x3 = np.linspace(0, 8, 50)
    y3 = 0.1 * (x3 - 4)**2 + 1
    parabola3 = list(zip(x3, y3))
    
    translated_parabola3, distance3 = translate_curve_by_first_point_distance(line_segment3, parabola3)
    plot_translation_result(line_segment3, parabola3, translated_parabola3, distance3,
                           "测试3: 垂直线段 + 宽抛物线平移")
    
    # 测试4: 验证平移精度
    print("测试4: 验证平移精度")
    line_segment4 = [(2, 2), (6, 4)]  # 斜线段
    parabola4 = create_parabola(a=0.1, b=-0.5, c=3, x_range=(1, 7))
    
    translated_parabola4, distance4 = translate_curve_by_first_point_distance(line_segment4, parabola4)
    
    # 验证平移后第一个点到线段的距离应该接近0
    first_point_after = translated_parabola4[0]
    new_distance = point_to_line_distance(first_point_after, line_segment4[0], line_segment4[1])
    
    print(f"原始第一个点到线段距离: {distance4:.6f}")
    print(f"平移后第一个点到线段距离: {new_distance:.6f}")
    print(f"平移精度误差: {abs(new_distance):.6f}")
    
    plot_translation_result(line_segment4, parabola4, translated_parabola4, distance4,
                           "测试4: 平移精度验证")
    
    print("\n=== 所有测试完成 ===")

效果可视化