【open3d】示例：自动计算点人脸点云模型面部朝向算法

牙牙要健康2025-12-03 13:36

【open3d】示例：自动计算点人脸点云模型面部朝向算法

文章目录

前言

从点云数据中判断人脸的面部朝向，核心思路是：找到一个能代表面部正方向的向量（通常称为法向量或朝向向量）。

自动估计面部核心区域法向量

核心思想是使用面部核心区域点云的法向量来整体表示面部的朝向。人脸核心区域（脸颊、额头、鼻子）的法向量方向大致相同，都指向面部正前方。

流程详细描述

通过一系列处理步骤来获取一个代表人脸正面方向的单位向量，主要流程如下：

  1. 加载点云数据 ：
    • 从指定的模型文件路径获得三维坐标数据，每行包含x、y、z三个值；
    • 计算点云包围盒对角线长度作为后续自适应参数的基准。
  2. 点云预处理 ：
    • 对点云进行体素下采样，减少数据量；
    • 使用统计滤波去除离群噪声点。
  3. 法向量估计与校正 ：
    • 为每个点计算局部表面法向量；
    • 将所有法向量方向校正为指向人脸外部（远离质心方向）。
  4. 核心区域提取 ：
    • 以点云质心为中心定义球形区域，提取球形区域内的点作为核心区域；
    • 排除边缘区域干扰，只保留面部核心区域，用于后续分析。
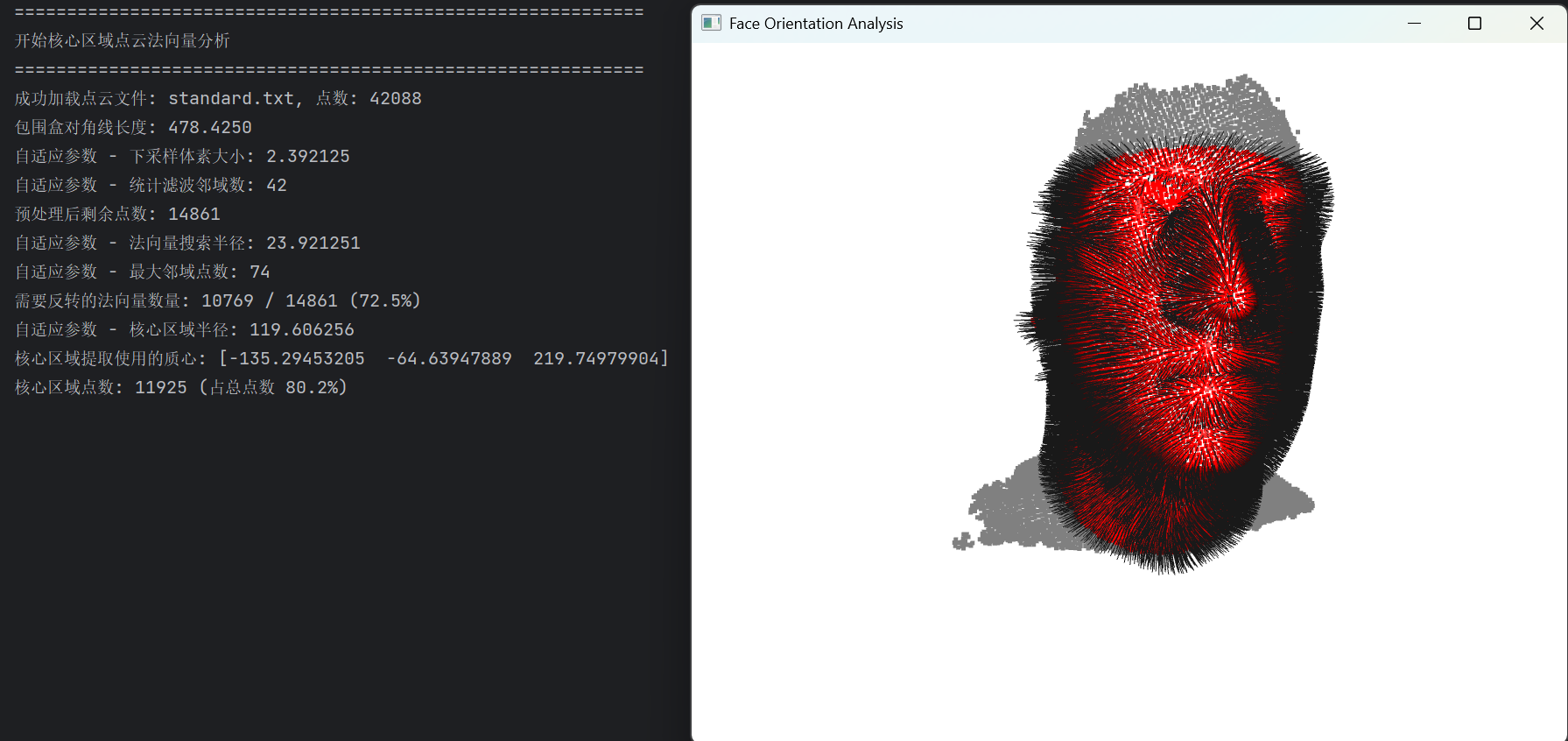
  5. 结果可视化 ：
    • 用灰色显示预处理后的完整点云；
    • 用红色显示核心区域点云；
    • 显示核心区域的法向量，

通过整个流程实现从原始点云数据到面部核心区域法向量的自动计算。

代码详细解析

主流程方法

从数据加载到结果可视化，形成完整闭环。

python 复制代码 
def run_core_analysis(self, filename, voxel_size_ratio=0.005,
                      search_radius_ratio=0.05, core_radius_ratio=0.25):
    # 1. 加载
    self.load_point_cloud_from_txt(filename)
    # 2. 预处理
    self.preprocess_point_cloud(voxel_size_ratio=voxel_size_ratio)
    # 3. 法向量估计
    self.estimate_and_correct_normals(search_radius_ratio=search_radius_ratio)
    # 4. 核心区域提取
    core_pcd = self.extract_core_region(core_radius_ratio=core_radius_ratio)
    # 5. 可视化
    self.visualize_result(core_pcd)

类结构设计

采用了面向对象的设计模式，将相关数据和方法封装在一起，便于管理和复用。

python 复制代码 
class FaceOrientationAnalyzer:
    def __init__(self):
        self.pcd = None            # 存储原始点云
        self.pcd_clean = None      # 存储预处理后的点云
        self.pcd_with_normals = None  # 存储带法向量的点云
        self.core_normals = None   # 存储核心区域法向量
        self.bbox_diag_length = None  # 存储包围盒对角线长度（用于自适应参数）

  1. 数据加载模块

    python 复制代码 
    def load_point_cloud_from_txt(self, filename):
    """从txt文件加载点云数据（每行存储一个点的x,y,z坐标）"""
    try:
        # 从txt文件读取点云数据（默认每行x,y,z）
        points = np.loadtxt(filename)
        if points.ndim != 2 or points.shape[1] != 3:
            raise ValueError("txt文件格式错误，需每行存储x,y,z坐标")

        # 创建Open3D点云对象
        self.pcd = o3d.geometry.PointCloud()
        self.pcd.points = o3d.utility.Vector3dVector(points)

        # 计算包围盒对角线长度（用于自适应参数调整）
        bbox = self.pcd.get_axis_aligned_bounding_box()
        bbox_points = bbox.get_box_points()
        bbox_array = np.asarray(bbox_points)
        self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

        print(f"成功加载点云文件: {filename}, 点数: {len(points)}")
        print(f"包围盒对角线长度: {self.bbox_diag_length:.4f}")
        return self.pcd
    except Exception as e:
        print(f"加载点云文件失败: {e}")
        return None

  2. 点云预处理模块

    python 复制代码 
    def preprocess_point_cloud(self, voxel_size_ratio=0.005):
    """点云预处理：下采样+统计滤波去噪"""
    if self.pcd is None:
        print("请先加载点云数据！")
        return None

    # 自适应计算参数
    voxel_size = self.bbox_diag_length * voxel_size_ratio
    nb_neighbors = max(20, int(len(self.pcd.points) * 0.001))
    std_ratio = 2.0

    print(f"自适应参数 - 下采样体素大小: {voxel_size:.6f}")
    print(f"自适应参数 - 统计滤波邻域数: {nb_neighbors}")

    # 下采样（减少点数，加速计算）
    pcd_down = self.pcd.voxel_down_sample(voxel_size=voxel_size)

    # 统计滤波去噪（去除离群点）
    self.pcd_clean, _ = pcd_down.remove_statistical_outlier(
        nb_neighbors=nb_neighbors,
        std_ratio=std_ratio
    )
    print(f"预处理后剩余点数: {len(self.pcd_clean.points)}")

    return self.pcd_clean

    关键技术点

    自适应参数计算：voxel_size = 对角线长度 × 0.005：体素大小与点云尺寸成正比；nb_neighbors = max(20, 点数的0.1%)：确保最少有20个邻域点。

    voxel_down_sample()体素下采样将空间：划分为体素网格，每个体素内所有点合并为一个点（取平均），大幅减少点数，保持几何特征。

    remove_statistical_outlier()统计滤波：计算每个点到其k个最近邻点的平均距离，假设这些距离服从高斯分布，移除距离均值超过2倍标准差的点，有效去除噪声和离群点。

  3. 法向量估计与校正模块

    python 复制代码 
    def estimate_and_correct_normals(self, search_radius_ratio=0.05):
    """估计法向量并校正为向外（远离质心），自适应参数"""
    if self.pcd_clean is None:
        print("请先预处理点云数据！")
        return None

    # 自适应计算搜索半径
    search_radius = self.bbox_diag_length * search_radius_ratio
    max_nn = max(50, int(len(self.pcd_clean.points) * 0.005))

    print(f"自适应参数 - 法向量搜索半径: {search_radius:.6f}")
    print(f"自适应参数 - 最大邻域点数: {max_nn}")

    # 估计法向量（基于邻域平面拟合）
    self.pcd_clean.estimate_normals(
        search_param=o3d.geometry.KDTreeSearchParamHybrid(
            radius=search_radius,
            max_nn=max_nn
        )
    )

    # 校正法向量方向：确保法向量指向远离质心的方向
    normals = np.asarray(self.pcd_clean.normals)
    points = np.asarray(self.pcd_clean.points)
    centroid = points.mean(axis=0)

    # 计算每个点到质心的向量
    points_to_centroid = points - centroid
    # 点积判断方向：若点积<0，说明法向量指向质心（内部），反转
    dot_product = np.sum(normals * points_to_centroid, axis=1)

    # 统计并显示法向量方向校正情况
    num_reversed = np.sum(dot_product < 0)
    print(f"需要反转的法向量数量: {num_reversed} / {len(normals)} ({100 * num_reversed / len(normals):.1f}%)")

    normals[dot_product < 0] *= -1  # 反转方向
    # 更新点云法向量
    self.pcd_clean.normals = o3d.utility.Vector3dVector(normals)
    self.pcd_with_normals = self.pcd_clean

    return self.pcd_with_normals

    数学原理详解：

    法向量估计：对每个点的邻域进行主成分分析(PCA)，最小特征值对应的特征向量即为法向量方向。

    方向一致性校正：对于凸曲面（如人脸），所有法向量应指向外部；计算法向量 n ⃗ \vec{n} n 与点到质心向量 v ⃗ \vec{v} v 的点积： n ⃗ ⋅ v ⃗ \vec{n} \cdot \vec{v} n ⋅v ，如果 n ⃗ ⋅ v ⃗ < 0 \vec{n} \cdot \vec{v} < 0 n ⋅v <0，说明 n ⃗ \vec{n} n 指向内部，反转这些法向量： n ⃗ = − n ⃗ \vec{n} = -\vec{n} n =−n 。

  4. 核心区域提取模块

    python 复制代码 
       def extract_core_region(self, core_radius_ratio=0.25):
    """提取面部核心区域（排除边缘干扰），自适应参数"""
    if self.pcd_with_normals is None:
        print("请先估计并校正法向量！")
        return None

    # 自适应计算核心区域半径
    core_radius = self.bbox_diag_length * core_radius_ratio
    print(f"自适应参数 - 核心区域半径: {core_radius:.6f}")

    # 使用质心
    centroid = np.asarray(self.pcd_with_normals.points).mean(axis=0)
    print(f"核心区域提取使用的质心: {centroid}")

    points = np.asarray(self.pcd_with_normals.points)

    # 计算每个点到质心的距离（点到质心的欧氏距离）
    distances = np.linalg.norm(points - centroid, axis=1)

    # 提取核心区域
    core_indices = distances < core_radius
    core_points = points[core_indices]
    self.core_normals = np.asarray(self.pcd_with_normals.normals)[core_indices]

    # 统计核心区域信息
    total_points = len(points)
    core_points_count = len(core_points)
    core_ratio = 100 * core_points_count / total_points if total_points > 0 else 0

    print(f"核心区域点数: {core_points_count} (占总点数 {core_ratio:.1f}%)")

    # 创建核心区域点云（用于可视化）
    core_pcd = o3d.geometry.PointCloud()
    core_pcd.points = o3d.utility.Vector3dVector(core_points)
    core_pcd.normals = o3d.utility.Vector3dVector(self.core_normals)

    return core_pcd

    设计思路

    球形区域选择，以点云质心为球心，半径为对角线长度的25%，这个比例适合人脸，能覆盖前额、鼻子、脸颊等核心区域，更能代表面部整体朝向，排除头发耳朵边缘区域干扰。

  5. 可视化模块

    python 复制代码 
    def visualize_result(self, core_pcd):
    """可视化结果：原始点云+核心区域+核心区域法线"""
    if self.pcd_clean is None or core_pcd is None:
        print("数据不完整，无法可视化！")
        return

    # 设置颜色：原始点云灰色，核心区域红色
    self.pcd_clean.paint_uniform_color([0.5, 0.5, 0.5])
    core_pcd.paint_uniform_color([1.0, 0.0, 0.0])

    # 为了只显示核心区域的法线，我们需要将原始点云的法线设置为0
    # 创建一个没有法线的原始点云副本用于可视化
    pcd_no_normals = o3d.geometry.PointCloud()
    pcd_no_normals.points = self.pcd_clean.points
    pcd_no_normals.paint_uniform_color([0.5, 0.5, 0.5])

    # 创建几何体列表
    geometries = [core_pcd,pcd_no_normals]

    o3d.visualization.draw_geometries(
        geometries,
        window_name="Face Orientation Analysis",
        width=1000,
        height=800,
        point_show_normal=True  # 显示法向量（但只有核心点云有法向量）
    )

    显示核心区域法线

完整代码

python 复制代码 
import open3d as o3d
import numpy as np


class FaceOrientationAnalyzer:
    def __init__(self):
        self.pcd = None            # 存储原始点云
        self.pcd_clean = None      # 存储预处理后的点云
        self.pcd_with_normals = None  # 存储带法向量的点云
        self.core_normals = None   # 存储核心区域法向量
        self.bbox_diag_length = None  # 存储包围盒对角线长度（用于自适应参数）

    def load_point_cloud_from_txt(self, filename):
        """从txt文件加载点云数据（每行存储一个点的x,y,z坐标）"""
        try:
            # 从txt文件读取点云数据（默认每行x,y,z）
            points = np.loadtxt(filename)
            if points.ndim != 2 or points.shape[1] != 3:
                raise ValueError("txt文件格式错误，需每行存储x,y,z坐标")

            # 创建Open3D点云对象
            self.pcd = o3d.geometry.PointCloud()
            self.pcd.points = o3d.utility.Vector3dVector(points)

            # 计算包围盒对角线长度（用于自适应参数调整）
            bbox = self.pcd.get_axis_aligned_bounding_box()
            bbox_points = bbox.get_box_points()
            bbox_array = np.asarray(bbox_points)
            self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

            print(f"成功加载点云文件: {filename}, 点数: {len(points)}")
            print(f"包围盒对角线长度: {self.bbox_diag_length:.4f}")
            return self.pcd
        except Exception as e:
            print(f"加载点云文件失败: {e}")
            return None

    def preprocess_point_cloud(self, voxel_size_ratio=0.005):
        """点云预处理：下采样+统计滤波去噪"""
        if self.pcd is None:
            print("请先加载点云数据！")
            return None

        # 自适应计算参数
        voxel_size = self.bbox_diag_length * voxel_size_ratio
        nb_neighbors = max(20, int(len(self.pcd.points) * 0.001))
        std_ratio = 2.0

        print(f"自适应参数 - 下采样体素大小: {voxel_size:.6f}")
        print(f"自适应参数 - 统计滤波邻域数: {nb_neighbors}")

        # 下采样（减少点数，加速计算）
        pcd_down = self.pcd.voxel_down_sample(voxel_size=voxel_size)

        # 统计滤波去噪（去除离群点）
        self.pcd_clean, _ = pcd_down.remove_statistical_outlier(
            nb_neighbors=nb_neighbors,
            std_ratio=std_ratio
        )
        print(f"预处理后剩余点数: {len(self.pcd_clean.points)}")

        return self.pcd_clean

    def estimate_and_correct_normals(self, search_radius_ratio=0.05):
        """估计法向量并校正为向外（远离质心），自适应参数"""
        if self.pcd_clean is None:
            print("请先预处理点云数据！")
            return None

        # 自适应计算搜索半径
        search_radius = self.bbox_diag_length * search_radius_ratio
        max_nn = max(50, int(len(self.pcd_clean.points) * 0.005))

        print(f"自适应参数 - 法向量搜索半径: {search_radius:.6f}")
        print(f"自适应参数 - 最大邻域点数: {max_nn}")

        # 估计法向量（基于邻域平面拟合）
        self.pcd_clean.estimate_normals(
            search_param=o3d.geometry.KDTreeSearchParamHybrid(
                radius=search_radius,
                max_nn=max_nn
            )
        )

        # 校正法向量方向：确保法向量指向远离质心的方向
        normals = np.asarray(self.pcd_clean.normals)
        points = np.asarray(self.pcd_clean.points)
        centroid = points.mean(axis=0)

        # 计算每个点到质心的向量
        points_to_centroid = points - centroid
        # 点积判断方向：若点积<0，说明法向量指向质心（内部），反转
        dot_product = np.sum(normals * points_to_centroid, axis=1)

        # 统计并显示法向量方向校正情况
        num_reversed = np.sum(dot_product < 0)
        print(f"需要反转的法向量数量: {num_reversed} / {len(normals)} ({100 * num_reversed / len(normals):.1f}%)")

        normals[dot_product < 0] *= -1  # 反转方向
        # 更新点云法向量
        self.pcd_clean.normals = o3d.utility.Vector3dVector(normals)
        self.pcd_with_normals = self.pcd_clean

        return self.pcd_with_normals

    def extract_core_region(self, core_radius_ratio=0.25):
        """提取面部核心区域（排除边缘干扰），自适应参数"""
        if self.pcd_with_normals is None:
            print("请先估计并校正法向量！")
            return None

        # 自适应计算核心区域半径
        core_radius = self.bbox_diag_length * core_radius_ratio
        print(f"自适应参数 - 核心区域半径: {core_radius:.6f}")

        # 使用质心
        centroid = np.asarray(self.pcd_with_normals.points).mean(axis=0)
        print(f"核心区域提取使用的质心: {centroid}")

        points = np.asarray(self.pcd_with_normals.points)

        # 计算每个点到质心的距离（点到质心的欧氏距离）
        distances = np.linalg.norm(points - centroid, axis=1)

        # 提取核心区域
        core_indices = distances < core_radius
        core_points = points[core_indices]
        self.core_normals = np.asarray(self.pcd_with_normals.normals)[core_indices]

        # 统计核心区域信息
        total_points = len(points)
        core_points_count = len(core_points)
        core_ratio = 100 * core_points_count / total_points if total_points > 0 else 0

        print(f"核心区域点数: {core_points_count} (占总点数 {core_ratio:.1f}%)")

        # 创建核心区域点云（用于可视化）
        core_pcd = o3d.geometry.PointCloud()
        core_pcd.points = o3d.utility.Vector3dVector(core_points)
        core_pcd.normals = o3d.utility.Vector3dVector(self.core_normals)

        return core_pcd

    def visualize_result(self, core_pcd):
        """可视化结果：原始点云+核心区域+核心区域法线"""
        if self.pcd_clean is None or core_pcd is None:
            print("数据不完整，无法可视化！")
            return

        # 设置颜色：原始点云灰色，核心区域红色
        self.pcd_clean.paint_uniform_color([0.5, 0.5, 0.5])
        core_pcd.paint_uniform_color([1.0, 0.0, 0.0])

        # 为了只显示核心区域的法线，我们需要将原始点云的法线设置为0
        # 创建一个没有法线的原始点云副本用于可视化
        pcd_no_normals = o3d.geometry.PointCloud()
        pcd_no_normals.points = self.pcd_clean.points
        pcd_no_normals.paint_uniform_color([0.5, 0.5, 0.5])

        # 创建几何体列表
        geometries = [core_pcd,pcd_no_normals]
        
        o3d.visualization.draw_geometries(
            geometries,
            window_name="Face Orientation Analysis",
            width=1000,
            height=800,
            point_show_normal=True  # 显示法向量（但只有核心点云有法向量）
        )

    def run_core_analysis(self, filename, voxel_size_ratio=0.005,
                          search_radius_ratio=0.05, core_radius_ratio=0.25):
        """运行简化的核心区域分析流程"""
        print("=" * 60)
        print("开始核心区域点云法向量分析")
        print("=" * 60)

        # 1. 从txt加载点云
        self.load_point_cloud_from_txt(filename)

        # 2. 预处理点云
        self.preprocess_point_cloud(voxel_size_ratio=voxel_size_ratio)

        # 3. 估计并校正法向量
        self.estimate_and_correct_normals(search_radius_ratio=search_radius_ratio)

        # 4. 提取核心区域
        core_pcd = self.extract_core_region(core_radius_ratio=core_radius_ratio)

        # 5. 可视化结果
        self.visualize_result(core_pcd)

        return core_pcd


# ---------------------- 主流程 ----------------------
if __name__ == "__main__":
    # 初始化分析器
    analyzer = FaceOrientationAnalyzer()

    # 使用默认自适应参数运行核心分析
    TXT_PATH = r"standard.txt"  # 替换为你的txt文件路径

    # 运行简化版的核心分析
    core_pcd = analyzer.run_core_analysis(
        filename=TXT_PATH,
        voxel_size_ratio=0.005,  # 下采样体素大小 = 包围盒对角线长度 * 0.005
        search_radius_ratio=0.05,  # 法向量搜索半径 = 包围盒对角线长度 * 0.05
        core_radius_ratio=0.25  # 核心区域半径 = 包围盒对角线长度 * 0.25
    )

算法代码优缺点分析

  1. 优点:
    • 自适应参数，适用于不同尺寸的点云；
    • 模块化设计，易于扩展。
  2. 缺点：
    • 球形核心区域可能不适合极端姿态的人脸；
    • 没有处理点云缺失或不完整的情况。
  3. 扩展方向
    • 面部朝向计算：对核心区域法向量进行PCA分析；
    • 关键点检测：识别鼻尖、眼角等特征点；
    • 姿态估计：计算欧拉角或旋转矩阵。

自动估计面部朝向(主方向)

主要目的是通过点云处理技术自动计算并可视化人脸的朝向。相较于上个小节的版本，这个改进版增加了面部朝向计算功能，实现了从原始点云数据到最终朝向向量的完整分析流程，并能通过3D箭头直观展示面部朝向。

流程详细描述

同样通过一系列处理步骤来获取一个代表人脸正面方向的单位向量，主要流程如下：

  1. 加载点云数据 ：
    • 从指定的模型文件路径获得三维坐标数据，每行包含x、y、z三个值；
    • 计算点云包围盒对角线长度作为后续自适应参数的基准。
  2. 点云预处理 ：
    • 对点云进行体素下采样，减少数据量，提高计算效率；
    • 使用统计滤波去除离群噪声点；
    • 质心中心化：将点云平移到坐标原点。
  3. 法向量估计与校正 ：
    • 为每个点计算局部表面法向量；
    • 将所有法向量方向校正为指向人脸外部（远离质心方向）。
  4. 核心区域提取 ：
    • 以点云质心为中心定义球形区域，提取球形区域内的点作为核心区域；
    • 排除边缘区域干扰，只保留面部核心区域，用于后续分析。
  5. 面部朝向计算 ：
    • 计算核心区域法向量的平均值；
    • 归一化得到单位长度的朝向向量。
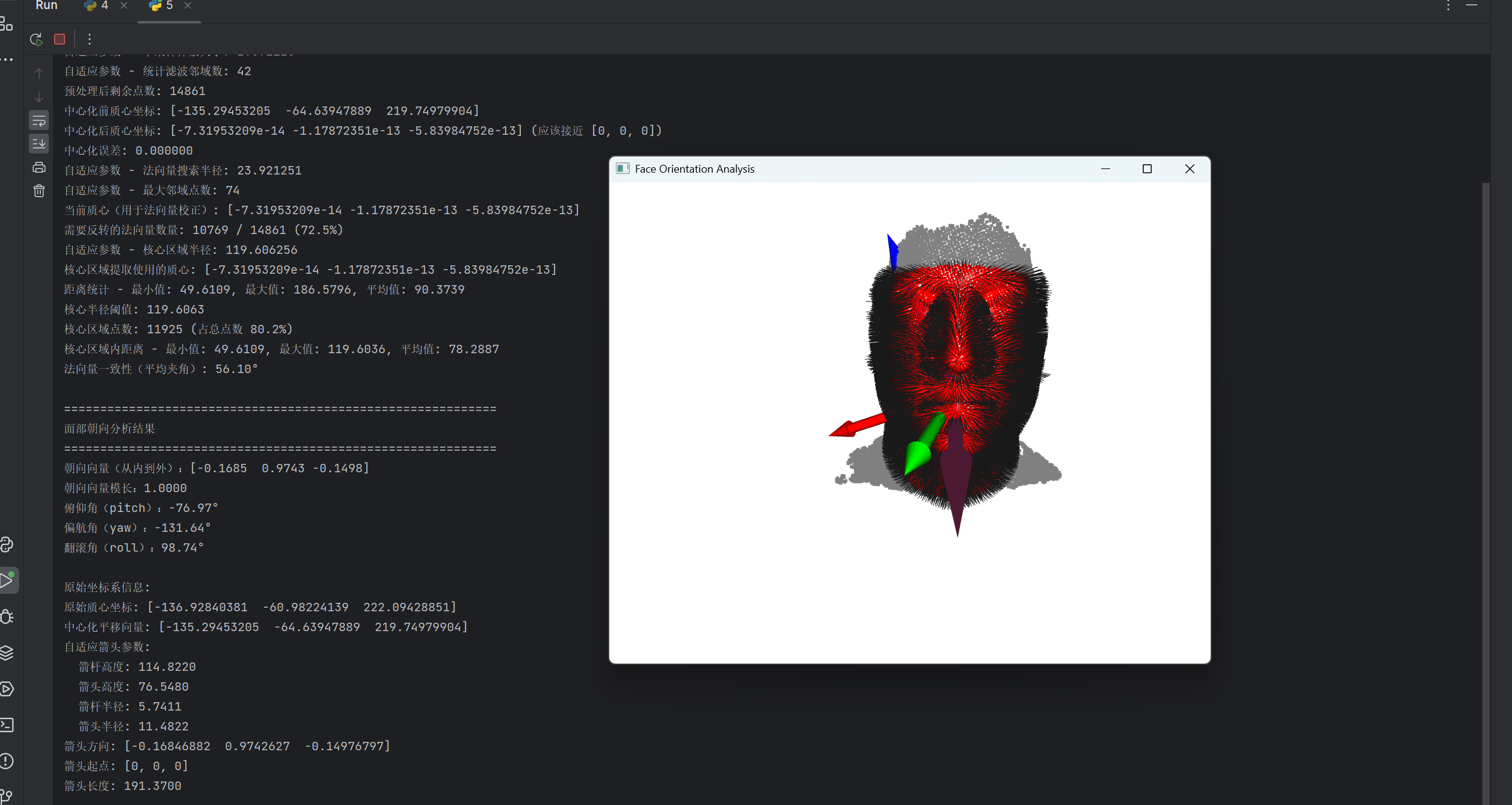
  6. 结果可视化 ：
    • 用灰色显示预处理后的完整点云；
    • 用红色显示核心区域点云；
    • 显示核心区域的法向量；
    • 用蓝色绘制面部朝向箭箭头。

通过整个流程实现从原始点云数据到面部朝向的自动计算。

代码详细解析

类结构设计

延续采用了面向对象的设计模式，将相关数据和方法封装在一起，便于管理和复用。

python 复制代码 
class FaceOrientationAnalyzer:
    def __init__(self):
        # 使用None初始化所有属性，确保安全访问
        self.pcd = None                    # 原始点云
        self.pcd_clean = None              # 预处理后的点云
        self.pcd_with_normals = None       # 带法向量的点云
        self.core_normals = None           # 核心区域法向量
        self.bbox_diag_length = None       # 包围盒对角线长度（关键自适应参数基准）
        self.centroid = None               # 当前质心坐标
        self.original_centroid = None      # 原始质心坐标

  1. 数据加载模块

    python 复制代码 
    def load_point_cloud_from_txt(self, filename):
    """从txt文件加载点云数据（每行存储一个点的x,y,z坐标）"""
    try:
        # 从txt文件读取点云数据（默认每行x,y,z）
        points = np.loadtxt(filename)
        if points.ndim != 2 or points.shape[1] != 3:
            raise ValueError("txt文件格式错误，需每行存储x,y,z坐标")

        # 创建Open3D点云对象
        self.pcd = o3d.geometry.PointCloud()
        self.pcd.points = o3d.utility.Vector3dVector(points)

        # 计算原始质心
        self.original_centroid = points.mean(axis=0)

        # 计算包围盒对角线长度（用于自适应参数调整）
        bbox = self.pcd.get_axis_aligned_bounding_box()
        bbox_points = bbox.get_box_points()
        bbox_array = np.asarray(bbox_points)
        self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

        print(f"成功加载点云文件: {filename}, 点数: {len(points)}")
        print(f"原始质心坐标: {self.original_centroid}")
        print(f"包围盒对角线长度: {self.bbox_diag_length:.4f}")
        return self.pcd
    except Exception as e:
        print(f"加载点云文件失败: {e}")
        return None

  2. 点云预处理模块

    python 复制代码 
    def preprocess_point_cloud(self, voxel_size_ratio=0.005, center=True):
    """点云预处理：下采样+统计滤波去噪，可选质心中心化"""
    if self.pcd is None:
        print("请先加载点云数据！")
        return None

    # 自适应计算参数
    if self.bbox_diag_length is None:
        bbox = self.pcd.get_axis_aligned_bounding_box()
        bbox_points = bbox.get_box_points()
        bbox_array = np.asarray(bbox_points)
        self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

    # 根据包围盒对角线长度计算参数
    voxel_size = self.bbox_diag_length * voxel_size_ratio
    nb_neighbors = max(20, int(len(self.pcd.points) * 0.001))  # 动态调整邻域点数
    std_ratio = 2.0  # 固定值

    print(f"自适应参数 - 下采样体素大小: {voxel_size:.6f}")
    print(f"自适应参数 - 统计滤波邻域数: {nb_neighbors}")

    # 下采样（减少点数，加速计算）
    pcd_down = self.pcd.voxel_down_sample(voxel_size=voxel_size)

    # 统计滤波去噪（去除离群点）
    self.pcd_clean, _ = pcd_down.remove_statistical_outlier(
        nb_neighbors=nb_neighbors,
        std_ratio=std_ratio
    )
    print(f"预处理后剩余点数: {len(self.pcd_clean.points)}")

    # 可选：质心中心化
    if center:
        self.center_point_cloud()

    return self.pcd_clean
 
def center_point_cloud(self):
    """将点云质心平移到原点"""
    if self.pcd_clean is None:
        print("请先预处理点云数据！")
        return None

    # 获取当前点云的质心
    points = np.asarray(self.pcd_clean.points)
    self.centroid = points.mean(axis=0)

    print(f"中心化前质心坐标: {self.centroid}")

    # 将点云平移到原点
    centered_points = points - self.centroid

    # 更新点云
    self.pcd_clean.points = o3d.utility.Vector3dVector(centered_points)

    # 验证中心化结果
    new_points = np.asarray(self.pcd_clean.points)
    new_centroid = new_points.mean(axis=0)
    print(f"中心化后质心坐标: {new_centroid} (应该接近 [0, 0, 0])")
    print(f"中心化误差: {np.linalg.norm(new_centroid):.6f}")

    return self.pcd_clean

    关键技术

    体素下采样：将空间划分为体素网格，每个体素内点合并为一点；

    统计滤波：基于邻域距离分布移除离群点（参数：nb_neighbors邻域点数和std_ratio标准差倍数，2.0表示移除距离均值超过2倍标准差的点）；

    中心化公式： P n e w = P o l d − C P_{new} = P_{old} - C Pnew=Pold−C， C C C是质心坐标，平移后质心应接近原点 ( 0 , 0 , 0 ) (0,0,0) (0,0,0)。

  3. 法向量估计与校正模块

    python 复制代码 
    def estimate_and_correct_normals(self, search_radius_ratio=0.05):
    """估计法向量并校正为向外（远离质心），自适应参数"""
    if self.pcd_clean is None:
        print("请先预处理点云数据！")
        return None

    # 自适应计算搜索半径
    if self.bbox_diag_length is None:
        bbox = self.pcd_clean.get_axis_aligned_bounding_box()
        bbox_points = bbox.get_box_points()
        bbox_array = np.asarray(bbox_points)
        self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

    search_radius = self.bbox_diag_length * search_radius_ratio
    max_nn = max(50, int(len(self.pcd_clean.points) * 0.005))  # 动态调整最大邻域点数

    print(f"自适应参数 - 法向量搜索半径: {search_radius:.6f}")
    print(f"自适应参数 - 最大邻域点数: {max_nn}")

    # 估计法向量（基于邻域平面拟合）
    self.pcd_clean.estimate_normals(
        search_param=o3d.geometry.KDTreeSearchParamHybrid(
            radius=search_radius,
            max_nn=max_nn
        )
    )

    # 计算人脸质心（所有点的均值）
    # 如果已经中心化，质心应该在原点附近
    centroid = np.asarray(self.pcd_clean.points).mean(axis=0)
    print(f"当前质心（用于法向量校正）: {centroid}")

    # 校正法向量方向：确保法向量指向远离质心的方向
    normals = np.asarray(self.pcd_clean.normals)
    points = np.asarray(self.pcd_clean.points)

    # 计算每个点到质心的向量
    points_to_centroid = points - centroid
    # 点积判断方向：若点积<0，说明法向量指向质心（内部），反转
    dot_product = np.sum(normals * points_to_centroid, axis=1)

    # 统计并显示法向量方向校正情况
    num_reversed = np.sum(dot_product < 0)
    print(f"需要反转的法向量数量: {num_reversed} / {len(normals)} ({100 * num_reversed / len(normals):.1f}%)")

    normals[dot_product < 0] *= -1  # 反转方向
    # 更新点云法向量
    self.pcd_clean.normals = o3d.utility.Vector3dVector(normals)
    self.pcd_with_normals = self.pcd_clean
    return self.pcd_with_normals

    算法原理

    法向量估计：对每个点的邻域进行PCA分析，最小特征值对应的特征向量即为法向量。

    方向判断：计算法向量 n ⃗ \vec{n} n 与点到质心向量 v ⃗ \vec{v} v 的点积： n ⃗ ⋅ v ⃗ \vec{n} \cdot \vec{v} n ⋅v ，如果 n ⃗ ⋅ v ⃗ < 0 \vec{n} \cdot \vec{v} < 0 n ⋅v <0，说明 n ⃗ \vec{n} n 指向内部，反转这些法向量： n ⃗ = − n ⃗ \vec{n} = -\vec{n} n =−n 。

  4. 核心区域提取模块

    python 复制代码 
    def extract_core_region(self, core_radius_ratio=0.08):
    """提取面部核心区域（排除边缘干扰），自适应参数"""
    if self.pcd_with_normals is None:
        print("请先估计并校正法向量！")
        return None

    # 自适应计算核心区域半径
    if self.bbox_diag_length is None:
        bbox = self.pcd_with_normals.get_axis_aligned_bounding_box()
        bbox_points = bbox.get_box_points()
        bbox_array = np.asarray(bbox_points)
        self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

    core_radius = self.bbox_diag_length * core_radius_ratio
    print(f"自适应参数 - 核心区域半径: {core_radius:.6f}")

    # 使用当前质心（中心化后应该接近原点）
    centroid = np.asarray(self.pcd_with_normals.points).mean(axis=0)
    print(f"核心区域提取使用的质心: {centroid}")

    points = np.asarray(self.pcd_with_normals.points)

    # 计算每个点到质心的距离
    distances = np.linalg.norm(points - centroid, axis=1)
    # 输出距离统计信息
    print(
        f"距离统计 - 最小值: {distances.min():.4f}, 最大值: {distances.max():.4f}, 平均值: {distances.mean():.4f}")
    print(f"核心半径阈值: {core_radius:.4f}")

    # 提取核心区域
    core_indices = distances < core_radius
    core_points = points[core_indices]
    self.core_normals = np.asarray(self.pcd_with_normals.normals)[core_indices]

    # 统计核心区域信息
    total_points = len(points)
    core_points_count = len(core_points)
    core_ratio = 100 * core_points_count / total_points if total_points > 0 else 0

    print(f"核心区域点数: {core_points_count} (占总点数 {core_ratio:.1f}%)")

    # 显示核心区域内点的距离分布
    if core_points_count > 0:
        core_distances = distances[core_indices]
        print(
            f"核心区域内距离 - 最小值: {core_distances.min():.4f}, 最大值: {core_distances.max():.4f}, 平均值: {core_distances.mean():.4f}")

    # 创建核心区域点云（用于可视化）
    core_pcd = o3d.geometry.PointCloud()
    core_pcd.points = o3d.utility.Vector3dVector(core_points)
    core_pcd.normals = o3d.utility.Vector3dVector(self.core_normals)

    return core_pcd

    筛选出适合人脸核心区域。

  5. 面部朝向计算

    python 复制代码 
    def compute_face_orientation(self):
    """计算最终的面部朝向向量（从内到外）"""
    if self.core_normals is None:
        print("请先提取核心区域！")
        return None

    # 平均法向量并归一化
    avg_normal = self.core_normals.mean(axis=0)
    orientation_vector = avg_normal / np.linalg.norm(avg_normal)

    # 计算法向量一致性（所有核心区域法向量与平均法向量的夹角平均值）
    if len(self.core_normals) > 0:
        # 计算每个法向量与平均法向量的夹角余弦
        cos_angles = np.dot(self.core_normals, orientation_vector) / (
                np.linalg.norm(self.core_normals, axis=1) * np.linalg.norm(orientation_vector)
        )
        # 转换为角度
        angles_deg = np.degrees(np.arccos(np.clip(cos_angles, -1.0, 1.0)))
        consistency = np.mean(angles_deg)
        print(f"法向量一致性（平均夹角）: {consistency:.2f}°")

    return orientation_vector

    数学原理

    归一化： v ⃗ n o r m = v ⃗ ∣ v ⃗ ∣ \vec{v}_{norm} = \frac{\vec{v}}{|\vec{v}|} v norm=∣v ∣v ；

    夹角计算：使用余弦公式 cos ⁡ θ = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ \cos\theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|} cosθ=∣a ∣∣b ∣a ⋅b ；

    一致性评估：平均夹角越小，说明法向量方向越一致，结果越可靠。

  6. 可视化模块

    python 复制代码 
    def visualize_result(self, core_pcd, arrow_scale_factor=0.15):
    """可视化结果：原始点云+核心区域+核心区域法线+朝向箭头"""
    if self.pcd_clean is None or core_pcd is None:
        print("数据不完整，无法可视化！")
        return

    # 设置颜色：原始点云灰色，核心区域红色
    self.pcd_clean.paint_uniform_color([0.5, 0.5, 0.5])
    core_pcd.paint_uniform_color([1.0, 0.0, 0.0])

    # 计算包围盒对角线长度，用于确定箭头大小
    if self.bbox_diag_length is None:
        bbox = self.pcd_clean.get_axis_aligned_bounding_box()
        bbox_points = bbox.get_box_points()
        bbox_array = np.asarray(bbox_points)
        self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

    # 根据模型大小自适应计算箭头参数
    base_size = self.bbox_diag_length * arrow_scale_factor
    cylinder_height = base_size * 0.6  # 箭杆高度
    cone_height = base_size * 0.4  # 箭头高度
    cylinder_radius = base_size * 0.03  # 箭杆半径
    cone_radius = base_size * 0.06  # 箭头半径

    print(f"自适应箭头参数:")
    print(f"  箭杆高度: {cylinder_height:.4f}")
    print(f"  箭头高度: {cone_height:.4f}")
    print(f"  箭杆半径: {cylinder_radius:.4f}")
    print(f"  箭头半径: {cone_radius:.4f}")

    # 创建坐标轴（根据模型大小自适应）
    coordinate_frame = o3d.geometry.TriangleMesh.create_coordinate_frame(
        size=base_size * 0.8,  # 坐标轴大小
        origin=[0, 0, 0]  # 原点
    )

    # 为了只显示核心区域的法线，我们需要将原始点云的法线设置为0
    # 创建一个没有法线的原始点云副本用于可视化
    pcd_no_normals = o3d.geometry.PointCloud()
    pcd_no_normals.points = self.pcd_clean.points
    pcd_no_normals.paint_uniform_color([0.5, 0.5, 0.5])

    # 创建几何体列表
    geometries = [core_pcd, pcd_no_normals, coordinate_frame]

    # 添加朝向箭头（从原点到朝向向量方向）
    if hasattr(self, 'face_orientation'):
        # 创建的箭头默认朝向是 Z 轴正方向
        arrow = o3d.geometry.TriangleMesh.create_arrow(
            cylinder_radius=cylinder_radius,
            cone_radius=cone_radius,
            cylinder_height=cylinder_height,
            cone_height=cone_height
        )

        # 计算旋转矩阵，使箭头指向朝向向量方向
        # 默认箭头是沿着Z轴方向的，所以我们需要计算从Z轴到朝向向量的旋转
        default_direction = np.array([0, 0, 1])  # 默认箭头方向
        R = self._rotation_matrix_from_vectors(default_direction, self.face_orientation)
        arrow.rotate(R, center=[0, 0, 0])

        # 将箭头平移到原点
        arrow.translate([0, 0, 0])
        arrow.paint_uniform_color([0.3, 0.1, 0.2])  # 蓝色箭头

        geometries.append(arrow)

        # 输出箭头信息
        print(f"箭头方向: {self.face_orientation}")
        print(f"箭头起点: [0, 0, 0]")
        print(f"箭头长度: {cylinder_height + cone_height:.4f}")

    o3d.visualization.draw_geometries(
        geometries,
        window_name="Face Orientation Analysis",
        width=1000,
        height=800,
        point_show_normal=True  # 显示法向量（但只有核心点云有法向量）
    )

    辅助函数：用四元数方法计算两个向量之间旋转矩阵的实现。找到一个旋转矩阵 R，使得 R * vec1 = vec2。

    python 复制代码 
    def _rotation_matrix_from_vectors(self, vec1, vec2):
    """使用四元数方法计算旋转矩阵"""

    # 向量归一化:将输入向量标准化为单位长度
    a = vec1 / np.linalg.norm(vec1)
    b = vec2 / np.linalg.norm(vec2)

    # 点积与角度计算
    c = np.dot(a, b)    # a·b = |a||b|cosθ = cosθ (因为都是单位向量)

    if c > 0.999999:  # 相同方向 c ≈ 1
        return np.eye(3)    # 不需要旋转
    elif c < -0.999999:  # 相反方向 c ≈ -1
        # 需要旋转180度
        # 当两个向量方向相反时,有无限多个旋转180度的轴可以选择,任何垂直于vec1的平面内的轴都可以.
        # 选择与a最小分量对应的坐标轴，这样选择的轴与 a 的夹角较大，数值稳定性好
        if abs(a[0]) < abs(a[1]) and abs(a[0]) < abs(a[2]):
            axis = np.array([1, 0, 0])  # 选择x轴
        elif abs(a[1]) < abs(a[2]):
            axis = np.array([0, 1, 0])  # 选择y轴
        else:
            axis = np.array([0, 0, 1])  # 选择z轴

        # 确保轴垂直于vec1（施密特正交化）
        axis = axis - np.dot(axis, a) * a
        axis = axis / np.linalg.norm(axis)
        angle = np.pi
    else:
        axis = np.cross(a, b)   # 叉积得到旋转轴
        axis = axis / np.linalg.norm(axis)  # 归一化
        angle = np.arccos(c)    # 计算夹角

    # 四元数构造
    q = np.array([
        np.cos(angle / 2),      # 标量部分 w
        axis[0] * np.sin(angle / 2),    # 向量部分 x
        axis[1] * np.sin(angle / 2),    # 向量部分 y
        axis[2] * np.sin(angle / 2)     # 向量部分 z
    ])

    # 四元数转旋转矩阵
    q0, q1, q2, q3 = q
    return np.array([
        [1 - 2 * q2 * q2 - 2 * q3 * q3, 2 * q1 * q2 - 2 * q0 * q3, 2 * q1 * q3 + 2 * q0 * q2],
        [2 * q1 * q2 + 2 * q0 * q3, 1 - 2 * q1 * q1 - 2 * q3 * q3, 2 * q2 * q3 - 2 * q0 * q1],
        [2 * q1 * q3 - 2 * q0 * q2, 2 * q2 * q3 + 2 * q0 * q1, 1 - 2 * q1 * q1 - 2 * q2 * q2]
    ])

主流程方法

这个也是类的成员函数：从数据加载到结果可视化，形成完整闭环。

python 复制代码 
def run_full_analysis(self, filename, voxel_size_ratio=0.005, search_radius_ratio=0.05,
                      core_radius_ratio=0.08, center=True, arrow_scale_factor=0.15):
    """运行完整的面部朝向分析流程（包含所有自适应参数）"""
    print("=" * 60)
    print("开始面部朝向分析")
    print("=" * 60)

    # 1. 从txt加载点云
    self.load_point_cloud_from_txt(filename)

    # 2. 预处理点云（包含中心化）
    self.preprocess_point_cloud(voxel_size_ratio=voxel_size_ratio, center=center)

    # 3. 估计并校正法向量
    self.estimate_and_correct_normals(search_radius_ratio=search_radius_ratio)

    # 4. 提取核心区域
    core_pcd = self.extract_core_region(core_radius_ratio=core_radius_ratio)

    # 5. 计算朝向向量
    self.face_orientation = self.compute_face_orientation()

    # 输出结果
    if self.face_orientation is not None:
        print("\n" + "=" * 60)
        print("面部朝向分析结果")
        print("=" * 60)
        print(f"朝向向量（从内到外）：{np.round(self.face_orientation, 4)}")
        print(f"朝向向量模长：{np.linalg.norm(self.face_orientation):.4f}")  # 应为1

        # 计算欧拉角（可选）
        pitch = np.arcsin(-self.face_orientation[1])  # 俯仰角
        yaw = np.arctan2(self.face_orientation[0], self.face_orientation[2])  # 偏航角
        roll = np.arctan2(self.face_orientation[1], self.face_orientation[2])  # 翻滚角
        print(f"俯仰角（pitch）：{np.degrees(pitch):.2f}°")
        print(f"偏航角（yaw）：{np.degrees(yaw):.2f}°")
        print(f"翻滚角（roll）：{np.degrees(roll):.2f}°")

        # 显示原始坐标系下的朝向向量（如果进行了中心化）
        if center and hasattr(self, 'centroid'):
            print(f"\n原始坐标系信息:")
            print(f"原始质心坐标: {self.original_centroid}")
            print(f"中心化平移向量: {self.centroid}")

    # 6. 可视化结果
    self.visualize_result(core_pcd, arrow_scale_factor=arrow_scale_factor)

    return self.face_orientation

欧拉角度定义：

俯仰角（Pitch）：头部上下点头（绕X轴旋转）

偏航角（Yaw）：头部左右摇头（绕Y轴旋转）

翻滚角（Roll）：头部左右倾斜（绕Z轴旋转）

完整代码

python 复制代码 
import open3d as o3d
import numpy as np


class FaceOrientationAnalyzer:
    def __init__(self):
        self.pcd = None
        self.pcd_clean = None
        self.pcd_with_normals = None
        self.core_normals = None
        self.bbox_diag_length = None
        self.centroid = None  # 存储质心坐标
        self.original_centroid = None  # 存储原始质心坐标

    def load_point_cloud_from_txt(self, filename):
        """从txt文件加载点云数据（每行存储一个点的x,y,z坐标）"""
        try:
            # 从txt文件读取点云数据（默认每行x,y,z）
            points = np.loadtxt(filename)
            if points.ndim != 2 or points.shape[1] != 3:
                raise ValueError("txt文件格式错误，需每行存储x,y,z坐标")

            # 创建Open3D点云对象
            self.pcd = o3d.geometry.PointCloud()
            self.pcd.points = o3d.utility.Vector3dVector(points)

            # 计算原始质心
            self.original_centroid = points.mean(axis=0)

            # 计算包围盒对角线长度（用于自适应参数调整）
            bbox = self.pcd.get_axis_aligned_bounding_box()
            bbox_points = bbox.get_box_points()
            bbox_array = np.asarray(bbox_points)
            self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

            print(f"成功加载点云文件: {filename}, 点数: {len(points)}")
            print(f"原始质心坐标: {self.original_centroid}")
            print(f"包围盒对角线长度: {self.bbox_diag_length:.4f}")
            return self.pcd
        except Exception as e:
            print(f"加载点云文件失败: {e}")
            return None

    def center_point_cloud(self):
        """将点云质心平移到原点"""
        if self.pcd_clean is None:
            print("请先预处理点云数据！")
            return None

        # 获取当前点云的质心
        points = np.asarray(self.pcd_clean.points)
        self.centroid = points.mean(axis=0)

        print(f"中心化前质心坐标: {self.centroid}")

        # 将点云平移到原点
        centered_points = points - self.centroid

        # 更新点云
        self.pcd_clean.points = o3d.utility.Vector3dVector(centered_points)

        # 验证中心化结果
        new_points = np.asarray(self.pcd_clean.points)
        new_centroid = new_points.mean(axis=0)
        print(f"中心化后质心坐标: {new_centroid} (应该接近 [0, 0, 0])")
        print(f"中心化误差: {np.linalg.norm(new_centroid):.6f}")

        return self.pcd_clean

    def preprocess_point_cloud(self, voxel_size_ratio=0.005, center=True):
        """点云预处理：下采样+统计滤波去噪，可选质心中心化"""
        if self.pcd is None:
            print("请先加载点云数据！")
            return None

        # 自适应计算参数
        if self.bbox_diag_length is None:
            bbox = self.pcd.get_axis_aligned_bounding_box()
            bbox_points = bbox.get_box_points()
            bbox_array = np.asarray(bbox_points)
            self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

        # 根据包围盒对角线长度计算参数
        voxel_size = self.bbox_diag_length * voxel_size_ratio
        nb_neighbors = max(20, int(len(self.pcd.points) * 0.001))  # 动态调整邻域点数
        std_ratio = 2.0  # 固定值

        print(f"自适应参数 - 下采样体素大小: {voxel_size:.6f}")
        print(f"自适应参数 - 统计滤波邻域数: {nb_neighbors}")

        # 下采样（减少点数，加速计算）
        pcd_down = self.pcd.voxel_down_sample(voxel_size=voxel_size)

        # 统计滤波去噪（去除离群点）
        self.pcd_clean, _ = pcd_down.remove_statistical_outlier(
            nb_neighbors=nb_neighbors,
            std_ratio=std_ratio
        )
        print(f"预处理后剩余点数: {len(self.pcd_clean.points)}")

        # 可选：质心中心化
        if center:
            self.center_point_cloud()

        return self.pcd_clean

    def estimate_and_correct_normals(self, search_radius_ratio=0.05):
        """估计法向量并校正为向外（远离质心），自适应参数"""
        if self.pcd_clean is None:
            print("请先预处理点云数据！")
            return None

        # 自适应计算搜索半径
        if self.bbox_diag_length is None:
            bbox = self.pcd_clean.get_axis_aligned_bounding_box()
            bbox_points = bbox.get_box_points()
            bbox_array = np.asarray(bbox_points)
            self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

        search_radius = self.bbox_diag_length * search_radius_ratio
        max_nn = max(50, int(len(self.pcd_clean.points) * 0.005))  # 动态调整最大邻域点数

        print(f"自适应参数 - 法向量搜索半径: {search_radius:.6f}")
        print(f"自适应参数 - 最大邻域点数: {max_nn}")

        # 估计法向量（基于邻域平面拟合）
        self.pcd_clean.estimate_normals(
            search_param=o3d.geometry.KDTreeSearchParamHybrid(
                radius=search_radius,
                max_nn=max_nn
            )
        )

        # 计算人脸质心（所有点的均值）
        # 如果已经中心化，质心应该在原点附近
        centroid = np.asarray(self.pcd_clean.points).mean(axis=0)
        print(f"当前质心（用于法向量校正）: {centroid}")

        # 校正法向量方向：确保法向量指向远离质心的方向
        normals = np.asarray(self.pcd_clean.normals)
        points = np.asarray(self.pcd_clean.points)

        # 计算每个点到质心的向量
        points_to_centroid = points - centroid
        # 点积判断方向：若点积<0，说明法向量指向质心（内部），反转
        dot_product = np.sum(normals * points_to_centroid, axis=1)

        # 统计并显示法向量方向校正情况
        num_reversed = np.sum(dot_product < 0)
        print(f"需要反转的法向量数量: {num_reversed} / {len(normals)} ({100 * num_reversed / len(normals):.1f}%)")

        normals[dot_product < 0] *= -1  # 反转方向
        # 更新点云法向量
        self.pcd_clean.normals = o3d.utility.Vector3dVector(normals)
        self.pcd_with_normals = self.pcd_clean
        return self.pcd_with_normals

    def extract_core_region(self, core_radius_ratio=0.08):
        """提取面部核心区域（排除边缘干扰），自适应参数"""
        if self.pcd_with_normals is None:
            print("请先估计并校正法向量！")
            return None

        # 自适应计算核心区域半径
        if self.bbox_diag_length is None:
            bbox = self.pcd_with_normals.get_axis_aligned_bounding_box()
            bbox_points = bbox.get_box_points()
            bbox_array = np.asarray(bbox_points)
            self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

        core_radius = self.bbox_diag_length * core_radius_ratio
        print(f"自适应参数 - 核心区域半径: {core_radius:.6f}")

        # 使用当前质心（中心化后应该接近原点）
        centroid = np.asarray(self.pcd_with_normals.points).mean(axis=0)
        print(f"核心区域提取使用的质心: {centroid}")

        points = np.asarray(self.pcd_with_normals.points)

        # 计算每个点到质心的距离
        distances = np.linalg.norm(points - centroid, axis=1)
        # 输出距离统计信息
        print(
            f"距离统计 - 最小值: {distances.min():.4f}, 最大值: {distances.max():.4f}, 平均值: {distances.mean():.4f}")
        print(f"核心半径阈值: {core_radius:.4f}")

        # 提取核心区域
        core_indices = distances < core_radius
        core_points = points[core_indices]
        self.core_normals = np.asarray(self.pcd_with_normals.normals)[core_indices]

        # 统计核心区域信息
        total_points = len(points)
        core_points_count = len(core_points)
        core_ratio = 100 * core_points_count / total_points if total_points > 0 else 0

        print(f"核心区域点数: {core_points_count} (占总点数 {core_ratio:.1f}%)")

        # 显示核心区域内点的距离分布
        if core_points_count > 0:
            core_distances = distances[core_indices]
            print(
                f"核心区域内距离 - 最小值: {core_distances.min():.4f}, 最大值: {core_distances.max():.4f}, 平均值: {core_distances.mean():.4f}")

        # 创建核心区域点云（用于可视化）
        core_pcd = o3d.geometry.PointCloud()
        core_pcd.points = o3d.utility.Vector3dVector(core_points)
        core_pcd.normals = o3d.utility.Vector3dVector(self.core_normals)

        return core_pcd

    def compute_face_orientation(self):
        """计算最终的面部朝向向量（从内到外）"""
        if self.core_normals is None:
            print("请先提取核心区域！")
            return None

        # 平均法向量并归一化
        avg_normal = self.core_normals.mean(axis=0)
        orientation_vector = avg_normal / np.linalg.norm(avg_normal)

        # 计算法向量一致性（所有核心区域法向量与平均法向量的夹角平均值）
        if len(self.core_normals) > 0:
            # 计算每个法向量与平均法向量的夹角余弦
            cos_angles = np.dot(self.core_normals, orientation_vector) / (
                    np.linalg.norm(self.core_normals, axis=1) * np.linalg.norm(orientation_vector)
            )
            # 转换为角度
            angles_deg = np.degrees(np.arccos(np.clip(cos_angles, -1.0, 1.0)))
            consistency = np.mean(angles_deg)
            print(f"法向量一致性（平均夹角）: {consistency:.2f}°")

        return orientation_vector

    def visualize_result(self, core_pcd, arrow_scale_factor=0.15):
        """可视化结果：原始点云+核心区域+核心区域法线+朝向箭头"""
        if self.pcd_clean is None or core_pcd is None:
            print("数据不完整，无法可视化！")
            return

        # 设置颜色：原始点云灰色，核心区域红色
        self.pcd_clean.paint_uniform_color([0.5, 0.5, 0.5])
        core_pcd.paint_uniform_color([1.0, 0.0, 0.0])

        # 计算包围盒对角线长度，用于确定箭头大小
        if self.bbox_diag_length is None:
            bbox = self.pcd_clean.get_axis_aligned_bounding_box()
            bbox_points = bbox.get_box_points()
            bbox_array = np.asarray(bbox_points)
            self.bbox_diag_length = np.linalg.norm(bbox_array.max(axis=0) - bbox_array.min(axis=0))

        # 根据模型大小自适应计算箭头参数
        base_size = self.bbox_diag_length * arrow_scale_factor
        cylinder_height = base_size * 0.6  # 箭杆高度
        cone_height = base_size * 0.4  # 箭头高度
        cylinder_radius = base_size * 0.03  # 箭杆半径
        cone_radius = base_size * 0.06  # 箭头半径

        print(f"自适应箭头参数:")
        print(f"  箭杆高度: {cylinder_height:.4f}")
        print(f"  箭头高度: {cone_height:.4f}")
        print(f"  箭杆半径: {cylinder_radius:.4f}")
        print(f"  箭头半径: {cone_radius:.4f}")

        # 创建坐标轴（根据模型大小自适应）
        coordinate_frame = o3d.geometry.TriangleMesh.create_coordinate_frame(
            size=base_size * 0.8,  # 坐标轴大小
            origin=[0, 0, 0]  # 原点
        )

        # 为了只显示核心区域的法线，我们需要将原始点云的法线设置为0
        # 创建一个没有法线的原始点云副本用于可视化
        pcd_no_normals = o3d.geometry.PointCloud()
        pcd_no_normals.points = self.pcd_clean.points
        pcd_no_normals.paint_uniform_color([0.5, 0.5, 0.5])

        # 创建几何体列表
        geometries = [core_pcd, pcd_no_normals, coordinate_frame]

        # 添加朝向箭头（从原点到朝向向量方向）
        if hasattr(self, 'face_orientation'):
            # 创建的箭头默认朝向是 Z 轴正方向
            arrow = o3d.geometry.TriangleMesh.create_arrow(
                cylinder_radius=cylinder_radius,
                cone_radius=cone_radius,
                cylinder_height=cylinder_height,
                cone_height=cone_height
            )

            # 计算旋转矩阵，使箭头指向朝向向量方向
            # 默认箭头是沿着Z轴方向的，所以我们需要计算从Z轴到朝向向量的旋转
            default_direction = np.array([0, 0, 1])  # 默认箭头方向
            R = self._rotation_matrix_from_vectors(default_direction, self.face_orientation)
            arrow.rotate(R, center=[0, 0, 0])

            # 将箭头平移到原点
            arrow.translate([0, 0, 0])
            arrow.paint_uniform_color([0.3, 0.1, 0.2])  # 蓝色箭头

            geometries.append(arrow)

            # 输出箭头信息
            print(f"箭头方向: {self.face_orientation}")
            print(f"箭头起点: [0, 0, 0]")
            print(f"箭头长度: {cylinder_height + cone_height:.4f}")

        o3d.visualization.draw_geometries(
            geometries,
            window_name="Face Orientation Analysis",
            width=1000,
            height=800,
            point_show_normal=True  # 显示法向量（但只有核心点云有法向量）
        )

    def _rotation_matrix_from_vectors(self, vec1, vec2):
        """计算从vec1到vec2的旋转矩阵"""
        vec1 = vec1 / np.linalg.norm(vec1)
        vec2 = vec2 / np.linalg.norm(vec2)

        # 一般情况下，使用罗德里格斯公式
        v = np.cross(vec1, vec2)
        s = np.linalg.norm(v)
        c = np.dot(vec1, vec2)

        vx = np.array([[0, -v[2], v[1]],
                       [v[2], 0, -v[0]],
                       [-v[1], v[0], 0]])

        R = np.eye(3) + vx + np.dot(vx, vx) * ((1 - c) / (s ** 2))
        return R

    def _rotation_matrix_from_vectors(self, vec1, vec2):
        """使用四元数方法计算旋转矩阵"""

        # 向量归一化:将输入向量标准化为单位长度
        a = vec1 / np.linalg.norm(vec1)
        b = vec2 / np.linalg.norm(vec2)

        # 点积与角度计算
        c = np.dot(a, b)    # a·b = |a||b|cosθ = cosθ (因为都是单位向量)

        if c > 0.999999:  # 相同方向 c ≈ 1
            return np.eye(3)    # 不需要旋转
        elif c < -0.999999:  # 相反方向 c ≈ -1
            # 需要旋转180度
            # 当两个向量方向相反时,有无限多个旋转180度的轴可以选择,任何垂直于vec1的平面内的轴都可以.
            # 选择与a最小分量对应的坐标轴，这样选择的轴与 a 的夹角较大，数值稳定性好
            if abs(a[0]) < abs(a[1]) and abs(a[0]) < abs(a[2]):
                axis = np.array([1, 0, 0])  # 选择x轴
            elif abs(a[1]) < abs(a[2]):
                axis = np.array([0, 1, 0])  # 选择y轴
            else:
                axis = np.array([0, 0, 1])  # 选择z轴

            # 确保轴垂直于vec1（施密特正交化）
            axis = axis - np.dot(axis, a) * a
            axis = axis / np.linalg.norm(axis)
            angle = np.pi
        else:
            axis = np.cross(a, b)   # 叉积得到旋转轴
            axis = axis / np.linalg.norm(axis)  # 归一化
            angle = np.arccos(c)    # 计算夹角

        # 四元数构造
        q = np.array([
            np.cos(angle / 2),      # 标量部分 w
            axis[0] * np.sin(angle / 2),    # 向量部分 x
            axis[1] * np.sin(angle / 2),    # 向量部分 y
            axis[2] * np.sin(angle / 2)     # 向量部分 z
        ])

        # 四元数转旋转矩阵
        q0, q1, q2, q3 = q
        return np.array([
            [1 - 2 * q2 * q2 - 2 * q3 * q3, 2 * q1 * q2 - 2 * q0 * q3, 2 * q1 * q3 + 2 * q0 * q2],
            [2 * q1 * q2 + 2 * q0 * q3, 1 - 2 * q1 * q1 - 2 * q3 * q3, 2 * q2 * q3 - 2 * q0 * q1],
            [2 * q1 * q3 - 2 * q0 * q2, 2 * q2 * q3 + 2 * q0 * q1, 1 - 2 * q1 * q1 - 2 * q2 * q2]
        ])

    def run_full_analysis(self, filename, voxel_size_ratio=0.005, search_radius_ratio=0.05,
                          core_radius_ratio=0.08, center=True, arrow_scale_factor=0.15):
        """运行完整的面部朝向分析流程（包含所有自适应参数）"""
        print("=" * 60)
        print("开始面部朝向分析")
        print("=" * 60)

        # 1. 从txt加载点云
        self.load_point_cloud_from_txt(filename)

        # 2. 预处理点云（包含中心化）
        self.preprocess_point_cloud(voxel_size_ratio=voxel_size_ratio, center=center)

        # 3. 估计并校正法向量
        self.estimate_and_correct_normals(search_radius_ratio=search_radius_ratio)

        # 4. 提取核心区域
        core_pcd = self.extract_core_region(core_radius_ratio=core_radius_ratio)

        # 5. 计算朝向向量
        self.face_orientation = self.compute_face_orientation()

        # 输出结果
        if self.face_orientation is not None:
            print("\n" + "=" * 60)
            print("面部朝向分析结果")
            print("=" * 60)
            print(f"朝向向量（从内到外）：{np.round(self.face_orientation, 4)}")
            print(f"朝向向量模长：{np.linalg.norm(self.face_orientation):.4f}")  # 应为1

            # 计算欧拉角（可选）
            pitch = np.arcsin(-self.face_orientation[1])  # 俯仰角
            yaw = np.arctan2(self.face_orientation[0], self.face_orientation[2])  # 偏航角
            roll = np.arctan2(self.face_orientation[1], self.face_orientation[2])  # 翻滚角
            print(f"俯仰角（pitch）：{np.degrees(pitch):.2f}°")
            print(f"偏航角（yaw）：{np.degrees(yaw):.2f}°")
            print(f"翻滚角（roll）：{np.degrees(roll):.2f}°")

            # 显示原始坐标系下的朝向向量（如果进行了中心化）
            if center and hasattr(self, 'centroid'):
                print(f"\n原始坐标系信息:")
                print(f"原始质心坐标: {self.original_centroid}")
                print(f"中心化平移向量: {self.centroid}")

        # 6. 可视化结果
        self.visualize_result(core_pcd, arrow_scale_factor=arrow_scale_factor)

        return self.face_orientation


# ---------------------- 主流程 ----------------------
if __name__ == "__main__":
    # 初始化分析器
    analyzer = FaceOrientationAnalyzer()

    # 使用默认自适应参数运行完整分析
    TXT_PATH = r"standard.txt"  # 替换为你的txt文件路径

    # 方法1：使用run_full_analysis一键运行（推荐）
    face_orientation = analyzer.run_full_analysis(
        filename=TXT_PATH,
        voxel_size_ratio=0.005,  # 下采样体素大小 = 包围盒对角线长度 * 0.005
        search_radius_ratio=0.05,  # 法向量搜索半径 = 包围盒对角线长度 * 0.05
        core_radius_ratio=0.25,  # 核心区域半径 = 包围盒对角线长度 * 0.08
        center=True,  # 是否进行质心中心化
        arrow_scale_factor=0.4  # 箭头缩放因子 = 包围盒对角线长度 * 0.15
    )

棕色箭头就是人脸朝向方向。

算法代码优缺点分析

  1. 优点:
    • 自适应性强：所有参数基于点云尺寸自动调整；
    • 鲁棒性好：通过核心区域提取排除边缘干扰。
  2. 缺点：
    • 球形核心假设：假设人脸核心区域是球形的，可能不适合极端姿态；
    • 法向量一致性：如果人脸有表情变化，法向量可能不一致；
    • 没有关键点检测：未使用眼睛、鼻子等关键点精化结果。
  3. 扩展方向
    • 添加关键点检测：结合眼睛、鼻子位置精化朝向估计；
    • 多方法融合：结合PCA分析和法向量平均；
    • 姿态分类：根据欧拉角分类正脸、侧脸等。

总结

完成了通过点云处理技术自动计算人脸面部朝向的简单算法。

相关推荐
小李小李快乐不已28 分钟前
图论理论基础（3）
数据结构·c++·算法·图论
lalala_lulu29 分钟前
Lambda表达式是什么
开发语言·python
hxj..29 分钟前
AI发展史介绍
人工智能
科普瑞传感仪器29 分钟前
基于六维力传感器的机器人柔性装配，如何提升发动机零部件装配质量？
java·前端·人工智能·机器人·无人机
youngee1130 分钟前
hot100-41二叉搜索树中第K小的元素
算法
r***869834 分钟前
Python中的简单爬虫
爬虫·python·信息可视化
胡乱儿起个名36 分钟前
Qwen2模型架构
人工智能·深度学习
龙亘川38 分钟前
2025 年中国养老机器人行业全景分析：技术演进、市场格局与商业化路径
大数据·人工智能·机器人
i查拉图斯特拉如是39 分钟前
搭建本地大模型知识库
人工智能·ai·大模型·知识库·ollama
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04BongoCat - 跨平台键盘猫动画工具05本地部署阿里最新开源的Z-Image06Linux下V2Ray安装配置指南07【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）08Meta第三代“分割一切”模型——SAM 3本地部署教程：首支持文本提示分割，400万概念、30毫秒响应，检测分割追踪一网打尽09【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连10Labelme从安装到标注：零基础完整指南