目录
[1. 二叉树创建字符串](#1. 二叉树创建字符串)
[2. 二叉树的层序遍历](#2. 二叉树的层序遍历)
[3. 二叉树的最近公共祖先](#3. 二叉树的最近公共祖先)
[优化到 O(N)](#优化到 O(N))
[4. 二叉搜索树转化为有序双向链表](#4. 二叉搜索树转化为有序双向链表)
[5. 按前序、中序遍历构造二叉树](#5. 按前序、中序遍历构造二叉树)
[6. 非递归 · 前序](#6. 非递归 · 前序)
[7. 非递归 · 中序](#7. 非递归 · 中序)
[8. 非递归 · 后序](#8. 非递归 · 后序)
1. 二叉树创建字符串
606. 根据二叉树创建字符串 - 力扣（LeetCode）
cpp
class Solution {
public:
string tree2str(TreeNode* root) {
}
};用前序遍例
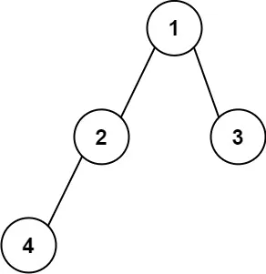输出："1(2(4))(3)" 简化前："1(2(4)()())(3()())"
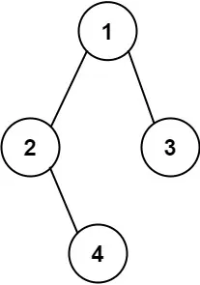输出："1(2()(4))(3)"
**思路：**前序遍例（根、左、右）
1. 左空，右不空：左括号保留
2. 左不空，右空：右括号删
3. 左空，右空：左右括号都删
cpp
class Solution {
public:
string tree2str(TreeNode* root) {
string str;
if (root == nullptr)
return str;
str += to_string(root->val);
if (root->left || root->right)
{
str += '(';
str += tree2str(root->left);
str += ')';
}
if (root->right)
{
str += '(';
str += tree2str(root->right);
str += ')';
}
return str;
}
};第10行的写法非常经典：判断是否往左递归，录值或保留左括号
左不空：往左递归，录值
左空，右不空：往左递归，以保留左括号
左空，右空：不需要保留左括号
再到第17行：
右不为空：录值
右为空：不保留右括号
2. 二叉树的层序遍历
cpp
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
}
};广度优先遍历想到 queue
以前的层序遍历光让把数据打印出来，用一个队列：出一个节点并打印、入它的俩娃，直至队列为空
这道题不一样，要求一层一层遍历，并把每一层放到二维数组的每一行
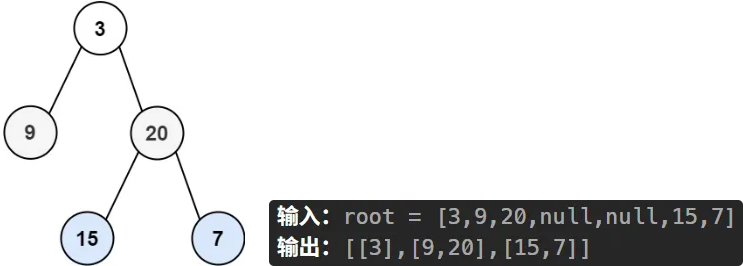
**思路1：**双队列，一个存节点，一个记录行数
**思路2：**用 levelSize 控制层数，一层一层出
以前：
cpp
while (!empty(q))
{
TreeNode* front = q.front();
q.pop();
if (front->left)
q.push(front->left);
if (front->right)
q.push(front->right);
}队列中最多有两层的数据，以前每出一个，不知道出的在哪一层
现在：
cpp
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
queue<TreeNode*> q;
int levelSize = 0;
if (root)
{
q.push(root);
levelSize = 1;
}
while (!q.empty())
{
vector<int> v;
for (int i = 0; i < levelSize; i++)
{
TreeNode* front = q.front();
v.push_back(front->val);
q.pop();
if (front->left)
q.push(front->left);
if (front->right)
q.push(front->right);
}
vv.push_back(v);
levelSize = q.size();
}
return vv;
}
};
原本 levelSize = 1，把 3 出了，levelSize = 2，就知道再往下的俩数据是一层
**二叉树的层序遍历II：**自底向上层层遍历，放到二维数组
107. 二叉树的层序遍历 II - 力扣（LeetCode）
这样即可：
cpp
reverse(vv.begin(), vv.end());
return vv;3. 二叉树的最近公共祖先
236. 二叉树的最近公共祖先 - 力扣（LeetCode）
cpp
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
}
};树中所有节点的值都不相同，一个节点的祖先可以是自己
找 p q 俩节点的最近公共祖先 x p != q 且 都在二叉树中
思路：
A 链表相交类似问题
a 三叉链 （存父节点）O(N)
b 用栈找路径 O(N)
B 普通解法：
a 普通二叉树：通过查找函数，确定节点在左（右）树 O(N^2)
1. 若当前根就是 p 或 q 节点，则当前根为最近公共祖先
2. 若 p q 节点，一个在左树、一个在右树，则当前根为最近公共祖先
3. 若 p q 节点，都在左（右）树，则递归去左（右）树找，直至满足 1 2 的条件
b 二叉搜索树 ： 通过比较大小 ，确定节点在左（右）树 O(N)
cpp
class Solution {
public:
bool Find(TreeNode* tree, TreeNode* x)
{
if (tree == nullptr)
return false;
return tree == x
|| Find(tree->left, x)
|| Find(tree->right, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr)
return nullptr;
if (root == p || root == q)
return root;
bool pleft, pright, qleft, qright;
pleft = Find(root->left, p);
pright = !pleft;
qleft = Find(root->left, q);
qright = !qleft;
if (pleft && qleft)
return lowestCommonAncestor(root->left, p, q);
else if (pright && qright)
return lowestCommonAncestor(root->right, p, q);
else
return root;
}
};20 - 25行很巧妙：
如果 p 在左，Find 能找到，pleft 是真，pright 自动为假
如果 p 在右，Find 找不到，pleft 是假，pright 自动为真
这样写，时间复杂度是 O(N^2)
从 root 开始，每层往下走等差数列次 ↓
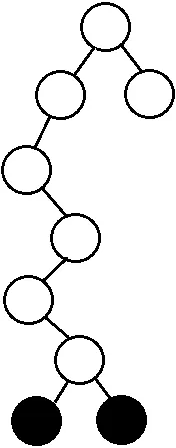
优化到 O(N)
查找过程 + 栈，就能在普通二叉树里搞定节点的路径，存到栈里
遇到不相等的节点也要入栈，因为不确定这个节点在不在路径上
要用节点比较，不能用值比较，可能有相同的值
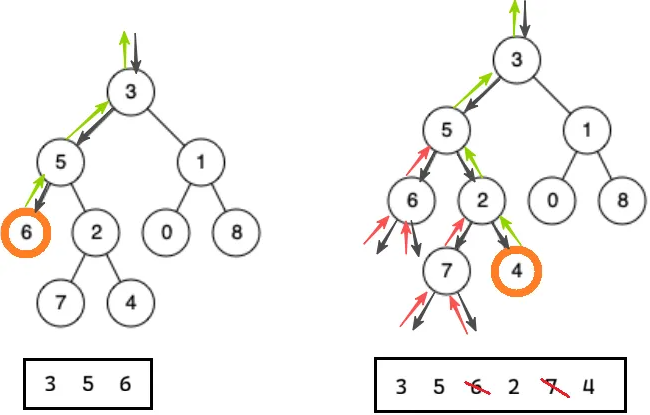
递归全程是在一个栈上入、删数据的，所以 path 引用传参
节点先入栈，在该节点构成的子树中找 x**（找的顺序：根、左子树、右子树）**
找到了（10-17 行）：该节点在 x 的路径上
没找到（到第 19 行）：该节点不在 x 的路径上，出栈
cpp
class Solution {
public:
bool FindPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
{
if (root == nullptr)
return false;
path.push(root);
if (root == x)
return true;
if (FindPath(root->left, x, path))
return true;
if (FindPath(root->right, x, path))
return true;
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pPath, qPath;
FindPath(root, p, pPath);
FindPath(root, q, qPath);
while (pPath.size() > qPath.size())
{
pPath.pop();
}
while (pPath.size() < qPath.size())
{
qPath.pop();
}
while (pPath.top() != qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
};4. 二叉搜索树转化为有序双向链表
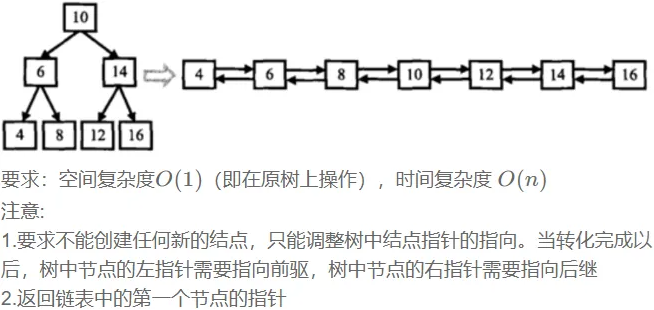
cpp
#include <cstddef>
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree) {
}
};说了二叉搜索树、有序：中序遍历
先写个中序遍历的框架，再不断往里面加东西
要找到当前根的左娃（前一个节点）、右娃（后一个节点），连接起来，所以要传 prev
上面栈帧的 prev 要用下面栈帧的 prev ，来确保连接关系，所以prev 要传引用 ， 确保整个代码中只有一个 prev
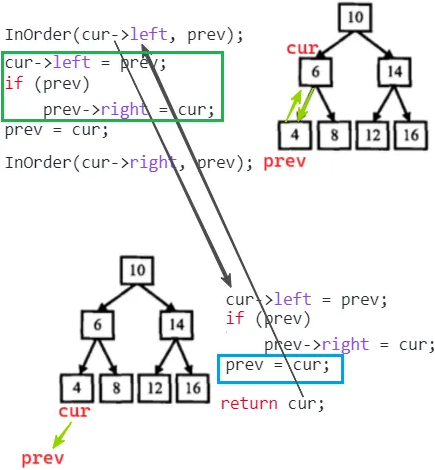
下面的栈帧里改变了 prev，并且上面的栈帧要利用这次改变，prev 就要传引用或二级指针
站在当前节点，找左娃（前一个节点）很容易实现；找右娃（后一个节点）根本实现不了，怎么能预测明天的事呢
换个思路：当前节点能和左娃（前一个节点）链接，左娃（前一个节点）就能和当前节点链接
cpp
#include <cstddef>
class Solution {
public:
void InOrder(TreeNode* cur, TreeNode*& prev)
{
if (cur == nullptr)
return;
InOrder(cur->left, prev);
// 当前节点的left指向前一个
cur->left = prev;
// 前一个节点的right指向当前节点（链接上了）
if (prev)
prev->right = cur;
prev = cur;
InOrder(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
TreeNode* prev = nullptr;
InOrder(pRootOfTree, prev);
TreeNode* head = pRootOfTree;
while (head && head->left)
{
head = head->left;
}
return head;
}
};5. 按前序、中序遍历构造二叉树
105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）
cpp
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
}
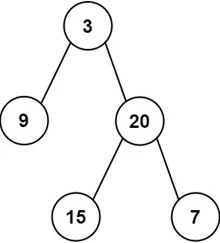
};前序： 根 左子树 右子树 确定根
中序： 左子树 根 右子树 确定左右子树，分割左右区间
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
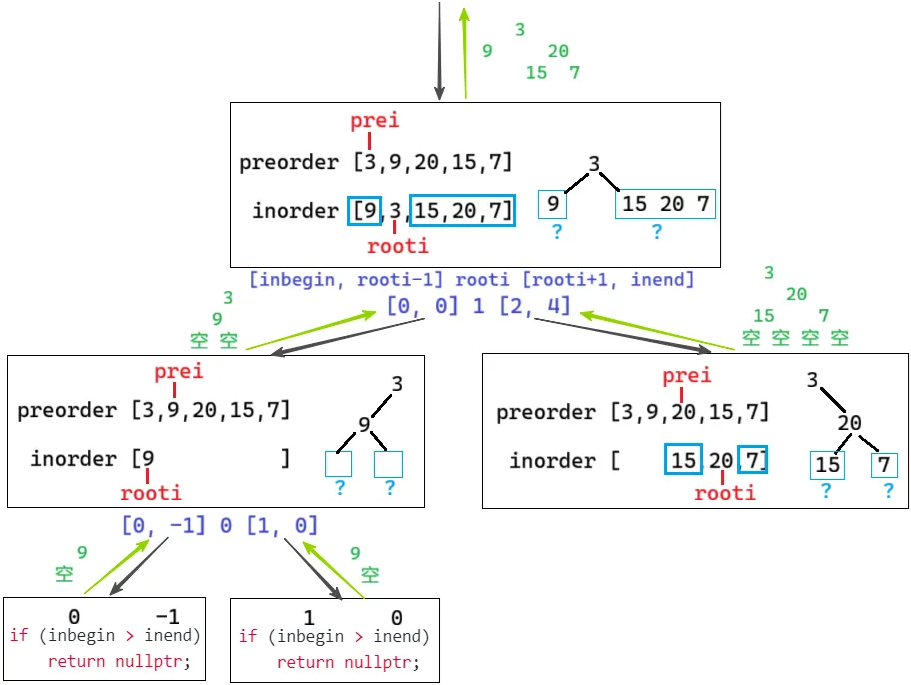
cpp
class Solution {
public:
TreeNode* _build(vector<int>& preorder, vector<int>& inorder,
int& prei, int inbegin, int inend)
{
if (inbegin > inend)
return nullptr;
TreeNode* root = new TreeNode(preorder[prei]);
// 找中序的分割区间
int rooti = inbegin;
while (rooti <= inend)
{
if (preorder[prei] == inorder[rooti])
break;
rooti++;
}
// prei创节点、找分割区间的任务完成了
// [inbegin, rooti-1] rooti [rooti+1, inend]
// 开始递归
++prei;
root->left = _build(preorder, inorder, prei, inbegin, rooti - 1);
root->right = _build(preorder, inorder, prei, rooti + 1, inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int i = 0;
return _build(preorder, inorder, i, 0, preorder.size() - 1);
}
};按中序、后序遍历构造二叉树
https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/
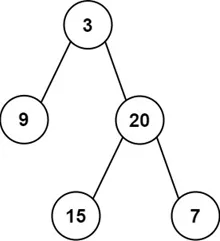
后序最后一个确定根，倒着来，先构建右子树
如果右树不为空，后序的下一个值就是右子树的根
inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]
cpp
class Solution {
public:
TreeNode* _build(vector<int>& inorder, vector<int>& postorder,
int& posti, int inbegin, int inend)
{
if (inbegin > inend)
return nullptr;
// 创建根节点
TreeNode* root = new TreeNode(postorder[posti]);
// 分割中序左右区间
int rooti = inend;
while (inbegin <= rooti)
{
if (postorder[posti] == inorder[rooti])
break;
--rooti;
}
// posti使命完成
// [inbegin, rooti-1] rooti [rooti+1, inend]
--posti;
root->right = _build(inorder, postorder, posti, rooti + 1, inend);
root->left = _build(inorder, postorder, posti, inbegin, rooti - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int i = postorder.size() - 1;
return _build(inorder, postorder, i, 0, i);
}
};按前序、后序不能重建二叉树，分割不出左子树右子树
6. 非递归 · 前序
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
}
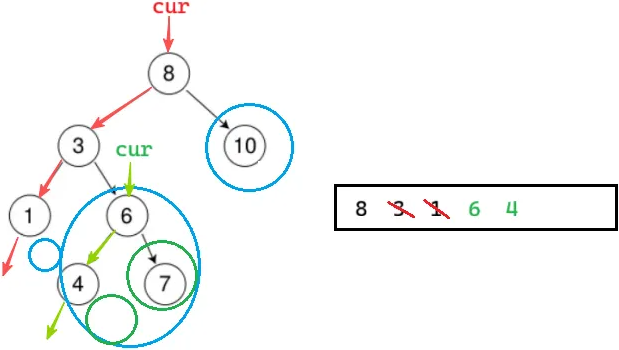
};前序遍历刚开始肯定是把左边一路节点遍历，所以可以这么看一颗二叉树：
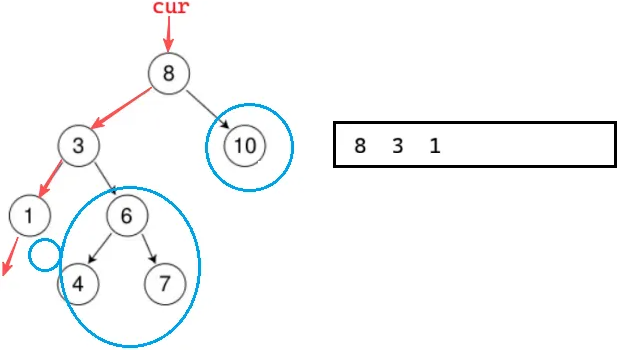
1. cur 指向一颗节点，意味着要访问它的右子树
2. 栈里的节点，意味着要访问它的右子树
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur || !st.empty())
{
// 访问一颗树的开始
// 访问左路节点，左路节点入栈，后续依次访问左路节点的右子树
while (cur)
{
v.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
// 依次访问左路节点的右子树
TreeNode* top = st.top();
st.pop();
// 子问题的方式访问右子树
cur = top->right;
}
return v;
}
};7. 非递归 · 中序
前序遍历，左路节点入栈时访问；中序遍历只是节点访问时机不同
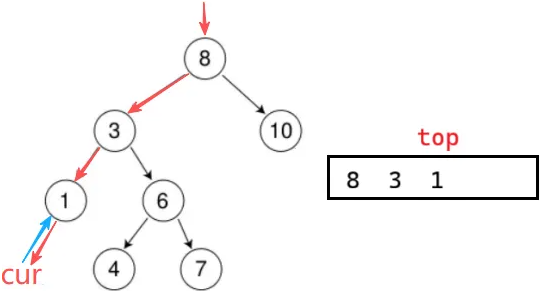
思路：
1. 左路节点入栈
2. 访问左路节点、左路节点右子树
左路节点入完时， ++此时栈顶 top 指向 1，cur 指向 1 的左，cur == nullptr，不用访问（1 的左已经访问，可以访问 1 这个节点了）++，访问它；再访问 1 的右子树
本质：从栈里取到栈顶节点，则这个节点的左子树已经访问完了，可以访问节点、右子树了
cpp
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur || !st.empty())
{
// 左路节点入栈，后续依次访问左路节点、右子树
while (cur)
{
st.push(cur);
cur = cur->left;
}
// 访问左路节点
TreeNode* top = st.top();
st.pop();
v.push_back(top->val);
// 访问右子树
cur = top->right;
}
return v;
}
};8. 非递归 · 后序
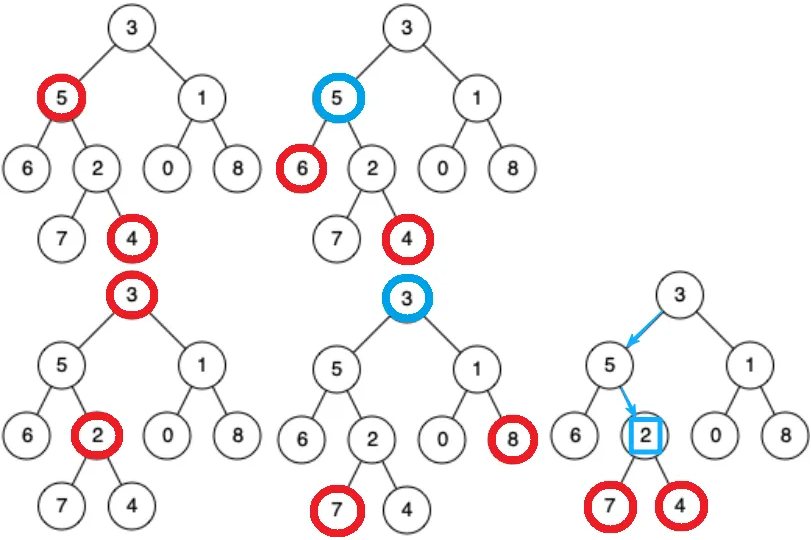
右子树访问完，才能访问根
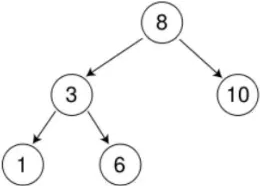
右不为空，怎么识别能不能访问 3 这个节点？
怎么知道是第一次访问 3 的右，还是 3 的右已经访问过了，避免死循环
如果 3 的右子树没有访问过，上一个访问的节点是****左子树的根 1
如果 3 的右子树访问过，上一个访问的节点是****右子树的根 6
一个节点右子树为空，或上一个访问的节点是右子树的根，则说明右子树访问过了，可以访问当前根节点
本质：从栈里取到栈顶节点，则这个节点的左子树已经访问完了
cpp
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while (cur || !st.empty())
{
// 左路节点入栈
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
// 能不能访问这个节点？有2个标志
if (top->right == nullptr || top->right == prev)
{
prev = top;
v.push_back(top->val);
st.pop();
}
else // 不能访问这个节点，要先访问它的右子树
{
cur = top->right;
}
}
return v;
}
};本篇的分享就到这里了，感谢观看 ，如果对你有帮助，别忘了点赞+收藏+关注 。
小编会以自己学习过程中遇到的问题为素材，持续为您推送文章