学习来源:
图神经网络(1)_图论基础
图神经网络(2)_图的表示
文章目录
- [1. 图论基础](#1. 图论基础)
-
- [1.1 图(Graph)的定义](#1.1 图(Graph)的定义)
- [1.2 图的常见类型](#1.2 图的常见类型)
-
- [1.2.1 无向图、有向图](#1.2.1 无向图、有向图)
- [1.2.2 无权图、有权图](#1.2.2 无权图、有权图)
- [1.2.3 同构图、异构图](#1.2.3 同构图、异构图)
- [1.3 图的表示](#1.3 图的表示)
-
- [1.3.1 【例】邻接矩阵](#1.3.1 【例】邻接矩阵)
- [1.3.2 【例】邻接列表](#1.3.2 【例】邻接列表)
- [1.3.3 【例】边集](#1.3.3 【例】边集)
- [1.4 邻居、度](#1.4 邻居、度)
- [1.5 结构特征、节点特征、边特征](#1.5 结构特征、节点特征、边特征)
1. 图论基础
1.1 图(Graph)的定义
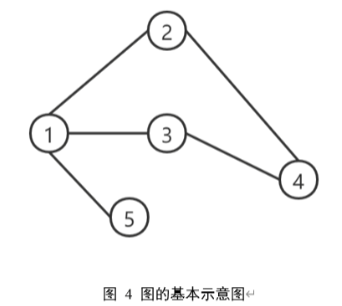
一个图 G 由两个集合组成:G=(V,E)
V:节点集合(Vertices),表示节点,比如人、分子中的原子、论文等。
E:边集合(Edges),表示节点之间的关系,比如社交网络中的"好友关系"、分子中的"化学键"、论文之间的"引用关系"。
1.2 图的常见类型
1.2.1 无向图、有向图
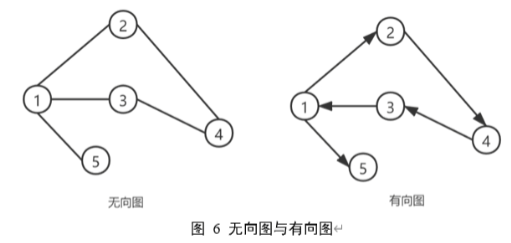
无向图:边没有方向,表示对称关系(如朋友关系)。等价于双向有向图
有向图:边有方向,表示非对称关系(如微博关注)
特例:有向有环图、有向无环图
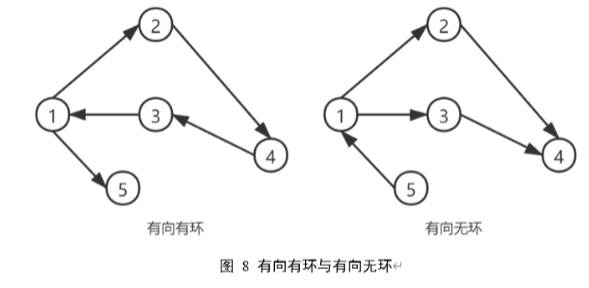
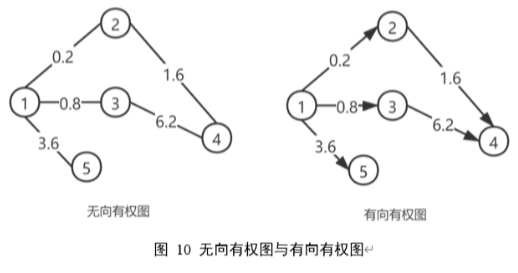
1.2.2 无权图、有权图
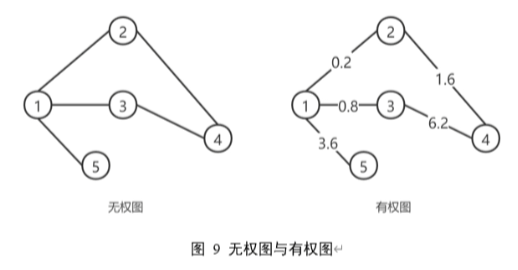
无权图:边无权重
有权图:边有权重,表示关系的强度(如交通路网中的距离)
1.2.3 同构图、异构图
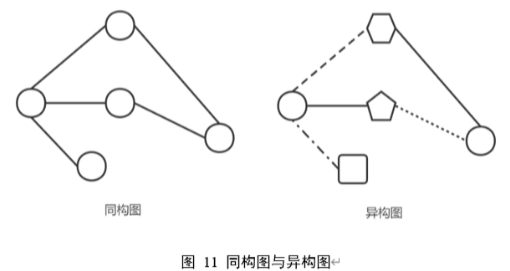
同构图:节点和边只有1种类型
异构图:节点和边有多种类型(如用户-商品-标签图)
1.3 图的表示
| 表示方法 | 说明 |
|---|---|
| 邻接矩阵 | 一个 n × n n \times n n×n 的矩阵 A A A, A i j = 1 A_{ij} = 1 Aij=1 表示节点 i i i 和 j j j 之间有边 |
| 邻接列表 | 每个节点维护一个列表,记录它连接的邻居节点 |
| 边集 | 用一个列表存储所有边,如 ( u , v ) (u, v) (u,v) 表示一条边 |
1.3.1 【例】邻接矩阵
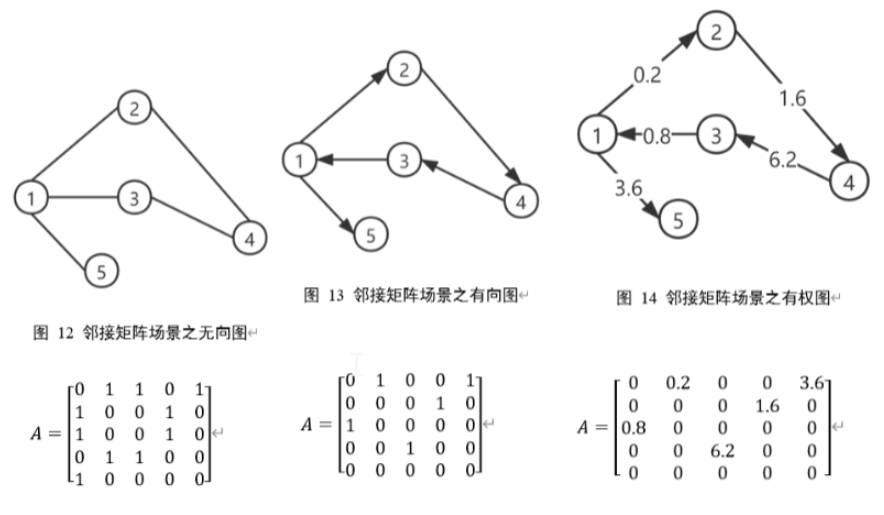
1.3.2 【例】邻接列表
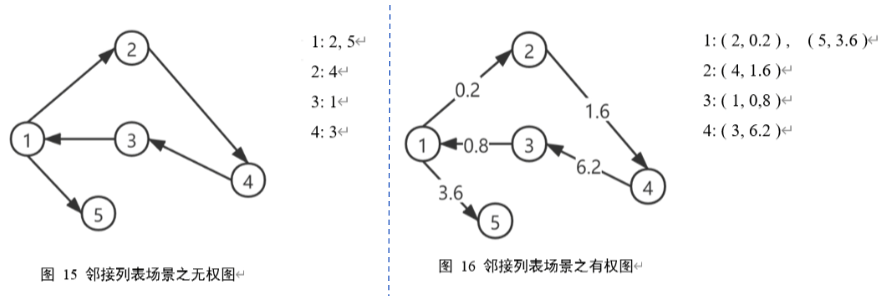
1.3.3 【例】边集
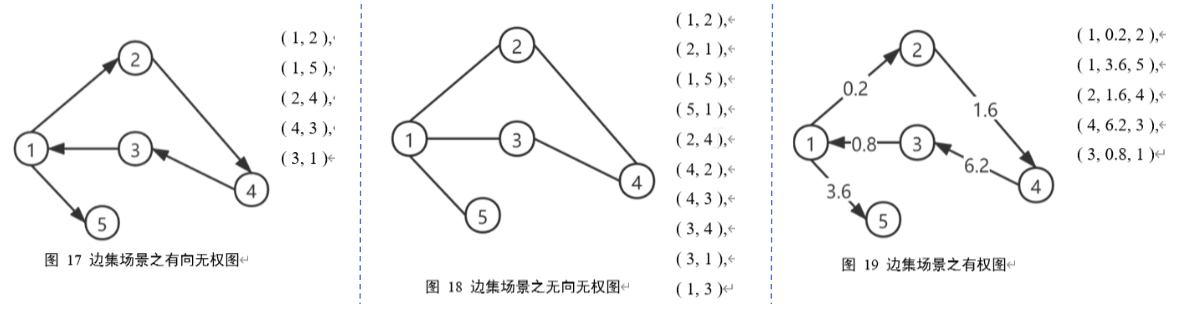
1.4 邻居、度
邻居(Neighbor):对于一个节点 v,它的邻居就是所有与它直接相连的节点。
度(Degree):一个节点的度就是它有多少个邻居,即与它相连的边的数量。
1.5 结构特征、节点特征、边特征
节点特征告诉你"我是谁";
边特征告诉你"我们关系如何";
结构特征告诉你"我在图里处于什么位置"