1 机器学习概念
机器学习是一种通过算法和模型使计算机从数据中自动学习并进行预测或决策的技术,属于人工智能的一个分支。其核心目标是让计算机在没有明确编程指令的情况下,通过对大量数据的分析,识别模式和规律,从而构建适应新数据的模型。机器学习包括监督学习、无监督学习和强化学习等不同类型,广泛应用于图像识别、自然语言处理、推荐系统和自动驾驶等领域,具备自适应、自动化和泛化能力,是数据驱动的技术创新。
领域内的一些学者也对机器学习给出了定义------
汤姆·米切尔(Tom Mitchell)是卡内基梅隆大学的计算机科学教授,被认为是机器学习领域的奠基人之一。他的经典定义在机器学习教科书中被广泛引用:
如果计算机程序在完成某类任务T时,通过经验E在某一表现度量P下的表现有所提高,则称该程序从经验E中学习。
机器学习的目标是使用计算机预测未知的事件或场景。1959年,亚瑟·塞缪尔(Arthur Samuel)将机器学习描述为"赋予计算机在没有明确编程指令下学习能力的研究领域"。他断言,编程计算机通过经验进行学习,最终应能消除大部分详细编程工作的需求 [1]。
1.1 机器学习算法
-
监督学习
监督学习(Supervised Learning)是机器学习中最常见的学习方式之一。监督学习通过对已有标记数据进行学习,训练模型能够从未标记数据中进行预测和分类。在监督学习中,每个样本都有标签(标记),模型可以利用这些标签来学习分类模型。
例如,一个模型需要识别手写数字,监督学习算法可以使用大量已经被标记好的手写数字图像作为训练集,每个图像都有一个标记,指明它是哪个数字。然后,该算法会自动从训练集中学习到数字之间的差异,使得在未知图像上也能够准确地识别数字。
监督学习应用广泛,可以应用于图像识别、自然语言处理、语音识别、推荐系统等领域。
优点:可以通过大量已有标记数据训练模型,使得模型的预测结果更加准确。
可以对数据进行分类和预测。
缺点:需要大量的已标记数据,而且需要人工进行标记。
模型只能预测已知类别,对于未知类别的数据无法进行有效预测。
- 分类算法
- 逻辑回归
- 决策树
- 随机森林
- 支持向量机
- 朴素贝叶斯
- K近邻
- 神经网络
- 回归算法
- 线性回归
- 多项式回归
- 支持向量回归
- 分类算法
-
无监督学习
无监督学习(Unsupervised Learning)是一种机器学习技术,用于处理未标记的数据,即没有给定输出标签的数据。无监督学习的目标是学习数据中的模式和结构,以便在未知数据上进行分类和预测。
例如,在无监督学习中,模型可以使用聚类算法对数据进行分组,每个组内的数据具有相似的特征。这种方法可以用于分析消费者行为模式、分析天文数据、分析文本数据等。
优点:无需标记大量数据,降低了数据标记的成本。
可以自动发现数据的结构和模式,可以帮助解决一些特定问题,如异常检测、聚类分析等。
缺点:无法利用标记数据进行训练,因此预测结果可能不够准确。
很难对生成的结果进行验证和解释,需要人工进行进一步分析。
- 聚类算法
- K均值
- 层次聚类
- DBSCAN
- 高斯混合模型
- 降维算法
- 主成分分析PCA
- t-SNE
- 自编码器
- 关联规则
- 聚类算法
-
强化学习
强化学习(Reinforcement Learning)是一种机器学习技术,用于培养智能体(Agent)通过与环境的交互来学习最佳决策策略。强化学习的目标是使智能体获得最大的累积奖励,从而学会在特定环境下做出最佳决策。
例如,在强化学习中,可以使用Q-learning算法训练一个智能体来玩某个游戏。该智能体需要不断地与游戏环境交互,学习最佳策略,使游戏得分最高。
优点:
可以处理与环境交互的问题,如机器人导航、自动驾驶等。
可以学习最佳策略,使得智能体在特定环境下做出最优决策。
缺点:训练时间较长,需要进行大量的试验和训练。
需要精心设计奖励函数,使得智能体能够学习到最佳策略。
-
半监督学习
半监督学习(Semi-supervised Learning)是介于监督学习和无监督学习之间的一种学习方式。半监督学习利用一小部分已标记数据和大量未标记数据进行训练,以提高模型的预测能力。
例如,在半监督学习中,可以使用少量已标记数据来训练模型,然后使用未标记数据来进一步完善模型。这种方法可以用于文本分类、图像识别等任务。
优点:
可以减少标记数据的数量,降低数据标记的成本。
可以利用未标记数据来提高模型的预测能力,使预测结果更加准确。
缺点:需要大量未标记数据,模型可能会过度拟合未标记数据,导致预测结果不准确。
无法处理未知类别的数据。
2 机器学习算法介绍
2.1 线性回归
2.1.1 核心思想
找到一个线性模型(一条直线或一个超平面),使得它能够最好地拟合一组数据点。
"线性":指的是模型是输入特征(x)的线性组合。
"回归":意味着我们要预测的是一个连续的数值(如房价、温度、销售额),而不是一个类别。
2.1.2 基本模型
模型方程: y = w₁x₁ + w₂ x₂ + ... + wₙ*xₙ + b
y:要预测的目标值。
x₁, x₂, ..., xₙ:n 个不同的特征。
w₁, w₂, ..., wₙ:每个特征对应的权重。
b:偏置项。
为了书写方便,我们通常用向量形式表示:
Y = WᵀX + b
其中 W 和 X 都是向量。
2.1.3 损失函数
均方误差:计算所有预测值与真实值之间差距的平方和,再求平均值。

2.1.4 模型评估
-
均方误差(MSE):就是我们的损失函数本身。值越小越好。
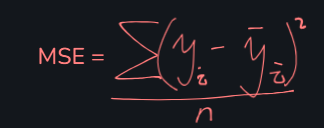
-
均方根误差(RMSE):与 MSE含义相同

-
平均绝对值误差(MAE): 与 MSE含义相同,对异常值不如MSE敏感
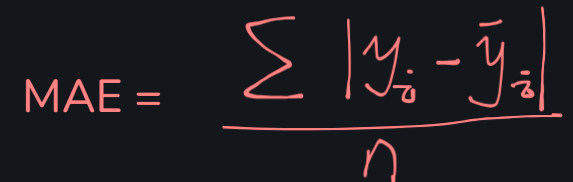
-
R² 决定系数:表示模型能够解释的目标变量方差的比例。值越接近 1,说明模型拟合得越好。

具体详见:深度解析决定系数
-
特征之间相关性:
-
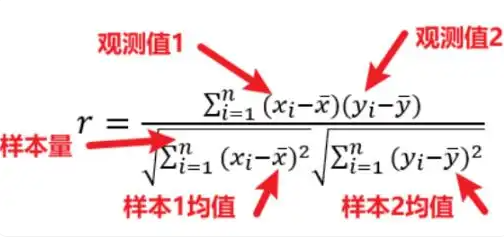
Pearson
pearson 法则是一种经典的相关系数计算方法,主要用于表征线性相关性,假设2个变量服 从正态分布且标准差不为0,他的值介于-1到1之间,pearson相关系数的绝对值越接近于1,表明 2个变量的相关程度越高,即这2个变量越相似。
-
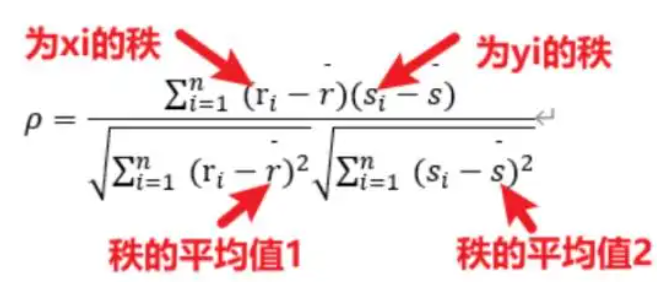
Spearman
pearman 相关性分析是对两组变量的等级大小作相关性分析,从而得到一个自变量与因变量之间的关系和自变量对因变量的影响强弱。它首先将两组变量的数据按照大小顺序排列,然后用等级代替原始数据,最后计算等级之间的相关性。
-
Kendall等级相关
kendall相关系数也叫kendall秩相关系数,广泛用于量化不同变量间的相关程度,作为一类无参数假设检验,用于衡量两变量之间的相关性,其并不要求数据满足正态分布,对于样本容量也没有过多要求,适用性比较广。
关于
-
2.1.5 特征值W的求解方法
2.1.5.1 线性回归一般流程
- 数据处理/分析
- 异常数据的处理
- 通过散点图,折线图,热力图(相关性矩阵),条形图等分析不同维度特性之间的关系,便于选取合适的算法进行训练
- 数据的归一化或者标准化处理
数据是否需要进行标准化处理是跟不同维度数据的差异及训练模型有关,一般,对于随机梯度下降回归及分类算法都需要对数据进行标准化处理。防止不同维度的数据差异过大,影响训练结果。
详见:
为什么要做特征归一化/标准化?
史上最全|特征标准化的效果分析与应用场景(有干货,含实操)
- 线性回归算法与损失函数的选择
详见:
损失函数(Loss Function)详细介绍 - 正则化
详见:
正则化技术详解:L1、L2正则的数学原理与实现
史上最全|特征标准化的效果分析与应用场景(有干货,含实操) - 模型能力评估
通过均差,均方差与R2系数确认当前模型拟合能力
2.1.5.2 最小二乘法
W = (XᵀX)⁻¹Xᵀy
其中X:特征矩阵,每一行是一个样本,每一列是一个特征;Y:包含所有目标值的向量。
推导过程详见:最小二乘法推导及求解
优点:
不需要选择学习率。
当特征数量 n 不大时,计算非常快。直接得到精确解。
缺点:
当特征数量 n 非常大时(例如 >10,000),计算逆矩阵 (XᵀX)⁻¹ 的代价非常高,速度很慢。
只能用于线性模型,不适用于更复杂的模型。
代码案例:
- 数据集:linear_regression_dataset
- 代码实现
kaggle
2.1.5.3 梯度下降法
关于梯度下降法的原理详见:
梯度下降法
机器学习损失函数中的正则化Regularization化快速明晰
常见学习率衰减方式
机器学习中的学习率及其衰减方法全面解析
关于梯度下降法的代码实现及应用详见:
梯度下降求解线性回归问题