1.顺序表特点与基本操作
1.1 顺序表定义
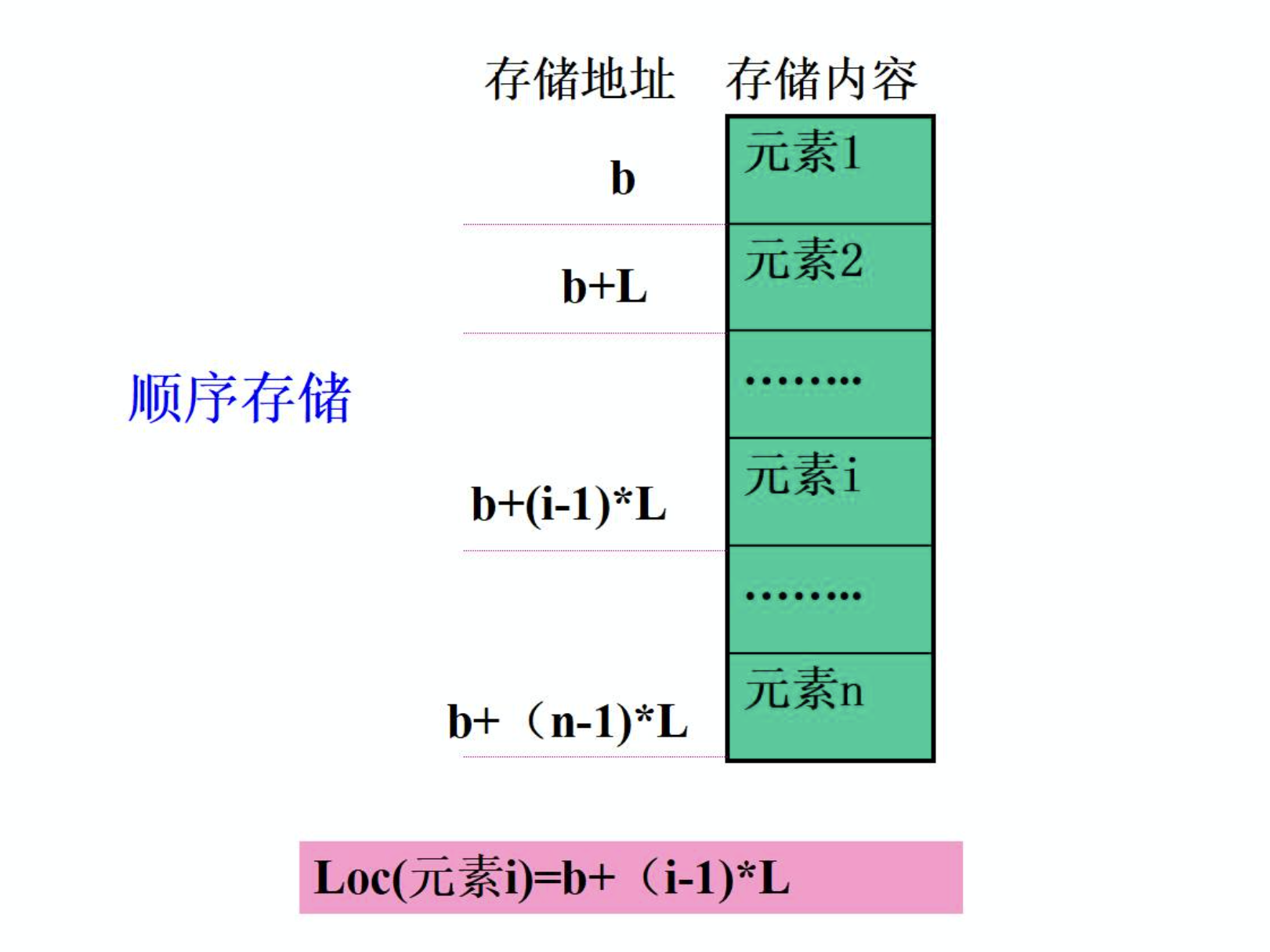
顺序表是一种线性表的存储结构,采用连续的内存空间存储数据元素。其逻辑顺序与物理顺序一致,通过数组实现,支持随机访问。顺序表属于静态存储结构,但可通过动态分配内存实现扩容。
1.2 顺序表特点
内存连续
所有元素存储在地址连续的存储单元中,通过首地址和下标可直接计算出元素位置,访问时间复杂度为 O(1)。
预先分配空间
需提前定义最大容量,静态分配可能导致空间浪费或不足。动态分配虽可扩容,但需重新申请内存并迁移数据,时间复杂度为O(n)。
插入删除效率低
在非尾部位置操作时,需移动后续元素以保持连续性。平均时间复杂度为 O(n),尾部操作则为 O(1)。
1.3 顺序表类型定义
cs
// 定义顺序表结构体
typedef struct {
int *elem; // 指向存储元素的动态数组基地址
int length; // 当前顺序表中元素的实际个数
int listsize; // 当前顺序表分配的存储空间大小(最大能容纳的元素个数)
} sqlist;1.4 初始化顺序表
cs
/**
* 初始化顺序表
* @param L 待初始化的顺序表(引用传递,修改会影响实参)
* @param n 初始要存入的元素个数
* @return 1-初始化成功;0-内存分配失败
*/
int init(sqlist &L,int n) {
// 为顺序表分配能存储100个int元素的初始空间
L.elem = (int*)malloc(100 * sizeof(int));
if (!L.elem) { // 内存分配失败(返回NULL)
return 0;
}
L.length = 0; // 初始元素个数为0
// 循环读取n个元素存入顺序表
for (int i = 0; i < n; i++) {
scanf("%d", &(L.elem[i])); // 读取元素到数组对应位置
L.length++; // 每存入一个元素,实际长度加1
}
L.listsize = 100; // 记录当前分配的最大容量
return 1; 1.5 插入操作
cs
/**
* 向顺序表中插入元素
* @param L 目标顺序表(引用传递)
* @param i 插入位置(逻辑位置,从1开始计数)
* @param e 要插入的元素值
* @return 1-插入成功;0-位置不合法或内存扩容失败
*/
int insert(sqlist &L, int i, int e) {
int *newspace; // 用于扩容时指向新的内存空间
int *p; // 指向需要移动的元素
int *q; // 指向插入位置
// 检查插入位置合法性:必须在1到当前长度+1之间(允许插在表尾)
if (i < 1 || i > L.length + 1) {
return 0;
}
// 若当前元素个数已达最大容量,需要扩容
if (L.length >= L.listsize) {
// 重新分配内存:在原有大小基础上增加10个元素的空间
newspace = (int*)realloc(L.elem, (L.listsize + 10) * sizeof(int));
if (!newspace) { // 扩容失败
return 0;
}
L.elem = newspace; // 指向新的内存空间
L.listsize += 10; // 更新最大容量
}
q = &(L.elem[i - 1]); // 计算插入的物理位置(逻辑位置i对应数组下标i-1)
// 从最后一个元素开始,到插入位置为止,依次向后移动一个位置
// (避免覆盖后续元素,必须从后往前移)
for (p = &(L.elem[L.length - 1]); p >= q; --p) {
*(p + 1) = *p; // 后移元素
}
*q = e; // 在插入位置存入新元素
++L.length; // 实际长度加1
return 1; // 插入成功
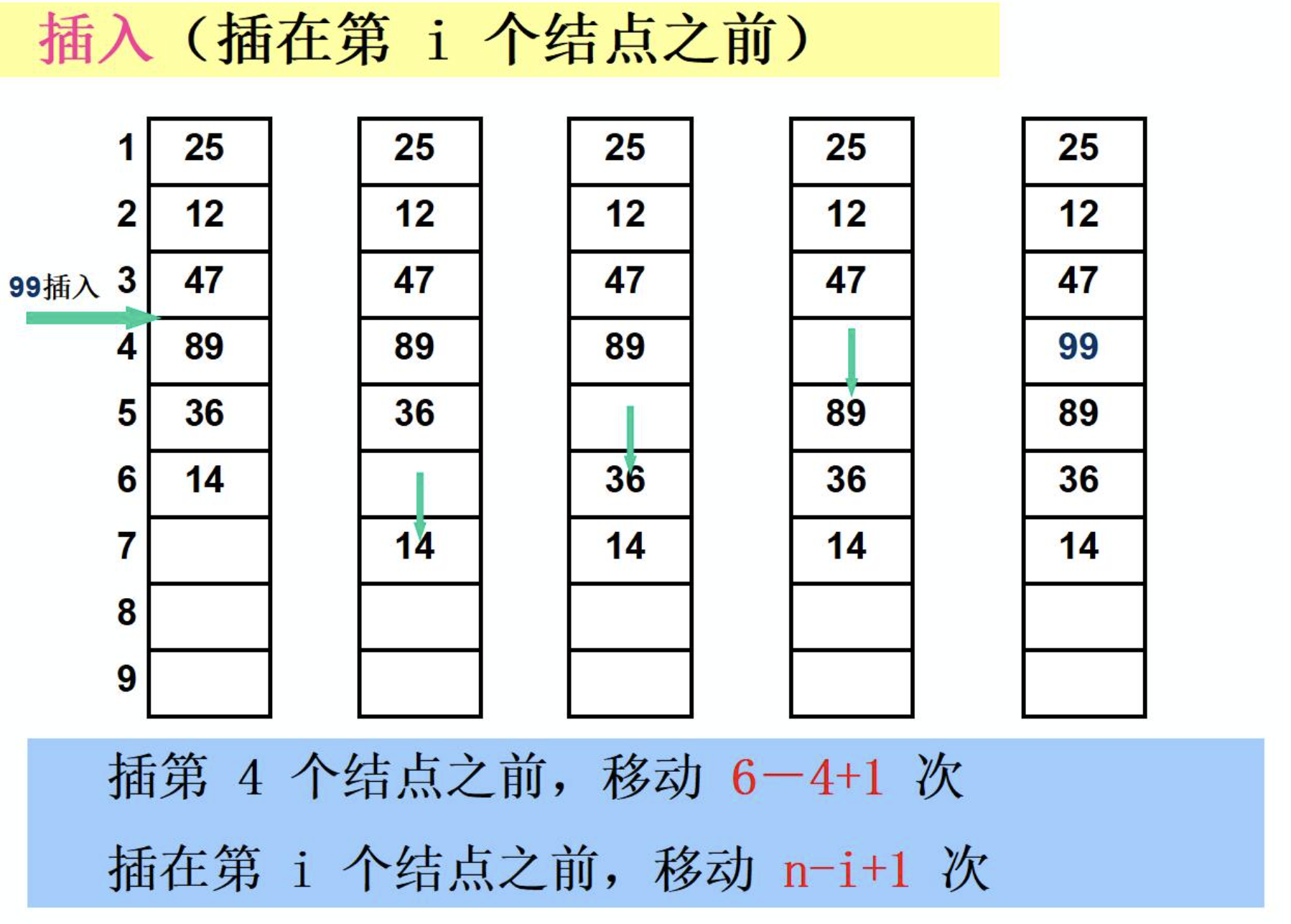
}图像解释与平均移动次数
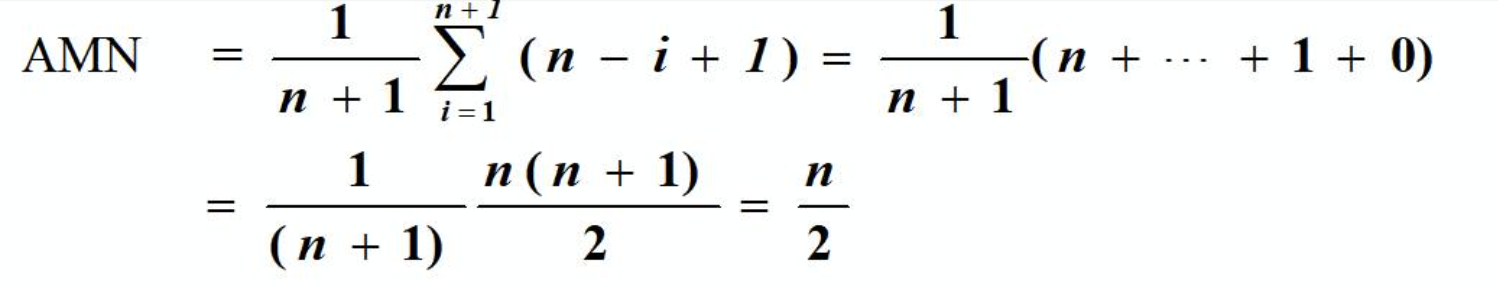
1.6 删除操作
cs
/**
* 从顺序表中删除元素
* @param L 目标顺序表(引用传递)
* @param i 要删除的元素位置(逻辑位置,从1开始计数)
* @param e 用于保存被删除的元素值(输出参数)
* @return 1-删除成功;0-位置不合法
*/
int dele(sqlist &L, int i, int &e) {
int *q; // 指向顺序表最后一个元素
int *p; // 指向要删除的元素
// 检查删除位置合法性:必须在1到当前长度之间
if (i < 1 || i > L.length) {
return 0;
}
p = &(L.elem[i - 1]); // 找到要删除元素的物理位置(下标i-1)
e = *p; // 保存被删除的元素值
q = L.elem + L.length - 1; // 指向最后一个元素(下标length-1)
// 从删除位置的下一个元素开始,到最后一个元素为止,依次向前移动一个位置
for (++p; p <= q; ++p) {
*(p - 1) = *p; // 前移元素,覆盖被删除的位置
}
--L.length; // 实际长度减1
return 1; // 删除成功
}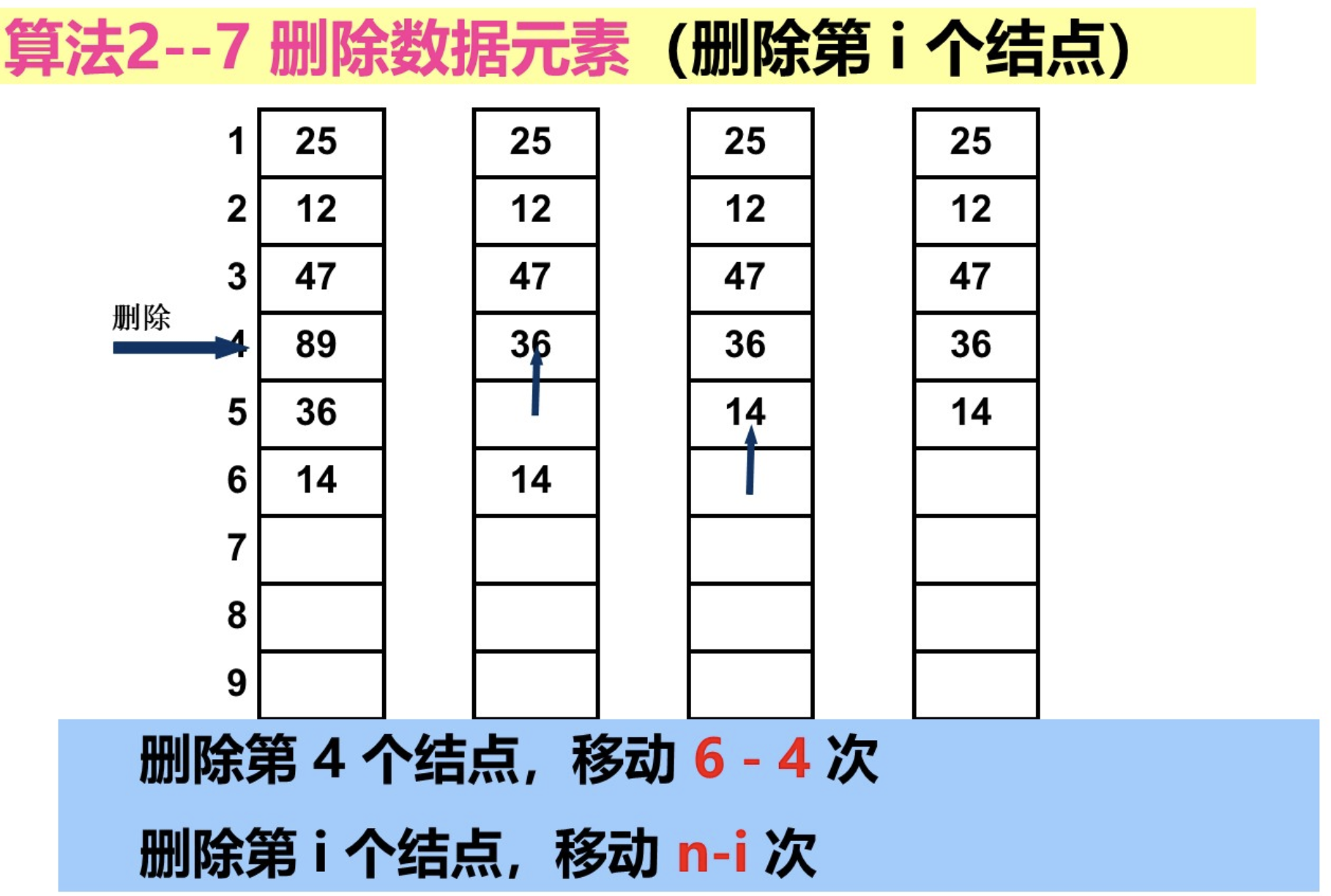
算法时间主要花费在移动元素上
若删除尾节点,则根本无需移动,特别快。
若删除首节点,n-1个元素全部需要前移,特别慢。
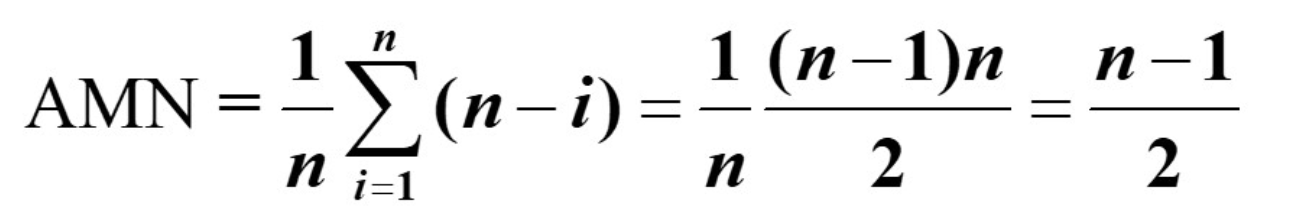
1.7 查找元素位置
输入元素值,返回该元素值的位置
cs
/**
* 查找顺序表中指定元素的位置
* @param L 目标顺序表(值传递,不修改原表)
* @param e 要查找的元素值
* @return 元素的逻辑位置(从1开始);0-未找到
*/
int locate(sqlist L, int e) {
int i = 1; // 记录逻辑位置(初始为第一个元素)
int *p = L.elem; // 指向第一个元素的指针
// 循环遍历元素:未超出长度且未找到目标时继续
while ((i <= L.length) && (*p != e)) {
i++; // 位置后移
p++; // 指针后移(指向下一个元素)
}
// 若找到(i未超出长度),返回逻辑位置;否则返回0
if (i <= L.length) {
return i;
} else {
return 0;
}
}1.8 遍历打印顺序表
cs
void display(sqlist L) {
for (int i = 0; i < L.length; i++) {
printf("%d ", L.elem[i]);
}
printf("\n"); 1.9 完整代码
cs
#include<stdio.h>
#include<stdlib.h>
typedef struct {
int *elem;
int length;
int listsize;
} sqlist;
// 初始化顺序表
int init(sqlist &L,int n) {
L.elem=(int*)malloc(100*sizeof(int));
if(!L.elem) return 0; // 内存分配失败
L.length=0;
for(int i=0; i<n; i++) {
scanf("%d",&(L.elem[i]));
L.length++;
}
L.listsize=100;
return 1;
}
// 插入元素
int insert(sqlist &L,int i,int e) {
int *newspace;
int *p;
int *q;
if(i<1||i>L.length+1) return 0; // 位置不合法
if(L.length>=L.listsize) { // 需要扩容
newspace=(int*)realloc(L.elem,(L.listsize+10)*sizeof(int));
if(!newspace) return 0; // 扩容失败
L.elem=newspace;
L.listsize+=10;
}
q=&(L.elem[i-1]); // 插入位置
// 从后往前移动元素
for(p=&(L.elem[L.length-1]); p>=q; --p) {
*(p+1)=*p;
}
*q=e; // 插入新元素
++L.length;
return 1;
}
// 删除元素
int dele(sqlist &L,int i,int &e) {
int *q;
int *p;
if(i<1||i>L.length) return 0; // 位置不合法
p=&(L.elem[i-1]);
e=*p; // 保存要删除的元素
q=L.elem+L.length-1; // 最后一个元素位置
// 从删除位置往后移动元素
for(++p; p<=q; ++p) *(p-1)=*p;
--L.length;
return 1;
}
// 查找元素
int locate(sqlist L,int e) {
int i=1;
int *p=L.elem;
while((i<=L.length)&&(*p!=e)) {
i++;
p++;
};
if(i<=L.length) return i; // 找到返回位置
else return 0; // 未找到返回0
}
// 显示链表内容
void display(sqlist L) {
for(int i=0; i<L.length; i++)
printf("%d ",L.elem[i]);
printf("\n");
}
int main() {
sqlist p;
int i,e,n;
int s; // 操作选择
printf("输入建立顺序表大小n:\n");
scanf("%d",&n);
printf("输入顺序表的值(空格分隔):\n");
if(!init(p,n)) { // 检查初始化是否成功
printf("初始化失败!\n");
return 1;
}
printf("建立的顺序表表为:\n");
display(p);
do {
printf("\n请选择操作:\n");
printf("1. 插入元素\n");
printf("2. 删除元素\n");
printf("3. 查找元素\n");
printf("0. 退出程序\n");
scanf("%d",&s); // 修正:添加取地址符&
switch(s) {
case 1:
printf("请输入插入位置和元素值(用空格分隔):\n");
scanf("%d%d",&i,&e);
if(insert(p,i,e)) {
printf("插入成功!当前链表为:\n");
display(p);
} else {
printf("插入失败!位置不合法或内存不足\n");
}
break;
case 2:
printf("请输入要删除的位置:\n");
scanf("%d",&i);
if(dele(p,i,e)) {
printf("删除成功!删除的元素是:%d\n",e);
printf("当前链表为:\n");
display(p);
} else {
printf("删除失败!位置不合法\n");
}
break;
case 3:
printf("请输入要查找的元素值:\n");
scanf("%d",&e);
i = locate(p,e);
if(i!=0) {
printf("元素%d的位置是:%d\n",e,i);
} else {
printf("未找到元素%d\n",e);
}
printf("当前链表为:\n");
display(p);
break;
case 0:
printf("操作结束,退出程序\n");
break;
default:
printf("输入错误,请重新选择\n");
}
} while(s!=0);
// 释放动态分配的内存
free(p.elem);
return 0;
}1.10 顺序表的优缺点
顺序表优点
存储密度大,存储效率高
顺序表采用连续的内存空间存储数据,无需额外的指针或链接信息,存储密度接近100%,空间利用率高。
随机访问快速
通过下标可在 O(1) 时间内直接访问任意元素,适合频繁查询或需要快速定位的场景。
顺序表缺点
插入,删除效率低
在非尾部位置插入或删除元素时,需要移动大量元素以保证连续性,时间复杂度为 O(n)。
固定容量限制
静态存储形式,元素个数不能自由扩充。静态分配内存的顺序表需预先指定最大容量,可能导致空间浪费或溢出;动态分配虽可扩容,但需复制全部数据,开销较大。
2.链表特点与基本操作
2.1 链表的定义
链表是一种线性数据结构,由一系列节点(Node)组成,每个节点包含两部分:
- 数据域:存储实际的数据。
- 指针域 :存储指向下一个节点的地址(或引用)。
链表通过指针将节点按逻辑顺序连接,形成链式结构。
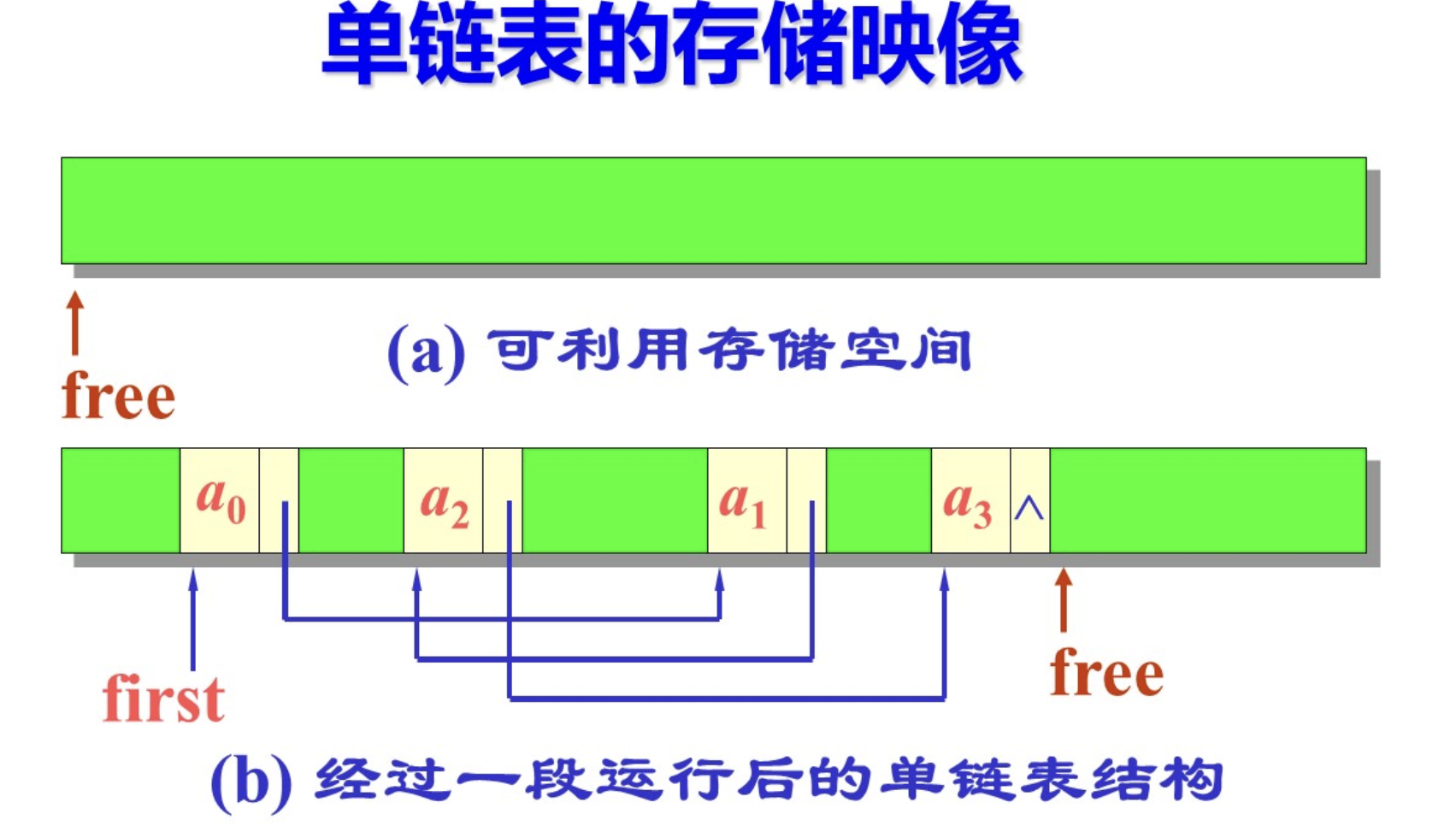
2.2 链表的特点
动态内存分配
- 链表的节点在内存中不必连续存储,通过指针动态关联,因此长度可灵活调整。
插入与删除高效
- 时间复杂度为 O(1)(若已知操作位置的前驱节点)。
- 无需像数组那样移动大量元素。
随机访问效率低
- 需从头节点开始遍历,时间复杂度为 O(n)。
链式存储结构
- 节点在存储器上的位置是任意的,逻辑上相邻的元素在物理上不一定会相邻。
- 节点内部存储空间不连续,节点之间存储空间连续。
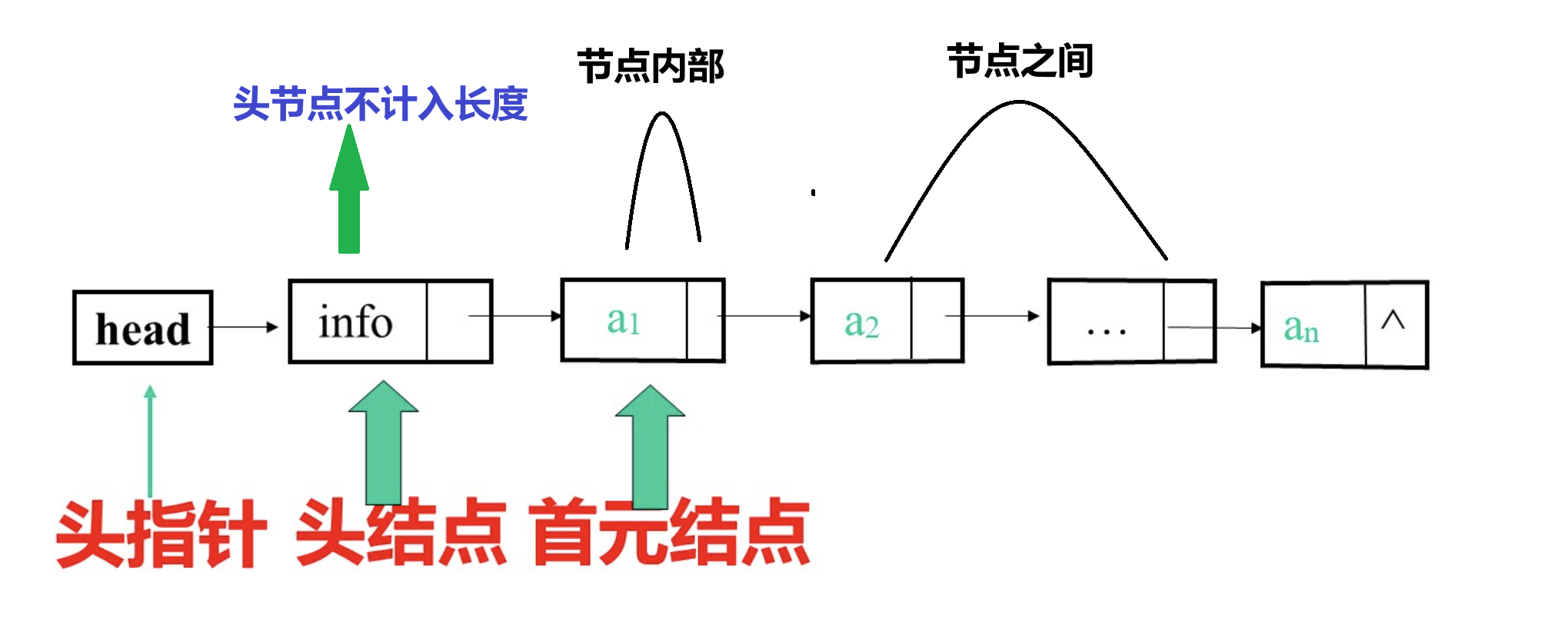

2.3单链表的定义与表示
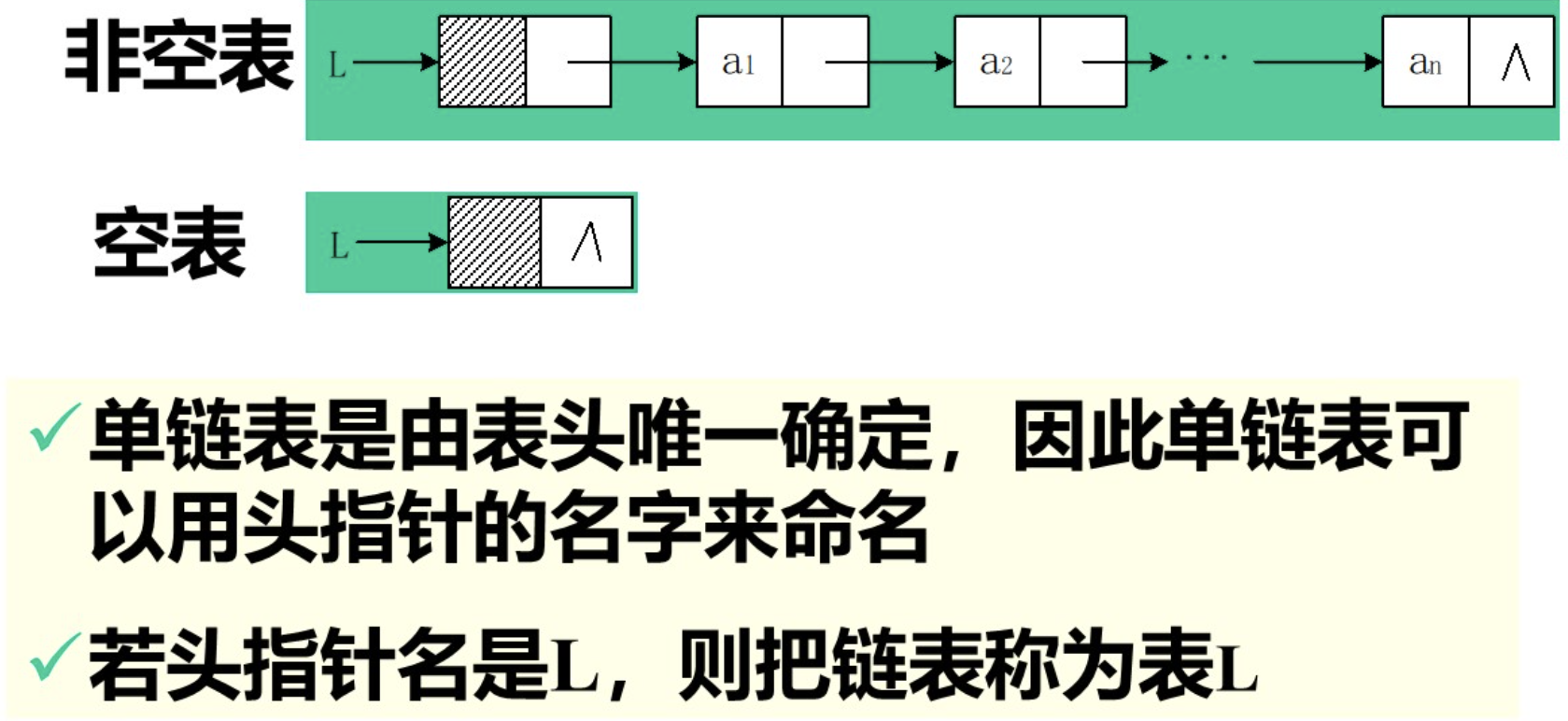
cs
// 定义单链表节点结构体
typedef struct lnode{
int data; // 节点存储的数据
struct lnode *next; // 指向后继节点的指针
}lnode, *link; // lnode为节点类型,link为节点指针类型(指向lnode的指针)2.4 创建链表
2.4.1 逆序创建(头插法)
cs
/**
* 逆序创建单链表(头插法)
* 功能:输入n个元素,按逆序插入到链表中(新元素始终插在头节点之后)
* @param L 链表头指针的引用(通过引用修改实参的头指针)
* @param n 要创建的链表节点个数
* @return 1-创建成功
*/
int f_creat(link &L,int n){
int i;
struct lnode *p; // 临时指针,用于指向新创建的节点
// 创建头节点
L=(link)malloc(sizeof(lnode));
L->next=NULL; // 头节点初始后继为NULL(空链表状态)
// 循环创建n个节点
for(int i=0;i<n;i++){
p=(link)malloc(sizeof(lnode)); // 为新节点分配内存
scanf("%d",&p->data);
// 头插法核心:新节点的后继指向当前头节点的后继
p->next=L->next;
// 头节点的后继指向新节点(将新节点插入到头节点之后)
L->next=p;
}
return 1; // 创建成功
} 2.4.2 正序创建(尾插法)
cs
/**
* 正序创建单链表(尾插法)
* 功能:输入n个元素,按输入顺序依次插入到链表尾部,最终链表顺序与输入顺序一致
* @param L 链表头指针的引用(用于修改外部头指针)
* @param n 要创建的节点个数
* @return 1-创建成功
*/
int t_creat(link &L, int n) {
// 1. 创建头节点
L = (link)malloc(sizeof(lnode));
L->next = NULL; // 头节点初始后继为NULL(空链表状态)
// 2. 定义尾指针p,初始指向头节点(此时头节点是链表的最后一个节点)
link p = L;
// 3. 循环创建n个节点,并按顺序插入到链表尾部
for (int i = 0; i < n; i++) {
// 创建新节点s
link s = (link)malloc(sizeof(lnode));
scanf("%d", &s->data);
// 将新节点s链接到当前尾节点p的后面
p->next = s;
// 尾指针p移动到新节点s(更新尾节点为s)
p = s;
}
// 4. 链表创建完成后,将最后一个节点的后继置为NULL(标记链表结束)
p->next = NULL;
return 1;
}2.5 获取元素
cs
/**
* 获取链表中第i个元素的值
* @param L 链表头指针(头节点)
* @param i 要获取的元素位置(逻辑位置,从1开始计数)
* @param e 用于存储获取到的元素值(输出参数)
* @return 1-获取成功;0-位置不合法(i超出范围)
*/
int get(link L,int i ,int &e){
link p; // 遍历指针,用于指向当前节点
p=L->next; // 从第一个数据节点(头节点的后继)开始遍历
int j=1; // 记录当前遍历到的位置(初始为第一个节点)
// 循环找到第i个节点:p不为空且未到达第i个节点时继续后移
while(p && j<i){
p=p->next; // 指针后移,指向下一个节点
j++;
}
if(!p || j>i) return 0;
e=p->data; // 找到第i个节点,将数据存入e
return 1; // 获取成功
}2.6 插入元素
在第i个位置插入元素e,要先找到第i-1个位置
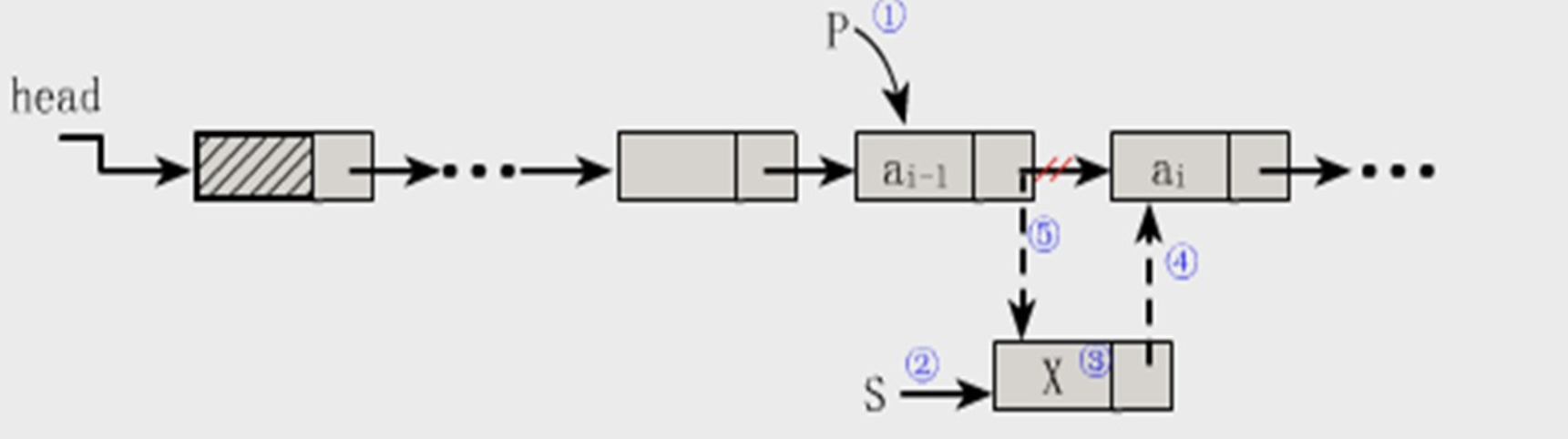
核心步骤:
cs
s->next=p->next;
p->next=s; 上述两行代码不能交换位置
cs
/**
* 在链表第i个位置插入元素e
* @param L 链表头指针(头节点)
* @param i 插入位置(逻辑位置,从1开始,可插在表尾)
* @param e 要插入的元素值
* @return 1-插入成功;0-位置不合法
*/
int insert(link L,int i,int e){
struct lnode *s; // 指向新创建的插入节点
struct lnode *p; // 遍历指针,用于找到第i-1个节点(插入位置的前驱)
int j=0; // 记录当前位置(初始为头节点,位置0)
p=L; // 从头部点开始遍历
// 找到第i-1个节点:p不为空且未到达目标位置时继续后移
while(p && j<i-1){
p=p->next; // 指针后移
j++; // 位置计数加1
}
if(!p || j>i-1) return 0;
// 创建新节点并赋值
s=(link)malloc(sizeof(lnode));
s->data=e;
// 插入核心操作:先连后,再连前(避免断链)
s->next=p->next; // 新节点的后继指向p的原后继
p->next=s; // p的后继指向新节点
return 1; /
}2.7 删除节点
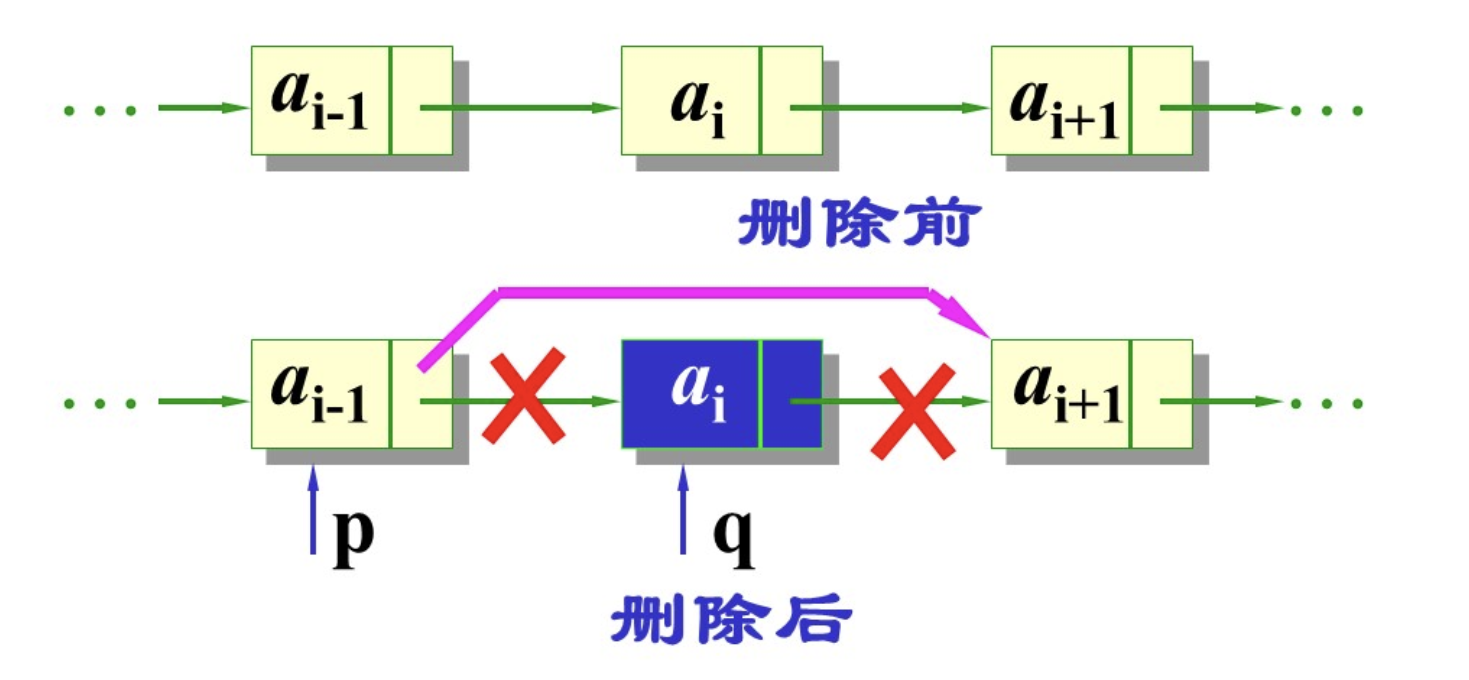
核心步骤:
cs
p->next=p->next->next用q记录删除的节点,以便于释放内存
cs
/**
* 删除链表中第i个元素
* @param L 链表头指针的引用
* @param i 要删除的元素位置(逻辑位置,从1开始)
* @param e 用于存储被删除的元素值(输出参数)
* @return 1-删除成功;0-位置不合法
*/
int del(link &L,int i,int &e){
struct lnode *p; // 遍历指针,用于找到第i-1个节点(删除位置的前驱)
p=L; // 从头部点开始遍历
struct lnode *q; // 指向要删除的节点
int j=0; // 记录当前位置(初始为头节点,位置0)
// 找到第i-1个节点:p的后继不为空(确保有第i个节点)且未到达目标位置
while(p->next && j<i-1){
p=p->next;
j++;
}
// 若p的后继为空(i超过链表长度)或j>i-1(i小于1),则位置不合法
if(!p->next || j>i-1) return 0;
q=p->next; // q指向要删除的第i个节点
p->next=q->next; // 将p的后继指向q的后继(跳过q,实现删除)
e=q->data; // 保存被删除节点的数据
free(q); // 释放被删除节点的内存
return 1;
}2.8 遍历打印链表
cs
void see(link L){
struct lnode *p;
p=L;
while(p->next)
{
p=p->next;
printf("%d ",p->data);
}
}2.9 完整代码
cs
#include<stdio.h>
#include<stdlib.h>
typedef struct lnode{
int data;
struct lnode *next;
}lnode,*link;
//逆序创建链表
int f_creat(link &L,int n){
int i;
struct lnode *p;
L=(link)malloc(sizeof(lnode));
L->next=NULL;
for(int i=0;i<n;i++){
p=(link)malloc(sizeof(lnode));
scanf("%d",&p->data);
p->next=L->next;
L->next=p;
}
return 1;
}
//正序创建链表
int t_creat(link &L, int n) {
L = (link)malloc(sizeof(lnode));
L->next = NULL;
link p = L;
for (int i = 0; i < n; i++) {
link s = (link)malloc(sizeof(lnode));
scanf("%d", &s->data);
p->next = s;
p=s;
}
p->next=NULL;
return 1;
}
int get(link L,int i ,int &e){
link p;
p=L->next;
int j=1;
while(p && j<i){
p=p->next;
j++;
}
if(!p || j>i) return 0;
e=p->data;
return 1;
}
int insert(link L,int i,int e){
struct lnode *s;
struct lnode *p;
int j=0;
p=L;
while(p && j<i-1){
p=p->next;
j++;
}
if(!p || j>i-1) return 0;
s=(link)malloc(sizeof(lnode));
s->data=e;
s->next=p->next;
p->next=s;
return 1;
}
//删除第i个元素
int del(link &L,int i,int &e){
struct lnode *p;
p=L;
struct lnode *q;
int j=0;
//p为第i-1个元素
while(p->next && j<i-1){
p=p->next;
j++;
}
if(!p->next || j>i-1) return 0;
q=p->next;
p->next=q->next;
e=q->data;
free(q);
return 1;
}
void see(link L){
struct lnode *p;
p=L;
while(p->next)
{
p=p->next;
printf("%d ",p->data);
}
}
int main()
{
link p,L,s;
int data;
int i,n,e;
int select;
printf("输入链表长度:\n");
scanf("%d",&n);
printf("输入链表的值,空格分隔:\n");
t_creat(L,n);
see(L);
do{
printf("\n1:取出\n");
printf("2:插入\n");
printf("3:删除\n");
printf("0:结束!\n");
printf("请输入选择\n");
scanf("%d",&select);
switch(select)
{
case 1:
printf("输入元素的位置i:\n");
scanf("%d",&i);
get(L,i,e);
printf("取出的元素是:%d\n",e);
break;
case 2:
printf("输入插入元素的位置i和值e,空格分隔\n");
scanf("%d%d",&i,&e);
insert(L,i,e);
printf("插入后所有元素为:\n");
see(L);
break;
case 3:
printf("输入要删除的元素位次i:\n");
scanf("%d",&i);
del(L,i,e);
printf("删除后所有元素为:\n");
see(L);
break;
case 0:
printf("操作结束");
break;
default: printf("选择出错");
}
}while(select!=0);
p=L;
while(p != NULL){
link temp = p;
p = p->next;
free(temp);
}
return 0;
}2.10 链表的优缺点
链表的优点
动态大小
链表不需要预先分配固定大小的内存空间,可以根据实际需求动态调整大小,适合数据量变化频繁的场景。
高效插入和删除
在链表中插入或删除节点只需修改相邻节点的指针,时间复杂度为 O(1)(已知位置时)。相比之下,数组需要移动大量元素,时间复杂度为 O(n)。
内存利用率高
链表节点在内存中不必连续存储,可以充分利用零散的内存空间,避免数组因连续内存分配导致的碎片问题。
灵活的结构扩展
链表可以轻松扩展为双向链表、循环链表等变体,支持更复杂的操作(如反向遍历),而数组结构固定。
链表的缺点
存储密度小,随机访问效率低
链表不支持直接索引访问,查找第 i个元素需要从头节点开始遍历,时间复杂度为 O(n)。数组的随机访问时间为 O(1)。
额外内存开销
每个节点需存储指针(或引用),占用额外内存。例如,单链表每个节点比数组多一个指针的空间开销。