【文献阅读】Deep-learning-aided dismantling of interdependent networks

authors：

• Weiwei Gu,
• Chen Yang,
• Lei Li,
• Jinqiang Hou &
• Filippo Radicchi

publish：NMI volume 7, pages1266--1277 (2025)

原文link:

Deep-learning-aided dismantling of interdependent networks | Nature Machine Intelligence

这篇文章提出的神经网络框架名为 MultiDismantler ，它是一个基于深度强化学习的多层图神经网络框架 ，专门用于解决相互依赖的多层网络拆解问题

🧠 神经网络框架概述

MultiDismantler 主要由以下两个核心组件构成：

1. 编码器 ：Multiplex Graph Neural Network

   用于对多层网络进行表示学习，捕捉层内和层间的结构信息。包含：

   ① 节点级层间注意力机制：动态计算不同层之间节点的影响力权重。 （box1）

   ② 层内图卷积网络 ：聚合每层内邻居节点的信息。

2. 解码器 ：n-step Deep Q-Network

   基于编码器输出的节点嵌入和状态嵌入，计算每个节点的 Q 值（预期回报），指导节点拆除策略。包含：

   ① 层级注意力机制 ：融合不同层的 Q 值，得到全局节点重要性评分。

   ② MLP ：用于计算每层内节点的 Q 值。

box1 相互依赖的多层网络输入给MultiDismantler ，每层结构是输入了邻接矩阵，层间耦合是怎么输入的？

MGNN编码器中的节点级层间注意力机制 能够自动学习并量化多层网络的层间耦合

给了两张邻接矩阵给神经网络，并没有告诉他这两个网络是耦合或者有关联的，也没有告诉它耦合方式，他怎么计算层间注意力呢？

🧩 具体实现方式

1. 节点表示初始化

在编码器开始时，每个节点在每个层中都有一个初始特征向量。通常使用节点的归一化度作为特征：

• 对于节点v，在层1的特征：X_v¹ = degree_in_layer1(v) / max_degree_layer1

• 对于节点v，在层2的特征：X_v² = degree_in_layer2(v) / max_degree_layer2

注意：虽然特征不同，但这是同一个节点v在不同层中的表现！

2. 层内信息聚合

首先在每个层内独立进行图卷积，得到：

• h_v¹ = 节点v在层1的表示（基于层1的邻接关系）

• h_v² = 节点v在层2的表示（基于层2的邻接关系）

3. 层间注意力计算（关键步骤）

现在进入您困惑的部分。对于同一个节点v，模型计算：

注意力权重 = softmax( 相似度(h_v¹, h_v²) )

这里：

• h_v¹ 和 h_v² 是同一个节点v在不同层中的表示

• 相似度计算衡量的是："节点v在层1的状态"与"节点v在层2的状态"之间的关联强度

为什么这能工作？

因为如果两个层高度相关，那么同一个节点在两个层中的表示也会相似，注意力权重就会高。反之，如果两个层不相关，同一个节点在两个层中的行为可能完全不同，注意力权重就会低。

注意力权重是为了刻画级联效应，这里的"相关性"实际上是一个代理指标，用于预测潜在的级联风险。

---

🔁 输入与输出

✅ 输入：

多层网络结构：包括：

• 每层的邻接矩阵 A(ℓ)：N×N 矩阵

• 节点特征（节点的归一化度）：N×1 向量
  计算公式：对于节点v在层ℓ，其特征是：X_v^ℓ = degree_of_node_v_in_layer_ℓ / max_degree_in_layer_ℓ ，衡量节点在该层中的相对重要性：

  • 如果节点A在层1有10个连接，层1的最大度是20，则 X_A¹ = 10/20 = 0.5

  • 同一节点A在层2有5个连接，层2的最大度是10，则 X_A² = 5/10 = 0.5

• 层间耦合：架构设计（非显式输入）（box2）

box2

在文章的问题设定中（Methods部分有明确定义），他们处理的是"一对一相互依赖"的多层网络（也称为多重网络）。这意味着：

• 两个层（例如层1和层2）共享同一组节点集合V。

• 一个节点在不同层中有不同的连接关系（即不同的邻接矩阵 E(1)和 E(2)），但节点本身是同一个。

✅ 输出：

• 每个节点的 Q 值：表示在当前网络状态下拆除该节点所能获得的预期累积奖励。

• 节点拆除序列：根据 Q 值从高到低排序的节点拆除顺序，目标是高效瓦解网络的最大连通组件。

box 3

MultiDismantler的训练数据主要包括：

1. 训练阶段（小规模合成网络）

• 数据源 ：使用几何多层模型 生成的20,000+个合成多层网络 ( box 4)

• 网络规模：30-50个节点

• 网络结构 ：每个网络包含2个层，共享相同的节点集合

• 具体输入：

  • 层1的邻接矩阵

  • 层2的邻接矩阵

  • 没有显式的层间连接矩阵

2. 测试阶段（真实世界网络）

• 9个真实多层网络（如Sanremo2016、Homo、Fb&Fw等）

• 同样只提供各层的邻接矩阵，不提供层间连接信息

box 4

为什么不用经典的BA模型？

BA模型（Barabási-Albert Model） 是一个著名的单层网络生成模型。

• 优点：能生成符合现实世界"无标度"特性的网络（即少数节点拥有大量连接）。

• 致命缺点 ：它只能生成单个网络。如果你想用它创建一个双层的合成网络，你只能：

  1. 用BA模型独立生成网络A

  2. 再用BA模型独立生成网络B

  3. 然后随机地将两个网络中的节点配对，形成" interdependent "关系。

这样生成的训练数据有严重缺陷 ：它假设不同层之间的连接是随机的 ，层与层之间没有内在的、结构上的相关性。这不符合现实。

---

几何多重网络模型的优势

几何多重网络模型 则专门为生成多层网络而设计。它的核心思想是：

• 将每个节点映射到一个隐藏的几何空间（比如一个圆形）中的一个点上。

• 节点在每一层 中的连接概率，都取决于它们在这个共同的隐藏几何空间中的距离。

  • 在几何空间里靠得近的节点，在所有层中都有更高的概率相连。

  • 在几何空间里离得远的节点，在所有层中连接概率都较低。

这就引入了关键的"层间相关性"：

• 参数 g（层间相似性相关） ：这个模型有一个可调参数 g，它能精确控制两个网络层在结构上的相似程度。

  • g 值高：两个层的拓扑结构高度相似（即一个节点在一层中是枢纽，在另一层中大概率也是枢纽）。

  • g 值低：两个层的拓扑结构差异很大。

📊 文章中g参数的选择策略

1. 训练阶段：覆盖全范围

在生成训练数据 时，文章采用了广泛采样的策略：

• g的取值范围 ：[0, 1] 的连续区间

• 采样方式 ：在生成每个训练网络时，随机从该范围内选择一个g值

• 目的 ：让模型见识到各种可能的层间相关性，从而获得强大的泛化能力

具体实现（根据第2页描述）：

"我们调整一个参数同时保持其他两个参数不变来生成20个具有各种属性的互连网络...例如，为了在条件 g ∈ [0, 1], N = 1,024 下生成网络，我们设置 γ = 2.5 和 k = 6，并随机从0到1生成g值"

2. 测试阶段：系统变化g值

在评估性能 时，文章系统地变化g值来测试模型在不同相关性强度下的表现：

合成网络测试（图2a,b）：

• 固定其他参数（γ = 2.5, k = 6, N = 1,024）

• 系统地测试不同g值下的拆解性能

• 观察模型在整个g值谱系上的表现

消融实验（Supplementary Table 4c）：

文章专门在合成网络 上研究了训练时使用的g值范围对最终性能的影响：

• 训练了多个不同g值范围的agent

• 发现：在广泛g值范围上训练的模型性能最稳定

• 极端情况（只训练g=0或g=1）性能会下降

---

🛠️ 训练与学习方式

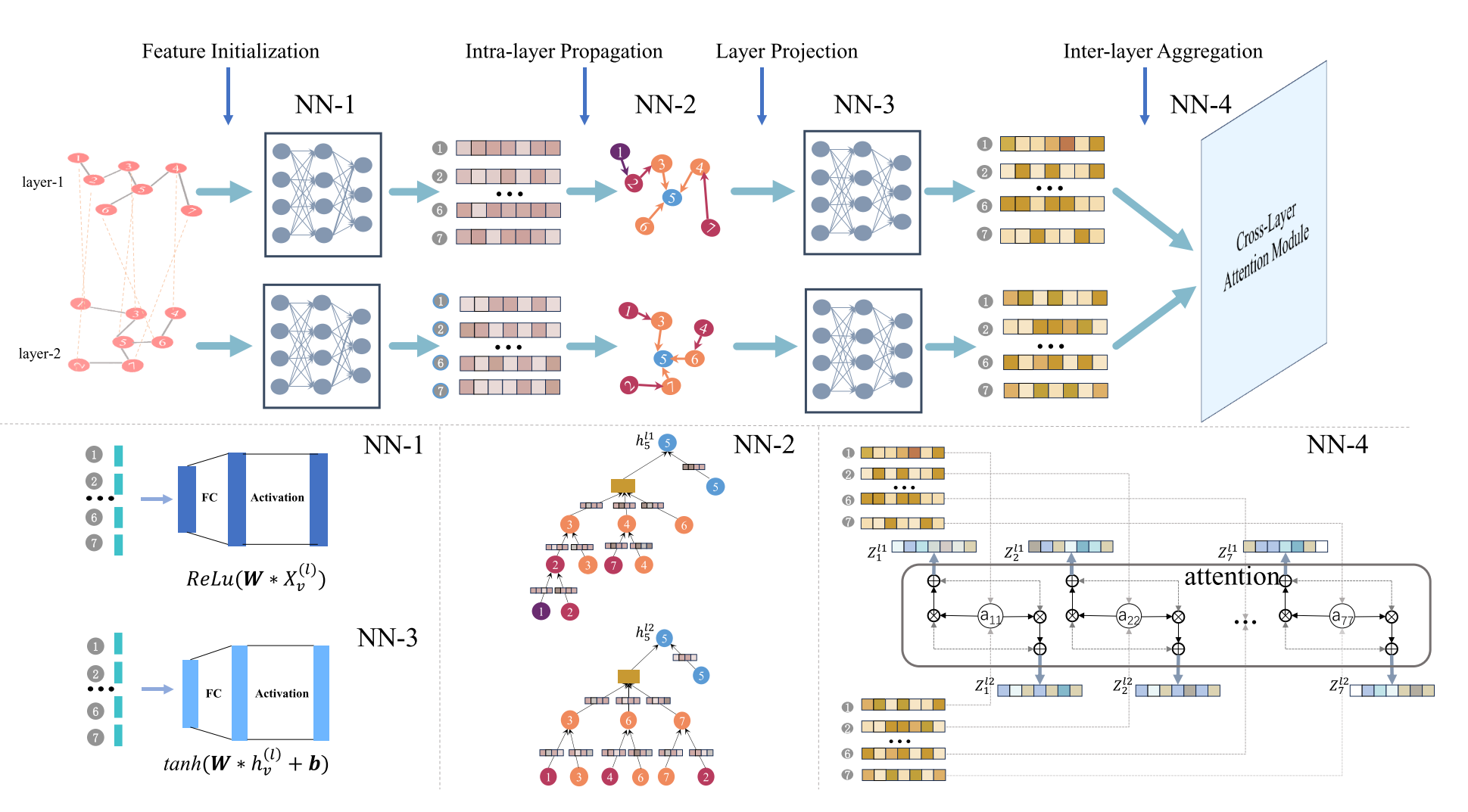
补充图5. MGNN的整体框架，包含特征初始化、层内消息传播、层投影和层间信息聚合四个模块。层内处理过程通过图卷积操作在各层级上根据节点局部邻域结构更新嵌入表示；层间处理过程利用注意力机制聚合不同层级的节点嵌入，使模型能够同时捕获层内与层间结构信息。

信息流动路径：

原始节点特征 → 初始嵌入 → [通过邻接矩阵传播] → 丰富的层内表示 → [跨层注意力] → 最终表示

模块1：特征初始化 → 公式5

python

# 公式5
h_v^{0(ℓ)} = Norm( ReLU( W₁ · X_v^ℓ ) )

信息流动：

• 输入 ：X_v^ℓ (原始节点特征，如归一化度)

• 处理：线性变换 + 激活函数 + 归一化

• 输出 ：h_v^{0(ℓ)} (初始节点嵌入)

• 作用：为图卷积准备良好的初始特征表示

---

模块2：层内消息传播 → 公式6

python

# 公式6
h_v^{k(ℓ)} = Norm( ReLU( W₄ · [ 
    (W₃ · h_v^{k-1(ℓ)})           # 自身信息
    ‖                             # 拼接
    (W₂ · ∑_{j∈N(v)^{(ℓ)}} h_j^{k-1(ℓ)})  # 邻居聚合
] ) )

信息流动：

• 输入 ：h_v^{k-1(ℓ)} (上一轮节点表示) + 邻接矩阵A(ℓ) (定义邻居)

• 处理：

  • 聚合所有邻居节点的表示

  • 与自身信息拼接

  • 通过神经网络变换

• 输出 ：h_v^{k(ℓ)} (更新后的节点表示)

• 作用 ：让节点了解自己在该层内的结构角色

---

模块3：层投影 → 公式7

python

# 公式7
h_v^{'(ℓ)} = tanh( W₅ · h_v^{(ℓ)} + b₁ )

信息流动：

• 输入 ：h_v^{(ℓ)} (层内传播后的最终表示)

• 处理：线性变换 + tanh激活

• 输出 ：h_v^{'(ℓ)} (投影后的节点表示)

• 作用 ：将不同层的表示映射到同一向量空间，使它们可以相互比较

---

模块4：层间信息聚合 → 公式8, 9

python

# 公式8：计算注意力权重
a_v^{(ℓ←q)} = softmax( W₆ · (h_v^{'(ℓ)} ⊙ h_v^{'(q)}) + b₂ )

# 公式9：跨层聚合
χ_v^{(ℓ)} = h_v^{'(ℓ)} + ∑_{q≠ℓ} a_v^{(ℓ←q)} · h_v^{'(q)}

信息流动：

• 输入 ：所有层的 h_v^{'(ℓ)} (投影后的表示)

• 处理：

  • 计算同一节点在不同层表示之间的相似度（Hadamard积）

  • 通过softmax得到归一化的注意力权重

  • 加权求和不同层的表示

• 输出 ：χ_v^{(ℓ)} (最终的节点表示，包含跨层信息)

• 作用：动态学习层间依赖强度，生成包含跨层信息的综合表示