卷积的直观理解

核心逻辑超直观：用 g 的 "形状" 去 "扫描" f，每移动一步就计算两者重叠部分的加权和，本质是动态的 "加权滑动平均" 。比如用平滑函数 g 卷积噪声信号 f，就像用滤网过滤杂质，得到更平稳的曲线；图像卷积里，3x3 的模糊核（g）扫过像素矩阵（f），每个像素都和周边像素加权融合，最终实现模糊 / 锐化效果。

个人理解，如果你还是无法通过上面的解释理解，可以试试我这个不太严谨的说法。两个函数相乘是f(t)*g(t)=h(t)，是在每一时刻t，将函数值相乘。卷积则是，每个时刻将一个函数的函数值相乘，然后按照时刻把这些函数叠加。

举个通俗的例子就是，函数1是一首音乐，函数2是一个逐渐衰减的函数。两者的乘积，是这首音乐声音逐渐变弱；两者的卷积，是这首音乐有逐渐衰减的回音或者跟唱。

再来个例子，你对着木桩打一拳，木桩会发生一个转动；再打一拳，再转动；你打极快的咏春拳，木桩各种动。那打一拳，木桩转动是一个函数；你如何打拳是另一个函数；你打拳使木桩动就是两个的卷积。

如果你还觉得不好理解请留言，或者你有更好的看法也可以留言。

程序帮助理解

以下用 MATLAB 实现 信号卷积 + 图像卷积 双案例，代码带详细注释，运行后能直观看到卷积效果：

一、信号卷积（平滑噪声信号）

Matlab 复制代码

% 1. 生成原始信号（含噪声的正弦波）
t = 0:0.01:2*pi;  % 时间轴（0到2π，步长0.01）
f = sin(t) + 0.3*randn(size(t));  % 原始信号：正弦波+高斯噪声（噪声幅度0.3）

% 2. 定义卷积核（平滑滤波器：5点移动平均）
g = ones(1,5)/5;  % 5个1平均，核心是"加权求和"的权重的

% 3. 执行卷积（valid模式：只保留完全重叠部分，避免边界失真）
conv_result = conv(f, g, 'valid');

% 4. 绘图对比
figure('Color','w');
subplot(2,1,1);
plot(t, f, 'b-', 'LineWidth',1);
title('原始信号（正弦波+噪声）', 'FontSize',12);
xlabel('时间 t'); ylabel('幅值'); grid on;

subplot(2,1,2);
t_conv = t(3:end-2);  % 卷积后时间轴（去掉前后2个不完全重叠点）
plot(t_conv, conv_result, 'r-', 'LineWidth',1.5);
title('卷积后信号（5点平滑）', 'FontSize',12);
xlabel('时间 t'); ylabel('幅值'); grid on;

二、图像卷积（模糊 / 锐化效果）

Matlab 复制代码

% 1. 读取图像（MATLAB内置示例图）
img = imread('peppers.png');
img_gray = rgb2gray(img);  % 转为灰度图（简化计算）

% 2. 定义卷积核（两种效果可选）
blur_kernel = [1 1 1; 1 1 1; 1 1 1]/9;  % 3x3模糊核（平均滤波）
sharpen_kernel = [0 -1 0; -1 5 -1; 0 -1 0];  % 3x3锐化核（增强边缘）

% 3. 执行图像卷积（使用imfilter，自动处理边界）
img_blur = imfilter(img_gray, blur_kernel, 'replicate');  % 模糊处理
img_sharpen = imfilter(img_gray, sharpen_kernel, 'replicate');  % 锐化处理

% 4. 绘图对比
figure('Color','w');
subplot(1,3,1); imshow(img_gray); title('原始灰度图', 'FontSize',12);
subplot(1,3,2); imshow(img_blur); title('卷积模糊效果', 'FontSize',12);
subplot(1,3,3); imshow(img_sharpen); title('卷积锐化效果', 'FontSize',12);

核心效果说明

信号卷积

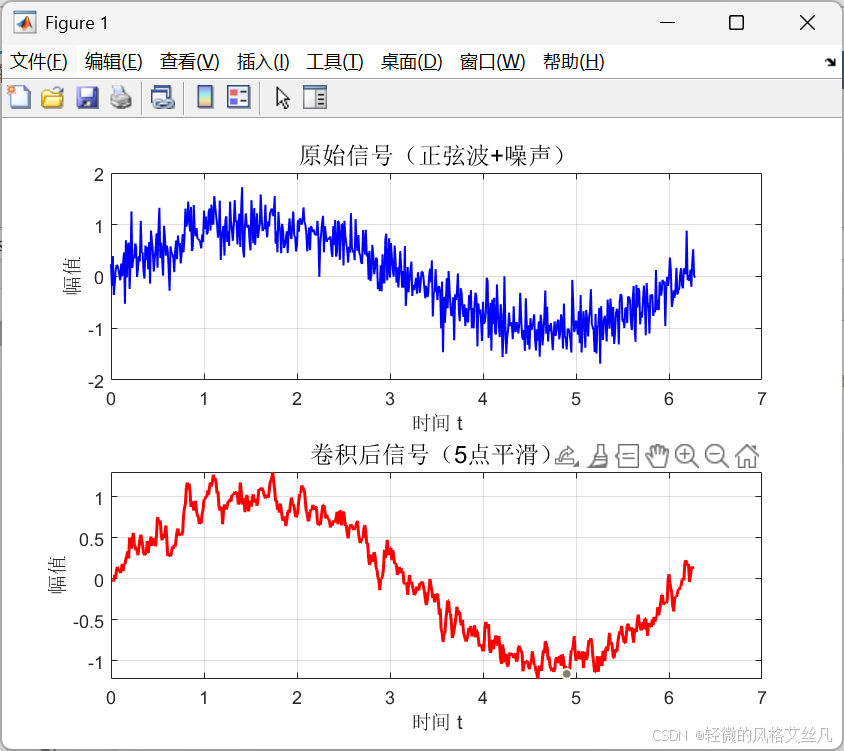
红色曲线比蓝色曲线平滑，印证了卷积 "加权滑动平均" 的本质 ------ 用卷积核的权重 "中和" 噪声；

图像卷积

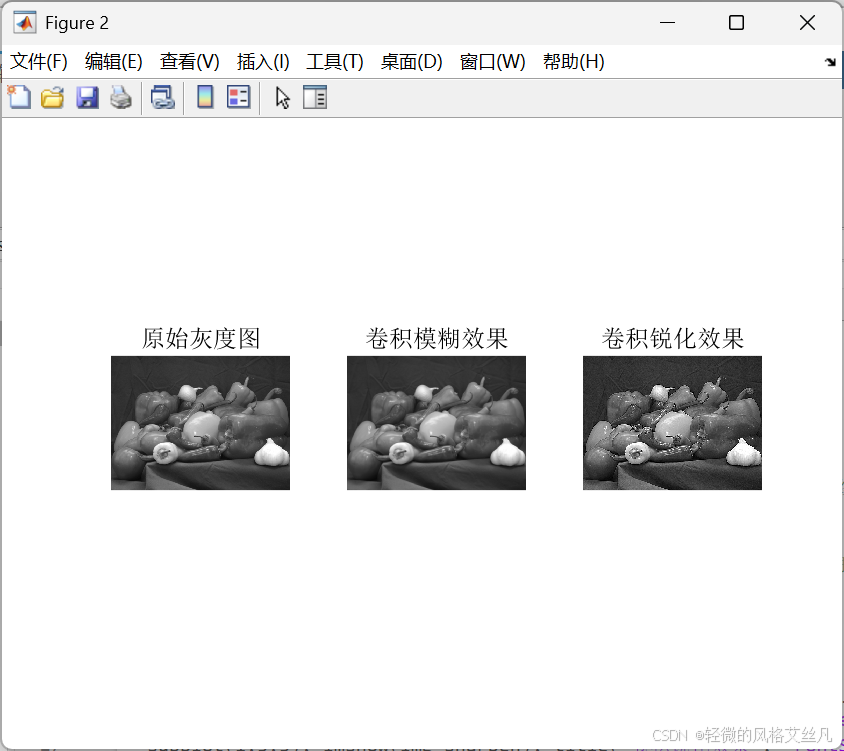
模糊核让像素和周边平均，锐化核通过增强中心像素、抑制周边，突出边缘细节。

卷积与拉氏变换

这个可能偏向于数字信号处理或控制原理。

卷积和拉普拉斯变换（简称 "拉氏变换"）是信号处理里的 "黄金搭档"------ 拉氏变换能把复杂的时域卷积运算 ，直接转换成简单的复频域乘法运算，大幅降低计算难度。

一、核心关系：卷积定理（拉氏变换版）

这是两者关联的核心，一句话说清：两个信号在时域的卷积，其拉氏变换等于这两个信号各自拉氏变换在复频域的乘积

用公式表示更清晰（设信号 f(t)、g(t) 的拉氏变换分别为 F(s)=L[f(t)]、G(s)=L[g(t)]）：L[f(t)∗g(t)]=F(s)⋅G(s)反过来也成立（逆变换）：L−1[F(s)⋅G(s)]=f(t)∗g(t)注：f(t)∗g(t) 表示时域卷积，即 ∫0tf(τ)g(t−τ)dτ（因果信号场景）。

二、为什么这个关系有用？------ 时域难算，频域好算

举个直观例子：假设要计算两个信号的卷积 f(t)∗g(t)，时域里需要做 "滑动、相乘、积分" 三步，尤其是复杂信号（如指数信号、分段信号），积分过程又繁琐又容易出错。

但用拉氏变换后，步骤变成：

分别求 f(t)、g(t) 的拉氏变换 F(s)、G(s)（查拉氏变换表就能搞定）；
复频域里直接做乘法：H(s)=F(s)⋅G(s)；
对 H(s) 做逆拉氏变换，得到的就是时域卷积结果 f(t)∗g(t)。

相当于把 "积分运算" 转换成了 "乘法运算"，难度直接降一个档次！

三、典型应用：线性系统响应计算

这是两者结合最常用的场景 ------ 线性时不变（LTI）系统中，系统输出 = 输入信号 * 系统单位冲激响应（时域卷积）。

用拉氏变换简化后：

输入信号 x(t) → 拉氏变换 X(s)；
系统单位冲激响应 h(t) → 拉氏变换 H(s)（也称 "系统函数"）；
输出信号的拉氏变换 Y(s)=X(s)⋅H(s)；
逆拉氏变换得输出 y(t)=L−1[X(s)⋅H(s)]。

比如一个 RC 电路（系统），输入是阶跃信号，想求电容电压（输出），用卷积定理算比直接积分时域响应简单多了。

数学公式

离散卷积 vs 连续卷积

咱们之前用的都是离散卷积 （信号是离散的点，比如时间 t 取 0.01 步长，图像是像素点），而卷积还有连续卷积（信号是连续函数，比如 f (t)=sin (t)）------ 两者本质一样，只是计算方式不同。

连续卷积公式：f(t)∗g(t)=∫−∞+∞f(τ)g(t−τ)dτ（积分代替离散求和）；
离散卷积公式：f(n)∗g(n)=∑k=−∞+∞f(k)g(n−k)（求和代替积分）；
适用场景：连续卷积多用于理论分析（比如推导系统响应公式），离散卷积多用于工程实现（比如代码里处理信号、图像）。

卷积的 "交换律、结合律"

卷积有两个实用的运算规律，能简化计算：

交换律：f∗g=g∗f → 用 "信号 f 卷核 g" 和 "核 g 卷信号 f" 结果一样。比如用 5 点平滑核卷噪声正弦波，和用噪声正弦波卷 5 点平滑核，结果完全相同；
结合律：(f∗g)∗h=f∗(g∗h) → 先卷 g 再卷 h，和先卷 g*h 再卷 f 一样。比如图像先模糊（卷模糊核）再锐化（卷锐化核），等于卷 "模糊核 × 锐化核"（复频域乘法）的结果。

卷积神经网络

卷积神经网络（CNN）是一种专门处理图像、视频等网格结构数据的深度学习模型，核心是用 "卷积" 替代传统全连接，高效提取图像特征，就像给电脑装了一双 "会看东西的眼睛"。

一、核心特点：为啥适合看图像？

局部感知：只关注图像上的局部区域（比如 3×3 像素块），就像人看东西先盯细节再拼整体，符合视觉规律；
参数共享：一个 "特征探测器"（卷积核）在全图复用，不用给每个像素单独设参数，大幅减少计算量；
平移不变性：不管猫在图像左边还是右边，都能识别出是猫，抗干扰能力强。

二、基本结构：从像素到识别的 3 步走

就像一条 "特征提纯流水线"，核心由 3 类层组成：

卷积层：用卷积核（比如 3×3 大小）在图像上滑动，提取边缘、纹理、颜色块等基础特征，输出 "特征图"；
池化层：对特征图 "压缩瘦身"（比如取 2×2 区域最大值），保留关键特征，减少数据量，让模型更鲁棒；
全连接层：把压缩后的特征图压成一维向量，做最终判断（比如 "这是猫""这是狗"，输出类别概率）。

三、工作原理：怎么 "看懂" 一张图？

以识别猫为例，过程像搭积木：

浅层卷积：提取低级特征（猫的轮廓边缘、毛色块）；
中层卷积：组合低级特征（拼出猫的眼睛、耳朵、鼻子）；
深层卷积：组合中层特征（拼出完整猫脸）；
全连接层：根据猫脸特征，判断 "这是猫" 的概率。

四、常见应用

生活中到处都有它的身影：

图像分类（识别照片里的物体）、人脸识别（手机解锁）；
目标检测（外卖 APP 识别骑手位置）、图像分割（医疗 CT 识别肿瘤）；
风格迁移（把照片改成油画风）、自动驾驶（识别行人和车辆）。