权重初始化方法详解

权重初始化是深度学习模型训练中至关重要的一环。不恰当的初始化会导致：

• 梯度消失问题 (Vanishing Gradient)
• 梯度爆炸问题 (Exploding Gradient)
• 对称性破坏问题 (Symmetry Breaking)
• 训练不稳定 (Training Instability)

---

1. 全零初始化 (Zero Initialization)

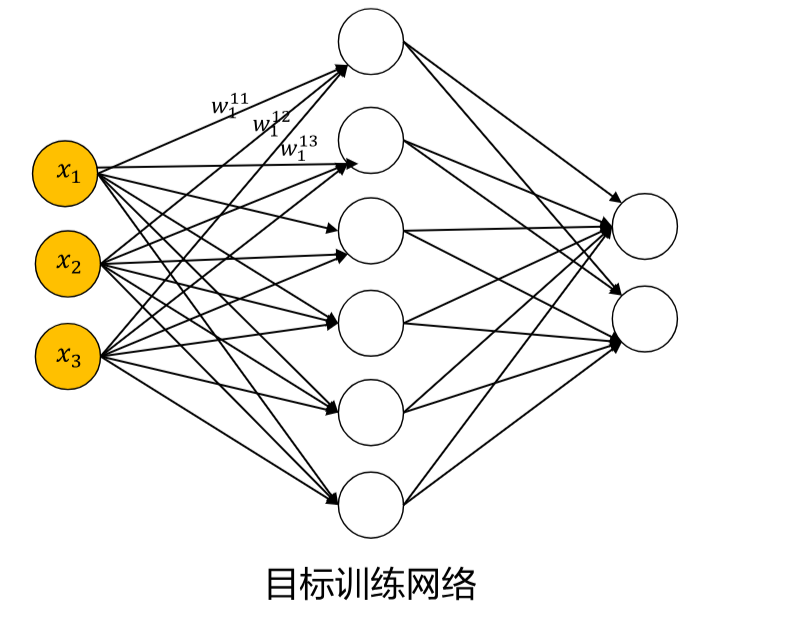
1.1 核心概念

将所有权重参数初始化为0。

1.2 数学表达

对于权重矩阵 W∈Rn×mW \in \mathbb{R}^{n \times m}W∈Rn×m：
Wij=0∀i,j W_{ij} = 0 \quad \forall i,j Wij=0∀i,j

对于偏置项 b∈Rmb \in \mathbb{R}^{m}b∈Rm：
bj=0∀j b_j = 0 \quad \forall j bj=0∀j

1.3 前向传播分析

考虑一个简单的神经网络层：
z=Wx+b z = Wx + b z=Wx+b

其中 x∈Rnx \in \mathbb{R}^{n}x∈Rn 是输入，W=0W = 0W=0，b=0b = 0b=0，则：
z=0⋅x+0=0 z = 0 \cdot x + 0 = 0 z=0⋅x+0=0

输出激活值：
a=σ(z)=σ(0) a = \sigma(z) = \sigma(0) a=σ(z)=σ(0)

其中 σ\sigmaσ 是激活函数。

1.4 反向传播分析

损失函数 ( L ) 对权重的梯度：
∂L∂Wij=∂L∂zj⋅∂zj∂Wij=δj⋅xi \frac{\partial L}{\partial W_{ij}} = \frac{\partial L}{\partial z_j} \cdot \frac{\partial z_j}{\partial W_{ij}} = \delta_j \cdot x_i ∂Wij∂L=∂zj∂L⋅∂Wij∂zj=δj⋅xi

其中 δj=∂L∂zj\delta_j = \frac{\partial L}{\partial z_j}δj=∂zj∂L 是误差项。

由于所有神经元的输入相同（都为0），它们的误差项 ( \delta_j ) 也相同：
δ1=δ2=⋯=δm \delta_1 = \delta_2 = \cdots = \delta_m δ1=δ2=⋯=δm

因此所有权重的梯度更新相同：
ΔWij=−η⋅δ⋅xi∀j \Delta W_{ij} = -\eta \cdot \delta \cdot x_i \quad \forall j ΔWij=−η⋅δ⋅xi∀j

其中 η\etaη 是学习率。

1.5 问题与缺陷

1. 对称性问题 (Symmetry Problem)：所有神经元始终学习相同的特征
2. 打破学习动力：网络无法学习有意义的特征表示
3. 梯度为零：对于某些激活函数（如ReLU），零输入导致零梯度

1.6 适用场景

• 仅用于教学，说明为什么需要更好的初始化方法
• 有时用于偏置项的初始化

---

2. 随机初始化 (Random Initialization)

2.1 核心概念

从概率分布中随机采样权重值，打破神经元的对称性。

2.2 常用方法

2.2.1 均匀分布初始化

Wij∼U(−a,a) W_{ij} \sim U(-a, a) Wij∼U(−a,a)

其中 U(−a,a)U(-a, a)U(−a,a) 表示在区间 [−a,a][-a, a][−a,a]上的均匀分布。

2.2.2 正态分布初始化

Wij∼N(0,σ2) W_{ij} \sim \mathcal{N}(0, \sigma^2) Wij∼N(0,σ2)

其中 N(0,σ2)\mathcal{N}(0, \sigma^2)N(0,σ2)表示均值为0、方差为 σ2\sigma^2σ2的正态分布。

2.3 方差分析

考虑单层网络的前向传播：
zj=∑i=1nWjixi+bj z_j = \sum_{i=1}^{n} W_{ji} x_i + b_j zj=i=1∑nWjixi+bj

假设：

• WjiW_{ji}Wji独立同分布，均值为0，方差为 Var(W)\text{Var}(W)Var(W)
• xix_ixi 独立同分布，均值为0，方差为 Var(x)\text{Var}(x)Var(x)
• WWW与 xxx 相互独立

则输出 zjz_jzj 的方差：
Var(zj)=Var(∑i=1nWjixi)=∑i=1nVar(Wjixi) \text{Var}(z_j) = \text{Var}\left(\sum_{i=1}^{n} W_{ji} x_i\right) = \sum_{i=1}^{n} \text{Var}(W_{ji} x_i) Var(zj)=Var(i=1∑nWjixi)=i=1∑nVar(Wjixi)

由于 ( W ) 和 ( x ) 独立：
Var(Wjixi)=Var(Wji)⋅Var(xi)=Var(W)⋅Var(x) \text{Var}(W_{ji} x_i) = \text{Var}(W_{ji}) \cdot \text{Var}(x_i) = \text{Var}(W) \cdot \text{Var}(x) Var(Wjixi)=Var(Wji)⋅Var(xi)=Var(W)⋅Var(x)

因此：
Var(zj)=n⋅Var(W)⋅Var(x) \text{Var}(z_j) = n \cdot \text{Var}(W) \cdot \text{Var}(x) Var(zj)=n⋅Var(W)⋅Var(x)

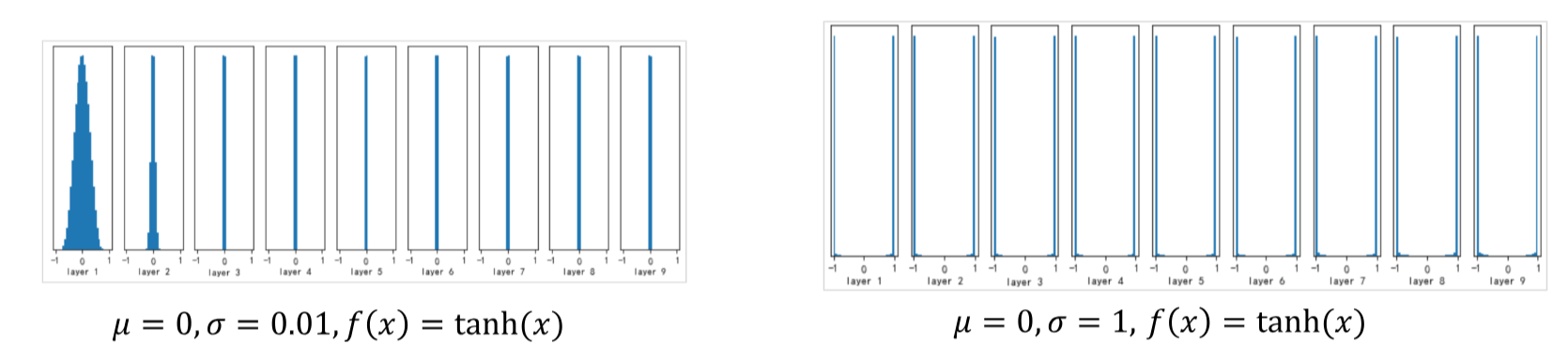
2.4 问题与挑战

• 方差累积：在深度网络中，方差随层数指数增长或衰减
• 梯度不稳定：需要手动调整初始化尺度
• 超参数敏感 ：初始化尺度成为需要调优的超参数
  

---

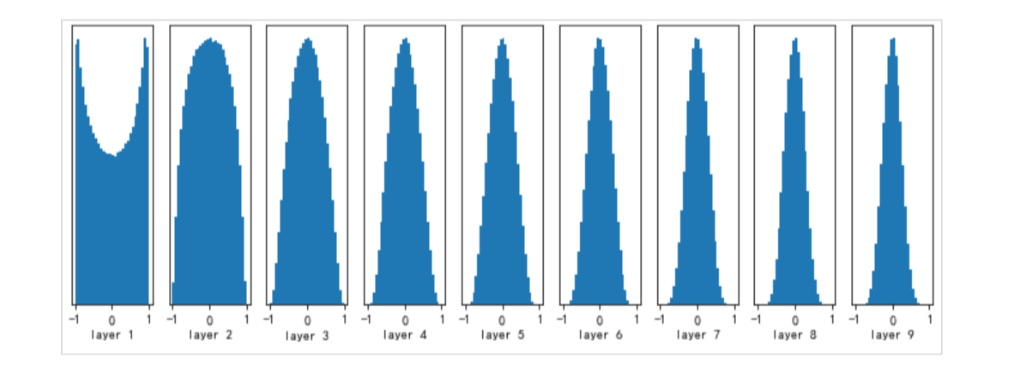
3. Xavier初始化 (Glorot初始化)

3.1 提出背景

由Xavier Glorot和Yoshua Bengio在2010年提出，旨在解决sigmoid和tanh激活函数的初始化问题。

3.2 核心思想

保持前向传播 和反向传播中信号的方差一致。

3.3 数学推导

3.3.1 前向传播方差分析

对于第 lll 层：
z(l)=W(l)a(l−1)+b(l) z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)} z(l)=W(l)a(l−1)+b(l)

其中 a(l−1)=σ(z(l−1))a^{(l-1)} = \sigma(z^{(l-1)})a(l−1)=σ(z(l−1))。

假设：

• Wij(l)W_{ij}^{(l)}Wij(l) 独立同分布，均值为0，方差为 Var(W(l))\text{Var}(W^{(l)})Var(W(l))
• ai(l−1)a_i^{(l-1)}ai(l−1) 独立同分布，均值为0，方差为 Var(a(l−1))\text{Var}(a^{(l-1)})Var(a(l−1))
• W(l)W^{(l)}W(l) 与 a(l−1)a^{(l-1)}a(l−1)相互独立
• 激活函数 σ\sigmaσ 是线性函数（近似成立对于小值）

则：
Var(zj(l))=nl−1⋅Var(W(l))⋅Var(ai(l−1)) \text{Var}(z_j^{(l)}) = n_{l-1} \cdot \text{Var}(W^{(l)}) \cdot \text{Var}(a_i^{(l-1)}) Var(zj(l))=nl−1⋅Var(W(l))⋅Var(ai(l−1))

为了保持方差一致，需要：
nl−1⋅Var(W(l))=1(1) n_{l-1} \cdot \text{Var}(W^{(l)}) = 1 \tag{1} nl−1⋅Var(W(l))=1(1)

3.3.2 反向传播方差分析

考虑损失函数 LLL 对第 l−1l-1l−1 层激活的梯度：
∂L∂ai(l−1)=∑j=1nl∂L∂zj(l)⋅∂zj(l)∂ai(l−1)=∑j=1nlδj(l)⋅Wji(l) \frac{\partial L}{\partial a_i^{(l-1)}} = \sum_{j=1}^{n_l} \frac{\partial L}{\partial z_j^{(l)}} \cdot \frac{\partial z_j^{(l)}}{\partial a_i^{(l-1)}} = \sum_{j=1}^{n_l} \delta_j^{(l)} \cdot W_{ji}^{(l)} ∂ai(l−1)∂L=j=1∑nl∂zj(l)∂L⋅∂ai(l−1)∂zj(l)=j=1∑nlδj(l)⋅Wji(l)

其中 δj(l)=∂L∂zj(l)\delta_j^{(l)} = \frac{\partial L}{\partial z_j^{(l)}}δj(l)=∂zj(l)∂L。

假设 δj(l)\delta_j^{(l)}δj(l) 独立同分布，均值为0，方差为 Var(δ(l))\text{Var}(\delta^{(l)})Var(δ(l))，则：
Var(∂L∂ai(l−1))=nl⋅Var(W(l))⋅Var(δ(l)) \text{Var}\left(\frac{\partial L}{\partial a_i^{(l-1)}}\right) = n_l \cdot \text{Var}(W^{(l)}) \cdot \text{Var}(\delta^{(l)}) Var(∂ai(l−1)∂L)=nl⋅Var(W(l))⋅Var(δ(l))

由于 frac∂L∂ai(l−1)=δi(l−1)⋅σ′(zi(l−1))frac{\partial L}{\partial a_i^{(l-1)}} = \delta_i^{(l-1)} \cdot \sigma'(z_i^{(l-1)})frac∂L∂ai(l−1)=δi(l−1)⋅σ′(zi(l−1))，且 \\sigma'(z_i\^{(l-1)}) \\approx 1（对于线性区域），有：
Var(δ(l−1))≈nl⋅Var(W(l))⋅Var(δ(l)) \text{Var}(\delta^{(l-1)}) \approx n_l \cdot \text{Var}(W^{(l)}) \cdot \text{Var}(\delta^{(l)}) Var(δ(l−1))≈nl⋅Var(W(l))⋅Var(δ(l))

为了保持梯度方差一致，需要：
nl⋅Var(W(l))=1(2) n_l \cdot \text{Var}(W^{(l)}) = 1 \tag{2} nl⋅Var(W(l))=1(2)

3.3.3 折中方案

结合公式(1)和(2)，取调和平均：
Var(W(l))=2nl−1+nl \text{Var}(W^{(l)}) = \frac{2}{n_{l-1} + n_l} Var(W(l))=nl−1+nl2

3.4 具体实现

3.4.1 均匀分布版本

Wij(l)∼U(−6nl−1+nl,6nl−1+nl) W_{ij}^{(l)} \sim U\left(-\frac{\sqrt{6}}{\sqrt{n_{l-1} + n_l}}, \frac{\sqrt{6}}{\sqrt{n_{l-1} + n_l}}\right) Wij(l)∼U(−nl−1+nl 6 ,nl−1+nl 6 )

方差为：
Var(W(l))=(6nl−1+nl)23=2nl−1+nl \text{Var}(W^{(l)}) = \frac{\left(\frac{\sqrt{6}}{\sqrt{n_{l-1} + n_l}}\right)^2}{3} = \frac{2}{n_{l-1} + n_l} Var(W(l))=3(nl−1+nl 6 )2=nl−1+nl2

3.4.2 正态分布版本

Wij(l)∼N(0,2nl−1+nl) W_{ij}^{(l)} \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_{l-1} + n_l}}\right) Wij(l)∼N(0,nl−1+nl2 )

3.5 代码实现

import numpy as np

def xavier_uniform_init(n_in, n_out):
    """Xavier均匀分布初始化"""
    limit = np.sqrt(6 / (n_in + n_out))
    return np.random.uniform(-limit, limit, size=(n_in, n_out))

def xavier_normal_init(n_in, n_out):
    """Xavier正态分布初始化"""
    std = np.sqrt(2 / (n_in + n_out))
    return np.random.normal(0, std, size=(n_in, n_out))

3.6 适用场景

• 激活函数：tanh, sigmoid, softsign
• 不适用于：ReLU及其变种

---

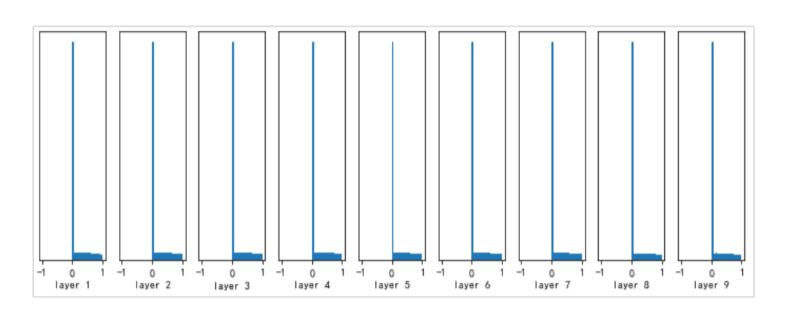
4. He初始化 (MSRA初始化)

4.1 提出背景

由Kaiming He等人在2015年提出，专门针对ReLU激活函数及其变种设计。

4.2 核心思想

考虑ReLU激活函数将一半的输入置零的特性。

4.3 数学推导

4.3.1 ReLU的方差特性

对于ReLU激活函数：
ReLU(x)=max⁡(0,x) \text{ReLU}(x) = \max(0, x) ReLU(x)=max(0,x)

假设输入 ( x ) 服从均值为0的对称分布，则ReLU输出的期望：
E[ReLU(x)]=12E[∣x∣] \mathbb{E}[\text{ReLU}(x)] = \frac{1}{2} \mathbb{E}[|x|] E[ReLU(x)]=21E[∣x∣]

输出的方差：
Var(ReLU(x))=E[ReLU(x)2]−E[ReLU(x)]2 \text{Var}(\text{ReLU}(x)) = \mathbb{E}[\text{ReLU}(x)^2] - \mathbb{E}[\text{ReLU}(x)]^2 Var(ReLU(x))=E[ReLU(x)2]−E[ReLU(x)]2

由于 ReLU(x)2=ReLU(x2)\text{ReLU}(x)^2 = \text{ReLU}(x^2)ReLU(x)2=ReLU(x2)，且对于对称分布有 E[ReLU(x)]=12E[∣x∣]\mathbb{E}[\text{ReLU}(x)] = \frac{1}{2} \mathbb{E}[|x|]E[ReLU(x)]=21E[∣x∣]，可得：
Var(ReLU(x))≈12Var(x) \text{Var}(\text{ReLU}(x)) \approx \frac{1}{2} \text{Var}(x) Var(ReLU(x))≈21Var(x)

4.3.2 前向传播方差分析

对于第 lll 层：
z(l)=W(l)a(l−1)+b(l) z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)} z(l)=W(l)a(l−1)+b(l)

其中 a(l−1)=ReLU(z(l−1))a^{(l-1)} = \text{ReLU}(z^{(l-1)})a(l−1)=ReLU(z(l−1))。

假设：

• Wij(l)W_{ij}^{(l)}Wij(l) 独立同分布，均值为0，方差为 Var(W(l))\text{Var}(W^{(l)})Var(W(l))
• ai(l−1)a_i^{(l-1)}ai(l−1)独立同分布，均值为0，方差为 Var(a(l−1))\text{Var}(a^{(l-1)})Var(a(l−1))

则：
Var(zj(l))=nl−1⋅Var(W(l))⋅Var(ai(l−1)) \text{Var}(z_j^{(l)}) = n_{l-1} \cdot \text{Var}(W^{(l)}) \cdot \text{Var}(a_i^{(l-1)}) Var(zj(l))=nl−1⋅Var(W(l))⋅Var(ai(l−1))

由于 ReLU 使方差减半：
Var(ai(l−1))=12Var(zi(l−1)) \text{Var}(a_i^{(l-1)}) = \frac{1}{2} \text{Var}(z_i^{(l-1)}) Var(ai(l−1))=21Var(zi(l−1))

为了保持方差一致，需要：
nl−1⋅Var(W(l))⋅12=1 n_{l-1} \cdot \text{Var}(W^{(l)}) \cdot \frac{1}{2} = 1 nl−1⋅Var(W(l))⋅21=1

即：
Var(W(l))=2nl−1 \text{Var}(W^{(l)}) = \frac{2}{n_{l-1}} Var(W(l))=nl−12

4.3.3 反向传播分析

类似地，在反向传播中也需要考虑ReLU的影响，最终得到相同的结论。

4.4 具体实现

4.4.1 均匀分布版本

Wij(l)∼U(−6nl−1,6nl−1) W_{ij}^{(l)} \sim U\left(-\frac{\sqrt{6}}{\sqrt{n_{l-1}}}, \frac{\sqrt{6}}{\sqrt{n_{l-1}}}\right) Wij(l)∼U(−nl−1 6 ,nl−1 6 )

方差为：
Var(W(l))=(6nl−1)23=2nl−1 \text{Var}(W^{(l)}) = \frac{\left(\frac{\sqrt{6}}{\sqrt{n_{l-1}}}\right)^2}{3} = \frac{2}{n_{l-1}} Var(W(l))=3(nl−1 6 )2=nl−12

4.4.2 正态分布版本

Wij(l)∼N(0,2nl−1) W_{ij}^{(l)} \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_{l-1}}}\right) Wij(l)∼N(0,nl−12 )

4.5 变种：Leaky ReLU的初始化

对于Leaky ReLU：f(x)=max⁡(αx,x)f(x) = \max(\alpha x, x)f(x)=max(αx,x)，其中 α\alphaα 是负斜率。

输出的方差：
Var(f(x))=1+α22Var(x) \text{Var}(f(x)) = \frac{1 + \alpha^2}{2} \text{Var}(x) Var(f(x))=21+α2Var(x)

因此初始化方差应为：
Var(W(l))=2(1+α2)nl−1 \text{Var}(W^{(l)}) = \frac{2}{(1 + \alpha^2) n_{l-1}} Var(W(l))=(1+α2)nl−12

4.6 代码实现

import numpy as np

def he_uniform_init(n_in, n_out, a=0):
    """He均匀分布初始化"""
    # a是Leaky ReLU的负斜率，对于标准ReLU，a=0
    if a == 0:  # 标准ReLU
        limit = np.sqrt(6 / n_in)
    else:  # Leaky ReLU
        limit = np.sqrt(6 / ((1 + a**2) * n_in))
    return np.random.uniform(-limit, limit, size=(n_in, n_out))

def he_normal_init(n_in, n_out, a=0):
    """He正态分布初始化"""
    if a == 0:  # 标准ReLU
        std = np.sqrt(2 / n_in)
    else:  # Leaky ReLU
        std = np.sqrt(2 / ((1 + a**2) * n_in))
    return np.random.normal(0, std, size=(n_in, n_out))

4.7 适用场景

• 激活函数：ReLU, Leaky ReLU, PReLU, ELU
• 现代深度学习的首选初始化方法

---

总结与对比

初始化方法	提出年份	核心思想	适用激活函数	方差公式	均匀分布范围
全零初始化	-	简单但无效	无	Var(W)=0\text{Var}(W) = 0Var(W)=0	[−0,0][-0, 0][−0,0]
随机初始化	-	打破对称性	需手动调整	Var(W)=σ2\text{Var}(W) = \sigma^2Var(W)=σ2	[−σ3,σ3][-\sigma\sqrt{3}, \sigma\sqrt{3}][−σ3 ,σ3 ]
Xavier初始化	2010	保持前后向传播方差	tanh, sigmoid	Var(W)=2nin+nout\text{Var}(W) = \frac{2}{n_{\text{in}} + n_{\text{out}}}Var(W)=nin+nout2	[−6nin+nout,6nin+nout]\left[-\frac{\sqrt{6}}{\sqrt{n_{\text{in}} + n_{\text{out}}}}, \frac{\sqrt{6}}{\sqrt{n_{\text{in}} + n_{\text{out}}}}\right][−nin+nout 6 ,nin+nout 6 ]
He初始化	2015	考虑ReLU特性	ReLU及其变种	Var(W)=2nin\text{Var}(W) = \frac{2}{n_{\text{in}}}Var(W)=nin2	[−6nin,6nin]\left[-\frac{\sqrt{6}}{\sqrt{n_{\text{in}}}}, \frac{\sqrt{6}}{\sqrt{n_{\text{in}}}}\right][−nin 6 ,nin 6 ]

实践建议

1. 默认选择 ：对于使用ReLU的现代网络，优先选择He初始化
2. 传统网络 ：对于使用tanh或sigmoid的网络，使用Xavier初始化
3. 卷积网络 ：对于卷积层，nin=kernel_width×kernel_height×input_channelsn_{\text{in}} = \text{kernel\_width} \times \text{kernel\_height} \times \text{input\_channels}nin=kernel_width×kernel_height×input_channels
4. 框架实现 ：
   • PyTorch: nn.init.xavier_uniform_(), nn.init.kaiming_uniform_()
   • TensorFlow: glorot_uniform_initializer, he_normal_initializer

理论意义

正确的初始化方法确保了：

• 信号在前向传播中保持适当的幅度
• 梯度在反向传播中保持稳定
• 训练过程快速收敛且稳定
• 模型能够学习有意义的特征表示

这些初始化方法的理论基础深刻影响了深度学习的发展，使得训练更深的神经网络成为可能。