卷积神经网络(Convolutional Neural Network, CNN)是深度学习中最成功的网络结构之一,广泛应用于计算机视觉、语音识别、自然语言处理等领域。CNN 的核心思想是通过"局部感知、权值共享、层次特征提取"来自动学习数据中的空间结构特征。
卷积(Convolution)
卷积的基本原理
卷积操作是 CNN 的核心。其思想源自信号处理领域的卷积运算,用于在输入特征图(Feature Map)上滑动小窗口(卷积核)以提取局部特征。
对于二维输入信号 X(如图像),卷积核 K 的计算方式为:
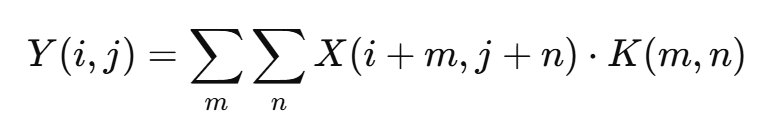
其中 Y(i,j) 表示卷积输出的像素值。
在 CNN 中,卷积层的计算通常引入步幅(stride)和填充(padding):
- Stride(步幅):卷积核滑动的步长,决定输出的缩放比例。
- Padding(填充):在输入边缘补零,用于控制输出尺寸,使特征图不因卷积而过度缩小。
卷积的三大特性
- 局部连接(Local Connectivity)
每个卷积核仅感知输入图像的一小块区域,有助于捕获局部特征。 - 权值共享(Weight Sharing)
同一个卷积核在不同空间位置共享参数,显著减少网络参数数量。 - 平移不变性(Translation Invariance)
卷积结构对图像平移具有一定的鲁棒性,即相同特征在不同位置仍能被识别。
多通道卷积
当输入有多个通道(如 RGB 图像)时,卷积核也会相应地拥有相同数量的通道维度。例如,一个 3×3 的卷积核在三通道输入下其实是 3×3×3 的三维权重矩阵。计算方式为:
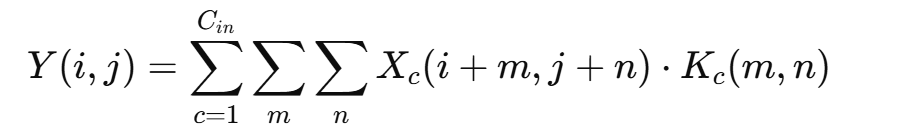
卷积层通常有多个卷积核,输出多个特征图,从而形成深度特征。
卷积的计算流程
- 输入图像(或上一层特征图)进入卷积层。
- 每个卷积核依次在输入上滑动,执行逐元素乘加操作。
- 所有通道卷积结果求和,得到单个输出特征图。
- 对所有卷积核重复上述步骤,形成多个输出通道。
- 输出特征图送入下一层网络。
归一化(Normalization)
归一化的必要性
在神经网络中,随着层数的加深,数据的分布容易发生"漂移"(即 内部协变量偏移,Internal Covariate Shift),导致梯度不稳定、训练收敛变慢或网络容易陷入梯度消失。
为此,人们引入了归一化(Normalization)技术来稳定数据分布,使输入到每一层的数据具有相对一致的均值与方差,从而提升网络的收敛速度与泛化能力。
常见的归一化方法
| 方法 | 归一化范围 | 常用于 |
|---|---|---|
| Batch Normalization(BN) | 对每个通道的 mini-batch 归一化 | 卷积网络 |
| Layer Normalization(LN) | 对单个样本的所有神经元归一化 | Transformer |
| Instance Normalization(IN) | 对单个样本的每个通道归一化 | 风格迁移 |
| Group Normalization(GN) | 将通道分组后归一化 | 小 batch 场景 |
Batch Normalization(BN)原理
BN 在每一层的输入上执行如下变换:
设输入为 x1,x2,...,xm,则:
-
计算均值与方差
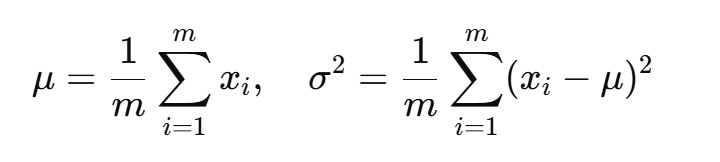
-
标准化
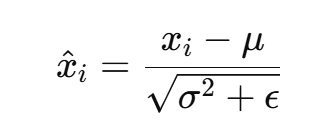
-
线性缩放与平移(可学习参数)
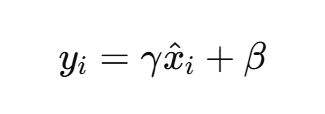
其中:
- γ、β 是可学习参数,用于恢复网络表达能力;
- ϵ 是防止除零的小常数。
在训练阶段,BN 使用当前 batch 的统计值;
在推理阶段,使用整个训练集的移动平均统计值。
BN 的作用
- 加速收敛
通过保持输入分布稳定,允许使用更大学习率。 - 防止梯度爆炸/消失
标准化后数据在合理范围内,有助于梯度稳定。 - 具有轻微正则化效果
对小批量噪声的引入可减少过拟合。 - 提高训练稳定性与泛化性
BN 在卷积中的应用流程
对于卷积层输出 Z=W∗X+b,BN 的处理过程如下:
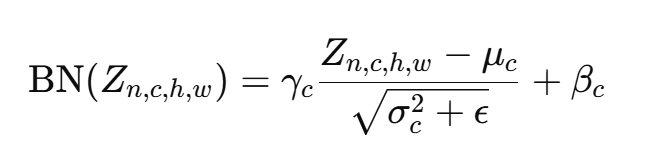
即:
- 按通道计算均值与方差;
- 对每个通道分别归一化;
- 再进行缩放与平移;
- 输出送入激活函数层(如 ReLU)。
ReLU 激活函数
激活函数的意义
神经网络如果仅由线性运算(如卷积与全连接)组成,无论层数多深,整体仍等价于一个线性变换,无法表达复杂非线性映射。因此,需要**激活函数(Activation Function)**引入非线性因素,使网络具备更强的表达能力。
ReLU 定义与形式
ReLU(Rectified Linear Unit)是目前最常用的激活函数,其定义为:
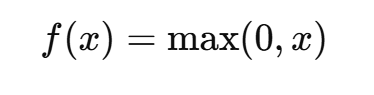
即:
- 当 x>0 时,输出 x;
- 当 x≤0 时,输出 0。
ReLU 的优点
- 计算简单:只需比较操作,无需指数或除法。
- 梯度传播稳定:正区间梯度恒为 1,避免梯度消失问题。
- 稀疏激活:大量神经元被"置零",提高网络表达的稀疏性与泛化能力。
- 加快收敛:梯度更大,训练速度快。
ReLU 的缺陷与改进
缺陷:
- 当输入长期为负时,神经元将永远输出 0(称为"死亡 ReLU"现象)。
改进版本:
| 函数 | 定义 | 特点 |
|---|---|---|
| Leaky ReLU | f(x)=max(0.01x,x) | 允许负区间有微弱梯度 |
| Parametric ReLU(PReLU) | f(x)=max(ax,x),a可学习 | 自适应负区间斜率 |
| ELU | f(x)=x if x>0, else α(ex−1) | 平滑过渡,负区间输出非零 |
| GELU / SiLU | 平滑近似形式,常用于 Transformer | 更适合复杂分布 |
卷积 + BN + ReLU 全流程
现代 CNN 通常采用这样的层结构:
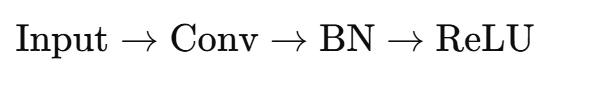
这一组合(Conv-BN-ReLU)几乎构成了所有深度网络(如 ResNet、VGG、MobileNet)的基本单元。
数据流动顺序
- 卷积层(Conv)
提取局部特征,生成中间特征图。 - 批归一化层(BN)
规范化卷积输出,使分布稳定。 - ReLU 激活层
引入非线性,提高特征表达能力。
流程示意(以单个通道为例)
-
输入图像块 X;
-
使用卷积核 W 计算输出 Z=W∗X+b;
-
对 Z 执行 BN:
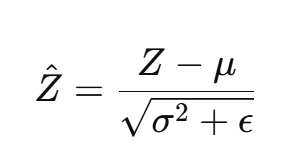
-
线性变换:
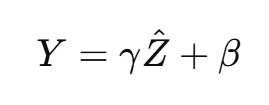
-
通过 ReLU:
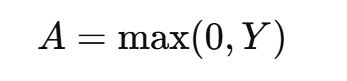
-
输出 AAA 进入下一层卷积。
为什么顺序是 Conv → BN → ReLU
原因如下:
- BN 作用于卷积输出,能直接稳定卷积层输出分布;
- 若 BN 放在 ReLU 后,会改变激活分布,使均值偏正;
- 该顺序能最大程度保持梯度稳定性与训练效率;
- 实验上证实 Conv-BN-ReLU 的结构在几乎所有 CNN 中表现最优。
整体工作机制分析
在 CNN 中,卷积层负责抽取特征 ,BN 层负责稳定特征分布 ,ReLU 负责引入非线性。三者协同构成了一个完整的特征提取模块。
从训练角度
- 卷积层通过反向传播不断学习合适的滤波器;
- BN 让每层输入保持标准分布,加快学习;
- ReLU 让梯度信号能更有效传播到前层。
从特征角度
- 卷积核提取局部纹理(边缘、角点等);
- BN 调整不同通道间的尺度,使特征可比较;
- ReLU 强调显著特征,抑制噪声。
从网络稳定性角度
- BN 避免梯度爆炸;
- ReLU 避免过度线性;
- 两者共同提升训练速度与模型收敛性。
ResNet 基础单元
以 ResNet 的 Basic Block 为例,其结构如下:
scss
Input → Conv(3×3) → BN → ReLU → Conv(3×3) → BN → Add(Input) → ReLU该结构展示了卷积、归一化、激活在深度网络中的标准使用方式,并结合残差连接(skip connection)进一步缓解梯度退化问题。
总结
| 模块 | 功能 | 数学形式 | 主要作用 |
|---|---|---|---|
| 卷积层 | 提取局部特征 | Y=W∗X+b | 学习空间结构信息 |
| 归一化层 | 稳定特征分布 | x^=(x−μ)/σ2+ϵ | 加速收敛、防止过拟合 |
| ReLU 激活层 | 引入非线性 | f(x)=max(0,x) | 提高表达能力、加速训练 |
------------ | ------------- | ---------------------- |
| 卷积层 | 提取局部特征 | Y=W∗X+b | 学习空间结构信息 |
| 归一化层 | 稳定特征分布 | x^=(x−μ)/σ2+ϵ | 加速收敛、防止过拟合 |
| ReLU 激活层 | 引入非线性 | f(x)=max(0,x) | 提高表达能力、加速训练 |
三者的组合使 CNN 能够在保持训练稳定性的同时学习复杂的特征层次,是现代深度学习模型性能提升的关键所在。