扫描线1
例题1
有 n n n 根彼此相邻的柱子,宽度为 1 1 1,现给定一个长度为 n n n 的非负整数数组 A A A,其中 A [ i ] A[i] A[i] 表示第 i i i 根柱子的高度。
请问在这个柱状图中,能够找到的最大矩形面积是多少?
题解
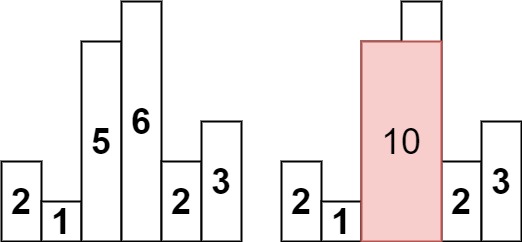
如上图,对于这样的柱状图我们怎么去寻找最大矩形呢?
我们可以每次找出 以 a [ i ] a[i] a[i] 作为高度的最大矩形,答案必然在这些矩形之内。
不难发现以 a [ i ] a[i] a[i] 为高度的最大矩形的右边界必然是 i i i 左侧第一个小于 a [ i ] a[i] a[i] 的位置的右边一格。
同理,以 a [ i ] a[i] a[i] 为高度的最大矩形的左边界必然是 i i i 左侧第一个小于 a [ i ] a[i] a[i] 的位置的右边一格。
求上述左右边界可以用单调栈预处理,对于每个 a [ i ] a[i] a[i] 需要进行下面两个步骤:
- 如果 a [ i ] a[i] a[i] 小于栈顶,说明栈顶的 右边界 就是 i − 1 i-1 i−1,我们不断将栈顶弹出更新它们的右边界,直到不小于栈顶。
- 将 a [ i ] a[i] a[i] 加入栈中。
对于左边界,我们只需要 倒着进行一遍 这个过程就行。
求出每个以 a [ i ] a[i] a[i] 高的最大矩形的左右边界之后,就能统计这个矩形的面积,每次更新最大面积即可。
时间复杂度为 O ( n ) O(n) O(n)。
cpp
#include <bits/stdc++.h>
using namespace std;
//#pragma GCC optimize(2)
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18
int largestRectangleArea(vector<int>& heights) {
vector <int> minStack;
vector <int> L(heights.size(), 0), R(heights.size(), 0);
for (int i = 0; i < heights.size(); i++) {
while (minStack.size() && heights[minStack.back()] > heights[i]) {
R[minStack.back()] = i;
minStack.pop_back();
}
minStack.push_back(i);
}
while (minStack.size()) {
R[minStack.back()] = heights.size();
minStack.pop_back();
}
for (int i = heights.size() - 1; i >= 0; i--) {
while (minStack.size() && heights[minStack.back()] > heights[i]) {
L[minStack.back()] = i + 2;
minStack.pop_back();
}
minStack.push_back(i);
}
while (minStack.size()) {
L[minStack.back()] = 1;
minStack.pop_back();
}
int ans = 0;
for (int i = 0; i < heights.size(); i++) {
ans = max(ans, heights[i] * (R[i] - L[i] + 1));
}
return ans;
}
void slove () {
int n;
cin >> n;
vector <int> heights(n);
for (int i = 0; i < n; i++) {
cin >> heights[i];
}
cout << largestRectangleArea(heights);
}
signed main () {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
slove();
}例题2
给定一个由 0 0 0 和 1 1 1 组成的 n × m n\times m n×m 矩阵,找出其中只包含 1 1 1 的最大矩阵。
数据范围: 1 ≤ n , m ≤ 200 1 \le n,m\le 200 1≤n,m≤200。
题解
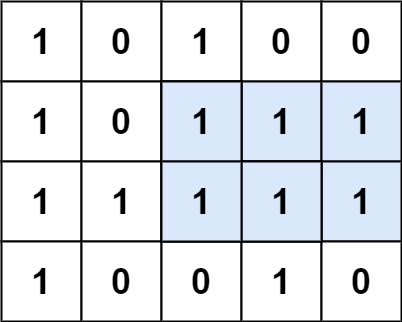
01 01 01 矩阵参考上图,我们可以维护一根长度为 n n n 的扫描线数组 h e i g h t height height,从左到右开始扫描,当扫描到第 j j j 列时对于每一行 i i i 有:
- 若 ( i , j ) (i,j) (i,j) 是 1 1 1,将 h e i g h t [ i ] height[i] height[i] 增加 1 1 1。
- 若 ( i , j ) (i,j) (i,j) 是 0 0 0,令 h e i g h t [ i ] = 0 height[i]=0 height[i]=0。
其中 h e i g h t [ i ] height[i] height[i] 的实际意义就是,以第 j j j 列为底边,第 i i i 行能往左边延伸的最长长度。
所以要计算以 x = j x=j x=j 为底的矩阵中最大的只包含 1 1 1 的子矩阵,我们只需要计算出 h e i g h t height height 中的最大矩形面积就行了,而计算 h e i g h t height height 中的最大矩形面积过程参考例题 1 1 1。
时间复杂 O ( n m ) O(nm) O(nm)。
cpp
#include <bits/stdc++.h>
using namespace std;
//#pragma GCC optimize(2)
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18
int largestRectangleArea(vector<int>& heights) {
vector <int> minStack;
vector <int> L(heights.size(), 0), R(heights.size(), 0);
for (int i = 0; i < heights.size(); i++) {
while (minStack.size() && heights[minStack.back()] > heights[i]) {
R[minStack.back()] = i;
minStack.pop_back();
}
minStack.push_back(i);
}
while (minStack.size()) {
R[minStack.back()] = heights.size();
minStack.pop_back();
}
for (int i = heights.size() - 1; i >= 0; i--) {
while (minStack.size() && heights[minStack.back()] > heights[i]) {
L[minStack.back()] = i + 2;
minStack.pop_back();
}
minStack.push_back(i);
}
while (minStack.size()) {
L[minStack.back()] = 1;
minStack.pop_back();
}
int ans = 0;
for (int i = 0; i < heights.size(); i++) {
ans = max(ans, heights[i] * (R[i] - L[i] + 1));
}
return ans;
}
int maximalRectangle(vector<string>& matrix) {
if (matrix.empty()) return 0;
int n = matrix.size(), m = matrix[0].size();
int ans = 0;
vector <int> heights(n, 0);
for (int j = 0; j < m; j++) {
for (int i = 0; i < n; i++) {
if (matrix[i][j] == '1') heights[i] ++;
else heights[i] = 0;
}
ans = max(ans, largestRectangleArea(heights));
}
return ans;
}
void slove () {
vector<string> matrix;
string s;
while (cin >> s) {
matrix.push_back(s);
}
cout << maximalRectangle(matrix) << endl;
}
signed main () {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
slove();
}例题 3
给定 N N N 头牛的二维坐标,牛分为两个品种,姑且可以看做 − 1 -1 −1 和 1 1 1,希望找到一个最小的矩形,使得矩形内部全是 1 1 1,且矩形内部框住的 1 1 1 最多,如果框柱的 1 1 1 一样多,那么令矩形尽量小。
输出符合条件的最小矩形的面积。
数据范围: 0 ≤ x , y ≤ 1000 0\le x,y\le 1000 0≤x,y≤1000, 1 ≤ N ≤ 500 1\le N\le 500 1≤N≤500。
题解
不难发现,如果一个矩形能作为答案,那么必然这个矩形的四条边框上具有牛 1 1 1,否则我们总能收缩一条边使得矩形的面积变小,但包围住的牛数量不变。
这题与例题 2 2 2 不同之处在于,这题还具有 空地 这种情况。
离散化
我们先将所有涉及到牛的下标离线收集起来, x x x 坐标放到 p o s X posX posX 里, y y y 坐标放到 p o s Y posY posY 里,对这两个数组进行离散化。
将实际的二维矩阵离散化,保证离散化后的二维矩阵的行数与列数分别与 p o s X posX posX 和 p o s Y posY posY 大小相等。
再对这个离散化后的二维矩阵求二维前缀和,这便于 O ( 1 ) O(1) O(1) 判断某个矩形内有多少牛 1 1 1。
扫描线
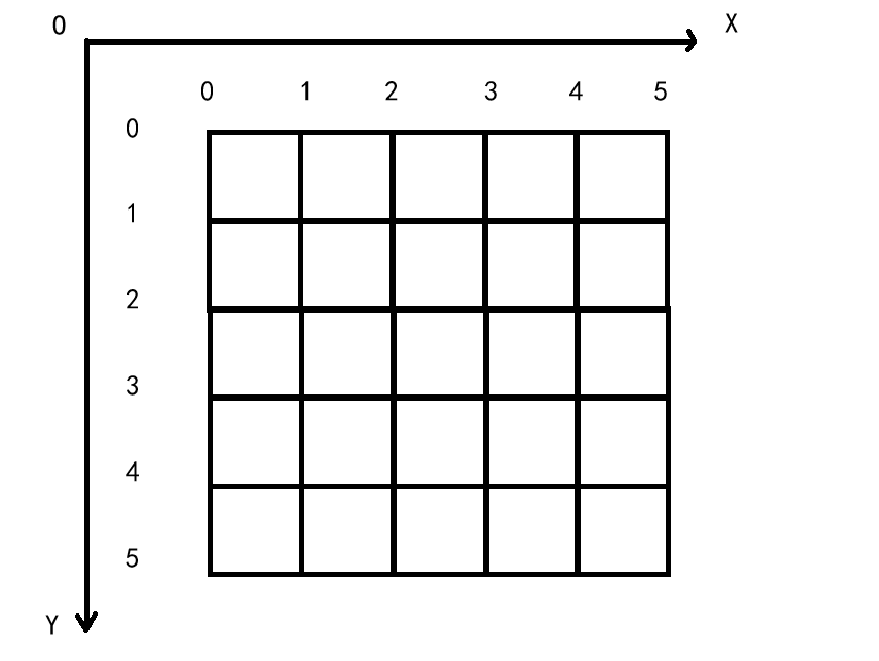
维护一个方向是 x x x 轴正方向 的扫描线数组 h h h,当扫描到 x = j x=j x=j 时有:
- 如果 ( i , j ) (i,j) (i,j) 是牛 1 1 1 或者空地,那么 h [ i ] h[i] h[i] 加 1 1 1。
- 如果 ( i , j ) (i,j) (i,j) 是牛 0 0 0,那么 h [ i ] h[i] h[i] 置为 0 0 0。
在这里 h [ j ] h[j] h[j] 表示从 x = i x=i x=i 这根横线上的 y = j y=j y=j 处出发,往左最多走多远。
如果 h [ j ] = 2 h[j]=2 h[j]=2,那么其实就是从 p o s X [ i ] posX[i] posX[i],走到了 p o s X [ i − h [ j ] + 1 ] posX[i-h[j]+1] posX[i−h[j]+1],在离散化二维矩阵里就是从 x = i x=i x=i 走到了 x = i − h [ j ] + 1 x=i-h[j]+1 x=i−h[j]+1。
此时对 h h h 数组求最大矩形面积,具体求法是枚举 y = j y=j y=j 这条直线矩形内的最长直线,然后分别找出最远的不小于 y = j y=j y=j 长度的上下边界 y = L , y = R y=L,y=R y=L,y=R。
此时我们就得到了一个 粗糙的矩形 ,左边界是 x = i − h [ j ] + 1 x=i-h[j]+1 x=i−h[j]+1,右边界是 x = i x=i x=i,上边界是 y = L y=L y=L,下边界是 y = R y=R y=R,此时我们就可以用二维离散前缀和来求出矩形内牛 1 1 1 的个数(必然不包括牛 − 1 -1 −1)。
之所以被称为粗糙的矩形,是因为这样的矩形的边界处可能是空地,所以我们还需要收缩左边界、上边界、下边界。
所以循环判断当前边界处是否含有 牛 1 1 1,如果不含有,那么向内收缩。
我们每次用这样的矩形来更新答案即可。
cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 1001;
int a[N][N];
vector <int> posX, posY;
vector <vector<int>> s, cow;
// 离散化
void lsh () {
sort(posX.begin(), posX.end());
sort(posY.begin(), posY.end());
posX.erase(unique(posX.begin(), posX.end()), posX.end());
posY.erase(unique(posY.begin(), posY.end()), posY.end());
}
// 预处理二维离散数组
void prefixSum () {
s.assign(posX.size(), vector<int>(posY.size(), 0));
cow.assign(posX.size(), vector<int>(posY.size(), 0));
for (int i = 0; i < posX.size(); i++) {
for (int j = 0; j < posY.size(); j++) {
cow[i][j] = a[posX[i]][posY[j]];
}
}
for (int i = 0; i < posX.size(); i++) {
for (int j = 0; j < posY.size(); j++) {
s[i][j] = (i > 0 ? s[i - 1][j] : 0) +
(j > 0 ? s[i][j - 1] : 0) - (i > 0 && j > 0 ? s[i - 1][j - 1] : 0)
+ cow[i][j];
}
}
}
// 求二维离散数组前缀和
int getSum (int x1, int y1, int x2, int y2) {
return s[x2][y2] -
(x1 > 0 ? s[x1 - 1][y2] : 0) -
(y1 > 0 ? s[x2][y1 - 1] : 0) +
(x1 > 0 && y1 > 0 ? s[x1 - 1][y1 - 1] : 0);
}
void solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
int x, y;
cin >> x >> y;
char ch;
cin >> ch;
if (ch == 'H') a[x][y] = 1;
else a[x][y] = -1;
posX.push_back(x);
posY.push_back(y);
}
lsh();
prefixSum();
int maxCow = 0;
int minS = 0;
vector <int> h(posY.size(), 0);
for (int i = 0; i < posX.size(); i++) {
// 更新扫描线
for (int j = 0; j < posY.size(); j++) {
if (cow[i][j] != -1) h[j] ++;
else h[j] = 0;
}
// 单调栈求上下边界
vector <int> U(posY.size()), D(posY.size());
vector <int> minStack;
// 求 D
for (int j = 0; j < posY.size(); j++) {
while (minStack.size() && h[minStack.back()] > h[j]) {
D[minStack.back()] = j - 1;
minStack.pop_back();
}
minStack.push_back(j);
}
while (minStack.size()) {
D[minStack.back()] = posY.size() - 1;
minStack.pop_back();
}
// 求 U
for (int j = posY.size() - 1; j >= 0; j--) {
while (minStack.size() && h[minStack.back()] > h[j]) {
U[minStack.back()] = j + 1;
minStack.pop_back();
}
minStack.push_back(j);
}
while (minStack.size()) {
U[minStack.back()] = 0;
minStack.pop_back();
}
// 开始计算粗糙矩形面积
for (int j = 0; j < posY.size(); j++) {
int x1 = i - h[j] + 1, x2 = i;
// 收缩左边界
while (x1 < i) {
bool is_ok = 0;
// 当 x 在左边界,判断左边界是否全是空地
for (int l = U[j]; l <= D[j]; l++) {
if (cow[x1][l] != 0) is_ok = 1;
}
if (is_ok == 0) x1 ++;
else break;
}
// 收缩 上下边界
while (getSum(x1, U[j], i, U[j]) == 0 && U[j] < j) U[j] ++;
while (getSum(x1, D[j], i, D[j]) == 0 && D[j] > j) D[j] --;
int H = posX[x2] - posX[x1];
int wide = posY[D[j]] - posY[U[j]];
int S = H * wide;
int y1 = U[j], y2 = D[j];
int cows = getSum(x1, y1, x2, y2);
if (cows > maxCow) {
maxCow = cows;
minS = S;
} else if (cows == maxCow) {
minS = min(minS, S);
}
}
}
cout << maxCow << endl << minS << endl;
}
signed main() {
solve();
}