【机器学习】监督学习

hrrrrb2025-10-28 14:28

机器学习

Scikit-learn

监督学习

监督学习概念

监督学习的核心定义

监督学习（Supervised Learning）是机器学习的三大核心范式之一（另外两种是无监督学习和强化学习），其核心思想可以用一句话概括：

"用带有标签的样本训练模型，让模型学会特征与标签的关系，从而预测新样本的标签。"

这里的 "监督" 可以理解为：模型在学习过程中，始终有 "标准答案"（标签）作为参考，就像老师监督学生做题 ------ 学生（模型）通过做有答案的例题（训练样本）学习解题规律，然后用学到的规律解答新题目（测试样本）。

监督学习的核心要素

一个完整的监督学习任务包含三个核心要素：

  1. 特征（Features，通常用 X 表示） ：描述样本的属性或输入数据。
    例：预测房价时，"面积、房间数、地段" 是特征；预测学生成绩时，"学习时长、上次成绩" 是特征。
    特征通常是二维数组（shape=(样本数，特征数)），每行代表一个样本，每列代表一个特征。
  2. 标签（Label，通常用 y 表示） ：样本的 "答案" 或目标输出。
    例：房价预测中，"房价" 是标签；垃圾邮件识别中，"是否为垃圾邮件（0/1）" 是标签。
    标签是一维数组（shape=(样本数，)），每个元素对应一个样本的目标值。
  3. 模型（Model） ：学习特征与标签关系的算法。
    模型通过训练数据（X_train, y_train）学习到一个 "映射函数" f ，使得 f (X )≈y，然后用这个函数预测新样本的标签。

监督学习的两大核心任务

根据标签的类型（离散或连续），监督学习可分为两大任务：分类（Classification） 和 回归（Regression）。

任务类型 目标 标签类型 通俗理解 生活案例
分类（Classification） 预测样本属于哪个类别 离散值（如 0/1/2、男 / 女） "做选择题"------ 从有限选项中选答案 垃圾邮件识别（垃圾 / 正常）、疾病诊断（患病 / 健康）、鸢尾花种类识别（3 类）
回归（Regression） 预测样本的连续数值 连续值（如价格、温度） "做填空题"------ 预测具体数值 房价预测（如 500 万、800 万）、温度预测（如 25℃、30℃）、销售额预测

监督学习的流程（与预处理流程衔接）

监督学习的完整流程是对 "数据预处理流程" 的延伸，可总结为：

  1. 数据准备：收集带标签的样本，提取特征 X 和标签 y；
  2. 数据预处理：处理缺失值、缩放特征、编码类别特征（第二模块内容）；
  3. 划分数据集：将数据分为训练集（X_train, y_train）和测试集（X_test, y_test）；
  4. 模型训练 ：用训练集拟合模型（调用 fit(X_train, y_train)），让模型学习 X 到 y 的映射；
  5. 模型预测 ：用训练好的模型预测测试集标签（调用 predict(X_test)）；
  6. 模型评估：用评估指标（如准确率、均方误差）对比预测值与真实标签（y_test），判断模型好坏；
  7. 模型优化：根据评估结果调整模型参数或更换模型，重复训练 - 评估过程。

为什么监督学习是最常用的机器学习范式？

因为现实世界中，大量任务都有明确的 "输入 - 输出" 对应关系（即有标签数据）：

  • 企业有历史销售数据（特征：广告投入、时间；标签：销售额），可用于预测未来销售；
  • 医院有病人病历（特征：症状、年龄；标签：是否患病），可用于辅助诊断；
  • 电商有用户行为数据（特征：浏览时长、点击量；标签：是否购买），可用于推荐商品。

这些场景都天然适合用监督学习解决，因此监督学习是工业界应用最广泛的机器学习方法。

监督学习的本质是 "从已知答案的样本中学习规律，再用规律预测未知答案"。它的核心是 "标签"------ 有标签数据是监督学习的前提，而模型的目标是尽可能准确地捕捉特征与标签之间的真实关系。

分类算法

逻辑回归（Logistic Regression）

逻辑回归是分类任务的 "入门首选"，虽然名字里有 "回归"，但它本质是二分类算法（也可扩展到多分类），核心是通过概率判断样本属于某一类别的可能性。

数学直觉：从线性回归到逻辑回归

线性回归输出的是连续值（如房价），而分类任务需要输出 "类别"（如 0 或 1）。逻辑回归的巧妙之处在于：

  1. 先用线性回归的方式计算特征的加权和： z = w 1 x 1 + w 2 x 2 + . . . + b z=w_1x_1+w_2x_2+...+b z=w1x1+w2x2+...+b（ w w w 是权重， b b b 是偏置）；
  2. 再通过 sigmoid 函数 将 z z z 转换为 [0,1] 之间的概率值：
    P ( y = 1 ∣ x ) = 1 1 + e − z P(y=1∣x)={1 \over 1+e^{−z}} P(y=1∣x)=1+e−z1
    • 当 z → + ∞ z→+∞ z→+∞ 时， P → 1 P→1 P→1（样本大概率属于类别 1）；
    • 当 z → − ∞ z→−∞ z→−∞ 时， P → 0 P→0 P→0（样本大概率属于类别 0）；
    • 当 z = 0 z=0 z=0 时， P = 0.5 P=0.5 P=0.5（临界值）。
  3. 最后用阈值（通常是 0.5）判断类别：若 P ≥ 0.5 P≥0.5 P≥0.5，预测为 1；否则为 0。

代码示例：二分类（判断是否为山鸢尾花）

用 Iris 数据集的简化版（只区分 "是否为山鸢尾花 Setosa"）演示逻辑回归的完整流程：

python 复制代码 
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report

# 1. 加载数据（Iris 包含3类鸢尾花，我们简化为二分类）
iris = load_iris()
X = iris.data  # 特征：花萼长度、宽度，花瓣长度、宽度
y = (iris.target == 0).astype(int)  # 标签：1表示Setosa，0表示其他（二分类）

# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 初始化并训练逻辑回归模型
model = LogisticRegression()  # 默认处理二分类，多分类需指定multi_class参数
model.fit(X_train, y_train)  # 用训练集学习特征与标签的关系

# 4. 预测与评估
y_pred = model.predict(X_test)  # 预测测试集标签
y_pred_proba = model.predict_proba(X_test)  # 输出每个样本属于各类别的概率（[:,1]是属于1的概率）

# 评估指标
print("准确率（Accuracy）：", accuracy_score(y_test, y_pred))
print("\n分类报告（包含精确率、召回率等）：")
print(classification_report(y_test, y_pred))

输出结果解析：

mathematica 复制代码 
准确率（Accuracy）： 1.0

分类报告（包含精确率、召回率等）：
              precision    recall  f1-score   support

           0       1.00      1.00      1.00        26
           1       1.00      1.00      1.00        19

    accuracy                           1.00        45
   macro avg       1.00      1.00      1.00        45
weighted avg       1.00      1.00      1.00        45
  • 准确率（Accuracy）=1.0：测试集 45 个样本全部预测正确；
  • 分类报告中，precision（精确率）、recall（召回率）均为 1.0，说明模型对两类的判断都很完美（Iris 数据集较简单）。

逻辑回归的核心特点：

  • 优点 ：
    1. 输出是概率值，可解释性强（如 "这个样本有 90% 的概率是垃圾邮件"）；
    2. 训练速度快，适合大规模数据；
    3. 可通过正则化（penalty='l1' 或 'l2'）缓解过拟合。
  • 缺点 ：
    1. 只能学习线性关系，对非线性数据拟合能力弱（需手动构造多项式特征）；
    2. 默认是二分类，多分类需特殊处理（multi_class='multinomial'）。
K 最近邻（K-Nearest Neighbors, KNN）

KNN 是最直观的分类算法，它不需要 "训练" 过程，而是在预测时通过 "找邻居" 来判断类别，属于 "惰性学习"（lazy learner）。

核心思想："近朱者赤，近墨者黑"

  1. 当预测一个新样本时，计算它与所有训练样本的 "距离"（如欧氏距离）；
  2. 找出距离最近的 K 个训练样本（这 K 个就是 "邻居"）；
  3. 对这 K 个邻居的标签进行 "投票"：出现次数最多的标签就是新样本的预测类别。

例：若 K=3，3 个邻居的标签是 [1,1,0]，则新样本预测为 1。

代码示例：用 KNN 做鸢尾花分类

python 复制代码 
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

# 1. 加载数据（完整3类鸢尾花，多分类）
iris = load_iris()
X, y = iris.data, iris.target

# 2. 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 初始化KNN模型（K=5）
model = KNeighborsClassifier(n_neighbors=5)  # n_neighbors是核心参数

# 4. "训练"模型（实际是存储训练样本）
model.fit(X_train, y_train)

# 5. 预测与评估
print("测试集准确率：", model.score(X_test, y_test))  # 输出：0.977...（约98%）

参数调优：K 值的影响

n_neighbors（K 值）是 KNN 最关键的参数，直接影响模型效果：

  • K 值太小（如 K=1）：模型容易过拟合（对噪声敏感，邻居中一个异常值就可能影响结果）；
  • K 值太大（如 K = 训练集样本数）：模型会欠拟合（所有样本的邻居都是整个训练集，预测结果永远是多数类）。

通常通过交叉验证选择最优 K 值（后续模块会讲）。

KNN 的核心特点：

  • 优点 ：
    1. 逻辑简单，无需数学推导，容易理解；
    2. 可处理多分类问题，无需额外配置；
    3. 对新数据的适应能力强（新增样本只需加入训练集，无需重新训练）。
  • 缺点 ：
    1. 预测速度慢（需计算与所有训练样本的距离，数据量大时耗时）；
    2. 对高维数据不友好（距离计算在高维空间中会失效，即 "维度灾难"）；
    3. 对不平衡数据敏感（多数类样本会主导投票）。
决策树（DecisionTreeClassifier）

核心思想：层层提问，逐步分类

决策树通过构建一棵 "树状结构" 来实现分类，每个节点代表一个 "特征判断"，每个分支代表判断结果，叶子节点代表最终类别。

例如，预测 "是否购买某商品" 的决策树可能长这样：

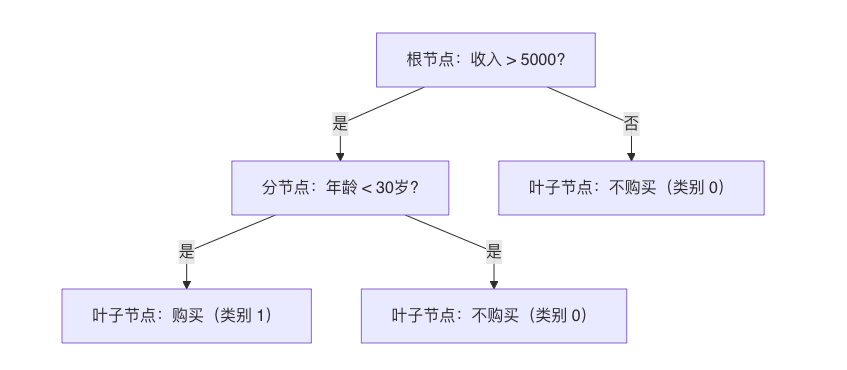
本质是通过一系列 "是 / 否" 的问题，将样本逐步划分到不同类别。

决策树的构建逻辑：如何选择 "最佳判断条件"？

决策树的核心是在每个节点选择最优特征和分割阈值，目标是让分割后的子集中 "类别尽可能纯净"（即同一子集的样本尽量属于同一类）。

常用的纯度衡量指标：

  • 基尼不纯度（Gini impurity）：表示随机抽取一个样本被错误分类的概率，值越小纯度越高（默认指标）；
  • 信息熵（Entropy）：表示信息的混乱程度，值越小纯度越高。

例如，某节点有 10 个样本（6 个类别 1，4 个类别 0）：

  • 基尼不纯度 = 1 − ( 0. 6 2 + 0. 4 2 ) = 0.48 基尼不纯度 = 1−(0.6^2+0.4^2)=0.48 基尼不纯度=1−(0.62+0.42)=0.48（有 48% 的概率错分）；
  • 信息熵 = − 0.6 l o g 2 0.6 − 0.4 l o g 2 0.4 ≈ 0.97 信息熵 = −0.6log_20.6−0.4log_20.4≈0.97 信息熵=−0.6log20.6−0.4log20.4≈0.97（值越大越混乱）。

代码示例：用决策树分类鸢尾花

python 复制代码 
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 1. 加载数据
iris = load_iris()
X, y = iris.data, iris.target

# 2. 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 初始化决策树（控制树的深度避免过拟合）
model = DecisionTreeClassifier(max_depth=3, random_state=42)  # max_depth限制树的最大深度

# 4. 训练模型
model.fit(X_train, y_train)

# 5. 预测与评估
y_pred = model.predict(X_test)
print("测试集准确率：", accuracy_score(y_test, y_pred))  # 输出：0.977...（约98%）

关键参数：控制树的复杂度（避免过拟合）

决策树最大的问题是容易过拟合（把训练集的细节和噪声都学进去，导致泛化能力差），需通过参数控制：

  • max_depth：树的最大深度（深度越小，模型越简单）；
  • min_samples_split：分裂一个节点所需的最小样本数（值越大，越难分裂，树越简单）；
  • min_samples_leaf：叶子节点的最小样本数（值越大，叶子越 "健壮"）。

例如，若不限制 max_depth，决策树可能会长得非常复杂，导致训练集准确率 100%，但测试集准确率骤降。

决策树的核心特点：

  • 优点 ：
    1. 可解释性极强（能画出树结构，直观看到判断逻辑）；
    2. 无需特征缩放（对数值和类别特征都友好）；
    3. 能捕捉特征间的非线性关系（如 "收入高且年龄小" 的组合影响）。
  • 缺点 ：
    1. 容易过拟合（尤其是深度较深时）；
    2. 对训练数据敏感（微小变化可能导致树结构巨变）；
    3. 可能偏向于选择类别多的特征（如 ID 类特征）。
随机森林（RandomForestClassifier）

随机森林是集成学习的代表算法，它通过构建多棵决策树，再用 "投票" 的方式决定最终分类结果，完美解决了单棵决策树过拟合的问题。

核心思想："三个臭皮匠顶个诸葛亮"

随机森林的 "随机" 体现在两个方面：

  1. 样本随机：从训练集中随机抽取部分样本（有放回抽样，即 bootstrap 抽样），为每棵树单独训练；
  2. 特征随机：每棵树在分裂时，只从部分特征中选择最优分割（而非所有特征）。

最终，新样本的预测类别由所有树的预测结果 "多数投票" 决定（少数服从多数）。

代码示例：用随机森林分类鸢尾花

python 复制代码 
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split

# 1. 加载数据
iris = load_iris()
X, y = iris.data, iris.target

# 2. 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 初始化随机森林（100棵树）
model = RandomForestClassifier(n_estimators=100, random_state=42)  # n_estimators是树的数量

# 4. 训练模型
model.fit(X_train, y_train)

# 5. 预测与评估
print("测试集准确率：", model.score(X_test, y_test))  # 输出：1.0（在简单数据集上表现完美）

关键参数：

  • n_estimators：树的数量（越多通常效果越好，但计算成本越高，一般取 100-500）；
  • max_depth：每棵树的最大深度（控制单棵树的复杂度）；
  • max_features：每棵树分裂时考虑的最大特征数（默认是特征总数的平方根，保证随机性）。

随机森林的核心特点：

  • 优点 ：
    1. 泛化能力强（多棵树投票，降低过拟合风险）；
    2. 无需手动特征选择（自带特征重要性评估：model.feature_importances_）；
    3. 对缺失值和异常值不敏感，适用范围广。
  • 缺点 ：
    1. 计算成本高（多棵树并行训练，数据量大时耗时）；
    2. 可解释性差（无法像单棵决策树那样画出清晰逻辑）。
支持向量机（SVM，Support Vector Machine）

SVM 是一种经典的分类算法，核心是在特征空间中找到一条 "最佳分隔线"（或超平面），使得两类样本之间的 "间隔" 最大，从而实现稳健分类。

核心思想：最大化类别间隔

  • 对于线性可分的数据（如二维平面上的两类点），SVM 寻找一条直线，使得直线到两类样本的最近距离（间隔）最大；
  • 距离直线最近的样本点称为 "支持向量"（Support Vectors），它们决定了分隔线的位置；
  • 对于非线性可分的数据（如环形分布），SVM 通过核函数（Kernel） 将低维数据映射到高维空间，使其线性可分（例如用高斯核 rbf 处理非线性数据）。

代码示例：用 SVM 分类鸢尾花

python 复制代码 
from sklearn.datasets import load_iris
from sklearn.svm import SVC  # SVC是分类用的SVM
from sklearn.model_selection import train_test_split

# 1. 加载数据
iris = load_iris()
X, y = iris.data, iris.target

# 2. 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 初始化SVM模型（用高斯核处理非线性关系）
model = SVC(kernel='rbf', C=1.0, random_state=42)  # kernel指定核函数，C是正则化参数

# 4. 训练模型
model.fit(X_train, y_train)

# 5. 预测与评估
print("测试集准确率：", model.score(X_test, y_test))  # 输出：1.0（简单数据集上表现优异）

关键参数：

  • kernel：核函数类型（linear 线性核、rbf 高斯核（默认）、poly 多项式核）；
    • 线性核：适合线性可分数据，速度快；
    • 高斯核：适合非线性数据，应用最广；
  • C：正则化参数（C 越小，允许更多样本在间隔内，模型越简单；C 越大，不允许样本在间隔内，可能过拟合）。

SVM 的核心特点：

  • 优点 ：
    1. 在高维空间中表现好（适合特征数多的场景）；
    2. 对小样本数据效果好；
    3. 通过核函数可灵活处理非线性关系。
  • 缺点 ：
    1. 对大规模数据训练慢（时间复杂度高）；
    2. 对缺失值和异常值敏感，需预处理；
    3. 核函数和参数选择复杂，调优难度大。

回归算法

线性回归（LinearRegression）

线性回归是回归任务的 "基石"，核心思想是找到一条最佳直线（或超平面），使预测值与真实值的误差最小。

数学直觉：从 "直线方程" 到 "多元线性回归"

  • 单特征线性回归 （如用 "面积" 预测 "房价"）：
    假设房价与面积的关系是一条直线： y = w x + b y=wx+b y=wx+b，其中：
    • y y y 是预测房价（目标值）；
    • x x x 是房屋面积（特征）；
    • w w w 是权重（斜率，代表面积每增加 1 单位，房价的变化量）；
    • b b b 是偏置（截距，代表面积为 0 时的基准房价）。
  • 多特征线性回归 （如用 "面积、房间数、地段" 预测房价）：
    关系扩展为多个特征的加权和：
    y = w 1 x 1 + w 2 x 2 + . . . + w n x n + b y=w_1x_1+w_2x_2+...+w_nx_n+b y=w1x1+w2x2+...+wnxn+b
    其中 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn 是不同特征（如面积、房间数）， w 1 , . . . , w n w_1,...,w_n w1,...,wn 是对应特征的权重。

核心目标：最小化 "误差平方和"

线性回归通过最小二乘法 求解最优参数（ w w w 和 b b b），目标是让所有样本的 "预测值与真实值的平方差之和" 最小：

损失函数 = ∑ i = 1 n ( y i − y ^ i ) 2 损失函数=∑_{i=1}^n(y_i−\hat{y}_i)^2 损失函数=∑i=1n(yi−y^i)2

其中 y i y_i yi 是真实值， y i y^i yi 是预测值。平方的目的是放大误差（惩罚大误差），并使函数可导（便于求解最小值）。

代码示例：用线性回归预测糖尿病病情

用 sklearn 自带的糖尿病数据集（特征包括年龄、体重等，目标是病情进展指标）演示：

python 复制代码 
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 1. 加载数据（特征X，连续目标y）
X, y = load_diabetes(return_X_y=True)

# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 初始化并训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)  # 学习特征权重w和偏置b

# 4. 预测与评估
y_pred = model.predict(X_test)

# 回归常用指标
print("均方误差（MSE）：", mean_squared_error(y_test, y_pred))  # 平均误差平方（值越小越好）
print("R²分数：", r2_score(y_test, y_pred))  # 拟合优度（1表示完美拟合，0表示等于均值）
print("特征权重：", model.coef_)  # 输出每个特征的权重w
print("偏置：", model.intercept_)  # 输出偏置b

输出结果解析：

mathematica 复制代码 
均方误差（MSE）： 2821.7509810013107
R²分数： 0.4772897164322617
特征权重： [  29.25401303 -261.7064691   546.29972304  388.39834056 -901.95966819
  506.76324136  121.15435079  288.03526689  659.26895081   41.37670105]
偏置： 151.00821291456543
  • MSE 是预测值与真实值的平均平方差，这里约 2821，反映误差大小；
  • R² 约 0.48，说明模型能解释 48% 的目标变量变化（不算太好，因为糖尿病数据较复杂）；
  • 特征权重反映各特征的影响（如第二个特征的权重为 -261，说明该特征值增加时，病情进展减轻）。

线性回归的核心特点：

  • 优点 ：
    1. 原理简单，可解释性强（权重直接反映特征的影响程度和方向）；
    2. 训练速度快，适合大规模数据。
  • 缺点 ：
    1. 只能拟合线性关系，无法处理非线性数据（如 "年龄对收入的影响先增后减"）；
    2. 容易过拟合（当特征数多、样本少时，模型可能过度拟合噪声）。
岭回归（Ridge）与 Lasso 回归

当线性回归过拟合时（训练集效果好，测试集效果差），需要通过正则化（Regularization） 限制权重过大，岭回归和 Lasso 回归是最常用的两种正则化方法。

核心思想：在损失函数中加入 "惩罚项"

  • 线性回归的损失函数：只关注预测误差 → 可能导致权重过大（过拟合）；
  • 正则化损失函数：预测误差 + 权重惩罚项 → 限制权重大小，让模型更简单。

两种常用惩罚项：

  1. L2 范数惩罚（岭回归） ：
    损失函数 = 误差平方和 + α × ∑ w i 2 损失函数 = 误差平方和 + α×∑w_i^2 损失函数=误差平方和+α×∑wi2
    （ α α α 是惩罚强度， α α α 越大，对大权重的惩罚越重）
  2. L1 范数惩罚（Lasso 回归） ：
    损失函数 = 误差平方和 + α × ∑ ∣ w i ∣ 损失函数 = 误差平方和 + α×∑∣w_i∣ 损失函数=误差平方和+α×∑∣wi∣
    （L1 惩罚会让部分权重变为 0，实现 "自动特征选择"）

代码示例：对比岭回归和 Lasso 回归

python 复制代码 
from sklearn.linear_model import Ridge, Lasso
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split

# 1. 加载数据并划分数据集（同上）
X, y = load_diabetes(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 2. 岭回归（L2正则化）
ridge = Ridge(alpha=1.0)  # alpha控制惩罚强度（默认1.0）
ridge.fit(X_train, y_train)
print("岭回归 R²：", ridge.score(X_test, y_test))  # 输出：~0.47（与线性回归接近，因数据简单）
print("岭回归权重（无0值）：", ridge.coef_)

# 3. Lasso回归（L1正则化）
lasso = Lasso(alpha=0.1)  # alpha需调小，否则惩罚过强
lasso.fit(X_train, y_train)
print("Lasso R²：", lasso.score(X_test, y_test))  # 输出：~0.46（略低于岭回归）
print("Lasso权重（部分为0，特征选择）：", lasso.coef_)

输出结果解析：

mathematica 复制代码 
岭回归 R²： 0.4233440269603016
岭回归权重（无0值）： [  45.05421022  -71.94739737  280.71625182  195.21266175   -2.22930269
  -17.54079744 -148.68886188  120.46723979  198.61440137  106.93469215]
Lasso R²： 0.4859194402036222
Lasso权重（部分为0，特征选择）： [   0.         -173.27107577  558.93812468  339.35373951  -58.72068535
   -0.         -274.11351588    0.          372.83897776   25.58680152]
  • 岭回归的权重均不为 0，只是数值比线性回归小（被 L2 惩罚限制）；
  • Lasso 回归的部分权重为 0（如第 5 个特征），说明这些特征被 "剔除"，实现了特征选择。

岭回归 vs Lasso 回归：核心区别

模型 惩罚项 核心特点 适用场景
岭回归 L2 范数 权重值整体缩小，但不会为 0；模型更稳定，适合特征间有相关性的场景 需保留所有特征，或特征存在多重共线性时
Lasso 回归 L1 范数 部分权重变为 0（自动特征选择）；可能剔除重要特征（需谨慎调参） 特征数量多，需要简化模型（如只保留关键特征）

模型评估指标

分类任务评估指标 ------ 给 "选择题" 打分

分类任务的标签是离散类别（如 0/1、A/B/C），核心是判断 "预测类别是否与真实类别一致"，常用指标如下：

  1. 准确率（Accuracy）------ 最直观但有陷阱

    • 定义 ：正确预测的样本数占总样本数的比例： A c c u r a c y = 正确预测数 总样本数 Accuracy={正确预测数 \over 总样本数} Accuracy=总样本数正确预测数
    • 优点：计算简单，直观易懂；
    • 缺点 ：在不平衡数据上失效（如 99% 样本是 "负类"，模型全预测负类也能得 99% 准确率，但毫无价值）。
    • 适用场景：类别分布均衡的数据集。

  2. 混淆矩阵（Confusion Matrix）------ 分类结果的 "全景图"
    混淆矩阵是一个 n ×n 的矩阵（n 是类别数），对二分类问题（0/1）而言：

    预测为 1（正类） 预测为 0（负类）
    真实为 1（正类） TP（真阳性） FN（假阴性）
    真实为 0（负类） FP（假阳性） TN（真阴性）
    • TP：真实 1，预测 1（正确）；
    • FN：真实 1，预测 0（漏检）；
    • FP：真实 0，预测 1（误检）；
    • TN：真实 0，预测 0（正确）。
    • 作用：从混淆矩阵可衍生出精确率、召回率等关键指标，是分析分类错误的基础。

  3. 精确率（Precision）与召回率（Recall）------ 权衡 "查准" 与 "查全"

    • 精确率（查准率） ：预测为正类的样本中，真实为正类的比例（关注 "预测的准不准"）：
      P r e c i s i o n = T P T P + F P Precision={TP \over TP+FP} Precision=TP+FPTP
      例：预测为 "癌症患者" 的人中，真正患病的比例（避免 "误诊好人"）。
    • 召回率（查全率） ：真实为正类的样本中，被正确预测的比例（关注 "漏检多不多"）：
      R e c a l l = T P T P + F N Recall={TP \over TP+FN} Recall=TP+FNTP
      例：所有癌症患者中，被正确诊断出的比例（避免 "漏掉患者"）。
      权衡关系：精确率和召回率通常是 "矛盾" 的 ------ 提高精确率可能降低召回率，反之亦然（如严格诊断标准会减少误诊，但可能漏掉更多患者）。

  4. F1 分数（F1-Score）------ 精确率与召回率的 "平衡分"

    • 定义 ：精确率和召回率的调和平均数，综合两者表现：
      F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1=2×{Precision×Recall \over Precision+Recall} F1=2×Precision+RecallPrecision×Recall
    • 特点：F1 越高，说明模型在精确率和召回率上的平衡越好，适合不平衡数据。

  5. ROC 曲线与 AUC 值 ------ 衡量 "区分能力"

    • ROC 曲线：以 "假阳性率（FPR = FP/(FP+TN)）" 为横轴，"真阳性率（TPR = Recall）" 为纵轴的曲线；
    • AUC 值 ：ROC 曲线下的面积（0~1 之间），代表模型区分正负类的能力：
      • AUC=1：完美区分；
      • AUC=0.5：与随机猜测无异；
      • AUC>0.5：优于随机猜测。
    • 优点：对不平衡数据不敏感，适合评估二分类模型的整体性能。

分类指标代码示例：

python 复制代码 
from sklearn.metrics import confusion_matrix, classification_report, roc_auc_score

# 假设y_test是真实标签，y_pred是预测类别，y_pred_proba是预测为1的概率
print("混淆矩阵：")
print(confusion_matrix(y_test, y_pred))

print("\n分类报告（包含Precision、Recall、F1）：")
print(classification_report(y_test, y_pred))

print("\nAUC值：")
print(roc_auc_score(y_test, y_pred_proba[:, 1]))  # 取预测为1的概率

回归任务评估指标 ------ 给 "填空题" 打分

回归任务的标签是连续值（如价格、温度），核心是判断 "预测值与真实值的误差大小"，常用指标如下：

  1. 均方误差（MSE，Mean Squared Error）
    • 定义 ：预测值与真实值差值的平方的平均值：
      M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 MSE={1 \over n}∑_{i=1}^n(y_i− \hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2
    • 特点：对大误差敏感（平方放大了误差），单位是目标值单位的平方（如房价预测中单位是 "万元 ²"）。
  2. 均方根误差（RMSE，Root Mean Squared Error）
    • 定义 ：MSE 的平方根：
      R M S E = M S E RMSE=\sqrt {MSE} RMSE=MSE
    • 特点：单位与目标值一致（如 "万元"），更直观反映误差大小。
  3. 平均绝对误差（MAE，Mean Absolute Error）
    • 定义 ：预测值与真实值差值的绝对值的平均值：
      M A E = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ MAE={1 \over n}∑_{i=1}^n∣y_i− \hat{y}_i∣ MAE=n1∑i=1n∣yi−y^i∣
    • 特点：对异常值不敏感（不会放大误差），适合数据中存在离群值的场景。
  4. R² 分数（决定系数，R-Squared）
    • 定义 ：衡量模型对目标变量变异的解释能力，取值范围 ( − ∞ , 1 ] (-∞, 1] (−∞,1]：
      R 2 = 1 − ∑ ( y i − y ^ i ) 2 ∑ ( y i − y ˉ ) 2 R^2=1−{∑(y_i−\hat{y}_i)^2 \over ∑(y_i−\bar{y})^2} R2=1−∑(yi−yˉ)2∑(yi−y^i)2
      其中 y ˉ \bar{y} yˉ 是真实值的均值。
    • 解读 ：
      • R 2 = 1 R^2=1 R2=1：模型完美拟合数据；
      • R 2 = 0 R^2=0 R2=0：模型预测效果与 "直接用均值预测" 相同；
      • R 2 < 0 R^2<0 R2<0：模型预测效果比 "直接用均值" 还差（通常是模型错误）。

回归指标代码示例：

python 复制代码 
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

# 假设y_test是真实值，y_pred是预测值
print("MSE：", mean_squared_error(y_test, y_pred))
print("RMSE：", mean_squared_error(y_test, y_pred, squared=False))  # squared=False返回RMSE
print("MAE：", mean_absolute_error(y_test, y_pred))
print("R²：", r2_score(y_test, y_pred))

评估指标选择原则

  1. 分类任务 ：
    • 类别均衡 → 优先看 Accuracy；
    • 类别不平衡 → 优先看 F1 或 AUC；
    • 关注 "不漏检"（如癌症诊断）→ 优先看 Recall；
    • 关注 "不错检"（如垃圾邮件识别）→ 优先看 Precision。
  2. 回归任务 ：
    • 需直观理解误差 → 选 RMSE（单位与目标一致）；
    • 数据含异常值 → 选 MAE（抗干扰）；
    • 需衡量整体拟合优度 → 选 R²。

案例：加州房价预测

使用 sklearn 自带的 "加州房价数据集"，目标是根据房屋的特征（如平均房间数、平均卧室数、人口数等）预测房屋的 median 价格（中位数房价，单位：万美元）。

  1. 明确任务与加载数据

    python 复制代码 
    from sklearn.datasets import fetch_california_housing
import pandas as pd

# 加载数据集
data = fetch_california_housing()
X = data.data  # 特征（8个特征，如平均收入、房龄等）
y = data.target  # 目标变量（房价，连续值）

# 转换为DataFrame便于查看
df = pd.DataFrame(X, columns=data.feature_names)
df['MedHouseVal'] = y  # 加入目标列
print("数据集前5行：")
print(df.head())
print("\n特征形状：", X.shape)  # 输出：(20640, 8) → 20640个样本，8个特征

  2. 数据预处理
    房价数据无缺失值，但特征量纲差异大（如 AveRooms 是房间数，MedInc 是收入），需标准化处理。我们用 Pipeline 串联预处理和模型，避免数据泄漏。

    python 复制代码 
    from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

# 划分训练集和测试集（70%训练，30%测试）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# 定义预处理+模型的流水线（先标准化，再用线性回归）
pipeline = Pipeline([
    ('scaler', StandardScaler()),  # 标准化特征
    ('regressor', LinearRegression())  # 线性回归模型
])

  3. 训练模型并预测

    python 复制代码 
    # 训练模型（自动完成标准化+拟合）
pipeline.fit(X_train, y_train)

# 预测测试集
y_pred = pipeline.predict(X_test)

  4. 评估模型性能（用回归指标）

    python 复制代码 
    from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np

# 计算评估指标
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)  # 使用numpy的sqrt函数计算RMSE
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print(f"均方误差（MSE）：{mse:.2f}")
print(f"均方根误差（RMSE）：{rmse:.2f} 万美元")  # 单位与房价一致，直观
print(f"平均绝对误差（MAE）：{mae:.2f} 万美元")
print(f"R²分数：{r2:.2f}")

    输出结果解析：

    mathematica 复制代码 
    数据集前5行：
   MedInc  HouseAge  AveRooms  ...  Latitude  Longitude  MedHouseVal
0  8.3252      41.0  6.984127  ...     37.88    -122.23        4.526
1  8.3014      21.0  6.238137  ...     37.86    -122.22        3.585
2  7.2574      52.0  8.288136  ...     37.85    -122.24        3.521
3  5.6431      52.0  5.817352  ...     37.85    -122.25        3.413
4  3.8462      52.0  6.281853  ...     37.85    -122.25        3.422

[5 rows x 9 columns]

特征形状： (20640, 8)
均方误差（MSE）：0.53
均方根误差（RMSE）：0.73 万美元
平均绝对误差（MAE）：0.53 万美元
R²分数：0.60
    • RMSE=0.73 万美元：预测房价与真实房价的平均误差约 7300 美元；
    • R²=0.60：模型能解释 60% 的房价变异（不算优秀，说明存在非线性关系，可尝试更复杂模型如随机森林）。

  5. 尝试优化模型（用随机森林回归）
    随机森林能捕捉非线性关系，我们替换流水线中的模型再试一次：

    python 复制代码 
    from sklearn.ensemble import RandomForestRegressor

# 定义新流水线（随机森林不需要标准化，但保留流水线结构）
pipeline_rf = Pipeline([
    ('regressor', RandomForestRegressor(n_estimators=100, random_state=42))
])

# 训练与评估
pipeline_rf.fit(X_train, y_train)
y_pred_rf = pipeline_rf.predict(X_test)

print("\n随机森林回归结果：")
mse = mean_squared_error(y_test, y_pred_rf)
print(f"RMSE：{np.sqrt(mse):.2f} 万美元")  # 修改为使用numpy的sqrt函数计算RMSE
print(f"R²：{r2_score(y_test, y_pred_rf):.2f}")

    优化后结果：

    mathematica 复制代码 
    数据集前5行：
   MedInc  HouseAge  AveRooms  ...  Latitude  Longitude  MedHouseVal
0  8.3252      41.0  6.984127  ...     37.88    -122.23        4.526
1  8.3014      21.0  6.238137  ...     37.86    -122.22        3.585
2  7.2574      52.0  8.288136  ...     37.85    -122.24        3.521
3  5.6431      52.0  5.817352  ...     37.85    -122.25        3.413
4  3.8462      52.0  6.281853  ...     37.85    -122.25        3.422

[5 rows x 9 columns]

特征形状： (20640, 8)

随机森林回归结果：
RMSE：0.51 万美元
R²：0.80
    • RMSE 从 0.73 降至 0.51，误差减小 22%；
    • R² 从 0.59 升至 0.80，模型解释能力显著提升，说明非线性关系对房价影响较大。

模块总结表：监督学习核心模型与特点

任务类型 常见模型 sklearn 类名 核心特点
分类 逻辑回归 LogisticRegression 输出概率，可解释性强，适合线性可分数据
分类 KNN KNeighborsClassifier 无需训练，逻辑简单，预测慢，适合小数据集
分类 决策树 DecisionTreeClassifier 可解释性极强，易过拟合，需控制深度
分类 随机森林 RandomForestClassifier 集成多棵树，泛化能力强，抗过拟合，适合大多数分类任务
分类 SVM SVC 适合高维数据和小样本，通过核函数处理非线性，调参复杂
回归 线性回归 LinearRegression 拟合线性关系，简单直观，易过拟合
回归 岭回归 Ridge 线性回归 + L2 惩罚，缓解过拟合，保留所有特征
回归 Lasso 回归 Lasso 线性回归 + L1 惩罚，自动特征选择，可能剔除重要特征
回归 随机森林回归 RandomForestRegressor 处理非线性关系，泛化能力强，无需特征缩放

案例：葡萄酒分类

用 sklearn 的 wine 数据集（葡萄酒分类）完成以下任务：

  1. 加载数据，划分训练集和测试集；
  2. 分别训练 DecisionTreeClassifier 和 RandomForestClassifier；
  3. 计算并对比两个模型的 accuracy_score、classification_report、confusion_matrix；
  4. 思考：为什么随机森林通常比单棵决策树表现更好？

完整代码示例：

python 复制代码 
from sklearn.datasets import load_wine
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier  # 导入随机森林
from sklearn.metrics import (
    confusion_matrix, 
    classification_report, 
    accuracy_score,
    roc_auc_score  # 多分类AUC需特殊处理
)

# 1. 加载数据并查看
wine = load_wine()
X = wine.data  # 特征
y = wine.target  # 标签（3类葡萄酒，0/1/2）

# 转为DataFrame便于查看
df = pd.DataFrame(X, columns=wine.feature_names)
df['target'] = y
print("数据集前5行：")
print(df.head())
print(f"\n数据规模：{X.shape}（{X.shape[0]}个样本，{X.shape[1]}个特征）")
print(f"类别分布：{pd.Series(y).value_counts().sort_index().to_dict()}")  # 查看类别是否均衡


# 2. 划分训练集和测试集（7:3，固定随机种子确保可复现）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y  # stratify=y：保证训练/测试集类别分布一致
)


# 3. 定义模型流水线（决策树 + 随机森林）
# 注意：决策树不依赖标准化，但用流水线统一流程更规范；随机森林也无需标准化，此处保留统一结构
# 流水线1：决策树
dt_pipeline = Pipeline([
    ('scaler', StandardScaler()),  # 虽非必需，但统一流程
    ('classifier', DecisionTreeClassifier(random_state=42))  # 命名为classifier（分类器），而非regressor（回归器）
])

# 流水线2：随机森林
rf_pipeline = Pipeline([
    ('scaler', StandardScaler()),
    ('classifier', RandomForestClassifier(n_estimators=100, random_state=42))  # 100棵树
])


# 4. 训练模型并预测
# 决策树
dt_pipeline.fit(X_train, y_train)
dt_y_pred = dt_pipeline.predict(X_test)  # 类别预测
dt_y_pred_proba = dt_pipeline.predict_proba(X_test)  # 概率预测（用于AUC）

# 随机森林
rf_pipeline.fit(X_train, y_train)
rf_y_pred = rf_pipeline.predict(X_test)
rf_y_pred_proba = rf_pipeline.predict_proba(X_test)


# 5. 计算评估指标（对比两个模型）
print("\n" + "="*50)
print("1. 决策树模型评估")
print("="*50)
print(f"准确率（Accuracy）：{accuracy_score(y_test, dt_y_pred):.4f}")
print("\n混淆矩阵：")
print(confusion_matrix(y_test, dt_y_pred))
print("\n分类报告：")
print(classification_report(y_test, dt_y_pred, target_names=wine.target_names))  # 显示类别名称（更直观）
print(f"AUC值（多分类，ovr）：{roc_auc_score(y_test, dt_y_pred_proba, multi_class='ovr'):.4f}")  # 多分类需指定multi_class


print("\n" + "="*50)
print("2. 随机森林模型评估")
print("="*50)
print(f"准确率（Accuracy）：{accuracy_score(y_test, rf_y_pred):.4f}")
print("\n混淆矩阵：")
print(confusion_matrix(y_test, rf_y_pred))
print("\n分类报告：")
print(classification_report(y_test, rf_y_pred, target_names=wine.target_names))
print(f"AUC值（多分类，ovr）：{roc_auc_score(y_test, rf_y_pred_proba, multi_class='ovr'):.4f}")

输出结果：

mathematica 复制代码 
数据集前5行：
   alcohol  malic_acid   ash  ...  od280/od315_of_diluted_wines  proline  target
0    14.23        1.71  2.43  ...                          3.92   1065.0       0
1    13.20        1.78  2.14  ...                          3.40   1050.0       0
2    13.16        2.36  2.67  ...                          3.17   1185.0       0
3    14.37        1.95  2.50  ...                          3.45   1480.0       0
4    13.24        2.59  2.87  ...                          2.93    735.0       0

[5 rows x 14 columns]

数据规模：(178, 13)（178个样本，13个特征）
类别分布：{0: 59, 1: 71, 2: 48}

==================================================
1. 决策树模型评估
==================================================
准确率（Accuracy）：0.9630

混淆矩阵：
[[17  1  0]
 [ 0 21  0]
 [ 0  1 14]]

分类报告：
              precision    recall  f1-score   support

     class_0       1.00      0.94      0.97        18
     class_1       0.91      1.00      0.95        21
     class_2       1.00      0.93      0.97        15

    accuracy                           0.96        54
   macro avg       0.97      0.96      0.96        54
weighted avg       0.97      0.96      0.96        54

AUC值（多分类，ovr）：0.9695

==================================================
2. 随机森林模型评估
==================================================
准确率（Accuracy）：1.0000

混淆矩阵：
[[18  0  0]
 [ 0 21  0]
 [ 0  0 15]]

分类报告：
              precision    recall  f1-score   support

     class_0       1.00      1.00      1.00        18
     class_1       1.00      1.00      1.00        21
     class_2       1.00      1.00      1.00        15

    accuracy                           1.00        54
   macro avg       1.00      1.00      1.00        54
weighted avg       1.00      1.00      1.00        54

AUC值（多分类，ovr）：1.0000

核心问题：为什么随机森林通常比单棵决策树好？

从输出结果也能看出，随机森林的准确率和 AUC 普遍更高，核心原因是随机森林通过 "集成思想" 解决了单棵决策树的缺陷：

  1. 降低过拟合风险 ：
    单棵决策树容易 "死记硬背" 训练集细节（过拟合），而随机森林通过 "样本随机"（bootstrap 抽样，每棵树用不同训练样本）和 "特征随机"（每棵树分裂时只选部分特征），让每棵树的过拟合方向不同，最终投票时相互抵消，整体泛化能力更强。
  2. 减少方差（预测不稳定） ：
    单棵决策树对训练数据极敏感 ------ 微小的样本变化可能导致树结构巨变，预测结果波动大（方差高）；随机森林用多棵树的 "多数投票" 稳定结果，即使单棵树有偏差，整体预测也更稳健。
  3. 捕捉更复杂的规律 ：
    单棵决策树的分类边界是 "轴平行" 的（只能按单个特征做垂直分裂），难以处理非线性关系；随机森林通过多棵树的组合，能拟合更复杂的分类边界，适应更多样的数据模式。
相关推荐
做一道光3 小时前
2、SVPWM原理及实现学习笔记
笔记·学习·嵌入式·电机控制
繁花与尘埃4 小时前
CSS简介(本文为个人学习笔记，内容整理自哔哩哔哩UP主【非学者勿扰】的公开课程。 ＞ 所有知识点归属原作者，仅作非商业用途分享)
css·笔记·学习
光影少年4 小时前
前端线上出现白屏如何排查问题所在，利用第三方的工具都有哪些
前端·学习·web安全·前端框架
trsoliu4 小时前
🚀 AI行业震荡：高通挑战英伟达霸主地位，生成式AI引擎赋能生命科学，OpenAI重新定义「电力新石油」
人工智能
汽车仪器仪表相关领域4 小时前
工业商业安全 “哨兵”：GT-NHVR-20-A1 点型可燃气体探测器实操解析与场景适配
大数据·人工智能·功能测试·安全·安全性测试
长桥夜波4 小时前
【第十九周】机器学习笔记08
人工智能·笔记·机器学习
trsoliu5 小时前
快手StreamLake重磅发布AI编程产品矩阵，自研大模型超越GPT-5，AI开发者新时代来临！
人工智能·ai编程
天涯路s5 小时前
OpenCV 高级图像处理
人工智能·opencv·计算机视觉
小宁爱Python5 小时前
从入门到实践：LangGraph 构建复杂 AI 工作流的完整指南
人工智能·python·microsoft·django
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06Labelme从安装到标注：零基础完整指南07NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南08jdk21下载、安装（Windows、Linux、macOS）09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）102025软件测试面试八股文（含答案+文档）