pytorch若干重要函数与重要理论的学习和实践
前言:最近面试被多次拷打torch,numpy等库基础函数,于是决定整理学习相关函数。在网上发现了这个网站,十分推荐。
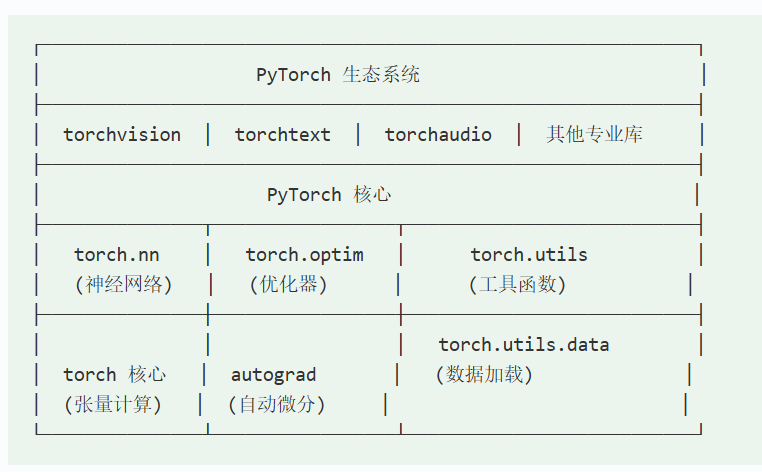
pytorch的架构图如上,其核心操作有torch.nn神经网络,torch.optim优化器,torch.utils工具函数,torch核心,autograd自动微分,torch.utils.data数据加载。
一.张量tensor若干操作
简单操作
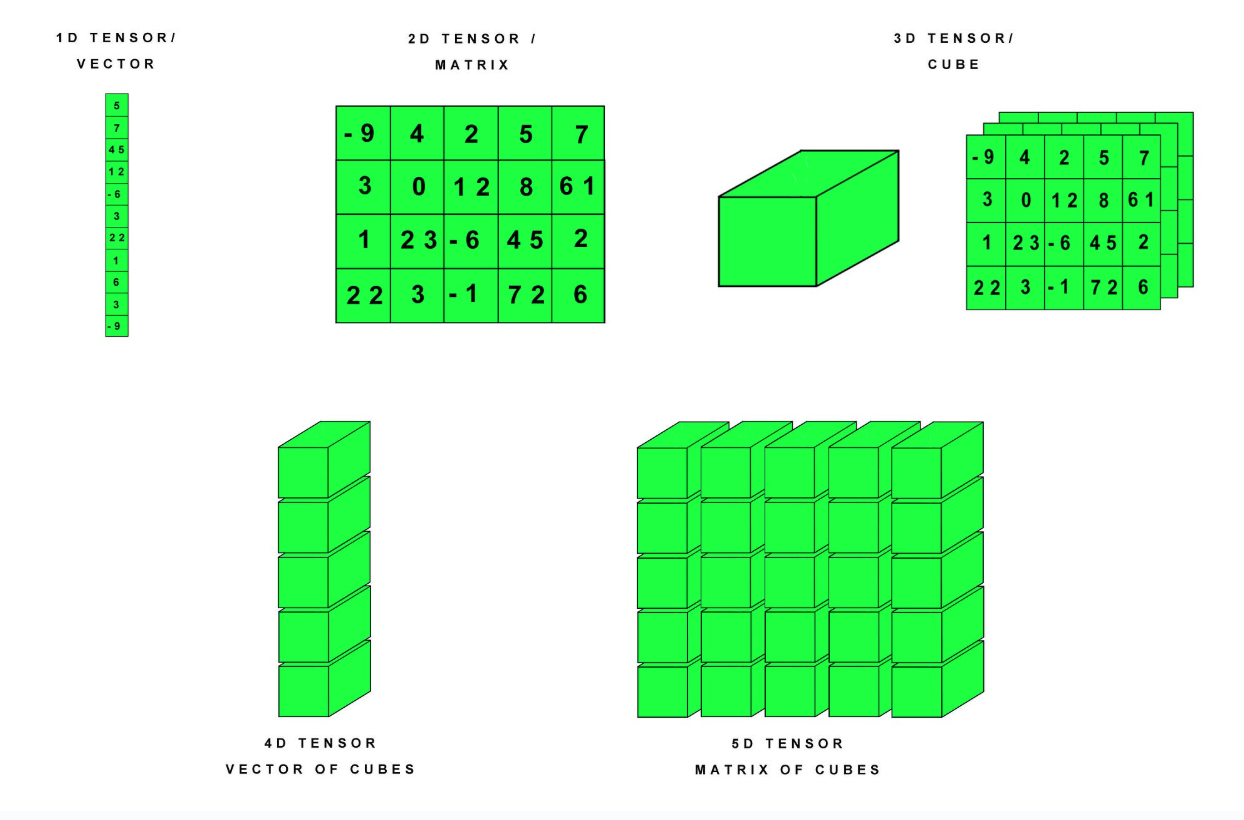
在下图中展示了不同维度的张量在pytorch中的存储方法
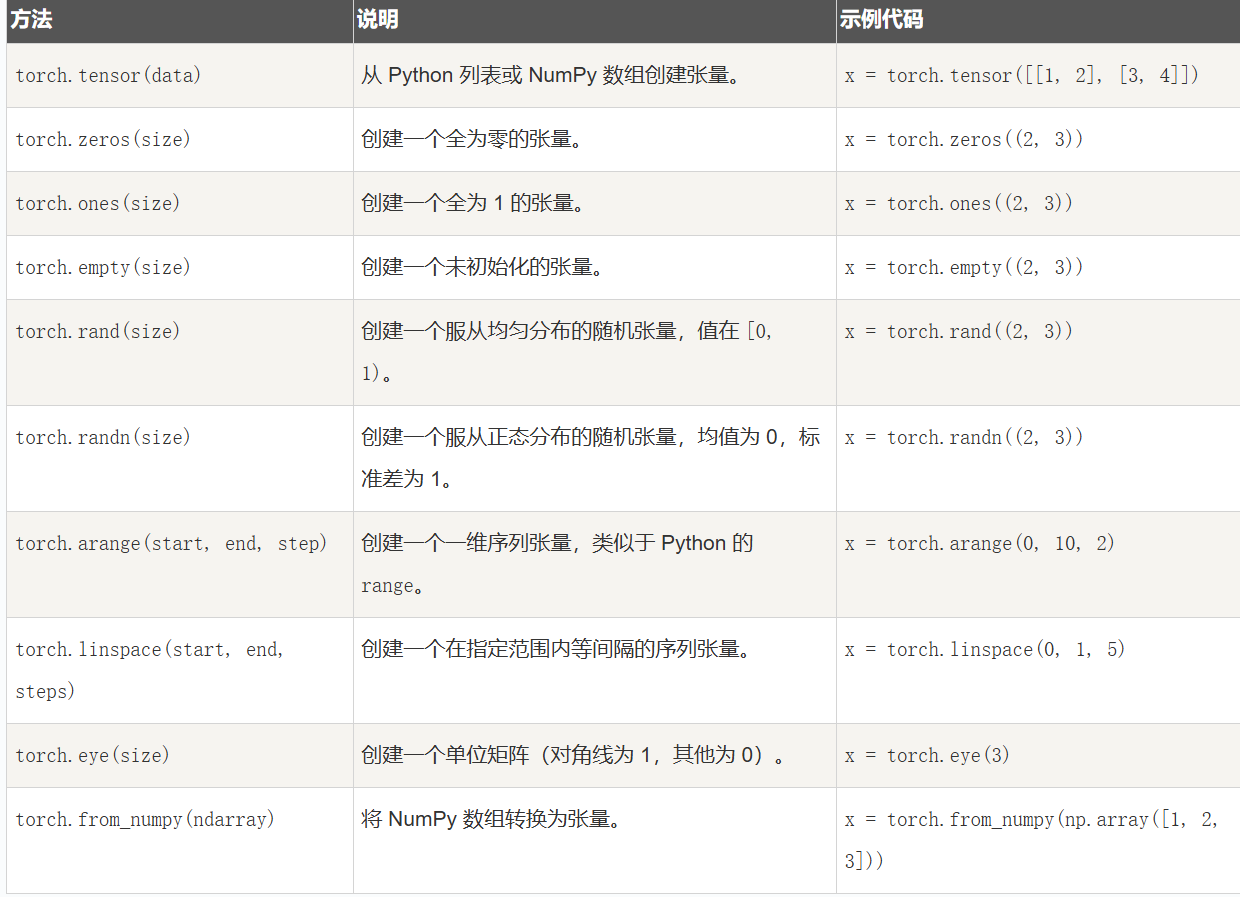
在pytorch中张量创建的方法有:
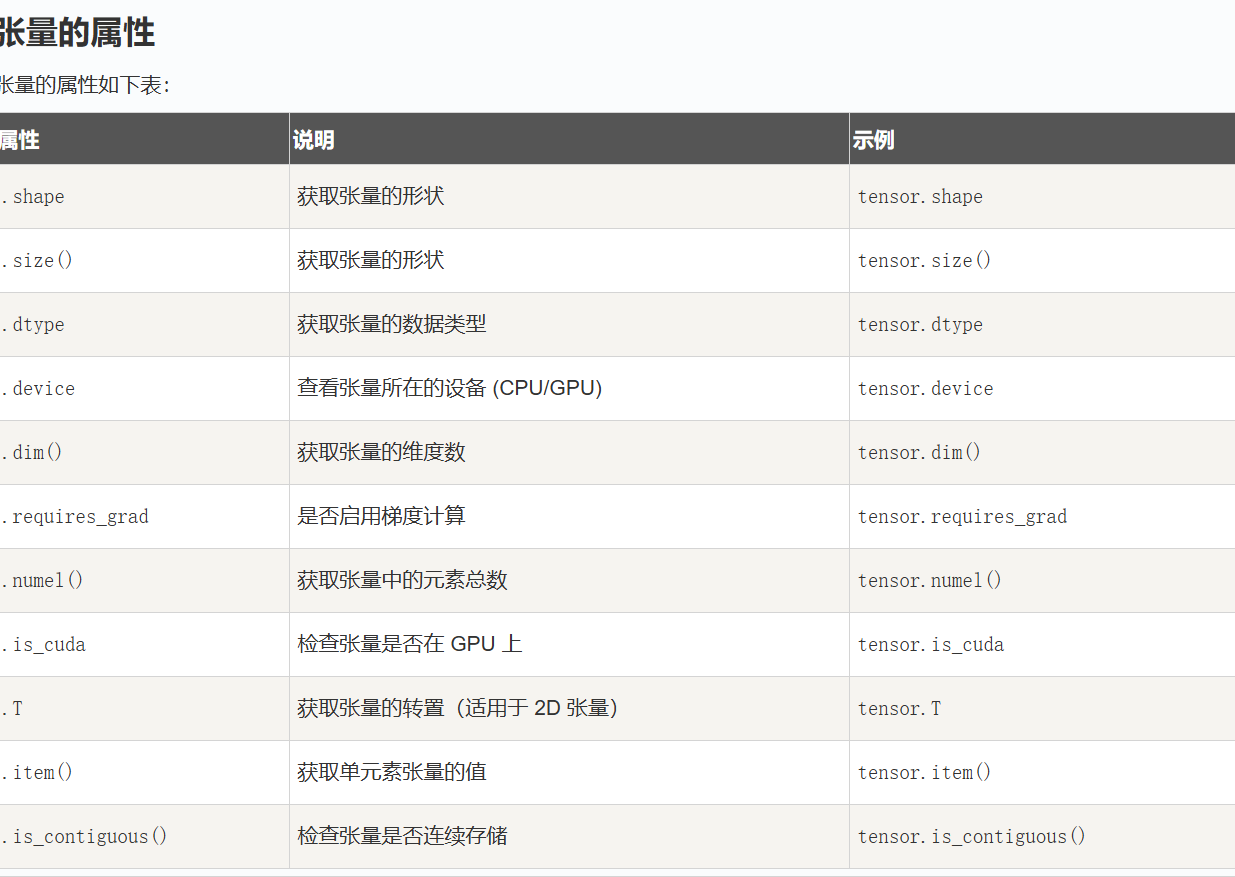
张量的属性如下表。常用的有tensor.shape获取张量的形状,tensor.size()获取张量的形状,tensor.dtype获取张量的数据类型,torch.device查看张量所存在的设备。
python
import torch
print("tensor\n",tensor)
print("shape:",tensor.shape)
print("size",tensor.size())#打印大小
print("data type",tensor.dtype)#打印数据类型
print("dimension",tensor.dim())#打印tensor维度
print("total elements",tensor.numel)#打印全部元素
print("requires grad",tensor.requires_grad)
print("is on CUDA",tensor.is_cuda)#打印是否存在GPU上
single_value=torch.tensor(42)#单元素的张量
print("single element value",single_value.item())
对于tensor 张量的维度,应当注意torch.tensor([[1,2,3],[4,5,6]])的形状是torch.Size([2,3])因为在dim=0时候有两个元素,dim=1的时候有三个元素,常见的判断一般都是二维的。
矩阵的运算
python
tensor1=torch.tensor([[1,2,3],
[4,5,6]],requires_grad=True,dtype=torch.float32)#简单的二维矩阵
print("第一行",tensor1[0])
print("第一行第一列",tensor1[0,0])
print("第二列所有元素",tensor1[:,1])
#下面是常用的view函数,是形状变化的函数,用法系:
tensor2=tensor1.view(2,3)#由3,2变为2,3
flattened=tensor1.flatten()#把张量铺平为一维的
print("viewed",tensor2)
print("flattened",flattened)
tensor_add=tensor2.add(10)
tensor_mul=tensor_add*2
tensor_sum=tensor.sum()#对张量的所有元素相加
print("tensor add",tensor_add)
print("tensor mul",tensor_mul)
print("tensor all sum",tensor_sum.item())
#下面是与其他的张量操作
tensor3=torch.tensor([[1,2,3],[4,5,6]],requires_grad=True,dtype=torch.float32)
tensor_dot=torch.matmul(tensor2,tensor3.T)#按照矩阵知识,相乘的话前一个矩阵的行数应该和后一个矩阵的列数相等
print("tensor dot",tensor_dot)
#下面再实现让矩阵的相乘发生在gpu上面
if torch.cuda.is_available():
device = torch.device("cuda") # 使用默认 GPU
print(f"Using GPU: {torch.cuda.get_device_name(0)}")
else:
device = torch.device("cpu")
print("No GPU available, using CPU.")
A = torch.randn(3, 4) # 3x4 矩阵
B = torch.randn(4, 5) # 4x5 矩阵
# 将矩阵移动到 GPU
A_gpu = A.to(device) # 方法1:推荐,灵活支持 CPU/GPU
B_gpu = B.cuda() # 方法2:等效,但硬编码为 CUDA
tensor_out=torch.matmul(A_gpu,B_gpu)#即matrix multiply
print("gpu based tensor_out",tensor_out)
#下面是对张量进行条件判断的操作:
mask=tensor1>3#创建一个bool掩码
filter_ed=tensor1[mask]
print("大于3的元素",filter_ed)和matlab中的矩阵运算有些相似,矩阵加法和乘法分为矩阵和单个元素的运算和矩阵与矩阵的运算,tensor.add()是相加,torch.matmul()是张量相乘。想要把tensor从cpu内存移动到GPU中,要用tensor.to(device),或者tensor.cuda()在gpu上进行张量运算远比在cpu上更快。因为从底层的数字集成电路上,GPU就是为张量运算设计的。
运行后输出结果为:
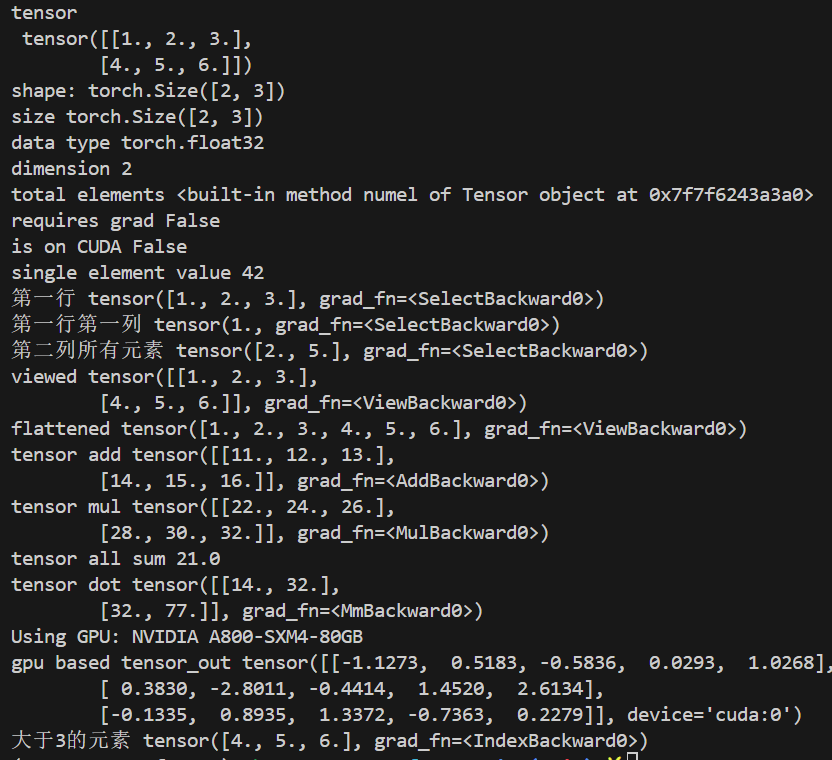
tensor与numpy array间的相互转化
tensor与numpy可以相互转换,常见的tensor 转换为Numpy的方法有独立的:tensor.clone().numpy()和非独立的tensor.numpy()。
而把numpy array转化为tensor的方法如下:torch.from_numpy(numpy),相应的代码示例为:
python
import torch
import numpy as np
tensor1=torch.tensor([[1,2,3],[4,5,6]],dtype=torch.float16)
num_array=np.array([[1,2,3],[4,5,6]])
tensor_from_numpy=torch.from_numpy(num_array)
print("转换后的张量",tensor_from_numpy)
num_array[0,0]=100#对numpy数组进行修改
tensor_change=tensor1.numpy()
print("转化后的numpy数组",tensor_change)
#在不共享内存的情况下需要先clone再转化为numpy格式,此时修改tensor数据后,numpy的数据不会改变
numpy_indepent=tensor1.clone().numpy()
tensor1[0,0]=10
print("numpy after tensor changed(independent)",numpy_indepent)二.detach函数
在pytorch中数据存储为张量形式,每个张量都是计算图上的一个节点,它们通过一系列操作相互连接。这些操作不仅定义了张量之间的关系,还构建了用于梯度传播的计算历史。梯度传播是深度学习模型训练的核心,它允许我们通过反向传播算法计算损失函数对模型参数的梯度,进而优化模型。
在某些情况下,需要从计算图中分离出一些张量来避免不必要的梯度张量计算。在某些场景中,分离张量非常实用 。例如,在模型推理阶段,我们往往不需要计算梯度,因此可以通过detach()来降低内存消耗并提升计算效率。此外,当你想要获取一个张量的值,但又不想让这个值参与到后续的计算图中时,detach()函数也是你的理想选择。
detach()函数是从原来的张量中分离出一个新的张量而不会改变原始张量的属性。
python
import torch
x=torch.tensor([2.0],requires_grad=True)#说明x张量需要梯度
y=x*2
print(y.requires_grad)#输出为True
print("\n")
y_detached=y.detach()#从计算图中分离出y,不需要计算梯度
print(y_detached.requires_grad)#输出为False三.torch.nn.linear线性神经网络函数
python3
torch.nn.Linear(in_features, # 输入的神经元个数
out_features, # 输出神经元个数
bias=True # 是否包含偏置
)在数学上讲,nn其实就是简单的线性+偏置变换。
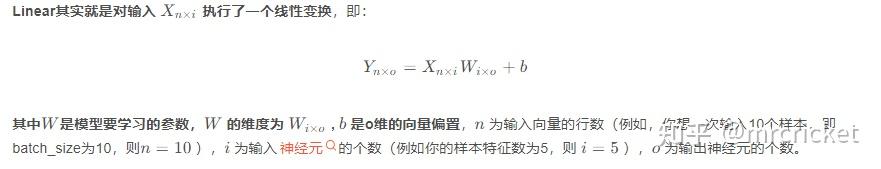
python
import torch.optim as optim
import torch
import torch.nn as nn
class simpleNN(nn.Module):
def __init__(self,input_size,hidden_size,output_size):
super(simpleNN,self).__init__()#获取simpleNN父类的构造函数并进行构造
self.fc1=nn.Linear(input_size,hidden_size)#第一层
self.fc2=nn.Linear(hidden_size,output_size)#第二层
def forward(self,x):#前向传播算法
x=torch.relu(self.fc1(x))#首先是激活函数
x=self.fc2(x)
return x #前向传播函数必须有返回值
model=simpleNN(input_size=10,hidden_size=5,output_size=1)
input_data=torch.randn(1,10,requires_grad=True)#torch. randn函数生成的是标准差为1的矩阵
output=model(input_data)#前向传播
loss=(output - torch.tensor([1.0]))**2#其实就是简单的MSE
optimizer = optim.SGD(model.parameters(), lr=0.01) # lr 是学习率
loss.backward()#torch自动计算Loss关于所有权重的梯度,告诉模型该怎么优化
optimizer.step()#模型自动改进
optimizer.zero_grad()#清空梯度
detached_input=input_data.detach()
print(output)#打印输出
print(detached_input.requires_grad)#打印detached后的输出
detached_out=model(detached_input)#
detached_loss=(detached_out-torch.tensor([1.0]))**2
detached_loss.backward()
print(detached_input.requires_grad)
print(detached_input.grad)#打印detached input的grad,由于其被detach故没有grad这段代码通过使用nn.linear()函数和基于torch.nn.Module父类构造了简单的神经网络模型simpleNN并测试了前向传播和反向传播。并且发现如果用了detach()函数,那么打印出来的detached_input.grad就算None.其中用到的backward()是常用的损失反向传播函数,即计算loss关于所有权重的梯度。
四.nn.sequential函数和基于torch的简单训练过程
nn.Sequential是一个容器模块,用于按照顺序组合多个神经网络层(如卷积层、激活函数、池化层)。nn.Sequential可以允许将多个模块封装成一个模块,forward函数接收输入之后,nn.Sequential按照内部模块的顺序自动依次计算并输出结果。nn.Sequential内部实现了forward函数,因此可以不用写forward函数。写nn.Sequential函数可以简单的构造一个神经网络。
python
import torch
import torch.nn as nn
import torch.optim as optim
model=nn.Sequential(#通过sequential把线性层,激活层等连起来就是个能用的模块
nn.Linear(10,5),
nn.ReLU(),#激活函数,用于决定神经元是否该被激活,其是非线性函数
nn.Linear(5,1)
)
optimzer=optim.SGD(model.parameters(),lr=0.001)#SGD是随机梯度动量下降
cirterion=nn.MSELoss()#均方误差损失
inputs=torch.randn(100,10,requires_grad=True)#100个输入值,随机的
targets=torch.randn(100,1)#100个目标值,也是随机的,randn 是random normalized
for epoch in range(50):#一共设置五十个epoch,每个epoch都把样本喂进去一遍
epoch_loss=0.0
for i in range(100):
optimzer.zero_grad()#清空积累的grad
output=model(inputs[i].unsqueeze(0))#前向传播,squeeze函数是挤压函数是删除某某维度,unsequeeze函数是增加恢复维度,把输入数据添加batch维度
loss=cirterion(output,targets[i].unsqueeze(0))#loss直接调用现成的MSE
loss.backward()#反向传播,如果不加上反向传播的话后续step就算无效的
optimzer.step()#step()函数根据反向传播调整
epoch_loss+=loss.item()#epoch loss是每个样本的loss相加起来
print(f"Epoch{epoch+1},loss:{epoch_loss/100:.4f}")对于简单训练过程,首先用sequential定义了个模型,再用optim.SGD随机梯度动量下降定义了个优化器,随后在epoch遍历中每次调用model前向传播获得output再用nn.MSELoss()作为损失函数,先对loss作backward操作,再调用optimzer.step()函数推进优化器迭代,如此循环即可。
五.pytorch中的加载文本数据和图像数据的函数
在pytorch中为了高效的去处理数据,提供了torch.utils.data.Dataset和torch.utils.data.DataLoader这两个工具。torch.utils.data.Dataset和torch.utils.data.DataLoader是配套的,一个制作数据集一个加载数据集。
示例代码如下:在下面的代码中首先在基类Dataset的基础上建了个简单的x->y数据集。随后再用dataloader调用并指定batch打印。
python
import torch
from torch.utils.data.dataset import Dataset
from torch.utils.data.dataloader import DataLoader
class MyDataset(Dataset):
def __init__(self,X_data,Y_data):
self.x_data=X_data
self.y_data=Y_data
def __len__(self):
return len(self.x_data)#获得数据集的大小
def __getitem__(self,idx):
x=torch.tensor(self.x_data[idx],dtype=torch.float32)#定义x并对其张量化
y=torch.tensor(self.y_data[idx],dtype=torch.float32)
return x,y
X_data = [[1, 2], [3, 4], [5, 6], [7, 8],[9,10],[11,12]] # 输入特征
Y_data = [1, 0, 1, 0,0,0] # 目标标签
dataset=MyDataset(X_data,Y_data)
dataloader=DataLoader(dataset,batch_size=2,shuffle=True)
for epoch in range(1):
for batch_idx,(inputs,labels) in enumerate(dataloader):#enumeate用于在遍历序列的同时获得元素的索引和值
print(f"Batch{batch_idx+1}")
print(f"Inputs:{inputs}")
print(f"labels:{labels}")其中的dataloader=DataLoader(dataset,batch_size=2,shuffle=True)中的shuffle是打乱的意思。分batch_size=2是意思把数据集分为batch size为2的若干个数据batch。而enumerate函数的作用是可以遍历序列的同时获得元素和索引值。
加载图像数据集下面放在和卷积神经网络部分一起做,整个最简单的图像识别的demo。
六.nn.conv2d与pytorch实现卷积神经网络
pytorch卷积神经网络是一类专门用于处理具有网格状拓扑结构数据(如图像)的深度学习模型。
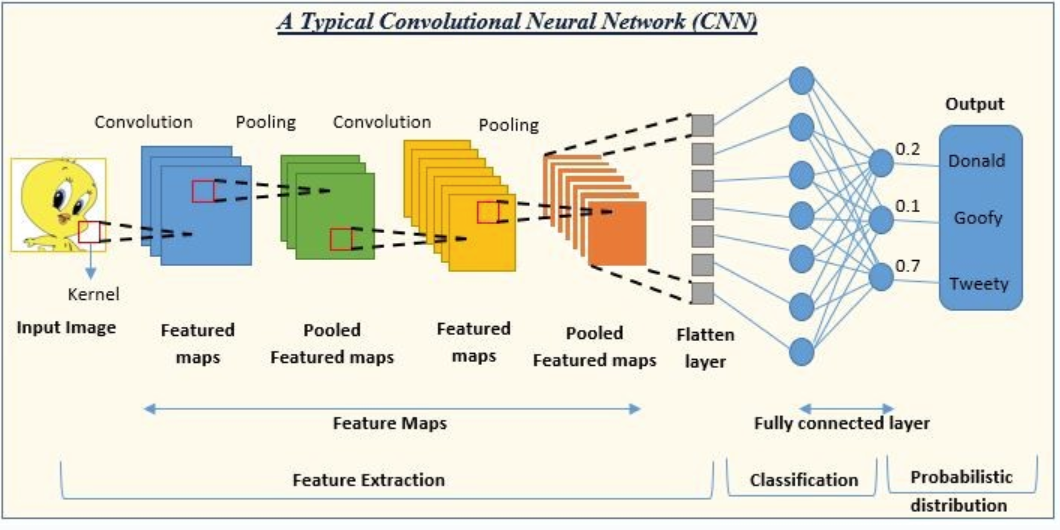
正如该图所示,展示了卷积神经网络的流程,其中的卷积是通过卷积核kernel在图像上滚动来提取特征生成特征图。而池化层pooling跟在卷积层后面的目的是通过最大池化或平均池化减少特征图的尺寸,同时保留重要特征,生成池化特征图(Pooled Feature Maps)。最终的Flatten layer展平层目的是将多维的特征图转换为一维向量,以便输入到全连接层。最终的全连接层则类似于传统的神经网络层,用于将提取的特征映射到输出类别。输出最后的probablity再根据排序即可知道卡通图像对应的角色。

python
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
import torch.optim as optim
#首先需要定义一个卷积神经网络
transform = transforms.Compose([
transforms.ToTensor(), # 转为张量
transforms.Normalize((0.5,), (0.5,)) # 归一化到 [-1, 1]
])
# 加载 MNIST 数据集,MNIST即经典的数字识别数据集有数万个手写数字样本按照9比1分为训练和测试
train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True)
test_dataset = datasets.MNIST(root='./data', train=False, transform=transform, download=True)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=64, shuffle=False)
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN,self).__init__()#父类初始化
self.conv1=nn.Conv2d(1,32,kernel_size=3,stride=1,padding=1)#这里的参数kernel_size是卷积核大小,stride是滑动步长,padding是填充
#1是输入通道为1,单通道即灰度图像,如果输入是3,则为RGB图像
#输出32是特征数量
self.pool1 = nn.MaxPool2d(2, 2) # 池化层!,向下采样,降低特征图的尺寸,第一个参数为kernel_size,第二个是stride,两者均为2意思是特征图直接降为一遍
#另外还有计算公式:输出高度 = (输入高度 + 2×padding - kernel_size) / stride + 1,输出宽度 = (输入宽度 + 2×padding - kernel_size) / stride + 1
self.conv2=nn.Conv2d(32,64,kernel_size=3,stride=1,padding=1)#定义第二个卷积层
self.pool2 = nn.MaxPool2d(2, 2) # 池化层!
#下面定义全连接层
self.fc1=nn.Linear(64*7*7,128)#输入大小为特征图大小*通道数
#这里写64*7*7是因为前面经过了两个池化层,原来的28像素变成了28/2/2为7,当然了这个28是因为MNIST数据集分辨率很低。
self.fc2=nn.Linear(128,10)#输出最终为10个类别即数字预测从0到9
self.dropout=nn.Dropout(0.5)#防止过拟合
def forward(self,x):#前向传播函数
x=self.pool1(torch.relu(self.conv1(x)))#先经过卷积层再过激活层再过池化层
x=self.pool2(torch.relu(self.conv2(x)))#先经过卷积层再过激活层再过池化层
x=x.view(-1,64*7*7)#展平
x=torch.relu(self.fc1(x))#过第一个全连接层
x=self.dropout(x)#防止过拟合层
x=self.fc2(x)#第二个全连接层
return x
device=torch.device("cuda" if torch.cuda.is_available() else "cpu")
model=SimpleCNN().to(device)#如果model移动到gpu上,那么后面的images和labels也该移动到gpu上
criterion=nn.CrossEntropyLoss()#交叉熵损失函数
optimizer=optim.Adam(model.parameters(),lr=0.001)#Adam是自适应学习率的优化算法
num_epochs = 5
model.train() # 设置模型为训练模式
for epoch in range(num_epochs):
total_loss = 0
for images, labels in train_loader:
images=images.to(device)
labels=labels.to(device)
outputs = model(images) # 前向传播
loss = criterion(outputs, labels) # 计算损失
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 更新参数
total_loss += loss.item()#total_loss是每个image和label的loss的和
print(f"Epoch [{epoch+1}/{num_epochs}], Loss: {total_loss / len(train_loader):.4f}")
model.eval() # 设置模型为评估模式
correct = 0
total = 0
with torch.no_grad(): # 关闭梯度计算
for images, labels in test_loader:
images=images.to(device)
labels=labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
accuracy = 100 * correct / total
print(f"Test Accuracy: {accuracy:.2f}%")借助nn.conv2d等函数实现神经网络搭建到训练和测试的代码如上所示:运行结果如下:

七.pytorch 实现transformer
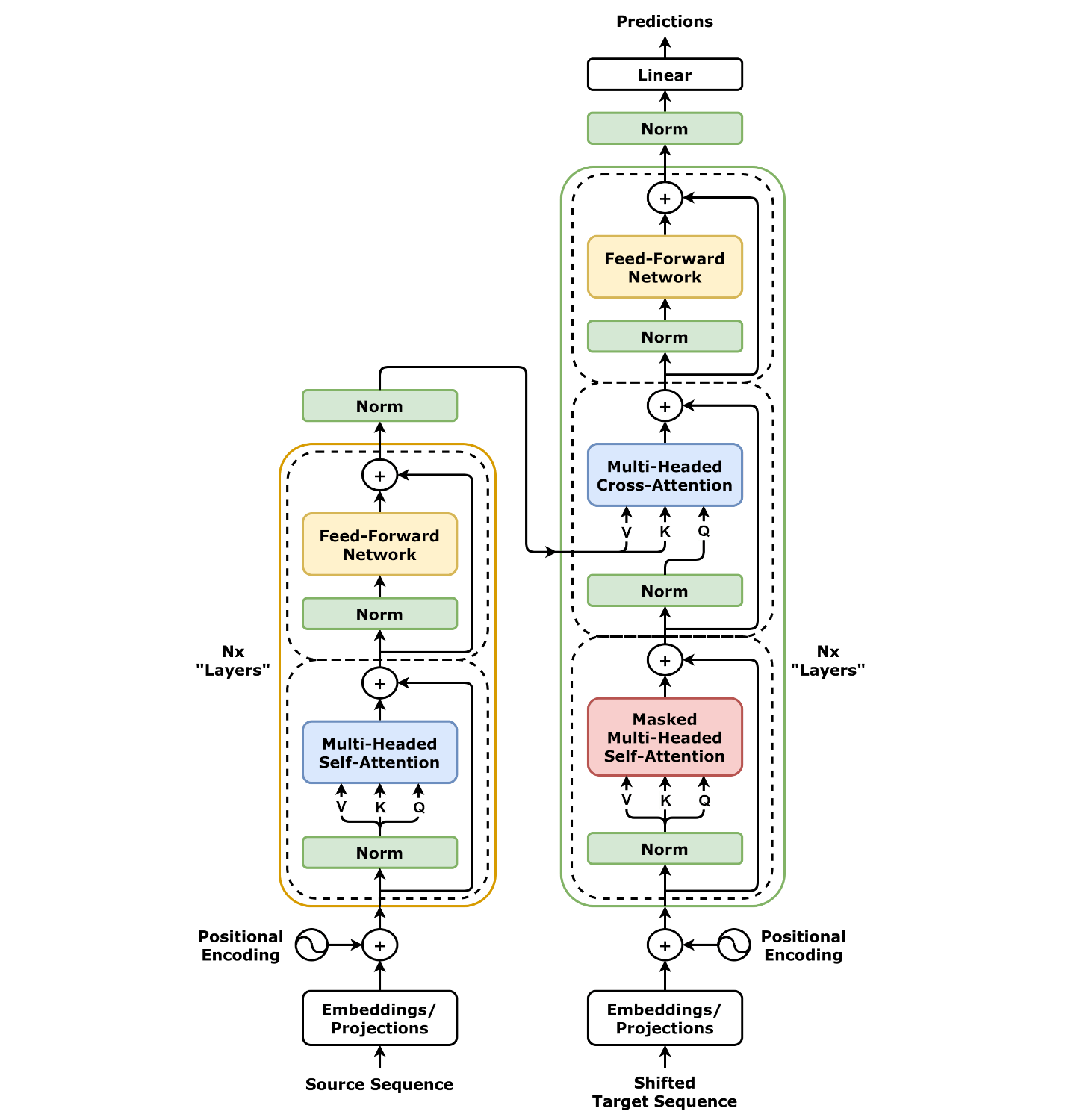
transformer左边是编码器,右边是解码器。编码器由NN个层组成,每层都包含了两个子层,分别是多头自注意力机制,计算输入序列中每个词与其他词的相关性,前馈神经网络,对每个词(token)进行非线性的变换。而在解码器中每层包含了三个子层。分别是掩码多头自注意力机制,计算输出序列中每个词与前面词的相关性。
pytorch的注意力机制实现和原理
在attention is all you need这篇论文中提出了多头注意力机制的概念,实现多头注意力机制是transformer模型的基础。多头注意力机制是将输入分为多个头,每个头去独立的计算,最终再合并。而缩放点积注意力是计算查询Q和键K的点积,缩放后使用 softmax 计算注意力权重,最后对值进行加权求和。掩码mask是用于屏蔽无效的位置。
在多头注意力初始化的时候有两个关键的参数,分别是模型的维度dimension意思就是输入的token的input id被embedding后对应的向量长度和注意力头数。这里应当注意的是,由于输入的维度要被分为多个头,故维度必须可以被注意力头数整除。随后建立了四个线性神经网络,q,v,k,o都是输入为模型维度,输出为模型维度。
python
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()#首先让其父类初始化
assert d_model % num_heads == 0, "d_model必须能被num_heads整除"
self.d_model = d_model # 模型维度(如512)
self.num_heads = num_heads # 注意力头数(如8)
self.d_k = d_model // num_heads # 每个头的维度(如64)
# 定义线性变换层(无需偏置)
self.W_q = nn.Linear(d_model, d_model) # 查询变换
self.W_k = nn.Linear(d_model, d_model) # 键变换
self.W_v = nn.Linear(d_model, d_model) # 值变换
self.W_o = nn.Linear(d_model, d_model) # 输出变换在设定了,q,k,v和维度,头数这些后。还需要写个缩放点积注意力的函数。
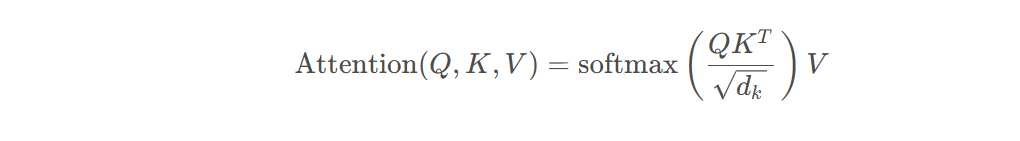
缩放点积注意力的关键公式如上,其中的QK(T)意味要求查询和键之间的点积,该矩阵表示了每个查询向量和键向量之间的相似度。正如AI所解释的:
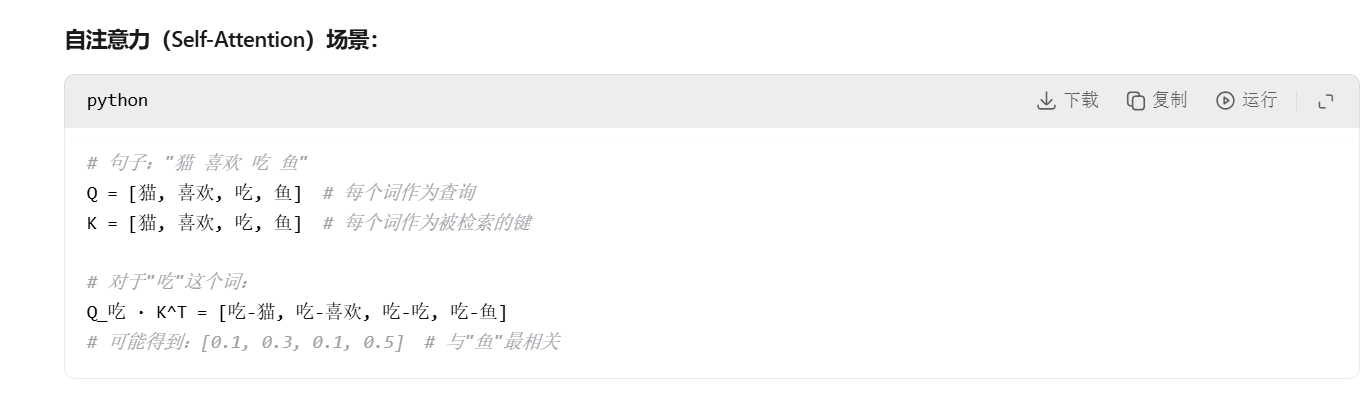
Q与K转置的点积表示了token之间的联系和相似,以此来学习语言中的词之间的关系。而缩放的目的是因为点积后的结果可能过大,为了防止梯度消失或者梯度爆炸,需要给除以一个常数sqrt(d_k)。随后再用个softmax函数来做归一化,通过 softmax 函数对每个查询的得分进行归一化,得到注意力权重矩阵。这些权重矩阵会表明每个查询向量对所有键向量的关注程度。softmax即通常的归一化标准化函数返回的是0-1内的值。
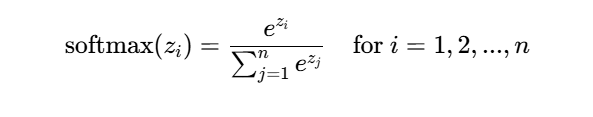
最后,将这些注意力权重与值矩阵 V 相乘,得到加权后的值,生成上下文向量。

AI给出了一个很有意思的范例,在这个范例中通过求解注意力机制可以对上下文的信息进行融合并建立联系。知道了原理之后再去看代码就会感觉很简单了。
python
def scaled_dot_product_attention(self, Q, K, V, mask=None):
"""
计算缩放点积注意力
输入形状:
Q: (batch_size, num_heads, seq_length, d_k)
K, V: 同Q
输出形状: (batch_size, num_heads, seq_length, d_k)
"""
# 计算注意力分数(Q和K的点积)
attn_scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
# 应用掩码(如填充掩码或未来信息掩码)
if mask is not None:
attn_scores = attn_scores.masked_fill(mask == 0, -1e9)
# 计算注意力权重(softmax归一化)
attn_probs = torch.softmax(attn_scores, dim=-1)
# 对值向量加权求和
output = torch.matmul(attn_probs, V)
return output后面还需要有分割为多头和整合多头的函数,其中的view函数用于重新塑造张量的维度为(batch_size,seq_length,self.num_heads,self.d_k)而transpose()函数用于交换维度。比如x = torch.randn(2, 3, 4, 5) ;y = x.transpose(1, 2) # 形状: (2, 4, 3, 5)
python
def split_heads(self, x):
"""
将输入张量分割为多个头
输入形状: (batch_size, seq_length, d_model)
输出形状: (batch_size, num_heads, seq_length, d_k)
"""
batch_size, seq_length, d_model = x.size()
return x.view(batch_size, seq_length, self.num_heads, self.d_k).transpose(1, 2)
def combine_heads(self, x):
"""
将多个头的输出合并回原始形状
输入形状: (batch_size, num_heads, seq_length, d_k)
输出形状: (batch_size, seq_length, d_model)
"""
batch_size, _, seq_length, d_k = x.size()
return x.transpose(1, 2).contiguous().view(batch_size, seq_length, self.d_model)之后还需要一个多头注意力机制的前向传播函数:
python
def forward(self, Q, K, V, mask=None):
"""
前向传播
输入形状: Q/K/V: (batch_size, seq_length, d_model)
输出形状: (batch_size, seq_length, d_model)
"""
# 线性变换并分割多头
Q = self.split_heads(self.W_q(Q)) # (batch, heads, seq_len, d_k)
K = self.split_heads(self.W_k(K))
V = self.split_heads(self.W_v(V))
# 计算注意力
attn_output = self.scaled_dot_product_attention(Q, K, V, mask)
# 合并多头并输出变换
output = self.W_o(self.combine_heads(attn_output))
return output思路就是首先求线性变换和注意力分头后的Q,K,V再求注意力,并且合并多头输出再变换。正如下图所示:
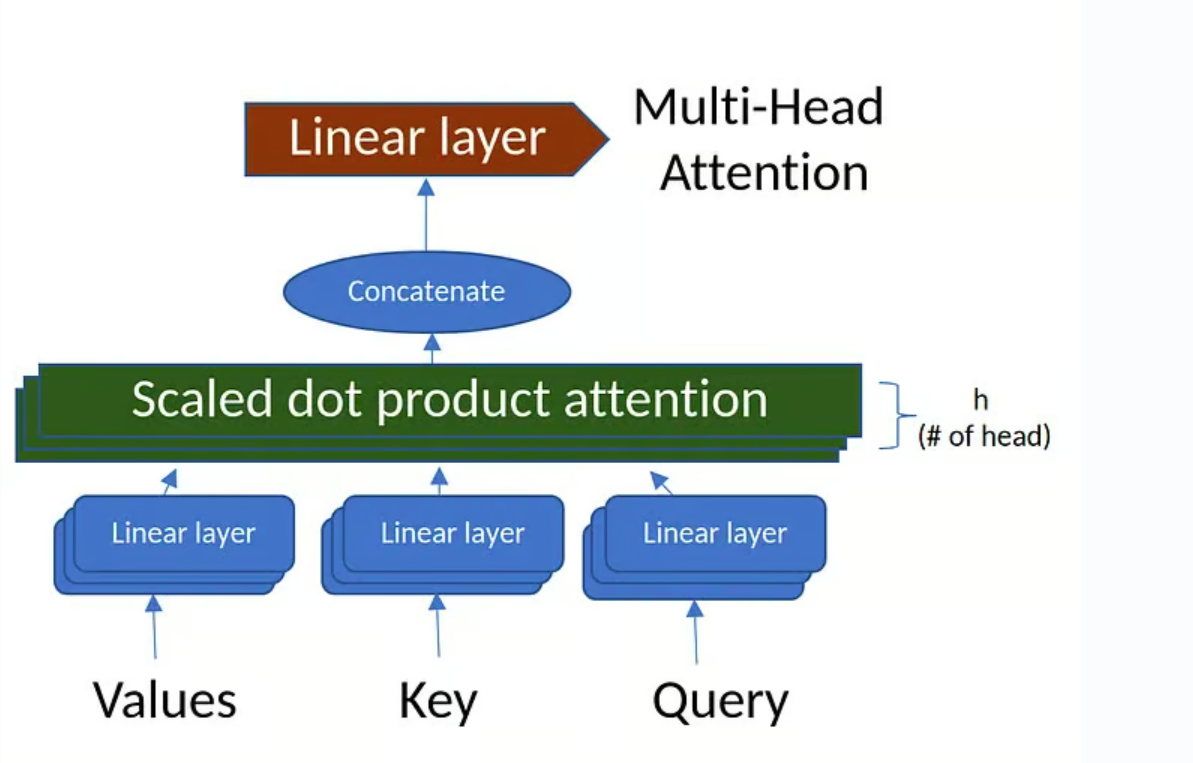
编码器,解码器
自注意力机制是通向编码器,解码器的基石,有了这两种就可以构建编码器解码器了。编码器模块的结构图示如下:
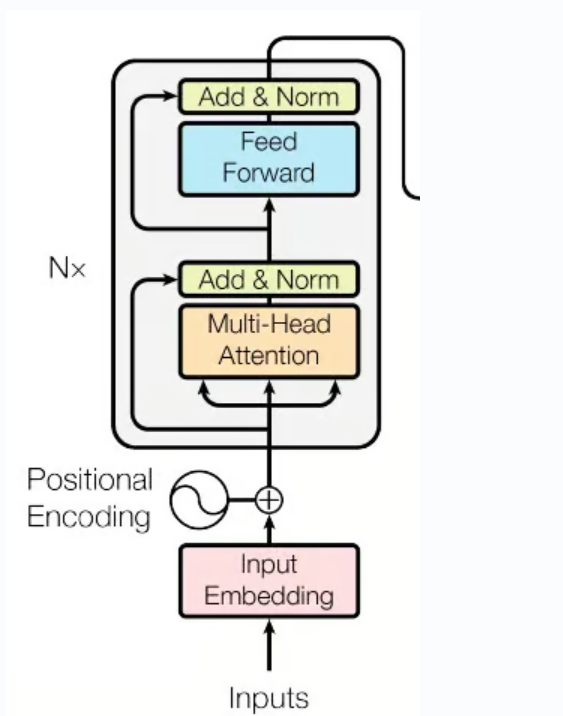
在编码器层包含一个多头自注意力机制和一个前馈网络(也就是Feed forward network,FFN位置前馈网络),每个子层后进行残差连接和归一化。FFN为多头注意力挖掘的上下文信息做非线性变换再次深度处理,下面是一个FFN的模块代码。
python
class positionWiseFeedForward(nn.Module):
def __init__(self,d_model,d_ff):#d_ff是feed_forward层的维数
super(poistionwiseFeedForward,self).__init__()#首先是父类的初始化
self.fc1=nn.Linear(d_model,d_ff)
self.fc2=nn.Linear(d_ff,d_model)
self.relu=nn.ReLU()
def forward(self,x):
return self.fc2(self.relu(self.fc1(x)))#实际上所谓feed_forward就是俩线性层加一个激活层的非线性变换在编码器模块中还有个位置编码模块,用于给序列中的每个token添加位置信息,因为Transformer本身没有递归结构,无法感知序列的顺序,感知到位置信息后,才能知晓这个Token在上下文中的位置。位置编码模块的代码如下所示,原理就是首先根据d_model也就是Token的编码向量长度,分奇数位和偶数位分别用sin和cos按照特定的频率来做位置编码。
python
class PositionalEncoding(nn.Module):#编码器用于注入输入序列中的每个token的位置信息,使用不同频率的正弦和余弦函数来生成位置编码
def __init__(self, d_model, max_seq_length):
super(PositionalEncoding, self).__init__()
pe = torch.zeros(max_seq_length, d_model) # 初始化位置编码矩阵,max_seq_length就是token的数目,d_model就是每个token的特征向量长度
position = torch.arange(0, max_seq_length, dtype=torch.float).unsqueeze(1)#展开poistion
div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(math.log(10000.0) / d_model))#此函数用于创建不同的频率,从0到d_model,每次渐进2
pe[:, 0::2] = torch.sin(position * div_term) # 偶数位置使用正弦函数,[0::2]是所有的偶数行
pe[:, 1::2] = torch.cos(position * div_term) # 奇数位置使用余弦函数,[1::2]是所有的奇数行
self.register_buffer('pe', pe.unsqueeze(0)) # 注册为缓冲区,上面根据奇数和偶数分别调用余弦频率编码和正弦频率编码
def forward(self, x):
# 将位置编码添加到输入中
return x + self.pe[:, :x.size(1)]#x+编码有了上述的这些模块就可以组合起来搭建编码器直接按照论文中的模块图进行搭建即可。代码如下:
python
class Encoderlayer(nn.Module):
def __init__(self,d_module,num_heads,d_ff,dropout):
super(Encoderlayer,self).__init__()
self.self_attn=MultiHeadAttention(d_module,num_heads)#自注意力
self.feed_forward=positionWiseFeedForward(d_module,d_ff)#位置前馈函数
self.norm1=nn.LayerNorm(d_module)
self.norm2=nn.LayerNorm(d_module)
self.dropout=nn.Dropout(dropout)#dropout防止拟合技术
def forward(self,x,mask):
attn_output=self.self_attn(x,x,x,mask)#直接调用自注意力
x=self.norm1(x+self.dropout(attn_output))
ff_output=self.feed_forward(x)#自注意力后再前馈
x=self.norm2(x+self.dropout(ff_output))#第二次add&norm
return x解码器比编码器要更加复杂一些,其包含一个自注意力层,一个交叉注意力层和一个前馈网络和若干个连接归一层。最后还用了softmax函数把结果输出为0-1之间的概率。编码器与解码器的区别还在于解码器实际上是一个循环推理的过程,正如循环神经网络一样。简单的理解来说,编码器仅仅做一个encoding,而解码器需要每次预测下一位的token。也就是为何解码器既有输入的output embedding而且还是右移一味的 ,还有一个输出output probabilities指向0-1概率。
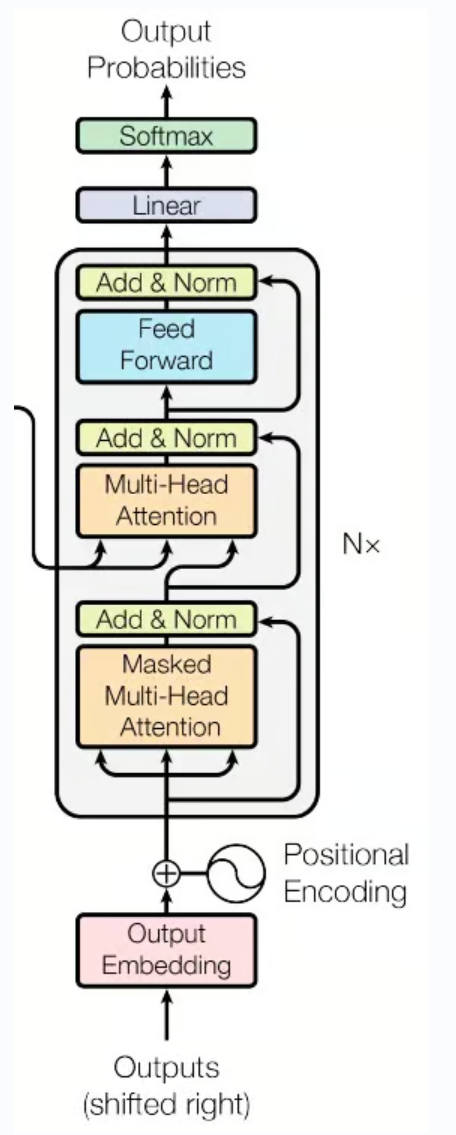
在transformer中,掩码主要的作用有两个,一个是屏蔽掉无效的padding区域,一个是屏蔽掉来自"未来"的信息。Encoder中的掩码主要是起到第一个作用,Decoder中的掩码则同时发挥着两种作用。
写好的transformer的解码器模块如下所示,值得主义的是,连接encoder和decoder模块的是交叉注意力,与自注意力机制的参数是不同的。
python
class Decoderlayer(nn.Module):
def __init__(self,d_module,num_heads,d_ff,dropout):
self.self_attn=MultiHeadAttention(d_module,num_heads)#自注意力机制
self.cross_attn=MultiHeadAttention(d_module,num_heads)#交叉注意力机制
self.feed_forward=positionWiseFeedForward(d_module,d_ff)#前馈网络
self.norm1=nn.LayerNorm(d_module)
self.norm2=nn.LayerNorm(d_module)
self.norm3=nn.LayerNorm(d_module)
self.dropout=nn.Dropout(dropout)
#交叉注意力相当于是对encoder的和decoder的算注意力,把编码和解码模块牵连起来
def forward(self,x,enc_output,src_mask,tgt_mask):
#先是自注意力机制
attn_output=self.self_attn(x,x,x,tgt_mask)#这里实际上默认调用的就是forward函数,这在基类中已经被写死了,所以传入的依次是Q,K,V和mask
x=self.norm1(x+self.dropout(attn_output))#第一次add&norm
attn_output=self.cross_attn(x,enc_output,enc_output,src_mask)#因为是交叉注意力,所以Q是x,K和V都是enc的输出,mask也是src_mask
x=self.norm2(x+self.dropout(attn_output))#第二次add&norm
ff_output=self.feed_forward(x)#再前馈函数一回
x=self.norm3(x+self.dropout(ff_output))#再add&norm
return xtransformer手撕与Pytorch实现
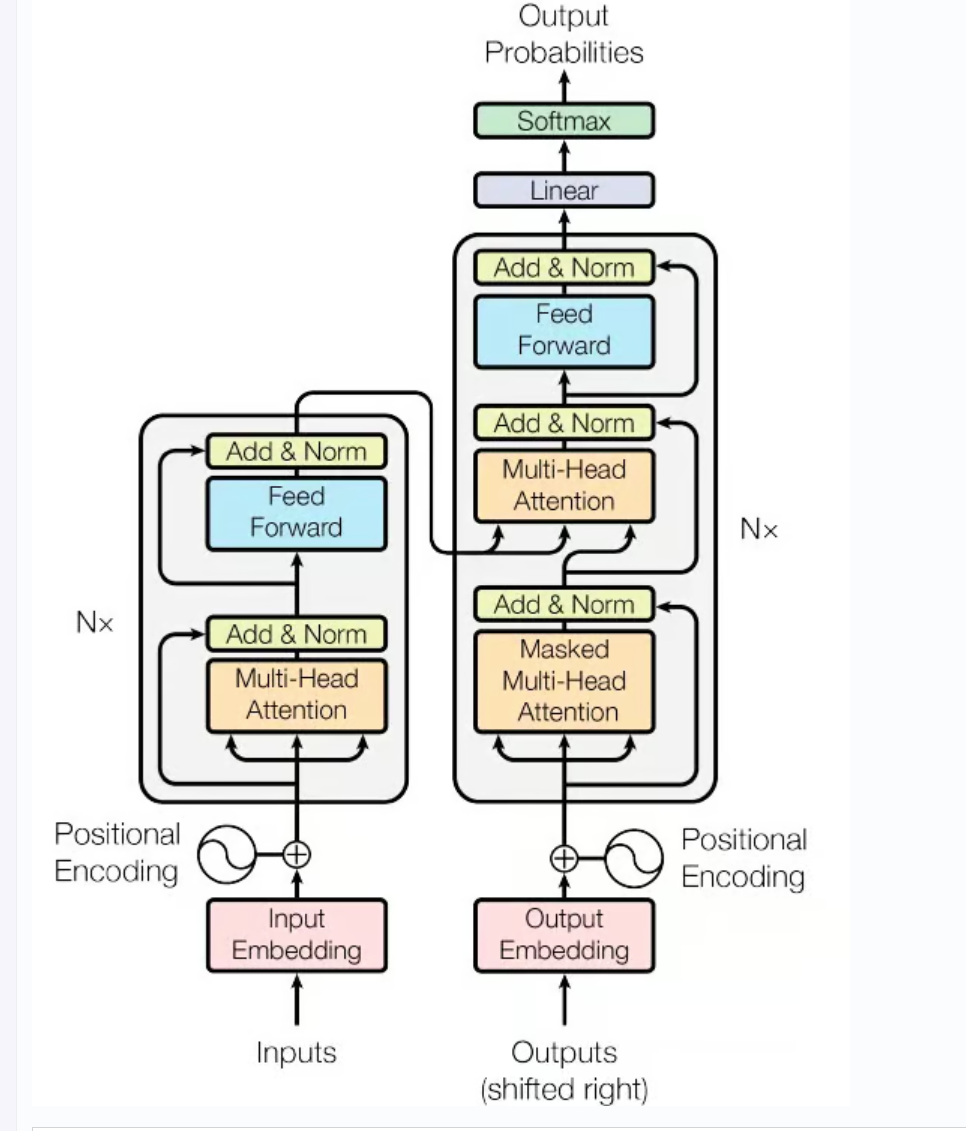
现在就明白了positional encoding这里为什么是个正弦函数,因为位置编码就是通过正弦函数和离散的频率来对token sequence进行编码。首先有个embedding,再有个positional encoding。
python
class Transformer(nn.Module):
def __init__(self, src_vocab_size, tgt_vocab_size, d_model, num_heads, num_layers, d_ff, max_seq_length, dropout):
super(Transformer, self).__init__()
self.encoder_embedding = nn.Embedding(src_vocab_size, d_model) # 编码器词嵌入
self.decoder_embedding = nn.Embedding(tgt_vocab_size, d_model) # 解码器词嵌入
self.positional_encoding = PositionalEncoding(d_model, max_seq_length) # 位置编码
# 编码器和解码器层
self.encoder_layers = nn.ModuleList([EncoderLayer(d_model, num_heads, d_ff, dropout) for _ in range(num_layers)])
self.decoder_layers = nn.ModuleList([DecoderLayer(d_model, num_heads, d_ff, dropout) for _ in range(num_layers)])
self.fc = nn.Linear(d_model, tgt_vocab_size) # 最终的全连接层
self.dropout = nn.Dropout(dropout) # Dropout
def generate_mask(self, src, tgt):
# 源掩码:屏蔽填充符(假设填充符索引为0)
# 形状:(batch_size, 1, 1, seq_length)
src_mask = (src != 0).unsqueeze(1).unsqueeze(2)
# 目标掩码:屏蔽填充符和未来信息
# 形状:(batch_size, 1, seq_length, 1)
tgt_mask = (tgt != 0).unsqueeze(1).unsqueeze(3)
seq_length = tgt.size(1)
# 生成上三角矩阵掩码,防止解码时看到未来信息
nopeak_mask = (1 - torch.triu(torch.ones(1, seq_length, seq_length), diagonal=1)).bool()
tgt_mask = tgt_mask & nopeak_mask # 合并填充掩码和未来信息掩码
return src_mask, tgt_mask
def forward(self, src, tgt):#src是source源序列的掩码,tgt是target,目标序列的掩码
# 生成掩码
src_mask, tgt_mask = self.generate_mask(src, tgt)#为编码器和解码器生成src_mask和tgt_mask
# 编码器部分
src_embedded = self.dropout(self.positional_encoding(self.encoder_embedding(src)))
#上面的代码按照流程图就是输入的embed_ed是先encoder_embedding求嵌入编码,再做位置编码
enc_output = src_embedded#初始化enc_output,实际上enc_output不是src_embedded
for enc_layer in self.encoder_layers:#循环遍历
enc_output = enc_layer(enc_output, src_mask)#每次循环后,都把上一轮的enc_output和src_mask输入
# 解码器部分
tgt_embedded = self.dropout(self.positional_encoding(self.decoder_embedding(tgt)))#要先预计有个tgt作为输入,也是先给embedding获得编码再位置编码
dec_output = tgt_embedded#先初始化dec_output
for dec_layer in self.decoder_layers:
dec_output = dec_layer(dec_output, enc_output, src_mask, tgt_mask)#每次循环过程中,由于decoder要和encoder发生联系,所以把上一轮的dec_output和下一轮的enc_output和两个mask都输入
# 最终输出
output = self.fc(dec_output)#按照图中所示,output还需要过一个全连接层,fc即full connection
return output