数据结构_深入理解堆（大根堆 小根堆）与优先队列：从理论到手撕实现

目录

• [一、大根堆和小根堆的概念（Max_Heap AND Min_Heap）](#一、大根堆和小根堆的概念（Max_Heap AND Min_Heap）)
• • 大根堆（Max_Heap）
  • 小根堆（Min_Heap）
• [二、 优先队列（Priority_Queue）](#二、 优先队列（Priority_Queue）)
• • 优先队列的要求
• 三、手撕优先队列
• • Priority_Queue数据结构定义
  • 优先队列的结构操作
  • • 访问队首元素
    • 弹出队首元素
    • 判定是否为空
    • 向下调整
    • 插入元素
    • 判满
    • 向上调整
    • 获取节点(左、右、父)
    • 交换
    • 输出队列
    • 释放内存
    • 堆排序

一、大根堆和小根堆的概念（Max_Heap AND Min_Heap）

大根堆（Max_Heap）

通俗点来说：根节点值最大，且每个父节点值 ≥ 子节点值的完全二叉树。

最大堆（又称大根堆）是二叉堆的两种形式之一，其根结点的关键字为堆内所有结点的最大值，且任一子树同样满足该性质。作为完全二叉树，最大堆的结构特性要求每个父节点的值不小于其子节点，采用数组存储以实现高效的元素访问与操作。

最大堆源于二叉堆的理论体系，早期基于完全二叉树实现父子节点有序性维护。后续发展为k叉堆等变体以提高特定场景的操作效率。其核心操作包含插入元素时的上浮调整与删除堆顶时的下沉调整。该数据结构被广泛应用于优先队列实现，支撑堆排序算法实现，并通过堆化过程生成满足完全二叉树性质的最大堆结构。

小根堆（Min_Heap）

通俗点来说：根节点值最小，且每个父节点值 ≤ 子节点值的完全二叉树

最小堆（又称小根堆）是一种基于完全二叉树结构的数据类型，其核心特性为任意非叶节点的值不大于左右子节点，根节点始终为堆内最小元素。数据通常以数组形式存储，通过父子节点下标公式（如父节点i的子节点为2i+1和2i+2）实现逻辑映射。堆支持插入元素时的上浮调整和删除最小值时的下沉调整操作，时间复杂度均为O(log n)。

该结构自概念提出后，逐步形成系统化实现方法：早期通过自底向上筛选算法构建堆，时间复杂度优化至O(n)；插入操作采用末尾添加后上浮比较的策略，删除操作则通过替换根节点后递归下沉维持有序性。随着应用场景扩展，最小堆被应用于优先级队列、海量数据极值筛选及定时器管理等工程领域，并与堆排序算法结合，实现时间复杂度为O(n log n)的高效排序。

二、 优先队列（Priority_Queue）

优先级队列是一种元素按优先权排序的数据结构，优先权最高（数值最小或最大）的元素可被优先访问和删除。基本操作包括查找、插入和删除，对于优先权相同的元素，可按先进先出次序处理或按任意优先权进行。其实现方式包含二叉堆（父节点优先级高于子节点）和无序数组（删除需遍历查找）。典型应用涵盖堆排序、哈夫曼编码构造。

通俗点来说，就是在一个特殊的队列中，这个队列并不是按照先进先出的顺序来的，每个人都有一个属于自己的权值，先后的顺序完全取决于自身的权值，按照重要程度来进行排队。例如：在公路上发生堵车时，等着通车，这时在车流的最后来了一辆拉着警笛的消防车，那么这时，公路上的车就要让出位置，让消防车率先通行，到达车流的最前端。这就是优先队列的基本概念。它也是一种数据结构，按照自身的优先级进行排序，优先级高的始终位于队伍的最前端。

优先队列的要求

• 队首是当前最高优先级元素

• 删除队首后，新的队首是剩余元素中最高优先级的

• 插入新元素时，它会被放到正确的位置

• 整个结构维护着完整的优先级关系

三、手撕优先队列

Priority_Queue数据结构定义

根据之前的经验，在书写数据结构之前要先有一个明确的数据定义,优先队列，需要一个数组来存储数据，需要一个整形变量来记录当前数组有多少个元素，还需要一个整形变量来记录当前数组总共可以存储多少个元素。

根据用户传入的 n 来当作大小，数组也按照这个 n 来开辟

typedef struct{
	int *data;//数组来存储数据
	int n,size;//n代表当前有多少个元素，size代表当前优先队列总共可以存储多少个元素
}Priority_Queue; 

优先队列的结构操作

对于优先队列这个数据结构的操作一般有

访问队首元素，弹出队首元素，插入元素，判空和判满

默认大根堆，我们宏定义#define cmp <

一般来说我们的数组从 1 开始存储数据，这样更方便得到当前节点的左孩子和右孩子（后面会说到具体的作用）

访问队首元素

我们可以宏定义 ROOT 这个堆的根为1

于是我们每次只需要返回根元素

//获取堆顶元素
int top(Priority_Queue * p){
	return p->data[ROOT]; 
} 

传入一个优先队列，直接返回这个队列的队首元素

弹出队首元素

在弹出队首元素时，相当于直接覆盖掉了，删除一个元素的位置，所以我们可以直接让数据的最后一个元素直接覆盖掉队首元素，进行重新调整。

话不多说上图：

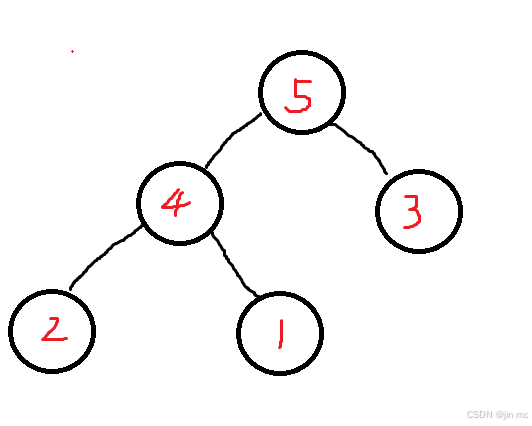
例如：这个堆的堆顶元素为 5 ，现在我们要删除它

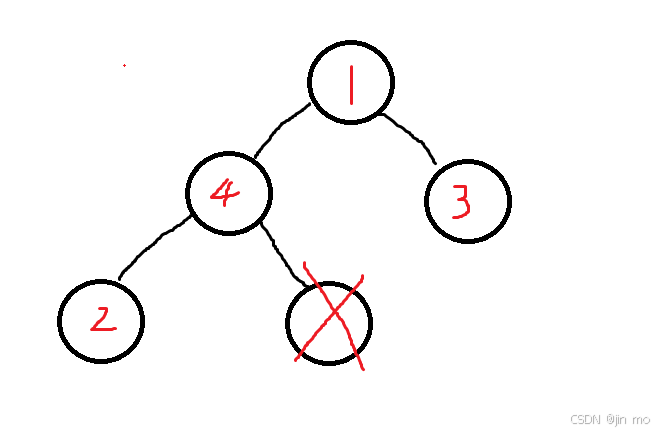
我们直接用数组最后一个元素将堆顶元素覆盖，将数组中个数减一，接着向下不断调整

经过一次调整：

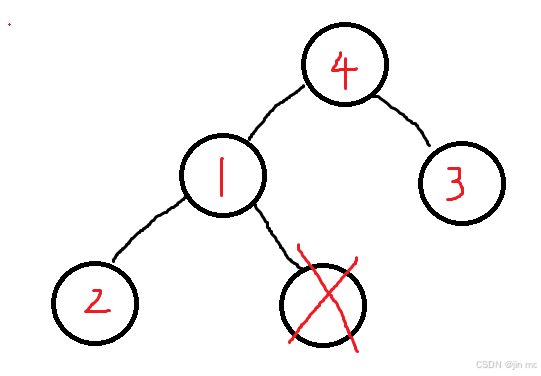
经过两次调整：

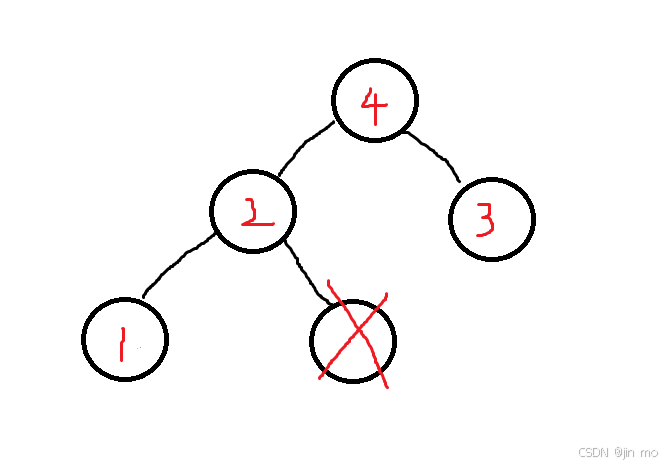
可见，通过不断地调整吧，我们成功的将堆顶元素删除了，然后将下一个最大的元素调整到了堆顶。

//删除
int pop(Priority_Queue * p){
	if(empty(p)){
		printf("优先队列为空，无法删除\n");
		return 0;
	}
	//使用最后一个元素直接覆盖掉根元素，重新排列
	p->data[ROOT] = p->data[(p->n)--];
	//向下更新
	down_update(p,ROOT); 
	return 1;
} 

判定是否为空

没什么说的直接返回，n是否等于0

bool empty(Priority_Queue * p){
	return p->n==0; 
}

向下调整

这段代码是重重之重

根据二叉树的概念，左孩子为当前节点的索引 * 2，右孩子为（当前节点 *2+1），调整的时候，看的是当前节点的左右孩子，分别对比，才可以确认最后需要调整到左边还是右边

//向下更新
void down_update(Priority_Queue * p, int i){
	//分别表示左右孩子和当前三个元素的最大值的索引 
	int left,right,ind=i;
	while(getLeft(i) <= p->n){
		left=getLeft(i);
		right=getRight(i);
		ind = i ;
		if(p->data[ind] cmp p->data[left]){
			ind=left;
		}
		//由于循环逻辑中只判断了是否有左孩子，没有判断右孩子，所以这里需要做一个边界检查 
		if(right <= p->n && p->data[ind] cmp p->data[right]){
			ind=right;
		}
		if(ind==i) break;
		swap(p->data[ind],p->data[i]);
		i=ind;
	}
	return;
} 

循环的条件为：当前的节点至少需要存在一个左节点，才有可能调整。

之后获取当前节点的左孩子和右孩子，记录三个节点中最大的节点为 ind 也就是看需要向哪边调整，最初记录为当前传入的节点 i

先跟左孩子比较，如果小于左孩子，那么将左孩子提上来，更改最大的节点 ind 为 left ,按照同样的方法检查右孩子。如果最终判断完，最大的节点还是我们传入的节点，那么就证明不需要调整，当前的 i 节点已经是最大的了

插入元素

直接插入到最后一个位置，进行向上更新

//插入 
int push(Priority_Queue *p,int val){
	if(full(p)){
		printf("优先队列已满\n");
		return 0;
	}
	//插入到队列的最后一个元素的位置，进行n++
	//赋值
	p->data[++(p->n)]=val;
	//向上更新
	up_update(p->data,p->n);
	return 1; 
}

判满

只需要判断数组中元素的个数是否等于最大可容纳元素数量

//判满 
bool full(Priority_Queue * p){
	return p->n==p->size;
}

向上调整

相较于向下调整，向上调整稍微简单一点点

一直从数组的最后一个元素，向其父节点比较，只要大于其父节点就交换

//向上更新
void up_update(int * data,int i){
	if(i==ROOT) return;
	//获取当前节点的父节点 
	int father=getFather(i);
	if(data[father] cmp data[i]){
		swap(data[father],data[i]);
		up_update(data,father);
	}
	return;
} 

直接使用递归解决，只要当前节点为根节点，那么就停止，直接返回，要不就一直交换

获取节点(左、右、父)

//获取左节点 
int getLeft(int i){
	return i*2;
}
//获取右节点 
int getRight(int i){
	return i*2+1;
}
//获取父节点 
int getFather(int i){
	return i/2;
}

交换

使用了c++的特性，引用

//交换
void swap(int &a,int &b){
	int t=a;
	a=b;
	b=t;
	return;	
}

这下主要的函数都写完了，下来写点工具，更方便我们直观的观察

输出队列

void output(Priority_Queue *p){
	printf("Priority_Queue : ");
	for(int i=1;i<=p->n;i++){
		printf("%d ",p->data[i]);
	}
	printf("\n");
	return;
}

释放内存

//释放内存 
void clear(Priority_Queue *q){
	free(q->data);
	free(q);
	return;
}

利用好优先队列，我们还可以进行排序，由于大根堆，队首元素永远是最大的，利用这个特性，我们可以创建一个当前队列的副本，记录副本队列的队首元素，然后将其队首弹出，直到队列为空

堆排序

void getSort(Priority_Queue * original){
	int index=0; 
	int sort[MAX_NUM]; 
	// 创建副本
    Priority_Queue * p = init_Priority_Queue(original->size);
    if(p == NULL) return;  // 添加检查
    p->n = original->n;
    //数据复制 
    for(int i = 1; i <= original->n; i++){
        p->data[i] = original->data[i];
    }
	while(!empty(p)){
		sort[index++]= top(p);
		pop(p);
	}
	printf("堆排序 : ");
	for(int i=0;i<index;i++){
		printf("%d ",sort[i]);
	}
	printf("\n");
	clear(p); 
	return;  
} 

详细代码如下，可以更加深刻的理解：

//大根堆 优先队列 
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#define ROOT 1
#define cmp <
#define MAX_NUM 10

typedef struct{
	int *data;
	int n,size;
}Priority_Queue; 
//初始化 
Priority_Queue *init_Priority_Queue(int n){
	Priority_Queue * p=(Priority_Queue*)malloc(sizeof(Priority_Queue));
	if(p==NULL){
		printf("Error\n");
		exit(-1);
	}
	p->data = (int*)malloc(sizeof(int)*(n+1));
	p->n=0;
	p->size=n;
	return p;
}
//获取左节点 
int getLeft(int i){
	return i*2;
}
//获取右节点 
int getRight(int i){
	return i*2+1;
}
//获取父节点 
int getFather(int i){
	return i/2;
}
//判空
bool empty(Priority_Queue * p){
	return p->n==0; 
}
//判满 
bool full(Priority_Queue * p){
	return p->n==p->size;
}
void swap(int &a,int &b){
	int t=a;
	a=b;
	b=t;
	return;	
}
//向上更新
void up_update(int * data,int i){
	if(i==ROOT) return;
	//获取当前节点的父节点 
	int father=getFather(i);
	if(data[father] cmp data[i]){
		swap(data[father],data[i]);
		up_update(data,father);
	}
	return;
} 
//插入 
int push(Priority_Queue *p,int val){
	if(full(p)){
		printf("优先队列已满\n");
		return 0;
	}
	//插入到队列的最后一个元素的位置，进行n++
	//赋值
	p->data[++(p->n)]=val;
	//向上更新
	up_update(p->data,p->n);
	return 1; 
}
//获取堆顶元素
int top(Priority_Queue * p){
	return p->data[ROOT]; 
} 
//向下更新
void down_update(Priority_Queue * p, int i){
	//分别表示左右孩子和当前三个元素的最大值的索引 
	int left,right,ind=i;
	while(getLeft(i) <= p->n){
		left=getLeft(i);
		right=getRight(i);
		ind = i ;
		if(p->data[ind] cmp p->data[left]){
			ind=left;
		}
		//由于循环逻辑中只判断了是否有左孩子，没有判断右孩子，所以这里需要做一个边界检查 
		if(right <= p->n && p->data[ind] cmp p->data[right]){
			ind=right;
		}
		if(ind==i) break;
		swap(p->data[ind],p->data[i]);
		i=ind;
	}
	return;
} 
//删除
int pop(Priority_Queue * p){
	if(empty(p)){
		printf("优先队列为空，无法删除\n");
		return 0;
	}
	//使用最后一个元素直接覆盖掉根元素，重新排列
	p->data[ROOT] = p->data[(p->n)--];
	//向下更新
	down_update(p,ROOT); 
	return 1;
	 
} 
//释放内存 
void clear(Priority_Queue *q){
	free(q->data);
	free(q);
	return;
}
void output(Priority_Queue *p){
	printf("Priority_Queue : ");
	for(int i=1;i<=p->n;i++){
		printf("%d ",p->data[i]);
	}
	printf("\n");
	return;
}
void getSort(Priority_Queue * original){
	int index=0; 
	int sort[MAX_NUM]; 
	// 创建副本
    Priority_Queue * p = init_Priority_Queue(original->size);
    if(p == NULL) return;  // 添加检查
    p->n = original->n;
    //数据复制 
    for(int i = 1; i <= original->n; i++){
        p->data[i] = original->data[i];
    }
	while(!empty(p)){
		sort[index++]= top(p);
		pop(p);
	}
	printf("堆排序 : ");
	for(int i=0;i<index;i++){
		printf("%d ",sort[i]);
	}
	printf("\n");
	clear(p); 
	return;  
} 
#define MAX_OP 10

int main()
{
	Priority_Queue *p=init_Priority_Queue(MAX_NUM);
	for(int i=0;i<MAX_OP;i++){
		int op;scanf("%d",&op);
		if(op==1){
			int val;scanf("%d",&val);
			push(p,val);
		}else{
			
			pop(p);
		}
		output(p);
	} 
	getSort(p);
	return 0;
}