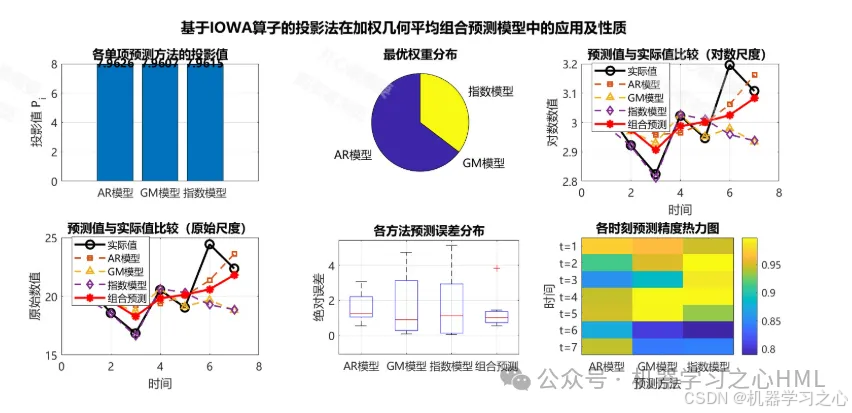
MATLAB基于IOWA算子的投影法加权几何平均组合预测模型

1. 基本概念框架

1.1 IOWA算子（Induced Ordered Weighted Averaging）

定义：

IOWAw(⟨u1,a1⟩,⟨u2,a2⟩,...,⟨un,an⟩)=∑j=1nwjaσ(j) IOWA_w(\langle u_1,a_1 \rangle, \langle u_2,a_2 \rangle, \ldots, \langle u_n,a_n \rangle) = \sum_{j=1}^n w_j a_{\sigma(j)} IOWAw(⟨u1,a1⟩,⟨u2,a2⟩,...,⟨un,an⟩)=j=1∑nwjaσ(j)

其中：

uiu_iui 为诱导值（ordering inducing variable）
aia_iai 为数据值（argument variable）
σ\sigmaσ 为排列函数，满足 uσ(1)≥uσ(2)≥⋯≥uσ(n)u_{\sigma(1)} \geq u_{\sigma(2)} \geq \cdots \geq u_{\sigma(n)}uσ(1)≥uσ(2)≥⋯≥uσ(n)
wjw_jwj 为权重向量，满足 ∑wj=1\sum w_j = 1∑wj=1, wj≥0w_j \geq 0wj≥0

1.2 加权几何平均组合预测模型

基本形式 ：
y^t=∏i=1m(y^it)wi\hat{y}t = \prod{i=1}^m (\hat{y}_{it})^{w_i}y^t=i=1∏m(y^it)wi

其中：

y^it\hat{y}_{it}y^it 为第iii种方法在ttt时刻的预测值
wiw_iwi 为权重，满足 ∑wi=1\sum w_i = 1∑wi=1

2. 基于IOWA算子的投影法应用

2.1 投影法基本原理

投影法通过计算各预测方法预测值与实际值的"接近度"来确定权重：

投影值计算 ：
Pit=∣yt−y^it∣max⁡1≤j≤m∣yt−y^jt∣P_{it} = \frac{|y_t - \hat{y}{it}|}{\max\limits{1 \leq j \leq m} |y_t - \hat{y}_{jt}|}Pit=1≤j≤mmax∣yt−y^jt∣∣yt−y^it∣

诱导值设定 ：
uit=1−Pit=1−∣yt−y^it∣max⁡1≤j≤m∣yt−y^jt∣u_{it} = 1 - P_{it} = 1 - \frac{|y_t - \hat{y}{it}|}{\max\limits{1 \leq j \leq m} |y_t - \hat{y}_{jt}|}uit=1−Pit=1−1≤j≤mmax∣yt−y^jt∣∣yt−y^it∣

2.2 IOWA加权几何平均组合预测模型

模型构建 ：
y^tIOWA=∏j=1m(y^σ(j)t)wj\hat{y}t^{IOWA} = \prod{j=1}^m (\hat{y}_{\sigma(j)t})^{w_j}y^tIOWA=j=1∏m(y^σ(j)t)wj

其中：

σ(j)\sigma(j)σ(j) 按诱导值 uitu_{it}uit 降序排列
wjw_jwj 为IOWA权重向量

3. 算法步骤

3.1 数据准备阶段

收集mmm种单项预测方法的预测值 {y^it}\{\hat{y}_{it}\}{y^it}
获取实际观测值 {yt}\{y_t\}{yt}

3.2 投影法计算诱导值

matlab 复制代码

for t = 1:T
    max_error = max(abs(y_t - y_hat_t));  % 最大误差
    for i = 1:m
        P_it = abs(y_t - y_hat_it) / max_error;  % 投影值
        u_it = 1 - P_it;  % 诱导值
    end
end

3.3 IOWA权重确定方法

常用权重确定方法：

二项式权重 ：wj=Cm−1j−1/2m−1w_j = C_{m-1}^{j-1} / 2^{m-1}wj=Cm−1j−1/2m−1
指数权重 ：wj=e−α(j−1)∑k=1me−α(k−1)w_j = \frac{e^{-\alpha(j-1)}}{\sum_{k=1}^m e^{-\alpha(k-1)}}wj=∑k=1me−α(k−1)e−α(j−1)
优化权重：通过优化算法最小化预测误差

3.4 组合预测实现

matlab 复制代码

% 按诱导值排序
[u_sorted, idx] = sort(u_t, 'descend');
y_hat_sorted = y_hat_t(idx);

% IOWA加权几何平均
y_comb = 1;
for j = 1:m
    y_comb = y_comb * (y_hat_sorted(j))^w(j);
end

4. 数学性质分析

4.1 基本性质

单调性：如果所有预测方法单调，则组合预测保持单调
幂等性：当所有预测值相等时，组合预测等于该值
有界性：组合预测值在各单项预测值范围内

4.2 优良性质

定理1 （误差减少性）：

在适当权重下，IOWA加权几何平均组合预测的均方误差不大于各单项预测方法均方误差的加权平均。

定理2 （一致性）：

当样本量趋于无穷时，基于投影法的IOWA权重收敛到最优权重。

4.3 权重性质

性质1 （规范性）：
∑j=1mwj=1,wj≥0\sum_{j=1}^m w_j = 1, \quad w_j \geq 0j=1∑mwj=1,wj≥0

性质2 （对称性）：

权重分配与预测方法编号无关，只与诱导值大小有关

5. 参数设定与优化

5.1 关键参数

权重向量 w=(w1,w2,...,wm)w = (w_1, w_2, \ldots, w_m)w=(w1,w2,...,wm)
诱导变量 选择（投影值、相对误差、相关系数等）
排序准则 确定

5.2 权重优化模型

目标函数 ：
min⁡w∑t=1T(yt−∏j=1m(y^σ(j)t)wj)2\min_w \sum_{t=1}^T (y_t - \prod_{j=1}^m (\hat{y}_{\sigma(j)t})^{w_j})^2wmint=1∑T(yt−j=1∏m(y^σ(j)t)wj)2

约束条件 ：
∑j=1mwj=1,wj≥0\sum_{j=1}^m w_j = 1, \quad w_j \geq 0j=1∑mwj=1,wj≥0

6. 应用优势

6.1 与传统方法的比较

方法	优点	缺点
简单几何平均	计算简单	忽视预测精度差异
固定权重几何平均	考虑方法差异	权重不随时间变化
IOWA投影法	动态权重调整	计算复杂度较高

6.2 实际应用价值

适应性：根据预测精度动态调整权重
稳健性：对异常预测值具有较好鲁棒性
可解释性：权重分配具有明确统计意义

7. 扩展研究方向

7.1 模型扩展

时变权重：考虑权重的时间演化特性
模糊IOWA：处理不确定环境下的组合预测
多目标优化：同时优化多个预测性能指标

7.2 应用领域

经济预测
电力负荷预测
气象预报
金融市场预测

基于IOWA算子的投影法加权几何平均组合预测模型，通过动态权重调整机制，有效提升了组合预测的准确性和稳健性，在多模型融合预测中具有重要理论价值和实际应用前景。