南京大学LLM开发基础（四）MoE, LoRA, 数的精度 + MLP层实验

https://njudeepengine.github.io/llm-course-lecture/2025/lecture8.html#1

目录

[1. Mixture-of-experts (MoE)](#1. Mixture-of-experts (MoE))

[1.1 优势](#1.1 优势)

[1.2 结构](#1.2 结构)

[1.3 训练](#1.3 训练)

[2. Low-rank adaptation (LoRA)](#2. Low-rank adaptation (LoRA))

[3. 数的精度 -- 混合精度 + 量化操作](#3. 数的精度 -- 混合精度 + 量化操作)

Task1：DenseMLPWithLoRA

一、任务背景

二、任务要求

[Task2：Sparse MLP](#Task2：Sparse MLP)

---

1. Mixture-of-experts (MoE)

通过gating model/network 选择最适合的专家。

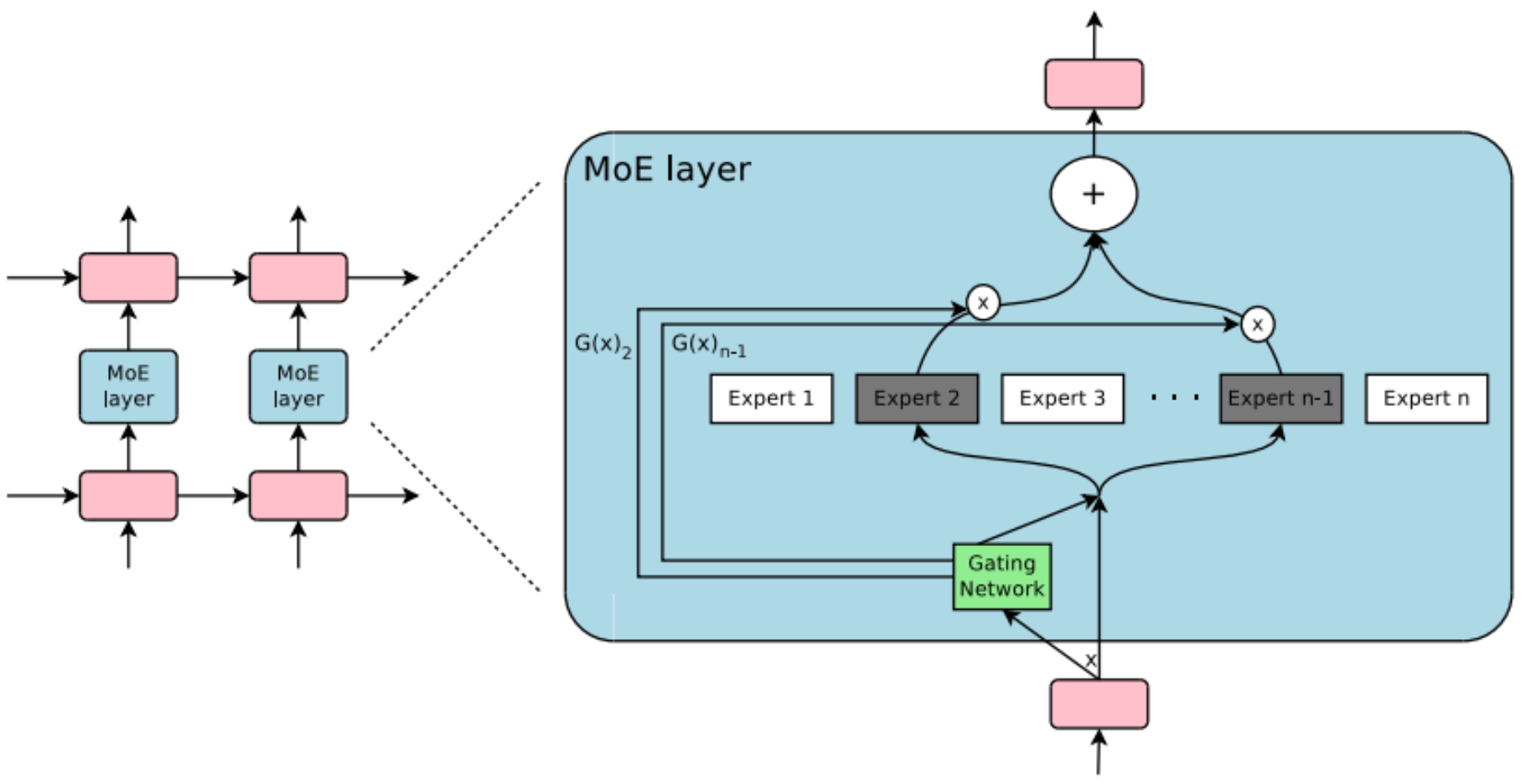
Switch Transformers 将Transformers中的 FFN替换为MoE 结构。

1.1 优势

1. 推理阶段的效率提升：

每次只用一部分 专家的参数；条件计算 与动态资源分配

门控网络会根据输入样本的难度和类型 ，动态地选择最合适的专家。

处理简单任务时： 模型可能会路由到一些相对"简单"或计算量较小的专家，从而更快地给出响应。

处理复杂任务时： 模型会调用**更"专业"**的专家，虽然计算量稍大，但能保证输出质量。

2. 以恒定计算成本 ，实现模型参数规模的巨量提升。

• 传统模型（稠密模型）： 增加参数意味着每一层、每一个输入都要经过所有这些参数的计算。模型变大，计算成本（FLOPS）和时间几乎线性增长。

• MoE 模型（稀疏模型）： 模型总参数量可以变得极其巨大（例如万亿参数），但对于每个具体的输入，只有一小部分"专家"（通常是1个或2个）被激活并参与计算。这意味着：

  • 总参数量巨大：模型拥有海量的知识和能力储备。

  • 激活参数量固定：无论总参数是千亿还是万亿，处理一个 token 实际使用的参数数量是基本不变的，因此计算成本得以保持在一个可接受的水平。

3. 预训练速度显著加快：

在相同的计算资源 （如相同的GPU数量和训练时间）下，MoE 模型能获得比稠密模型更好的性能

1.2 结构

topk 得到前 k 名，对分数 softmax 得到每个export权重。

class TopKGating(nn.Module):
    def __init__(self, hidden_dim, num_experts, k=2):
        super().__init__()
        self.router = nn.Linear(hidden_dim, num_experts, bias=False)  # 路由网络
        self.k = k  # 选择专家数量
    def forward(self, x):
        # 1. 计算专家得分
        scores = self.router(x)  # [batch, experts]
        # 输入x: [batch_size, hidden_dim]
        # 输出scores: [batch_size, num_experts]
        # 每个样本对每个专家得到一个得分
        
        # 2. 选择Top-K专家
        topk_scores, topk_idx = torch.topk(scores, self.k, dim=-1)
        # topk_scores: [batch_size, k] - 前k个最高得分
        # topk_idx: [batch_size, k] - 对应的专家索引
        
        # 3. 计算选择概率
        probs = torch.softmax(topk_scores, dim=-1)
        # 对选中的k个专家得分做softmax，得到归一化的权重
        
        # 4. 构建门控矩阵
        gate = torch.zeros_like(scores)  # 创建全零矩阵 [batch_size, num_experts]
        gate.scatter_(-1, topk_idx, probs)  # 将概率值填充到对应位置
        # 结果gate: [batch_size, num_experts]，每行只有k个非零值

1.3 训练

训练不稳定性问题：

• 强者恒强：某些专家训练得快，获得更高权重，被选择更多

• 弱者淘汰：其他专家得不到充分训练，逐渐被边缘化

• 模式坍塌 ：最终只有少数专家被使用

下面三个解决方案：

1. Auxiliary Loss 辅助损失：均衡各个专家的选择概率。

• 计算每个专家被选择的概率分布

• 计算批次中实际选择每个专家的频率分布

• 惩罚这两个分布之间的差异，鼓励均匀分布

2. Capacity Factor 容量因子

预先计算每个专家的"容量" 处理token数量上限。多余的强制给别的expert。

3. Shared Experts 共享专家机制

设计专家架构时（不同损失函数）就将专家分为"通用型"和"专用型"。

• 共享专家 ：处理通用模式和基础特征，保证基本利用率

• 专用专家 ：学习特定领域或复杂模式，允许一定程度的专业化

2. Low-rank adaptation (LoRA)

https://arxiv.org/abs/2106.09685

随着预训练的模型规模不断扩大，对所有模型参数进行全量微调（full fine-tuning）不可行。

冻结预训练模型的权重，并在 Transformer 架构的每一层中注入可训练的低秩分解矩阵，

从而大幅减少下游任务所需的可训练参数数量。

LoRALayer 求更新的变化值。 A = [ in, rank] B = [ rank, out ]

import torch.nn as nn

class LoRALayer(nn.Module):
    def __init__(self, in_dim, out_dim, rank, alpha):
        super().__init__()
        std_dev = 1 / torch.sqrt(torch.tensor(rank).float())
        self.A = nn.Parameter(torch.randn(in_dim, rank) * std_dev)
        self.B = nn.Parameter(torch.zeros(rank, out_dim))
        self.alpha = alpha

    def forward(self, x):
        x = self.alpha * (x @ self.A @ self.B)
        return x

线性层 + LoRA 层，参数更新

class LinearWithLoRA(nn.Module):

    def __init__(self, linear, rank, alpha):
        super().__init__()
        self.linear = linear
        self.lora = LoRALayer(
            linear.in_features, linear.out_features, rank, alpha
        )

    def forward(self, x):
        return self.linear(x) + self.lora(x)

3. 数的精度 -- 混合精度 + 量化操作

浮点数 -- 双精度: FP64 单精度: FP32 半精度: FP16

通过 exp和fraction 不同的范围与精度。

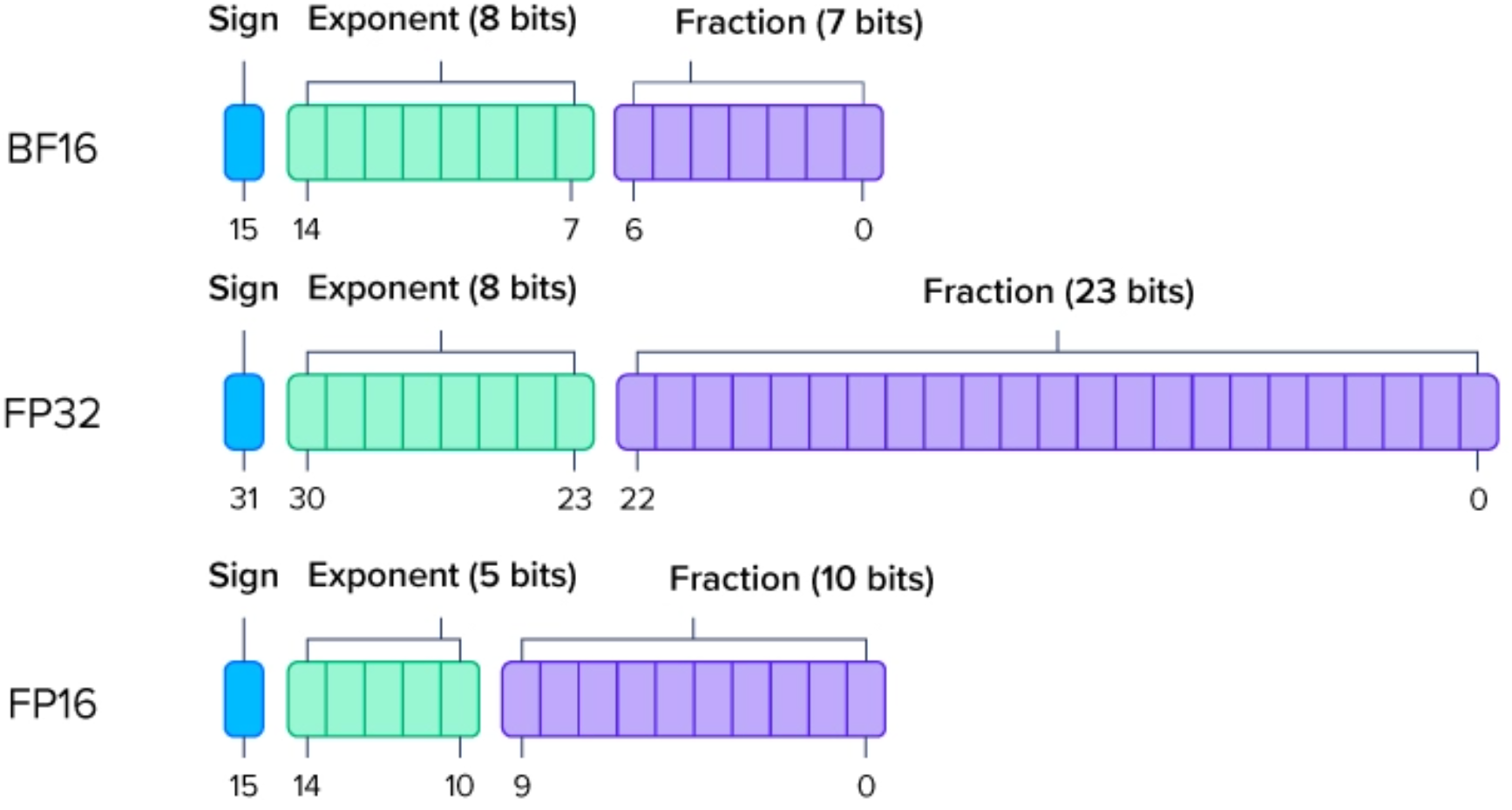
混合精度 是指在模型训练过程中，同时使用不同数值精度的格式。

量化 是指将模型中的浮点参数（如 FP32）转换为低比特整数 （如 INT8、INT4，甚至 INT2/INT1）或定点数**，** 通过减少每个参数的存储位数 来压缩模型**。**

对模型训练的帮助

1. 减少内存占用

2. 加速计算速度

3. 降低能源消耗

https://njudeepengine.github.io/LLM-Blog/2025/06/29/A3-modeling-mlp/

Task1：DenseMLPWithLoRA

Dense 的 MLP 模块 ：先将 hidden_states 从 h 维上投影（up-project）到更高的 ffh 维，

再通过 gating 机制下投影（down-project）回原始维度。

一、任务背景

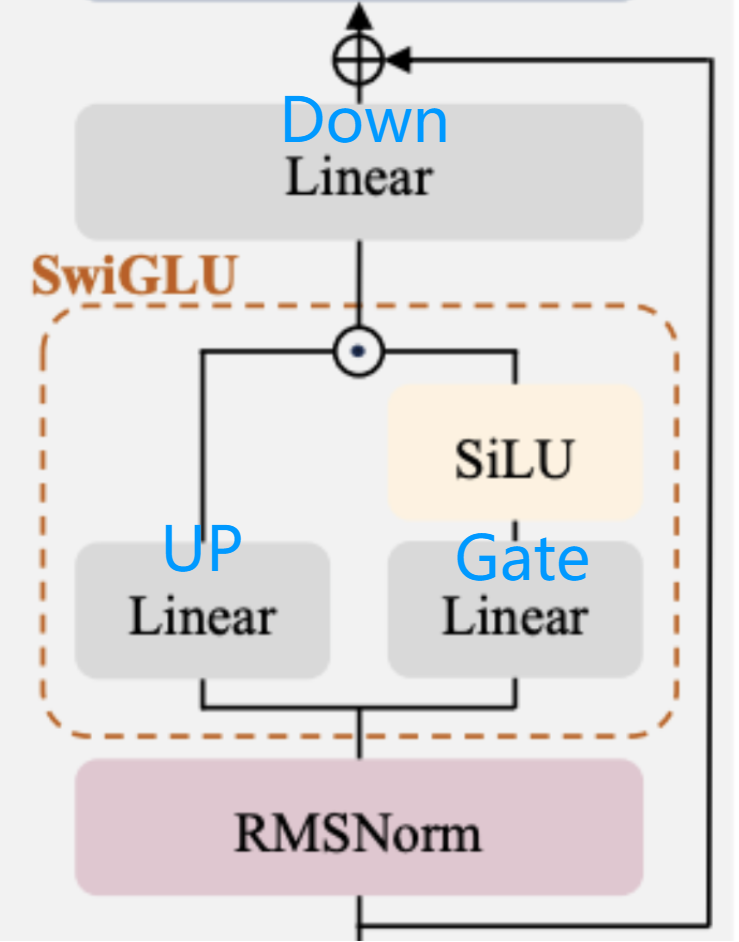
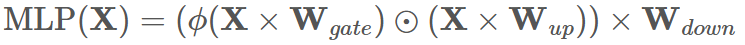
MLP 模块中的参数通常占据了 LLMs 中超过 90% 的可训练参数，

因此采用全量线性参数监督微调（supervised fine-tuning, SFT）的方式效率非常低。

LoRA 的核心基本假设是：δ W 是一个低秩且稀疏的矩阵，其可以通过低秩分解表示为：

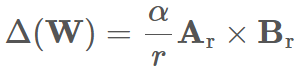
二、任务要求

对三个投影矩阵 W 进行初始化，初始化方式为从正态分布中采样。

• 如果 activation_type 使用 MLPActivationType.SIGMOID 或 MLPActivationType.BILINEAR，则使用 Xavier Initialization；
• 否则，对于其余 ReLU-family 的激活函数，则使用 Kaiming Initialization；
• 标准差 std = sqrt ( 2/ fan_in )

LoRA 低秩分解矩阵 A、B初始化：均匀分布 seed = lora_init_base_seed +1 / +2

对 lora_gate\up\down_A\B 的 seed 分别设置 offset 偏移量。

1. 若 lora_rank = 0，你应跳过任何与 LoRA 有关的逻辑

2. 参数 lora_alpha 是一个正缩放因子，默认为 None 时，表示应设置 = lora_rank（不缩放）

3. Dropout 层有 lora_dropout_seed 和 lora_dropout_rate 参数

Task2：Sparse MLP

类似多头注意力，将投影矩阵的 ffh 维度划分为 ne 个大小相等的 shard（分片）对应一个专家。

hidden states 的每个 token 通过一个机制，映射到对应的 k 个 experts。

最终，每个 token 的最终输出是来自这 k 个 experts 子输出的加权和。

从而：降低高维计算开销；通过并行学习，提高潜在模式的多样性。

下文实现方式 Mixtral 方法：

1. 训练一个 (h, ne) 的网络 G；把 h 维的输入，转换为 ne 个专家分别的概率。

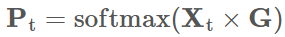
2. 只取前 k 名的 P，用 P / SUM 分配权重。将这几个 experts 的输出结果加权。

3. 每一个小专家 相当于一个 DenseMLP，调用上一问。