什么是 NumPy
NNumPy(Numerical Python)是 Python 科学计算的基础库,广泛应用于数据科学、机器学习和科学计算等领域。它由 Travis Oliphant 等人在2005年创建,是目前 Python 生态系统中最重要的数值计算工具之一。
NumPy 的核心优势和功能包括:
-
强大的 N 维数组对象(ndarray):
- 提供高效的多维数组存储和操作
- 相比 Python 原生列表,计算速度快了几个数量级
- 支持矢量化操作,避免显式循环
-
广播功能函数:
- 允许不同形状数组之间的算术运算
- 自动扩展较小数组以匹配较大数组的形状
- 例如:标量与数组的运算、不同形状数组间的运算
-
整合 C/C++ 和 Fortran 代码的工具:
- 提供 C-API 接口,可以轻松与底层高性能代码集成
- 支持调用现有的科学计算库
- 使得 Python 可以充当"胶水语言"连接不同语言的代码
-
丰富的数学函数库:
- 线性代数(矩阵运算、分解等)
- 傅里叶变换(信号处理)
- 随机数生成(蒙特卡洛模拟)
- 统计运算(均值、方差等)
NumPy 的核心是其 ndarray 对象,这是一个同构数据多维容器,具有以下重要特性:
所有元素必须是相同数据类型(dtype)
内存连续存储,访问效率高
支持各种类型的索引和切片操作
提供大量内置的数学运算方法
NumPy 的核心是其 ndarray 对象,这是一个同构数据多维容器,也就是说所有元素必须是相同类型的。
python
import numpy as np
# 创建一维数组
arr = np.array([1, 2, 3, 4, 5])
print(arr)
# 创建二维数组
arr2d = np.array([[1, 2], [3, 4], [5, 6]])
print(arr2d)
# 使用便捷函数创建数组
arr_range = np.arange(10) # 创建0到9的一维数组
arr_zeros = np.zeros((3, 4)) # 创建3行4列的零数组
arr_ones = np.ones((2, 3)) # 创建2行3列的全1数组[1 2 3 4 5]
[[1 2]
[3 4]
[5 6]]NumPy 的核心概念
数组的属性
NumPy 数组的属性提供了关于数组结构的重要信息:
ndim:- 表示数组的维度数量
- 如:一维数组ndim=1,二维数组ndim=2
- 通过
np.ndim()函数也可获取
shape:- 表示数组各维度大小的元组
- 如:形状(3,4)表示3行4列的二维数组
- 可以通过
reshape()方法改变形状
size: 数组元素的总数量- 数组元素的总数量
- 等于shape各维度大小的乘积
- 如:shape(3,4)的数组size=12
dtype: 数组元素的数据类型- 数组元素的数据类型
- 常见类型:int32,int64,float32,float64等
- 创建数组时可通过dtype参数指定
itemsize: 每个数组元素的字节大小- 每个数组元素占用的字节数
- 与dtype相关,如float64的itemsize=8
- 可以通过
nbytes属性获取数组总字节数(size*itemsize)
python
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("维度数量:", arr.ndim) # 2
print("数组形状:", arr.shape) # (2, 3)
print("元素总数:", arr.size) # 6
print("数据类型:", arr.dtype) # int64 (可能因系统而异)
print("元素字节大小:", arr.itemsize) # 8 (可能因系统而异)维度数量: 2
数组形状: (2, 3)
元素总数: 6
数据类型: int64
元素字节大小: 8数组的形状操作
在实际应用中,我们经常需要改变数组的形状以适应不同的计算需求:
reshape方法:- 不改变原数组,返回新形状的视图
- 新形状的元素总数必须与原数组相同
- 示例:将形状(6,)的数组重塑为(2,3)
resize方法:- 直接修改原数组的形状
- 可以改变元素总数,不足部分填充0
- 较少使用,通常使用reshape更安全
flatten和ravel:- 将多维数组展平为一维
- flatten返回拷贝,ravel返回视图
- 支持'C'(行优先)和'F'(列优先)两种顺序
- 转置操作:
- 通过.T属性或transpose()方法
- 交换数组的行和列
- 对于高维数组,可以指定轴顺序
- 形状操作的实际应用场景:
- 机器学习中调整输入数据的维度
- 图像处理时改变图像矩阵的形状
- 数据预处理时统一不同来源数据的形状
python
# 改变数组形状
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("原始数组:")
print(arr)
# 使用 reshape 方法改变形状(返回新数组)
reshaped_arr = arr.reshape(3, 2)
print("reshape 后的数组:")
print(reshaped_arr)
# 将多维数组展平为一维数组
flattened_c = arr.flatten(order='C') # C风格(行优先)
flattened_f = arr.flatten(order='F') # Fortran风格(列优先)
print("C风格展平:", flattened_c)
print("F风格展平:", flattened_f)原始数组:
[[1 2 3]
[4 5 6]]
reshape 后的数组:
[[1 2]
[3 4]
[5 6]]
C风格展平: [1 2 3 4 5 6]
F风格展平: [1 4 2 5 3 6]NumPy 数组的基本操作
数组索引和切片
NumPy 的索引系统非常灵活,支持多种高级索引方式:
- 基本索引:
- 与Python列表类似,使用方括号[]
- 从0开始计数,支持负索引
- 多维数组使用逗号分隔各维度索引
- 切片操作:
- 语法:start:stop:step
- 可以省略部分参数,如arr[:5]
- 会返回原数组的视图而非拷贝
- 布尔索引:
- 使用布尔数组作为索引
- 常用于条件筛选,如arr[arr>0.5]
- 返回满足条件的元素
- 花式索引(Fancy indexing):
- 使用整数数组作为索引
- 如:arr[[0,2,4]]
- 可以按特定顺序选取元素
- 多维数组索引:
- 每个维度可以独立使用上述索引方式
- 如:arr2d[1:3, [0,2]]
- 可以组合基本索引、切片、布尔索引等
python
# 一维数组索引和切片
arr1d = np.arange(10)
print("一维数组:", arr1d)
print("索引为2的元素:", arr1d[2])
print("索引2到7,步长为2:", arr1d[2:7:2])
print("索引2之后的所有元素:", arr1d[2:])
# 二维数组索引和切片
arr2d = np.arange(24).reshape(4, 6)
print("二维数组:")
print(arr2d)
print("第2行:", arr2d[1]) # 取一行
print("第2、3行:", arr2d[1:3]) # 取连续多行
print("第1、3、4行:", arr2d[[0, 2, 3]]) # 取不连续多行
print("第2列:", arr2d[:, 1]) # 取一列
print("第2、4、5列:", arr2d[:, [1, 3, 4]]) # 取不连续多列一维数组: [0 1 2 3 4 5 6 7 8 9]
索引为2的元素: 2
索引2到7,步长为2: [2 4 6]
索引2之后的所有元素: [2 3 4 5 6 7 8 9]
二维数组:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
第2行: [ 6 7 8 9 10 11]
第2、3行: [[ 6 7 8 9 10 11]
[12 13 14 15 16 17]]
第1、3、4行: [[ 0 1 2 3 4 5]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
第2列: [ 1 7 13 19]
第2、4、5列: [[ 1 3 4]
[ 7 9 10]
[13 15 16]
[19 21 22]]数组运算
NumPy 的运算分为以下几类:
- 算术运算:
- 加法(+)、减法(-)、乘法(*)、除法(/)
- 幂运算(**)、模运算(%)
- 支持标量与数组的运算
- 比较运算:
- 等于(==)、不等于(!=)
- 大于(>)、小于(<)等
- 返回布尔数组
- 逻辑运算:
- 逻辑与(np.logical_and)
- 逻辑或(np.logical_or)
- 逻辑非(np.logical_not)
- 数学函数:
- 三角函数:sin,cos,tan等
- 指数对数:exp,log,log10等
- 取整函数:floor,ceil,round等
- 统计运算:
- sum,mean,std,var等
- 可以指定沿哪个轴计算
python
# 基本数学运算
arr = np.arange(24).reshape((6, 4))
print("原数组:")
print(arr)
print("加2:")
print(arr + 2)
print("乘2:")
print(arr * 2)
print("除以2:")
print(arr / 2)
# 数组间运算
arr1 = np.arange(24).reshape((6, 4))
arr2 = np.arange(100, 124).reshape((6, 4))
print("两数组相加:")
print(arr1 + arr2)
print("两数组相乘:")
print(arr1 * arr2)原数组:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
加2:
[[ 2 3 4 5]
[ 6 7 8 9]
[10 11 12 13]
[14 15 16 17]
[18 19 20 21]
[22 23 24 25]]
乘2:
[[ 0 2 4 6]
[ 8 10 12 14]
[16 18 20 22]
[24 26 28 30]
[32 34 36 38]
[40 42 44 46]]
除以2:
[[ 0. 0.5 1. 1.5]
[ 2. 2.5 3. 3.5]
[ 4. 4.5 5. 5.5]
[ 6. 6.5 7. 7.5]
[ 8. 8.5 9. 9.5]
[10. 10.5 11. 11.5]]
两数组相加:
[[100 102 104 106]
[108 110 112 114]
[116 118 120 122]
[124 126 128 130]
[132 134 136 138]
[140 142 144 146]]
两数组相乘:
[[ 0 101 204 309]
[ 416 525 636 749]
[ 864 981 1100 1221]
[1344 1469 1596 1725]
[1856 1989 2124 2261]
[2400 2541 2684 2829]]- 广播机制的实际例子
python
# 标量与数组
arr = np.array([1,2,3])
print(arr + 5) # [6,7,8]
# 不同形状数组
a = np.array([[1],[2],[3]])
b = np.array([10,20])
print(a + b) # [[11,21],[12,22],[13,23]][6 7 8]
[[11 21]
[12 22]
[13 23]]数组的添加和删除
NumPy 提供了灵活的方法来添加和删除数组元素:
python
# 添加元素
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("原始数组:")
print(arr)
# 使用 append 添加元素
appended = np.append(arr, [[7, 8, 9]], axis=0)
print("在0轴添加一行:")
print(appended)
# 使用 insert 插入元素
inserted = np.insert(arr, 1, [[11, 12, 13]], axis=0)
print("在第1行插入新行:")
print(inserted)
# 删除元素
deleted_row = np.delete(arr, 0, axis=0) # 删除第0行
deleted_col = np.delete(arr, 1, axis=1) # 删除第1列
print("删除第0行后:")
print(deleted_row)
print("删除第1列后:")
print(deleted_col)原始数组:
[[1 2 3]
[4 5 6]]
在0轴添加一行:
[[1 2 3]
[4 5 6]
[7 8 9]]
在第1行插入新行:
[[ 1 2 3]
[11 12 13]
[ 4 5 6]]
删除第0行后:
[[4 5 6]]
删除第1列后:
[[1 3]
[4 6]]NumPy 的高级功能
统计计算
NumPy 的统计函数广泛应用于数据分析:
- 基本统计量:
- 最大值(np.max)、最小值(np.min)
- 极差(np.ptp:max-min)
- 分位数(np.percentile)
- 中心趋势:
- 均值(np.mean)
- 中位数(np.median)
- 众数(scipy.stats.mode)
- 离散程度:
- 方差(np.var)
- 标准差(np.std)
- 平均绝对偏差(np.mean(abs(x-mean)))
- 相关性:
- 协方差(np.cov)
- 相关系数(np.corrcoef)
- 直方图:
- np.histogram
- 计算数据的分布情况
统计函数的常用参数:
- axis:指定计算轴,0为列,1为行
- keepdims:是否保持维度
- dtype:指定计算数据类型
python
scores = np.array([[80, 88], [82, 81], [75, 81]])
print("成绩数组:")
print(scores)
# 最值计算
print("最大值:", np.max(scores))
print("每列的最大值:", np.max(scores, axis=0))
print("最小值:", np.min(scores))
print("每列的最小值:", np.min(scores, axis=0))
# 平均值和其他统计量
print("平均值:", np.mean(scores))
print("每列的平均值:", np.mean(scores, axis=0))
print("标准差:", np.std(scores, axis=0))
print("极值差:", np.ptp(scores, axis=0)) # 最大值与最小值之差
# 累积运算
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("累积求和(axis=0):")
print(arr.cumsum(axis=0))
print("累积求和(axis=1):")
print(arr.cumsum(axis=1))成绩数组:
[[80 88]
[82 81]
[75 81]]
最大值: 88
每列的最大值: [82 88]
最小值: 75
每列的最小值: [75 81]
平均值: 81.16666666666667
每列的平均值: [79. 83.33333333]
标准差: [2.94392029 3.29983165]
极值差: [7 7]
累积求和(axis=0):
[[1 2 3]
[5 7 9]]
累积求和(axis=1):
[[ 1 3 6]
[ 4 9 15]]数组的拼接和分割
NumPy 提供了多种数组拼接和分割的方法:
python
# 数组拼接
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
# concatenate 拼接
concat_0 = np.concatenate((a, b), axis=0) # 沿0轴拼接
concat_1 = np.concatenate((a, b), axis=1) # 沿1轴拼接
print("沿0轴拼接:")
print(concat_0)
print("沿1轴拼接:")
print(concat_1)
# stack 堆叠
stack_0 = np.stack((a, b), axis=0)
stack_1 = np.stack((a, b), axis=1)
print("沿0轴堆叠:")
print(stack_0)
print("沿1轴堆叠:")
print(stack_1)
# 特殊拼接函数
v1 = [[0, 1, 2], [3, 4, 5]]
v2 = [[6, 7, 8], [9, 10, 11]]
vstacked = np.vstack((v1, v2)) # 垂直拼接
hstacked = np.hstack((v1, v2)) # 水平拼接
print("垂直拼接:")
print(vstacked)
print("水平拼接:")
print(hstacked)
# 数组分割
arr = np.arange(9).reshape(3, 3)
splitted = np.split(arr, 3) # 分割为3部分
print("分割后的数组:")
print(splitted)沿0轴拼接:
[[1 2]
[3 4]
[5 6]
[7 8]]
沿1轴拼接:
[[1 2 5 6]
[3 4 7 8]]
沿0轴堆叠:
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
沿1轴堆叠:
[[[1 2]
[5 6]]
[[3 4]
[7 8]]]
垂直拼接:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
水平拼接:
[[ 0 1 2 6 7 8]
[ 3 4 5 9 10 11]]
分割后的数组:
[array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]NumPy 在实际项目中的应用
NumPy 在许多实际场景中都有广泛应用:
数据预处理
python
# 数据标准化
data = np.random.rand(100, 5) * 100 # 生成一些模拟数据
normalized_data = (data - np.mean(data, axis=0)) / np.std(data, axis=0)
print("原始数据均值:", np.mean(data, axis=0))
print("标准化后数据均值:", np.mean(normalized_data, axis=0)) # 应该接近0原始数据均值: [51.07820489 51.00413079 49.84528218 51.56121696 50.59229218]
标准化后数据均值: [ 2.22044605e-17 -7.99360578e-17 5.56221735e-16 7.66053887e-16
1.93178806e-16]图像处理
python
# 模拟图像处理(灰度图反转)
image = np.random.randint(0, 256, (100, 100)) # 模拟100x100的灰度图像
inverted_image = 255 - image # 图像反转
print("原图像范围:", np.min(image), "-", np.max(image))
print("反转图像范围:", np.min(inverted_image), "-", np.max(inverted_image))原图像范围: 0 - 255
反转图像范围: 0 - 255金融数据分析
python
# 计算收益率
prices = np.array([100, 102, 98, 105, 110, 108, 112])
returns = (prices[1:] - prices[:-1]) / prices[:-1]
print("价格序列:", prices)
print("收益率:", returns)
print("平均收益率:", np.mean(returns))价格序列: [100 102 98 105 110 108 112]
收益率: [ 0.02 -0.03921569 0.07142857 0.04761905 -0.01818182 0.03703704]
平均收益率: 0.019781191938054683有趣的案例:白骨精抓唐僧
为了更好地展示 NumPy 在实际问题中的应用,我们来看一个有趣的案例------"白骨精抓唐僧"。
在这个案例中,我们将模拟一个随机行走问题。假设唐僧在一片区域内移动,而白骨精需要找到他。我们可以使用 NumPy 来模拟这个过程:
python
import numpy as np
# 设置步数
steps = 200
# 生成随机行走步骤 (-1 或 1)
# 第一行代表行走方向,第二行代表方向类型(水平或垂直)
draws = np.random.choice([-1, 1], (2, steps))
# 模拟行走过程并检测何时超出搜索范围
for i in range(steps):
# 水平方向移动
condition_hor = draws[1][:i] > 0
hor = draws[0][:i][condition_hor]
hor_sum = np.sum(hor)
# 垂直方向移动
condition_ver = draws[1][:i] < 0
ver = draws[0][:i][condition_ver]
ver_sum = np.sum(ver)
# 计算当前位置到起点的距离(半径)
radius = np.sqrt(hor_sum ** 2 + ver_sum ** 2)
# 如果超出搜索范围(半径大于10),则停止搜索
if radius > 10:
print(f"出圈了,当前是第{i}步,距离起点{radius}")
break出圈了,当前是第33步,距离起点10.44030650891055这个例子展示了 NumPy 在模拟和解决实际问题中的应用:
- 使用
np.random.choice()生成随机行走路径 - 利用布尔索引筛选不同方向的移动
- 使用
np.sum()计算累积位移 - 结合数学函数
np.sqrt()计算欧几里得距离
这类随机行走模拟在金融、物理、生物等领域都有广泛应用,比如模拟股票价格变动、分子运动轨迹等。
为了更直观地展示这个过程,我们还可以使用 matplotlib 库来可视化唐僧的移动路径:
python
import matplotlib.pyplot as plt
# 设置中文字体
import matplotlib.font_manager
chinese_fonts = [f.name for f in matplotlib.font_manager.fontManager.ttflist
if 'Sim' in f.name or 'Kai' in f.name or 'Fang' in f.name]
print(chinese_fonts)
# 使用找到的中文字体
plt.rcParams['font.sans-serif'] = chinese_fonts
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 生成随机行走步骤
steps = 200
draws = np.random.choice([-1, 1], (2, steps))
# 存储路径坐标
x_positions = [0] # 初始x位置
y_positions = [0] # 初始y位置
current_x, current_y = 0, 0
# 模拟行走过程
for i in range(steps):
# 根据方向类型更新位置
if draws[1][i] > 0: # 水平方向移动
current_x += draws[0][i]
else: # 垂直方向移动
current_y += draws[0][i]
# 记录当前位置
x_positions.append(current_x)
y_positions.append(current_y)
# 计算当前位置到起点的距离
radius = np.sqrt(current_x ** 2 + current_y ** 2)
# 如果超出搜索范围(半径大于10),则停止搜索
if radius > 10:
print(f"出圈了,当前是第{i+1}步,距离起点{radius:.2f}")
break
# 绘制路径图
plt.figure(figsize=(10, 8))
plt.plot(x_positions, y_positions, 'b-', linewidth=1, alpha=0.7, label='唐僧的移动路径')
plt.plot(0, 0, 'go', markersize=10, label='起点(白骨精的位置)')
plt.plot(x_positions[-1], y_positions[-1], 'ro', markersize=10, label='唐僧最终位置')
# 绘制搜索范围圆
circle = plt.Circle((0, 0), 10, color='r', fill=False, linestyle='--', linewidth=2)
plt.gca().add_patch(circle)
plt.xlim(-15, 15)
plt.ylim(-15, 15)
plt.grid(True, alpha=0.3)
plt.xlabel('X 坐标')
plt.ylabel('Y 坐标')
plt.title('白骨精抓唐僧路径可视化')
plt.legend()
plt.show()['Kai', 'PingFang HK', 'Kaiti SC', 'Kailasa', 'SimSong', 'BiauKaiHK', 'Noto Sans Kaithi', 'STFangsong']
出圈了,当前是第84步,距离起点10.30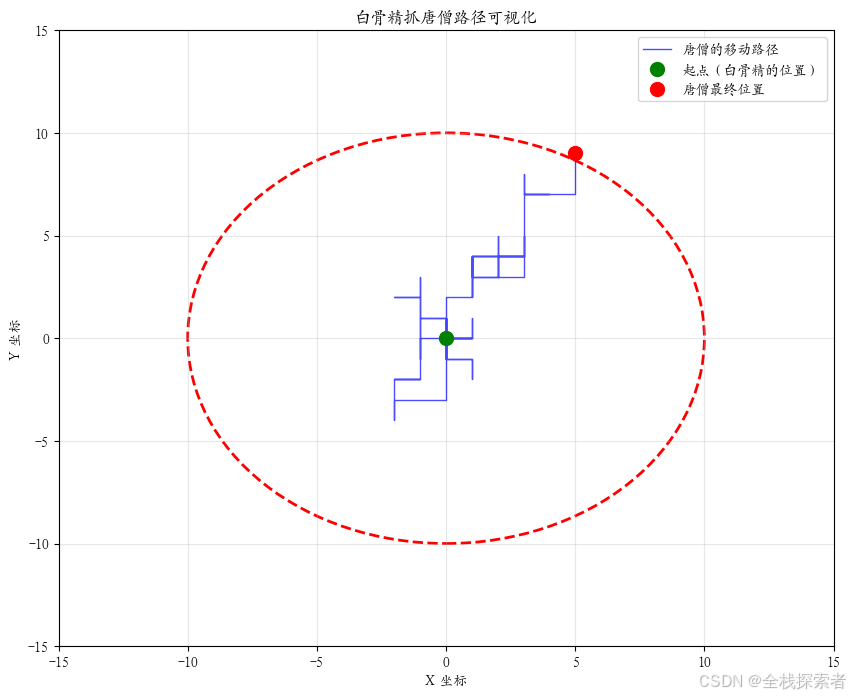
总结
NumPy 是 Python 科学计算生态系统的核心组件,它的优势包括:
- 高性能:底层由 C 实现,运算速度快
- 简洁语法:向量化操作使代码更简洁易读
- 丰富功能:提供大量数学、统计和逻辑函数
- 良好集成:与其他科学计算库(如 Pandas、Scikit-learn)无缝集成
掌握 NumPy 不仅能提高编程效率,还能为后续学习机器学习、深度学习等高级领域打下坚实基础。通过本文介绍的基本操作和高级功能,相信你已经对 NumPy 有了全面的认识,可以在实际项目中灵活运用了。
继续深入学习 NumPy,你会发现更多强大而有趣的功能,它们将在你的数据科学之旅中发挥重要作用。