插入排序：扑克牌式的排序算法！

[3.1 时间复杂度](#3.1 时间复杂度)

[3.2 稳定性](#3.2 稳定性)

[四. 结语](#四. 结语)

一.引言

想象一下你正在整理手中的扑克牌：你总是拿起下一张牌，然后将它插入到左手边已经整理好的牌堆中的正确位置。插入排序的工作原理与此如出一辙。它将一个数组（或列表）分为"已排序"和"未排序"两个部分，然后逐一将未排序部分的元素插入到已排序部分的正确位置。

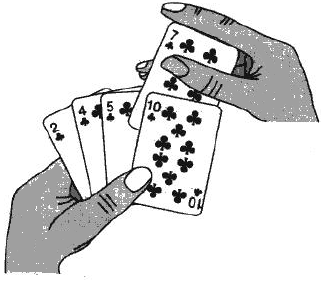
插入排序 因其简洁性、稳定性 ，以及在处理小规模或"几乎有序"数据 时所展现出的高效率，而在实际应用中占据着一席之地。

二.核心思想

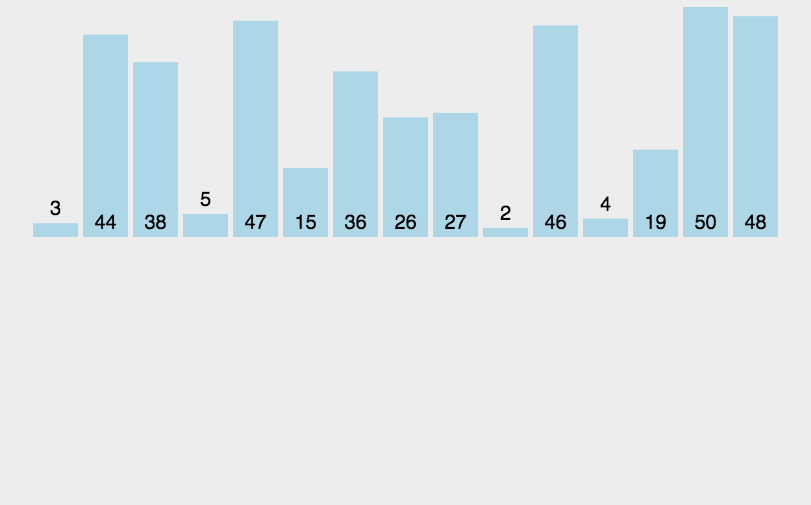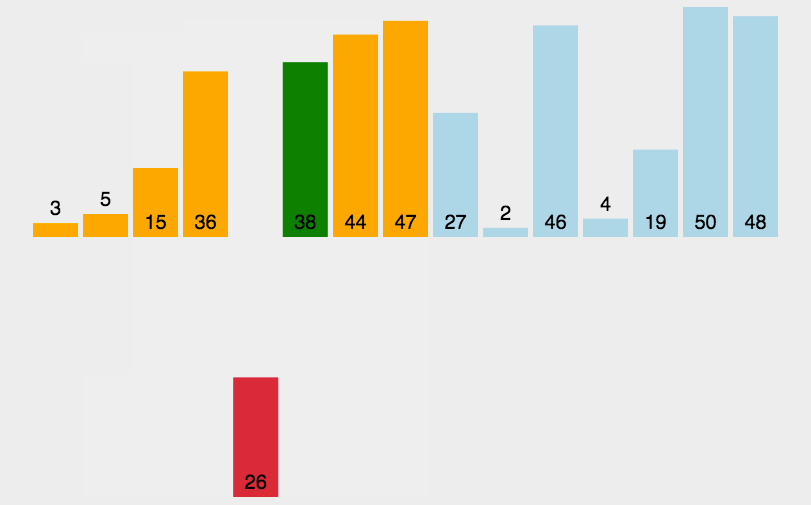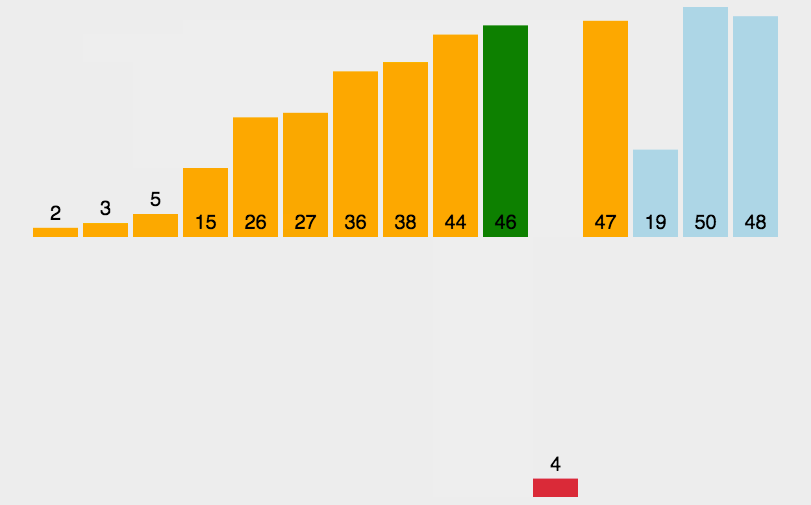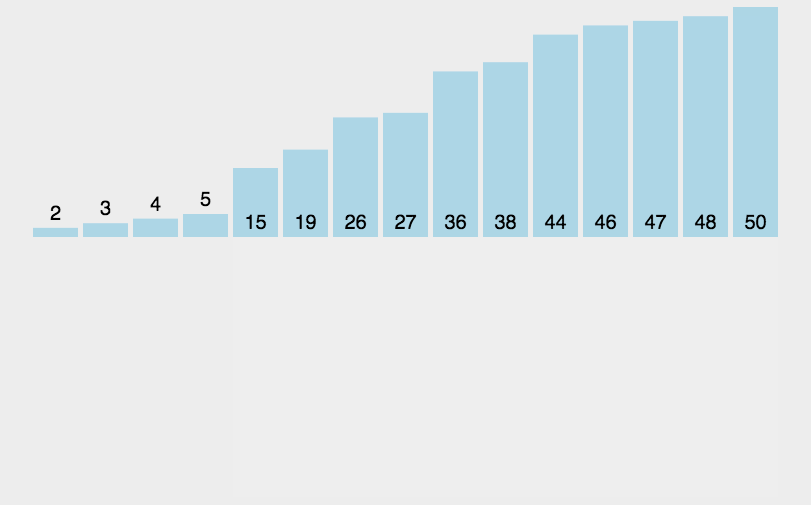
插入排序的核心在于原地构建有序序列，空间复杂度为O（1）。它从第二个元素开始，将其视为待插入的"键"（tmp），然后将这个"键"与前面已排序的序列中的元素逐一比较，如果比它大，就向后移动一位，直到找到一个小于或等于"键"的元素的位置，然后将"键"插入到该位置。

cpp 复制代码

void InsertSort(int* arr, int n)
{
	// 外层循环：遍历未排序部分的第一个元素
	// i < n - 1 是因为我们将 arr[i+1] 作为待插入元素
	for (int i = 0; i < n - 1; i++)
	{
		int end = i; // end 指向已排序序列的最后一个元素的下标
		int tmp = arr[end + 1]; // tmp 是待插入的"键"

		// 内层循环：在已排序序列中寻找 tmp 的合适位置
		while (end >= 0)
		{
			// 如果已排序元素 arr[end] 大于待插入的 tmp
			if (tmp < arr[end])
			{
				// 将 arr[end] 向后移动一位，为 tmp 腾出空间
				arr[end + 1] = arr[end];
				end--; // 继续向前比较
			}
			else
			{
				// 找到了一个小于或等于 tmp 的元素，停止比较
				break;
			}
		}
		// 将 tmp 插入到找到的正确位置（即 end + 1 的位置）
		arr[end + 1] = tmp;
	}
}

三.性能分析

3.1 时间复杂度

插入排序的性能表现高度依赖于输入数据的初始状态，其时间复杂度可以从线性到平方级变化。

最好情况O(N)： 当数组已经完全有序 时，插入排序达到它的最佳性能。在这种情况下，外循环每次迭代时，待插入的元素（tmp）只需与已排序序列的最后一个元素进行一次比较，内循环会立即终止。因此，总的操作次数与数组元素数量成线性关系。

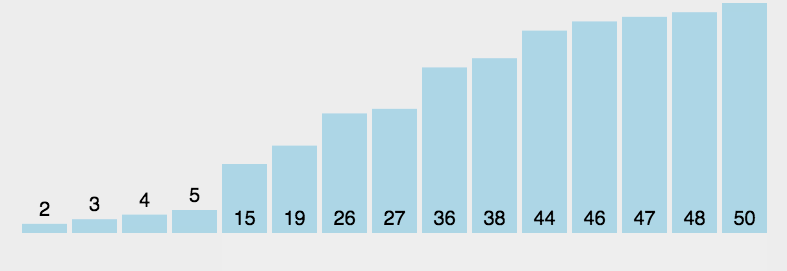
最坏情况O(N²)： 当数组完全逆序 时，算法性能最差。在这种情况下：①要插入第个元素时，它必须与前面已排序的个元素全部进行比较 ，并且全部进行移动（或交换），才能到达它最终的位置。②外循环从第二个元素开始（到），所以需要进行的比较总数大约是：

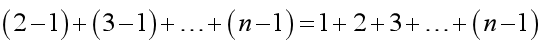
这是一个等差数列求和公式：

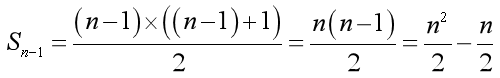
根据大 O 的渐进表示法（只保留最高次项，并忽略常数系数）：

平均情况 O(N²)： 在随机排列的数组中，平均而言，待插入的元素需要移动大约一半的已排序元素。因此，平均情况的时间复杂度与最坏情况相似，也是O(N²)。

总结： 插入排序在处理小规模数据或接近有序 的数据集时表现出色，但在处理大规模且完全无序的数据时，其二次方的时间复杂度 O(N²) 会使其效率低于其他高效排序算法。

3.2 稳定性

稳定性 是指如果一个数组中有两个或多个具有相同键值（Key）的元素，在排序后，它们在原数组中的相对顺序不会改变。

例如，有一个数组 [5a, 3, 5b]，其中 5a 和 5b 的值相同，但 5a 在 5b 的前面。
如果排序后的结果是 [3, 5a, 5b]，则该算法是稳定的。
如果排序后的结果是 [3, 5b, 5a]，则该算法是不稳定的。

**那稳定性有什么用呢？**似乎相同的值在前在后对整体排序结果并没有影响。的确对于整数进行排序确实没有影响，但是对于结构体排序，稳定性就显得至关重要了。

cpp 复制代码

struct Product {
    float price;     // 主要排序键：价格
    int relevance;   // 次要排序键：产品相关性评分（越高越好）
    // ... 其他信息（名称、销量等）
};

用户想实现这样的排序需求：首先按照价格（price）升序排列，如果价格相同，则按照相关性评分（relevance）降序排列。

|------|---------|---------|------|
| 产品ID | 价格（key） | 相关性（次序） | 原始顺序 |
| A | 100 | 95 | 1 |
| B | 200 | 80 | 2 |
| C | 100 | 70 | 3 |

第一次排序（按次要键）： 先按相关性降序排序。

|----|-------|-------|-------|
| 结果 | A（95） | B（80） | C（70） |

（和仍然保持了在前面的原始顺序）

第二次排序（按主要键）： 按价格升序排序。

价格为 100 的元素是 和。
稳定排序算法会确保在处理价格相同的元素时，它们之间已经建立好的"相关性降序"顺序不被破坏。

|------|-----|-----|-----------|----------|
| 产品ID | 价格 | 相关性 | 第一次排序后的顺序 | 最终稳定排序结果 |
| A | 100 | 95 | 1 | 1 |
| C | 100 | 70 | 3 | 2 |
| B | 200 | 80 | 2 | 3 |

如果第二次排序使用的是不稳定 算法，那么在对和进行排序时，它可能会错误地交换 和的相对位置，导致最终结果中价格相同的跑到了的前面，破坏了按相关性预先建立好的次序。

根据以上总结，由于插入排序在遇到相等的元素 时，会停止向前移动 ，并将待插入元素放置在原先那个相等元素的右侧，因此它保持了相等元素的相对顺序 。所以，插入排序是稳定的。

四. 结语

插入排序以其优雅和直观性，在众多排序算法中占有一席之地。尽管在实际中并不会直接应用插入排序来解决复杂排序问题，但凭借其在处理小规模数据或接近有序的数据集时表现出色的特点，往往作为更复杂排序算法（如快速排序、归并排序）的辅助算法。

笔者最近会快快更新完其他排序算法的！！！