NumPy 2.x 完全指南【四十二】线性代数之向量运算

文章目录

• [1. 基础知识](#1. 基础知识)
• • [1.1 什么是向量](#1.1 什么是向量)
  • [1.2 表示方法](#1.2 表示方法)
• [2. 向量运算](#2. 向量运算)
• • [2.1 加法](#2.1 加法)
  • [2.2 减法](#2.2 减法)
  • [2.3 数乘](#2.3 数乘)
  • [2.4 点积](#2.4 点积)
  • • [2.4.1 numpy.inner](#2.4.1 numpy.inner)
    • [2.4.2 numpy.vdot](#2.4.2 numpy.vdot)
    • [2.4.3 numpy.vcdot](#2.4.3 numpy.vcdot)
    • [2.4.4 numpy.linalg.vecdot](#2.4.4 numpy.linalg.vecdot)
  • [2.5 外积](#2.5 外积)
  • • [2.5.1 numpy.outer](#2.5.1 numpy.outer)
    • [2.5.2 numpy.linalg.outer](#2.5.2 numpy.linalg.outer)
    • [2.5.3 numpy.linalg.cross](#2.5.3 numpy.linalg.cross)

1. 基础知识

1.1 什么是向量

Vector \[ˈvektər] 作为名词时翻译为矢量、向量。

定义： 既有大小又有方向的量。

你稚嫩的初二已经是多少年前了？一道简单的初中物理受力分析的经典题（你还会做吗）：

向量最初应用于物理学，被称为矢量 。在初二物理的力学中，我们会学到力、弹力、重力、摩擦力、浮力，力是物体对物体的作用，国际单位制中力的单位是牛顿简称牛，用 N 表示，大小、方向、和作用点是力的三要素。力具有大小和方向，因此它是一种矢量，除了力之外，速度、加速度、位移、冲量、动量、电场强度、磁感应强度等，都是物理学中的矢量。

在数学中向量是重要和基本的概念之一，既是代数研究对象，也是几何研究对象，是沟通几何与代数的桥梁。一般在高二数学中，会学习平面向量（二维空间）或者空间向量（三维空间），在数学教材中的定义是，把既有大小又有方向的量叫做向量，只有大小没有方向的量称为数量。

1.2 表示方法

向量可以用有向线段来表示，有向线段的长度表示向量的大小，方向表示向量的方向：

印刷一般使用黑体的小写英文字母（a 、b 、c等）来表示，书写时使用字母加上箭头（→）表示：

A B ⃗ 、 a ⃗ 、 b ⃗ 、 c ⃗ \vec{AB}、\vec{a}、\vec{b}、\vec{c} AB 、a 、b 、c

向量的大小称为向量的长度(或称模)，记作：

∣ A B ∣ ⃗ 、 ∣ a ∣ ⃗ 、 ∣ b ∣ ⃗ 、 ∣ c ∣ ⃗ \vec{|AB|}、\vec{|a|}、\vec{|b|}、\vec{|c|} ∣AB∣ 、∣a∣ 、∣b∣ 、∣c∣

向量根据不同的特征可以分为很多种，比如，根据长度(模)可分为：

• 零向量：长度(模) 为 0 的向量
• 单位向量：长度等于 1 个单位长度的向量

根据维度的不同，可以分为：

• 平面向量：二维平面上的向量
• 空间向量：三维空间中的向量
• N维向量：具有 N 个分量的向量

在平面直角坐标系中，平面向量的表示方法是通过坐标轴的分量来定义的，例如，向量 v 记作：

v ⃗ = ( x , y ) \vec{v}=(x,y) v =(x,y)

其中，x 是向量在 X 轴上的分量，y 是向量在 Y 轴上的分量。起点通常是原点（0,0），终点为（x，y），方向从原点指向终点，例如，向量（4,3）表示为：

同理，空间向量向量 v 记作：

v ⃗ = ( x , y , z ) \vec{v}=(x,y,z) v =(x,y,z)

在空间直角坐标系中，向量（3,4,5）表示为：

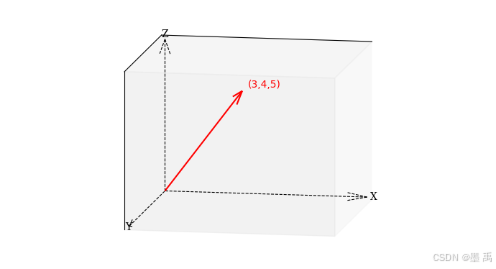
N 维向量是平面和空间向量概念的推广，高维空间无法直观可视化，所以比较抽象，记作：

v ⃗ = ( x 1 , x 2 , ... , x n ) \vec{v}=(x_1, x_2, \dots, x_n) v =(x1,x2,...,xn)

在 NumPy 中，向量通常用一维数组（1D array）来表示，其 shape 形如 (n,)，示例：

# 1. 创建平面向量 (2D 向量)
# 创建一个二维向量 [x, y]
plane_vector = np.array([3, 4])

# 2. 创建空间向量 (3D 向量)
# 创建一个三维向量 [x, y, z]
space_vector = np.array([1, 2, 3])

# 3. 创建 N 维向量
# # 从列表创建自定义向量
n_dim_vector_custom = np.array([1, 4, 9, 16, 25, 36, 49])

2. 向量运算

向量之间常见的运算有：

• 加法
• 减法
• 数乘
• 向量之间的乘法：
  • 数量积
  • 向量积

2.1 加法

在初中学物理时，力作为一种矢量，加减运算遵循平行四边形法则或三角形法则，例如，平行四边形法则中，两个共点力的合力大小和方向，可通过以这两个力为邻边作平行四边形确定，对角线就代表合力的大小和方向：

数学中的向量加法运算也是一样的，例如，使用三角形法则，向量（1,3）加上向量（3,2）的几何表示：

从图中很直观的就能看出，‌向量加法‌的规则是按照分量逐一相加，设 a 向量为：

a ⃗ = ( x 1 , y 1 ) \vec{a}=(x_1,y_1) a =(x1,y1)

设 b 向量为：

b ⃗ = ( x 2 , y 2 ) \vec{b}=(x_2,y_2) b =(x2,y2)

则它们的和为：

a ⃗ + b ⃗ = ( x 1 + x 2 , y 1 + y 2 ) \vec{a}+\vec{b}=(x_1+x_2,y_1+y_2) a +b =(x1+x2,y1+y2)

以此类推，空间及更高维度的向量也遵循这样的加法规则。

在 Python 中，可以使用列表（List）或者元组（Tuple）表示向量：

a = [1, 2, 3] # List
a = (1, 2, 3) # Tuple

定义两个向量然后直接相加，可以看到 Python 中，a + b 实际上是将列表 a 和列表 b 合并成一个新的列表，而不是对列表中的元素进行向量运算：

# 定义向量
a = [1, 2, 3]
b = [4, 5, 6]
# 期望结果：[5, 7, 9]
# 实际输出 [1, 2, 3, 4, 5, 6]
print(a + b)

需要使用列表推导式、 zip 函数来实现：

# 向量加法（列表推导式）
addition_result = [a + b for a, b in zip(a, b)]
print(addition_result)

在 NumPy 中，向量通常用一维数组表示。进行向量加法时，最直接的方法是使用 + 运算符或 np.add() 函数。这两种方法都会对两个向量的对应元素进行相加（逐元素加法）。

示例：

# 创建两个向量
vector1 = np.array([1, 2, 3])
vector2 = np.array([4, 5, 6])

# 方法1: 使用 + 运算符
result1 = vector1 + vector2
print("使用 + 运算符:", result1)  # 输出: [5 7 9]

# 方法2: 使用 np.add() 函数
result2 = np.add(vector1, vector2)
print("使用 np.add() 函数:", result2)  # 输出: [5 7 9]

2.2 减法

减法是加法的逆运算，所以向量的减法，只要将一个向量取反，然后相加即可，几何表示：

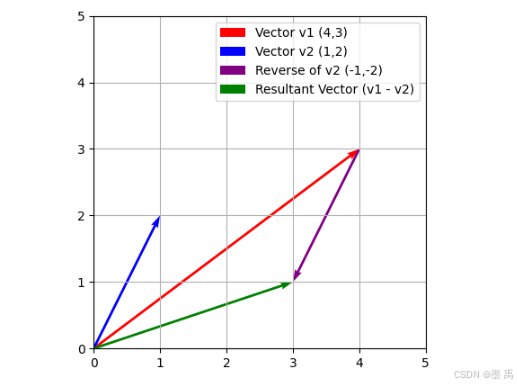
运算公式为：

a ⃗ − b ⃗ = ( x 1 − x 2 , y 1 − y 2 , . . . , x n − y n ) \vec{a}-\vec{b}=(x_1-x_2,y_1-y_2,..., xₙ − yₙ) a −b =(x1−x2,y1−y2,...,xn−yn)

在 NumPy 中实现向量减法非常直接，你主要可以使用 - 运算符或 np.subtract() 函数。它们都会对两个向量的对应元素进行相减（逐元素减法）。

示例：

# 创建两个向量
vector_a = np.array([10, 20, 30])
vector_b = np.array([5, 3, 1])

# 方法1: 使用 - 运算符
result_operator = vector_a - vector_b

# 方法2: 使用 np.subtract() 函数
result_function = np.subtract(vector_a, vector_b)

print("使用 - 运算符:", result_operator)    # 输出: [5 17 29]
print("使用 np.subtract() 函数:", result_function) # 输出: [5 17 29]

2.3 数乘

向量数乘是一个实数和一个向量有关的一种向量运算，即数量与向量的乘法运算，结果是一个向量。

设向量 a ⃗ \vec{a} a 为：
a ⃗ = ( a 1 , a 2 , a 3 , . . . , a n ) \vec{a} = (a_1, a_2, a_3, ..., a_n) a =(a1,a2,a3,...,an)

实数 λ λ λ 与向量 a ⃗ \vec{a} a 的数乘结果为：
λ a ⃗ = ( λ a 1 , λ a 2 , λ a 3 , . . . , λ a n ) \lambda \vec{a} = (\lambda a_1, \lambda a_2, \lambda a_3, ..., \lambda a_n) λa =(λa1,λa2,λa3,...,λan)

代码示例：

# 定义向量和标量
a = np.array([3, 4, -2])
lambda_val = 2

# 进行数乘运算
result = lambda_val * a
print(result)  # 输出: [ 6  8 -4]

计算过程：
λ a ⃗ = 2 × ( 3 , 4 , − 2 ) = ( 2 × 3 , 2 × 4 , 2 × ( − 2 ) ) = ( 6 , 8 , − 4 ) \lambda \vec{a} = 2 \times (3, 4, -2) = (2 \times 3, 2 \times 4, 2 \times (-2)) = (6, 8, -4) λa =2×(3,4,−2)=(2×3,2×4,2×(−2))=(6,8,−4)

2.4 点积

向量点积 是向量之间的一种基本运算，两个向量的对应分量相乘然后求和，其结果是一个标量。点积的叫法来源于其运算符号是一个点 ⋅ ，在高等数学中称之为数量积 （结果是一个数量），在线性代数中一般称之为内积。

对于两个向量 a a a 和 b b b，它们的点积坐标公式（代数法）为：
a ⃗ ⋅ b ⃗ = ( a 1 ⋅ b 1 + a 2 ⋅ b 2 + . . . + a n ⋅ b n ) = ∑ i = 1 n a i b i \vec{a}⋅\vec{b}=(a_1⋅b_1+a_2⋅b_2+...+ a_n⋅b_n)= \sum_{i=1}^{n} a_i b_i a ⋅b =(a1⋅b1+a2⋅b2+...+an⋅bn)=i=1∑naibi

NumPy 提供了多个向量点积函数：

• numpy.inner(a, b, /)
• numpy.vdot(a, b, /)
• numpy.vecdot(x1, x2, /[, out, ...])
• numpy.linalg.vecdot(x1, x2, /, *[, axis])

2.4.1 numpy.inner

计算两个数组的内积。

函数定义：

numpy.inner(a, b, /)

注意事项：

• 对于一维数组（向量），计算的是普通的内积（不涉及复数共轭），即对应元素乘积之和 。
• 对于更高维度的数组，计算的是在最后一个轴上的和积。

示例 1 ，向量的普通内积：

a = np.array([1,2,3])
b = np.array([0,1,0])

result = np.inner(a, b) # 计算结果为 (1 * 0 + 2 * 1 + 3 * 0) = 2 
print(result) # 输出 2

2.4.2 numpy.vdot

将输入数组展平为一维（始终为向量）后计算的点积。

函数定义：

numpy.vdot(a, b, /)

参数解释：

• a：如果 a 是复数，则在计算点积之前会取其复共轭。
• b：点积的第二个参数。

示例 1 ，处理多维数组（会被展平）：

a = np.array([[1, 4], [5, 6]])
b = np.array([[4, 1], [2, 2]])

# 展平后点积的手动计算: 1 * 4 + 4 * 1 + 5 * 2 + 6 * 2 = 4 + 4 + 10 + 12 = 30
result3 = np.vdot(a, b)
print(result3)  # 输出: 30

示例 2 ，复数处理：

a = np.array([1+2j, 3+4j])
b = np.array([5+6j, 7+8j])

result1 = np.vdot(a, b)
print(result1)  # 输出: (70-8j)

result2 = np.vdot(b, a)
print(result2)  # 输出: (70+8j)

2.4.3 numpy.vcdot

计算两个数组的向量点积。

函数定义：

numpy.vecdot(x1, x2, /, out=None, *, casting='same_kind', order='K', dtype=None, subok=True[, signature, axes, axis])

参数解释：

• x1, x2：输入的数组，不允许标量。输入数组的最后一个维度必须相同。
• out：可选，用于存储计算结果的数组。如果提供，其形状必须为 x1 和 x2 广播后的形状并移除最后一个轴。如果未提供或为 None，则分配一个新数组。
• **kwargs：关键字参数，请参阅 ufunc 实例的参数文档。

返回值： 输入的向量点积。仅当 x1 和 x2 都是一维向量时，结果才为标量。

和 vdot 功能相似，不同点为：

• 处理复数：如果第一个参数是复数， vdot 则会使用其复共轭。vcdot 中如果 x1 或 x2 中的某个向量是复数，则取其复共轭，否则保持不变。
• 处理多维数组：vdot 进行向量点积之前先将参数展平为一维数组。

示例 1，一维数组点积运算：

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
result = np.vecdot(a, b) # 计算: (1 * 4 + 2 * 5 + 3 * 6) = 32
print(result)  # 输出: 32

示例 2，二维数组会被视为多个向量，即每一行作为单独向量进行计算：

# 计算沿最后一个轴 (每行) 的点积
v = np.array([[0., 5., 0.],
              [0., 0., 10.],
              [0., 6., 8.]]) # 形状 (3, 3)
n = np.array([0., 0.6, 0.8]) # 形状 (3,)
result = np.vecdot(v, n) # 计算每行与 n 的点积
print(result)  # 输出: array([ 3.,  8., 10.])
# 计算过程:
# [0.*0. + 5.*0.6 + 0.*0.8] = 3.0
# [0.*0. + 0.*0.6 + 10.*0.8] = 8.0
# [0.*0. + 6.*0.6 + 8.*0.8] = 10.0

示例 3， 使用 axis 参数可以指定轴：

v = np.array([[0., 5., 0.],
              [0., 0., 10.],
              [0., 6., 8.]]) # 形状 (3, 3)
n = np.array([[0.], [0.6], [0.8]]) # 形状 (3, 1)


# 指定 axis=0 计算沿第一个轴的点积
result_axis0 = np.vecdot(v, n, axis=0) # 计算每列与 n 的点积
print(result_axis0)  # 输出: array([ 0.   4.8 12.4]
# 逐列计算点积：
# 第一列的点积:
# 取 v 的第一列: [0., 0., 0.]
# 与 n 的对应元素相乘并求和: (0. * 0.) + (0. * 0.6) + (0. * 0.8) = 0
# 第二列的点积:
# 取 v 的第二列: [5., 0., 6.]
# 计算: (5. * 0.) + (0. * 0.6) + (6. * 0.8) = 0 + 0 + 4.8 = 4.8
# 第三列的点积:
# 取 v 的第三列: [0., 10., 8.]
# 计算: (0. * 0.) + (10. * 0.6) + (8. * 0.8) = 0 + 6 + 6.4 = 12.4

2.4.4 numpy.linalg.vecdot

同 numpy.vecdot ，仅仅是包含了与数组 API 兼容的参数。

2.5 外积

向量外积 也是向量之间的一种基本运算，两个向量会按特定顺序进行分量的交叉相乘再相减，最终得到一个新向量。

在高等数学中称之为向量积 （结果是一个向量），在线性代数中一般称之为叉积（运算符号是一个 x ）或外积。

在学习线性代数时，叉积一般用于三维空间中的向量，在三维空间中，给定两个三维向量 a = (a₁, a₂, a₃) 和 b = (b₁, b₂, b₃)，它们的叉积 a × b 计算公式为：
a × b = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ = i ( a 2 b 3 − a 3 b 2 ) − j ( a 1 b 3 − a 3 b 1 ) + k ( a 1 b 2 − a 2 b 1 ) \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = \mathbf{i}(a_2b_3 - a_3b_2) - \mathbf{j}(a_1b_3 - a_3b_1) + \mathbf{k}(a_1b_2 - a_2b_1) a×b= ia1b1ja2b2ka3b3 =i(a2b3−a3b2)−j(a1b3−a3b1)+k(a1b2−a2b1)

2.5.1 numpy.outer

计算两个向量的外积。如果输入的数组不是一维的，函数会先将其展平为一维数组再进行计算。

函数定义：

numpy.outer(a, b, out=None)

输入参数：

• a：第一个输入向量。如果输入是多维数组，会被展平为一维数组 。
• b：第二个输入向量。同样，如果输入是多维数组，也会被展平为一维数组 。
• out：指定一个用于存储计算结果的数组。这是一个可选参数 。

示例 1 ，计算两个一维向量的外积：

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
result = np.outer(a, b)
print(result)
# 输出: [[ 4  5  6]
#        [ 8 10 12]
#        [12 15 18]]

示例 2 ，即使输入是多维数组，函数也会先将其展平：

a = np.array([[1, 2], [3, 4]])  # 形状 (2,2)
b = np.array([10, 20])          # 形状 (2,)
result = np.outer(a, b)
print(result)
# 数组 a 被展平为 [1, 2, 3, 4]
# 输出: [[ 10  20]
#        [ 20  40]
#        [ 30  60]
#        [ 40  80]]

2.5.2 numpy.linalg.outer

计算两个向量的外积。此函数与 Array API 兼容。与 np.outer 相比，linalg.outer 仅接受一维输入数组，是外积运算的一个严格版本。

函数定义：

linalg.outer(x1, x2, /)

输入参数：

• x1：第一个一维输入向量，长度为 M 。必须为数值数据类型。
• x2：第二个一维输入向量，长度为 N 。必须为数值数据类型。

2.5.3 numpy.linalg.cross

专门用于计算三维向量（即每个向量必须恰好有 3 个元素）叉积，符合 Array API 标准。

函数定义：

numpy.outer(a, b, out=None)

输入参数：

• a：第一个输入数组。
• b：第二个输入数组。
• axis：指定在 x1 和 x2 中，哪个轴（维度）包含了要进行叉积计算的三维向量。该轴的长度必须为 3 。默认值为 -1 ，表示最后一个轴 。

示例 1 ，计算两个三维向量的叉积：

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
result = np.linalg.cross(x, y)
print(result)  # 输出: [-3, 6, -3]

示例 2 ，当输入是二维数组时，函数会批量、逐对地计算叉积：

x = np.array([[1, 2, 3], [4, 5, 6]])  # 包含两个三维向量
y = np.array([[4, 5, 6], [1, 2, 3]])
result = np.linalg.cross(x, y)
print(result)
# 输出:
# [[-3, 6, -3],
#  [ 3, -6, 3]]

示例 3 ，通过 axis 参数可以改变定义向量的维度：

x = np.array([[1, 2], [3, 4], [5, 6]])  # 形状 (3, 2)
y = np.array([[4, 5], [6, 1], [2, 3]])
# 注意：直接使用 np.linalg.cross(x, y) 会报错，因为默认在最后一个轴（dim=2）找3元素向量，但该轴维度是2。
# 需要指定包含3元素向量的轴（此例中应为0轴，其维度是3，符合要求）
result = np.linalg.cross(x, y, axis=0)
print(result)
# 输出: 
# [[-24, 6],
#  [ 18, 24],
#  [ -6, -18]]