本篇文章主要讲解算法练习题
1 压缩字符串
题目描述:
给你一个字符数组
chars,请使用下述算法压缩:从一个空字符串
s开始。对于chars中的每组 连续重复字符 :
- 如果这一组长度为
1,则将字符追加到s中。- 否则,需要向
s追加字符,后跟这一组的长度。压缩后得到的字符串
s不应该直接返回 ,需要转储到字符数组chars中。需要注意的是,如果组长度为10或10以上,则在chars数组中会被拆分为多个字符。请在 修改完输入数组后 ,返回该数组的新长度。
你必须设计并实现一个只使用常量额外空间的算法来解决此问题。
**注意:**数组中超出返回长度的字符无关紧要,应予忽略。
示例 1:
输入:chars = ["a","a","b","b","c","c","c"] 输出:返回 6 ,输入数组的前 6 个字符应该是:["a","2","b","2","c","3"] 解释:"aa" 被 "a2" 替代。"bb" 被 "b2" 替代。"ccc" 被 "c3" 替代。示例 2:
输入:chars = ["a"] 输出:返回 1 ,输入数组的前 1 个字符应该是:["a"] 解释:唯一的组是“a”,它保持未压缩,因为它是一个字符。示例 3:
输入:chars = ["a","b","b","b","b","b","b","b","b","b","b","b","b"] 输出:返回 4 ,输入数组的前 4 个字符应该是:["a","b","1","2"]。 解释:由于字符 "a" 不重复,所以不会被压缩。"bbbbbbbbbbbb" 被 “b12” 替代。提示:
1 <= chars.length <= 2000chars[i]可以是小写英文字母、大写英文字母、数字或符号
题目解析:
这道题目会给你一个字符数组 chars,其中存放着小写、大写英文字母以及数字或者一些符号,题目要求你将数组按照下列方式压缩:如果一个字符连续个数为1,那就不用压缩;如果一个字符连续个数大于1个,比如12个,那你就需要保留一个该字符,并将后面的字符依次改为该字符连续出现的次数(注意是从最高位开始),并且返回压缩后的有效字符个数。比如 chars = [ 'a','b','b','b', 'b', 'b', 'b', 'b', 'b','b','b','b','b' ],那么该数组经过压缩后 chars = [ 'a','b','1','2', 'b', 'b', 'b', 'b', 'b', 'b','b','b','b' ],因为 'a' 只是连续出现了一次,所以不必修改,'b' 连续出现了12次,所以保留第一个 'b',将后面的两个字符改为 '1' 与 '2',最终有效字符个数就是4,所以返回 4 就可以了。
算法讲解:
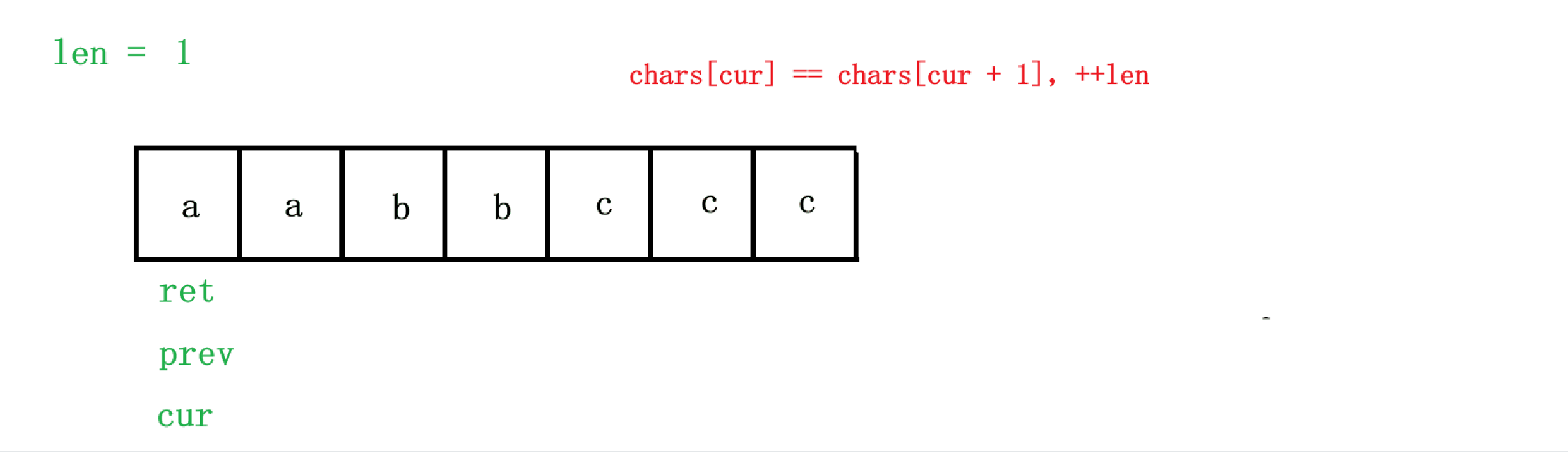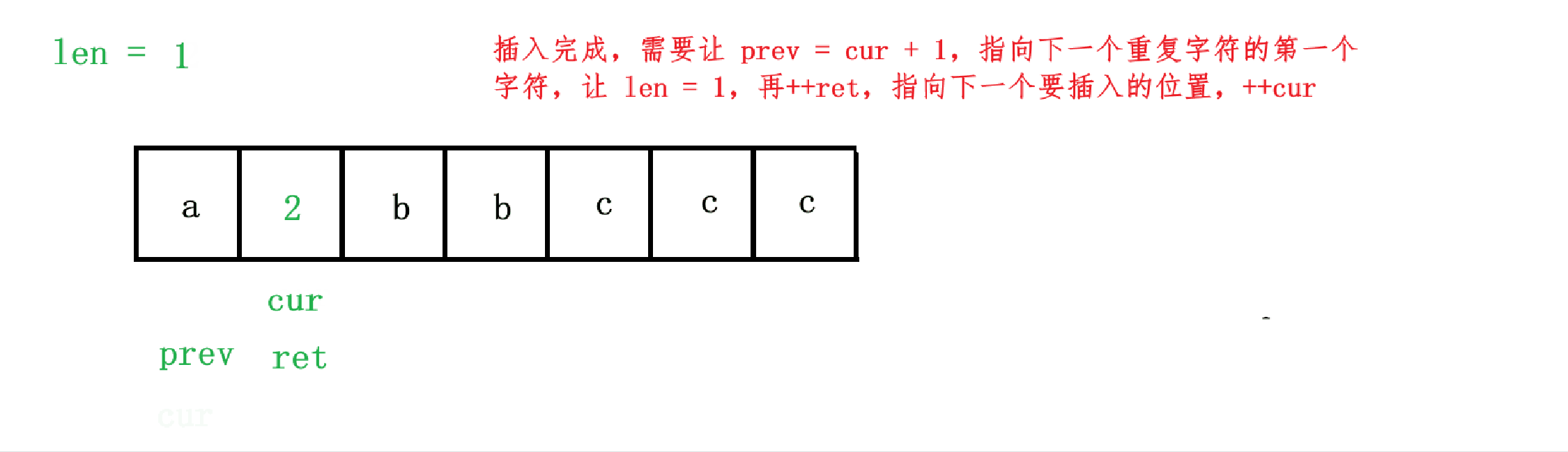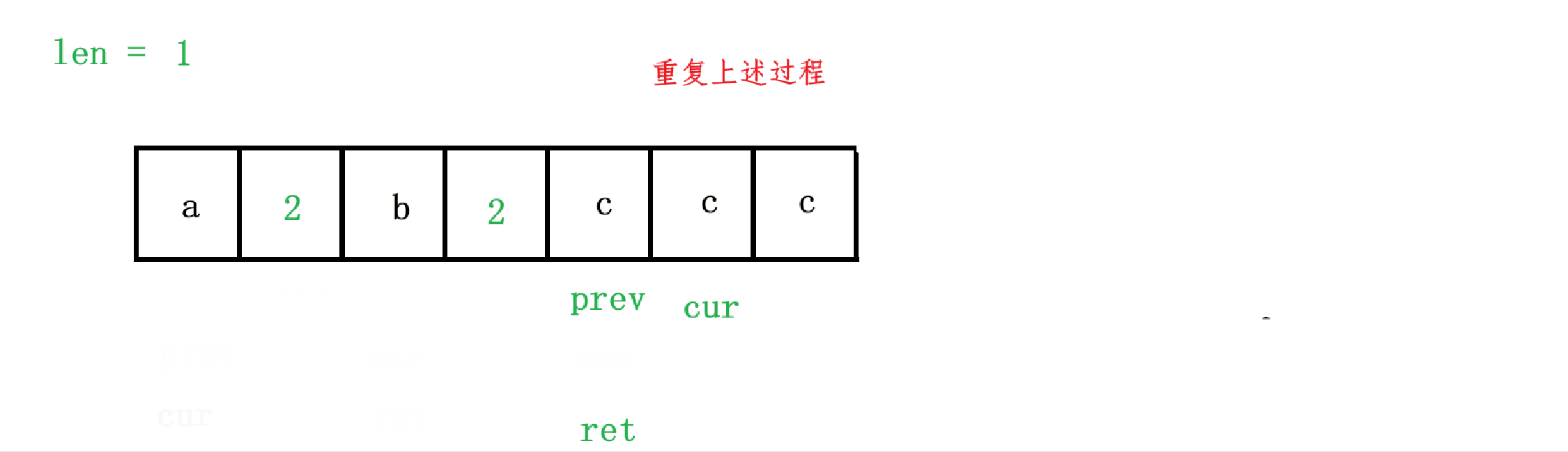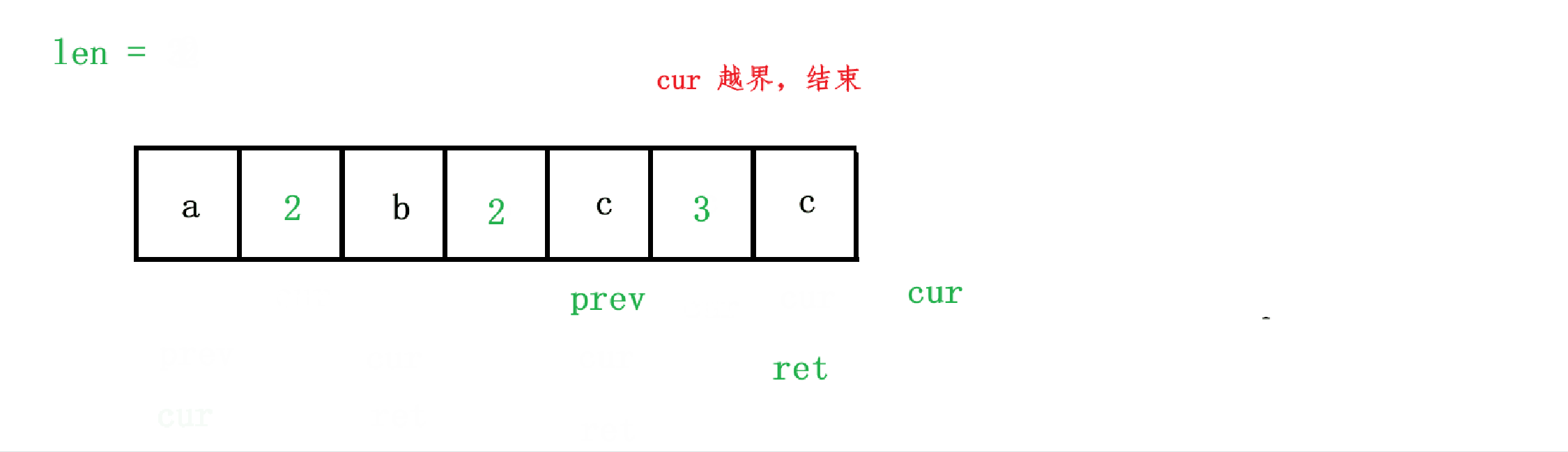
这道题目我们比较好想的就是双指针算法了。我们用一个 cur 变量来遍历数组,然后再利用 prev 变量来记录与 cur 变量相同的第一个字符,利用 len 变量来记录连续相同字符的个数,但是仅仅有 prev 与 cur 变量还不足以解决问题,因为 prev 会标记第一个与 cur 相同的字符,我们假设 chars = ['a', 'a', 'b', 'b', 'b', 'b', 'c', 'c', 'c'],当我们 prev = 6, cur = 8 时,此时 chars 已经变为 ['a', '2', 'b', '4', 'b', 'b', 'c', 'c', 'c']了,此时 prev 指向第一个 'c',cur 指向最后一个 'c',如果我们直接把 prev + 1 位置进行修改,是不符合要求的,所以我们还需要一个 ret 变量来指向要插入的下一个位置,在算法设计过程中,我们只要记住 cur 一直向前遍历,prev 指向第一个与 cur 相同的字符,ret 指向下一个要进行插入的位置,len 来记录连续相同字符的个数。
首先我们让 cur = 0,如果 chars[cur] == chars[cur + 1],那就 ++len,这里注意 len 初始值需要为1,因为连续字符个数至少为一个嘛,如果 chars[cur] != chars[cur + 1],cur 正好是最后一个连续相同的字符,所有此时连续字符个数就是1;如果 chars[cur] != chars[cur + 1] 时,cur 位于相同字符的最后一个位置,此时 len 已经记录了当前相同字符的个数,此时我们需要先让下一个位置为当前相同的字符,而 prev 正好记录着第一个与 cur 相同的字符,所以我们需要先让 chars[ret] = chars[prev],然后再让 ret 及之后的位置插入重复的字符数(如果 len > 1),也就是插入 len 的每一位,即判断 len 是否为 0,然后 chars[++ret] = len % 10 + '0',然后再让 len /= 10,这样插入完之后,其实是按照从低位到高位插入的,比如 chars = ['a','b','b','b', 'b', 'b', 'b', 'b', 'b', 'b','b','b','b' ],最后插入完其实是 ['a','b','2','1', 'b', 'b', 'b', 'b', 'b', 'b','b','b','b']的,所以我们需要反转 chars 中这两个位置,所以我们需要反转 [2, 1] 这两个位置,所以我们还需要一个变量 start 来记录要开始反转的位置,也就是刚开始让 chars[ret] = chars[prev] 的下一个位置,所以 start = ret + 1,同时插入结束之后,ret 正好指向最后一个修改的字符,但是需要注意 reverse 的迭代器区间是左闭右开的区间,所以需要 reverse(chars.begin() + start, chars.begin() + ret + 1)。
但是有一个边界情况需要注意,就是示例1,chars = ["a","a","b","b","c","c","c"] 的情况,最后字符 'c' 的情况,也就是当 cur == 6 的情况下,不仅 cur + 1 会越界,最后一个 'c' 字符也不会被添加到 ret 后面,所以最终结果是 ['a', '2', 'b', '2'],所以我们需要特殊判断一下,当 cur == chars.size() - 1 时,我们也需要将当前字符与长度插入到 chars 中。整个算法的过程如图:
代码:
cpp
class Solution
{
public:
int compress(vector<char>& chars)
{
if (chars.size() == 0) return 0;
if (chars.size() == 1) return 1;
//当前重复字符个数
int len = 1;
int ret = 0, prev = 0;
for (int cur = 0; cur < chars.size(); ++cur)
{
if (cur + 1 < chars.size() && chars[cur] == chars[cur + 1]) ++len;
else if (cur == chars.size() - 1 || chars[cur] != chars[cur + 1])
{
chars[ret] = chars[prev];
if (len > 1)
{
int start = ret + 1;
while (len)
{
chars[++ret] = (len % 10 + '0');
len /= 10;
}
//不要忘记反转
reverse(chars.begin() + start, chars.begin() + ret + 1);
}
//让 ret 指向下一个需要修改的字符
++ret;
//修改prev
prev = cur + 1;
len = 1;
}
}
return ret;
}
};2 分发饼干
题目描述:
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子
i,都有一个胃口值g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干j,都有一个尺寸s[j]。如果s[j] >= g[i],我们可以将这个饼干j分配给孩子i,这个孩子会得到满足。你的目标是满足尽可能多的孩子,并输出这个最大数值。示例 1:
输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。 虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。 所以你应该输出 1。示例 2:
输入: g = [1,2], s = [1,2,3] 输出: 2 解释: 你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。 你拥有的饼干数量和尺寸都足以让所有孩子满足。 所以你应该输出 2。提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
题目解析:
这道题目会给你两个数组 g 和 s,g[i] 代表着每个孩子的胃口,s[i] 代表着每个饼干的满足度,当饼干的满足度大于等于孩子的胃口,也就是 s[i] >= g[i] 时,该孩子会得到满足,可以随机分配饼干,每个饼干只能给一个孩子吃。题目要求你求出能够满足孩子的最大个数。例如 g = [1, 2, 3, 4],s = [1, 1, 2],返回值就是2,因为虽然有三个饼干,但是能够得到的满足的孩子个数只有两个,所以最终返回 2。
算法讲解:
我们先来想一下怎么才能使得得到满足孩子的个数最多呢?当每个饼干的满足度正好满足每个孩子的胃口时,此时满足孩子的个数是最多的,但是题目中并不会是完全相等的,所以我们就需要让满足度小的饼干去满足小胃口的孩子,最好满足度和胃口相等,这样能满足的孩子个数就是最多的,比如 g = [1, 3, 8, 4],s = [2, 2, 5, 8],我们让 s 中 2 满足度的饼干去满足 1 胃口的孩子,而不是让 8 满足度的饼干去满足 1 胃口的孩子,这样满足孩子的个数才能达到最多,否则 8 胃口的孩子就有饼干去满足了,我们就相当于白白浪费了 7 满足度,所以这道题目的思想就是用最低满足度的饼干去满足最低胃口的孩子。
为了实现这一算法,最简单的就是双指针算法 。我们需要先对两个数组排序。排完序之后,我们使用 begin1 来遍历 g,begin2 来遍历 s,如果 begin1 < g.size() && begin2 < s.size() 时,我们进入循环,如果 s[begin2] >= g[begin1],我们就 ++begin1,++begin2,++count,因为当前孩子已经被当前饼干满足了,我们需要判断下一个饼干和下一个孩子的情况,如果 s[begin2] < g[begin1],我们只需 ++begin2 即可,因为当前饼干无法满足该孩子,前面饼干的满足度都比当前饼干低,所以都无法满足该孩子,只能向后寻找更大满足的饼干来满足该孩子。最后返回 count 即可。
代码:
cpp
class Solution
{
public:
int findContentChildren(vector<int>& g, vector<int>& s)
{
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int begin1 = 0, begin2 = 0;//begin1 遍历 g,begin2 遍历s
int count = 0;
while (begin1 < g.size() && begin2 < s.size())
{
if (s[begin2] >= g[begin1])
{
++begin1;
++count;
}
++begin2;
}
return count;
}
};3 寻找峰值
题目描述:
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组
nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设
nums[-1] = nums[n] = -∞。你必须实现时间复杂度为
O(log n)的算法来解决此问题。示例 1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。示例 2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2; 或者返回索引 5, 其峰值元素为 6。提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
题目解析:
这道题目类似于我们之前做过的山脉数组的峰顶索引那道题目。就是给你一个山峰数组 nums,让我们返回对应山峰元素的索引,但是不同于那一道题目,这一道题目的 nums 中会有多个山峰值,只要返回其中一个就可以了。比如 nums = [1, 2, 1, 3, 4, 6, 8],返回值就是 1 或者 6,因为 nums[1] = 2,会大于两边的1;nums[6] = 8,会大于左边的6,但是由于是最后一个,而后面的高度值是被假设为了负无穷,所以 8 也是一个山峰值。
算法解析:
我们可以先想一个暴力解法。暴力解法很简单,就是从头遍历数组,如果 nums[i] > nums[i + 1],那就返回 i;边界情况就是 i == nums.size() - 1 时,此时如果还没有返回,继续判断 nums[i + 1] 会越界,而且说明 nums.size() - 1 位置就是峰顶,所以返回 nums.size() - 1 即可:
cpp
class Solution {
public:
int findPeakElement(vector<int>& nums)
{
for (int i = 0; i < nums.size() - 1; i++)
{
if (nums[i] > nums[i + 1]) return i;
}
//到这,说明前 n - 1 个元素都不是山峰
return nums.size() - 1;
}
};显然,这个时间复杂度是 O(n) 的。
那么我们可不可以优化一下呢?我们可以发现如果以山峰元素为界,那么可以分为两部分,左边是 nums[i] < nums[i + 1],右边为 nums[i] > nums[i + 1],所以我们发现 nums 具有二段性,我们就可以采用二分查找算法了。我们开始让 left = 0, right = nums.size() - 1,如果 nums[mid]< nums[mid + 1],那么此时的 mid 及左边的元素绝对不可能是山峰值,所以我们直接让 left = mid + 1,如果 nums[mid] > nums[mid + 1],此时 mid 是可能成为山峰元素的,所以我们需要让 right = mid,这样查找到最后,当 right = left 时,nums[left] 就是山峰值。
在这里结合模板,给大家说一个编写二分查找代码的小技巧,二分查找的中点与循环条件是重点。对于查找左边界与右边界的二分,循环条件都是 left < right,主要就是求中点的方式不一样。如果我们在分析过程中,发现 left = mid + 1 的,此时下面有 + 1,那么上面的求中点就没有 + 1,也就是 mid = left + (right - left) / 2;如果是 left = mid 没有 + 1,那么上面的中点就是 mid = left + (right - left + 1) / 2,此时中点需要 + 1。
代码:
cpp
class Solution {
public:
int findPeakElement(vector<int>& nums)
{
int left = 0, right = nums.size() - 1;
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1]) right = mid;
else left = mid + 1;
}
return left;
}
};因为在代码中出现了 left = mid + 1,所以上面的 mid = left + (right - left) / 2,就没有 + 1,这样就可以只分析两边的情况就可以了,模板就比较好记了。显然,时间复杂度是 O(logn) 的。