1 随机构造法
Robert Gallager 提出LDPC 码的同时提出了随机构造LDPC 码的算法，主要构造方法如下所示：
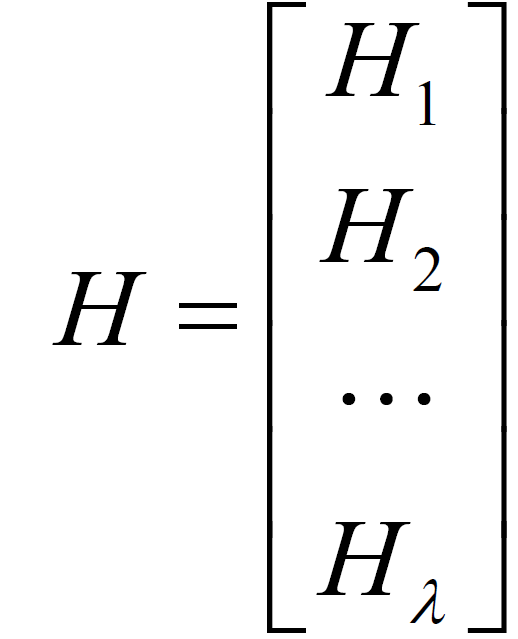
式中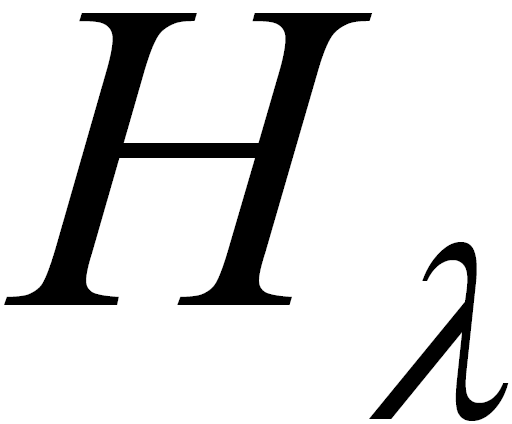
是
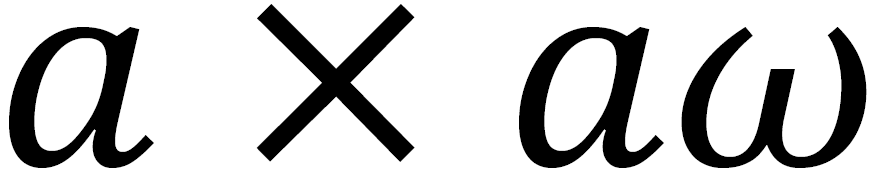的矩阵，是校验矩阵的子矩阵，子矩阵中满足构造的要求，每个子矩阵的行重都为ω，列重都为1，这样就会避免有两行或者两列同一位置元素同时为1，α 和ω 的值均是大于1 的，
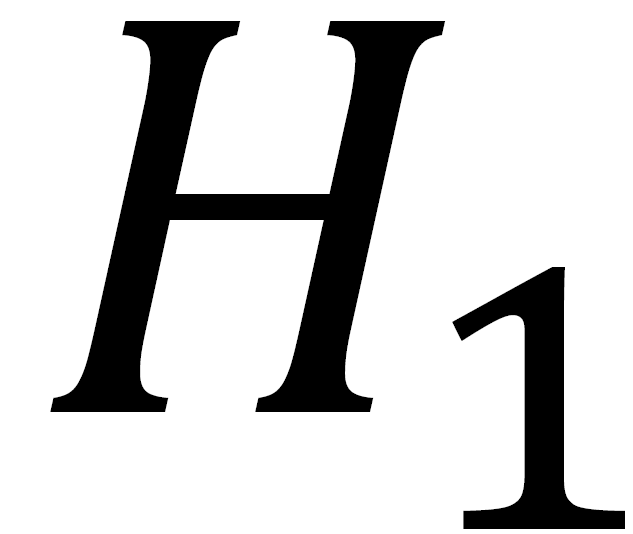矩阵构造完成后，其他的子矩阵由矩阵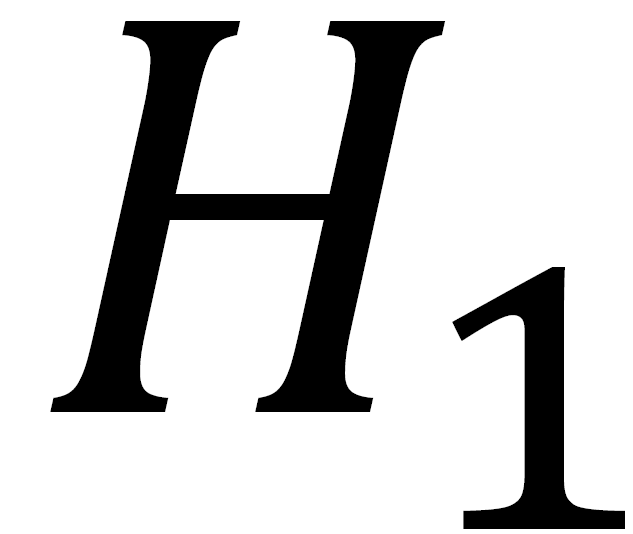的列互相交换，组合排列构成LDPC码的校验矩阵虽然这种方法构造出来的LDPC码符合约束条件，但LDPC码性能的影响因素之一最小围长没有办法保证在一个较大的水平。
这种列的随机置换也会带来girth-4 和girth-6。为了减少这种短环对性能的影响就要借助计算机在构造过程中对短环进行检查和对这些环所在的行或者列进行随机化的调整，这种过程一定会大大增加编码构造的复杂度，而且有些情况短环仅仅依靠计算机可能无法消除，码的性能不能得到绝对的保证。
2 PEG 构造法
Xiaoyu Hu 等人提出了一种渐进边增长的算法，它是一种贪心算法，在需要校验矩阵的围长较大时，PEG算法的优势明显，PEG 算法是按照逐条边添加的方法构造Tanner图的，在每一条边添加时，尽量保证局部围长最大。
PEG算法构造LDPC码的前提条件是已知码长和码率，从码长和码率就可以得知校验节点和变量节点的个数，还需要给出节点的度分布。
采用PEG 算法构造LDPC 码需要遵循一个准则：添加新的边时要尽量减少对当前图的围长的影响，使围长最大化。
在构造规则LDPC 码和非规则LDPC 码时，PEG 算法都是一种非常良好的构造方法，构造出的LDPC 码具有非常良好的性能。
考虑一个Tanner 图（V，E），V 表示的是节点的集合，且有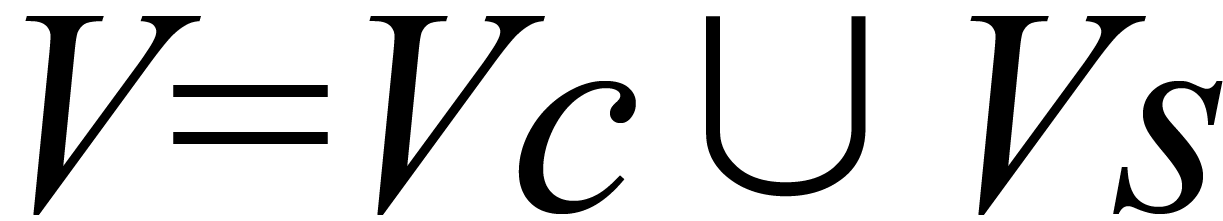
,其中，校验节点集合
、变量节点集合
、边的集合E 之前的关系为
。
如果第i个变量节点与第j个校验节点相连接，有
。
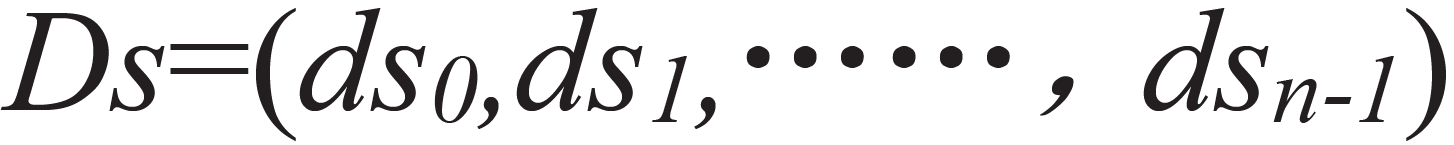表示的是已经设计好的变量节点的度分布。
节点
的度分布表示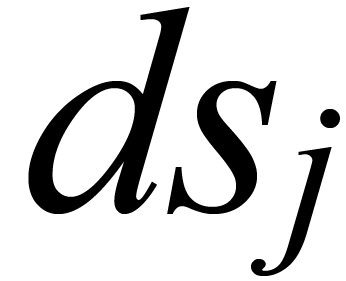
。且度分布
已经按照非递减的原则排列好。
是与变量节点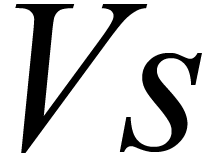
相连的所有边的集合，其中，
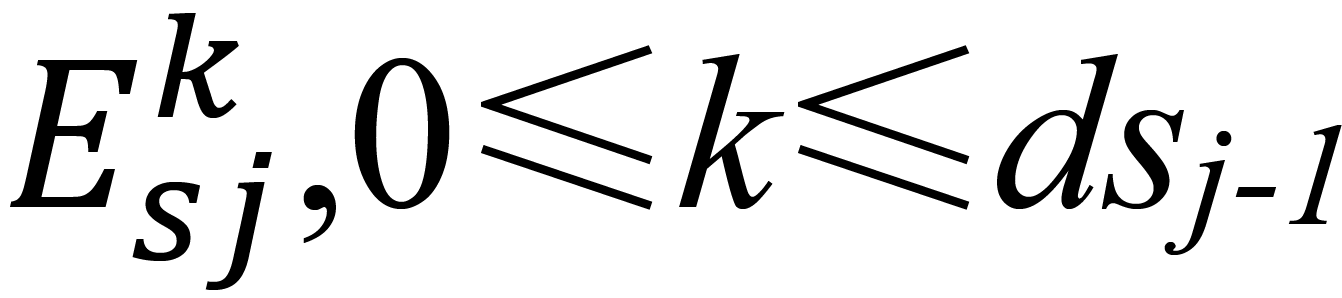是与变量节点相连的第k条边。
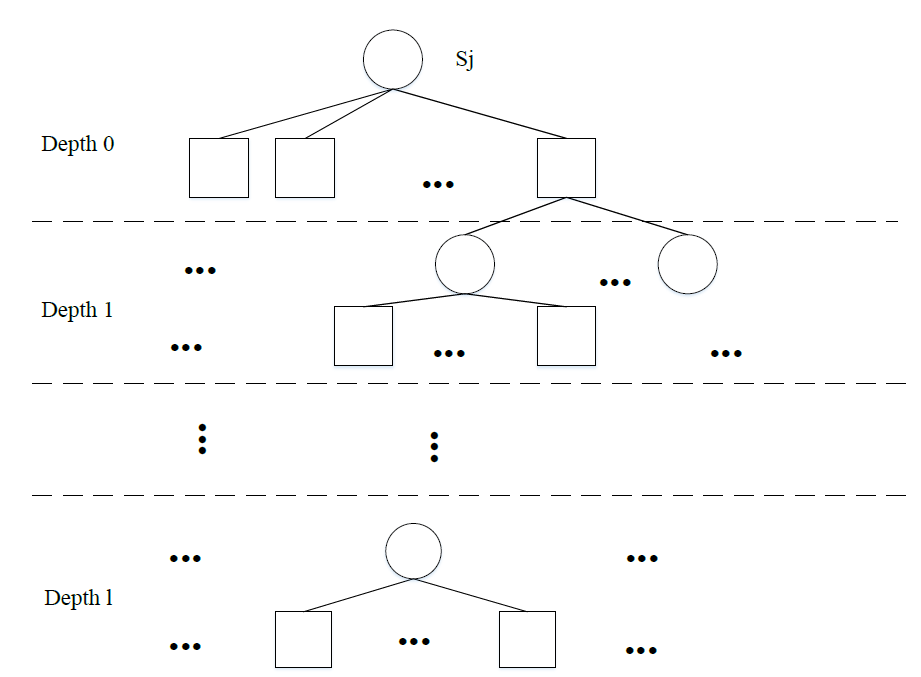
下图所示是一个LDPC 码校验矩阵以变量节点展开成一个深度为l的树，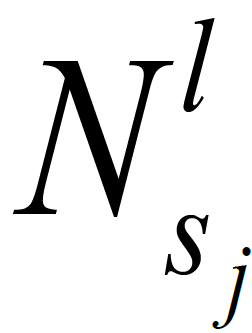
是变量节点........深度为l的邻居的校验节点集合，
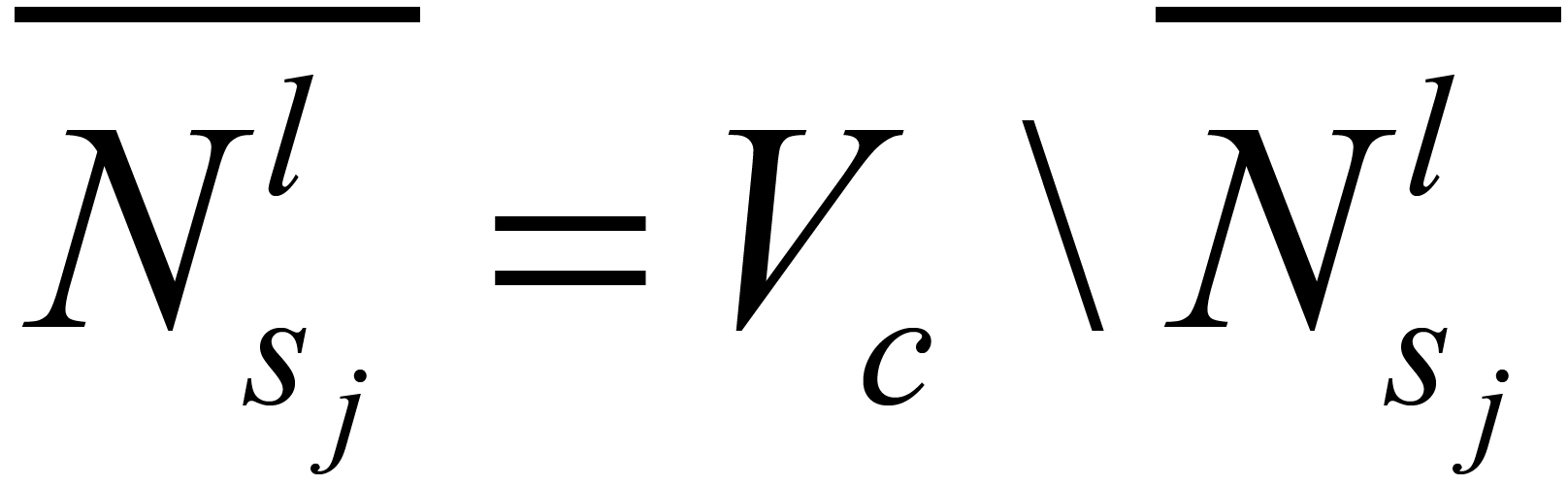是它的补集，也就是说
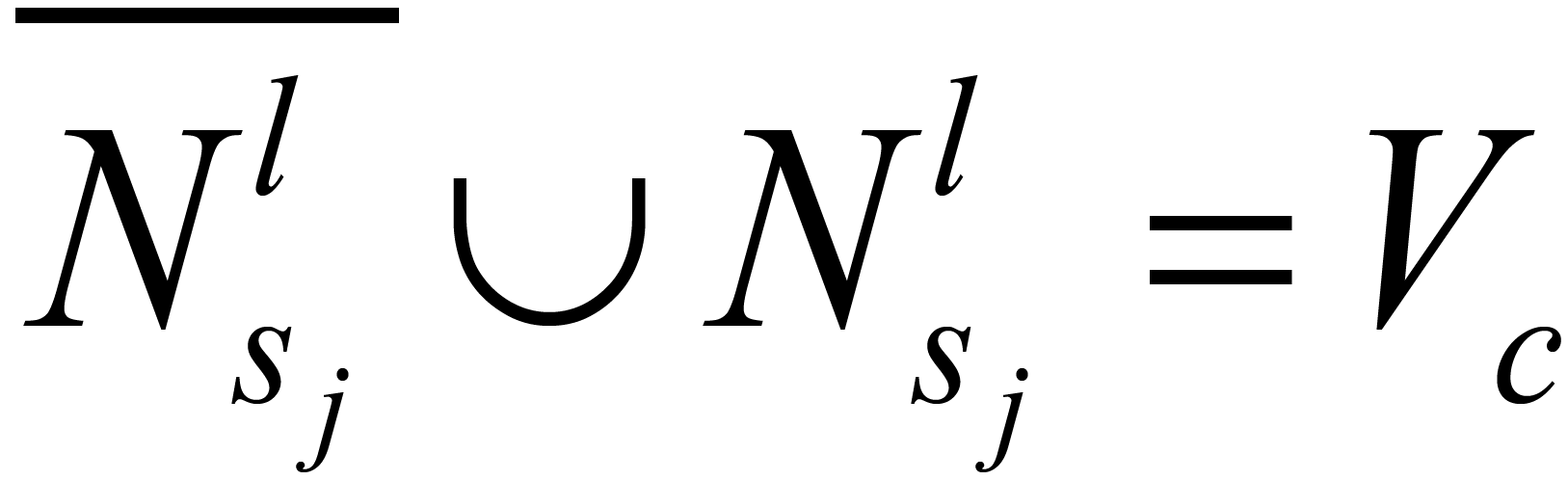。详细的 PEG算法流程如下表所示。
3 准循环构造法
准循环构造方法也是由Gallager 博士提出的一种LDPC 码的构造算法，这种准循环构造方法的思想是将一个大的校验矩阵H分成多个子矩阵，所以在进行构造时，要首先确定好子矩阵的大小，如下式描述这种关系。
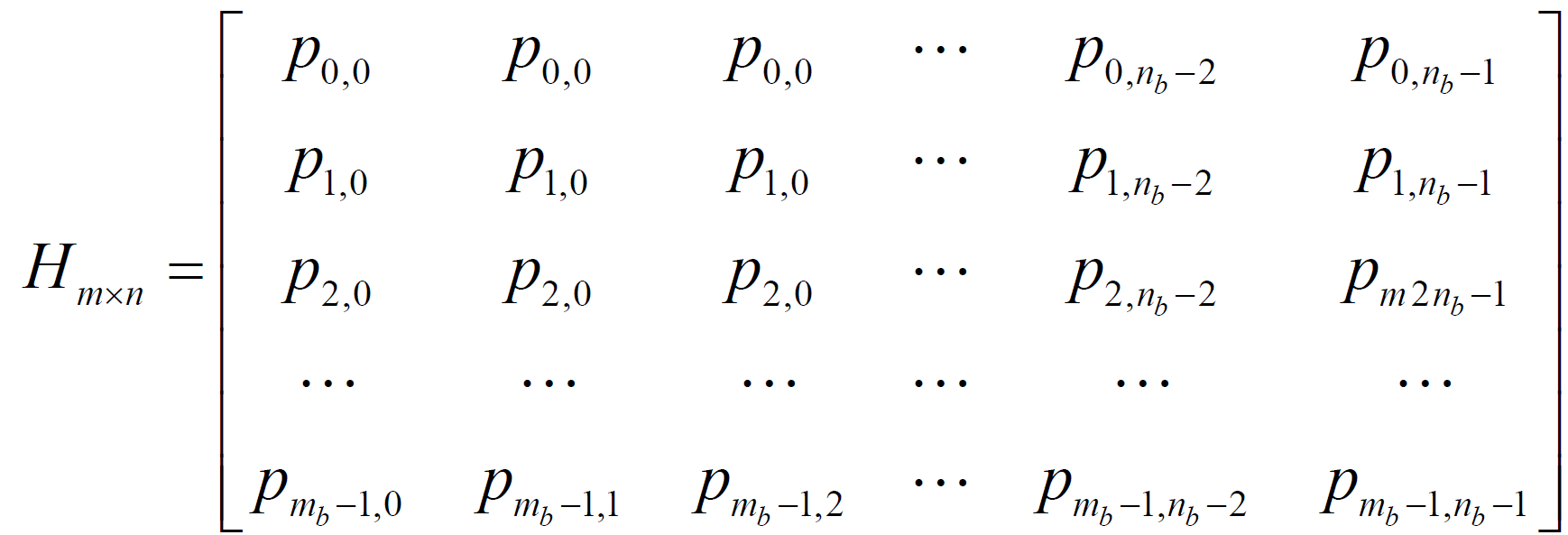
式子表示一个m行n列的校验矩阵，式子中以基校验矩阵形式表示，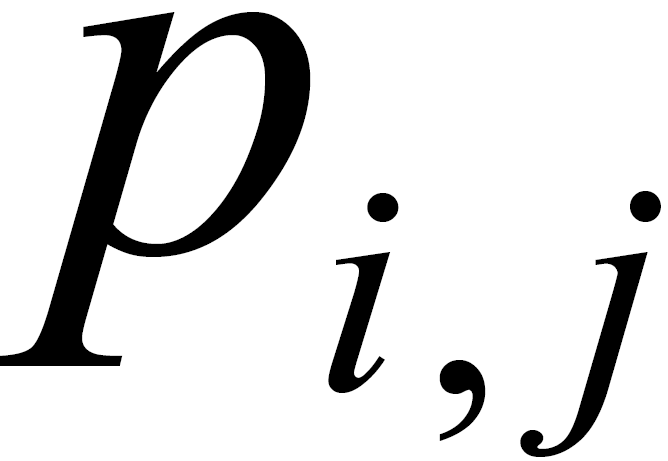
是大小为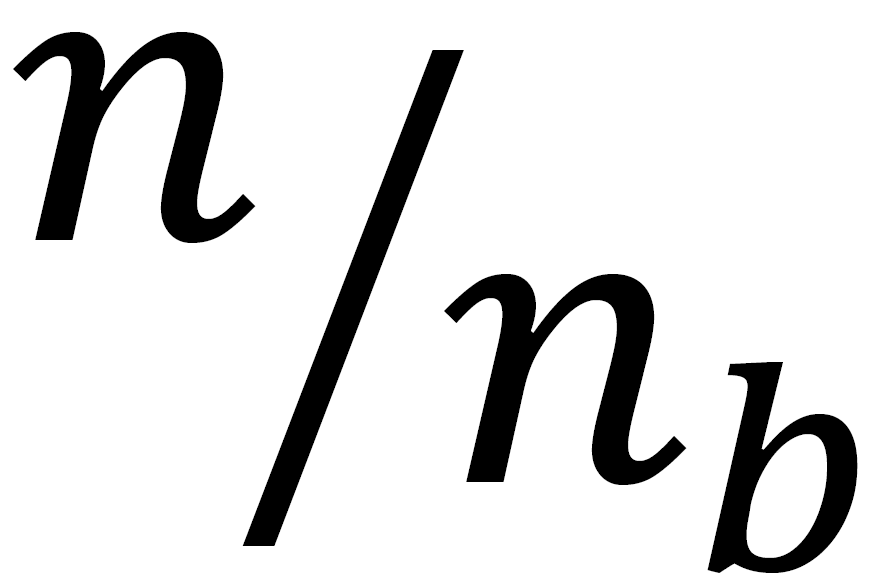
的子矩阵，一般的表示方法中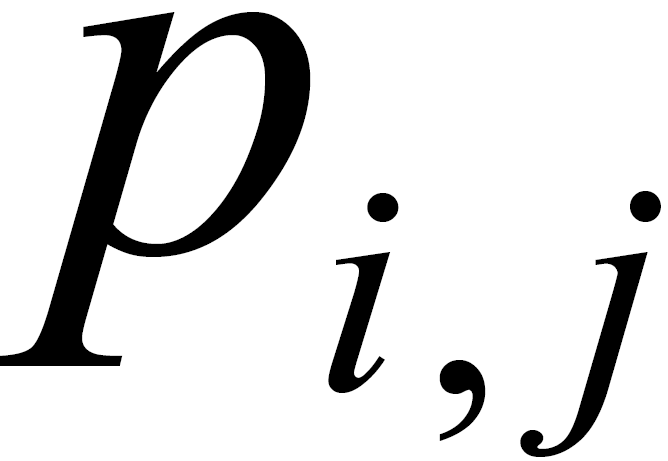，的值如果为负数，那么经过扩展得的这个子矩阵就是全零矩阵；如果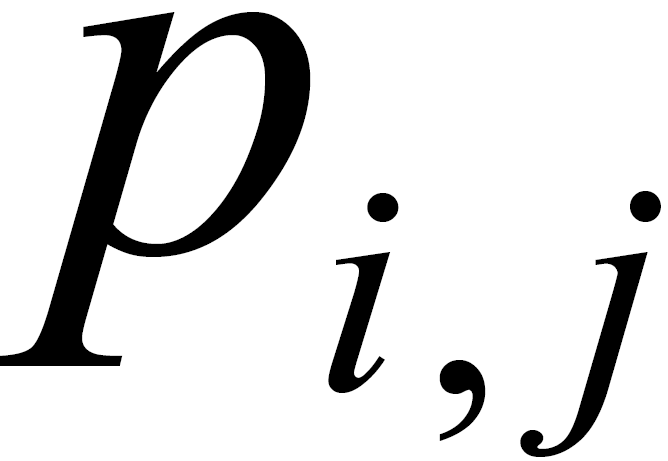的值为0，也就是单位矩阵循环移位0次，即就是单位阵；若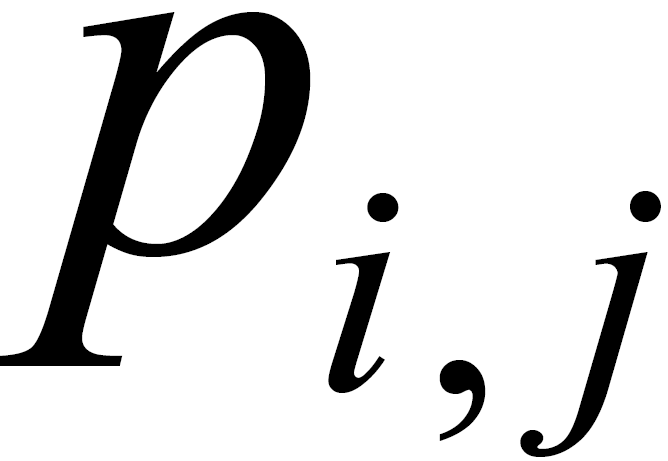为具体的正数，就表示该子矩阵是单位矩阵循环移位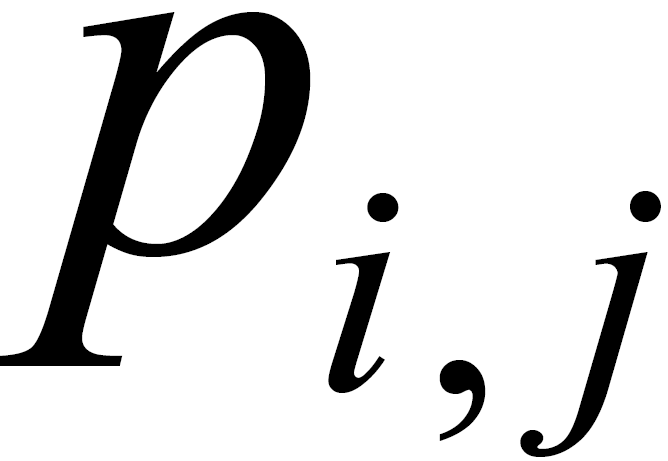次。
可以看出循环矩阵的构造过程需要一个从基矩阵扩展到校验矩阵的过程，所谓扩展就将各个子矩阵进行逐行逐列的拼接。用这样的方法构造出来的校验矩阵非常容易构造出行重为n，列重为m的矩阵，而且避免了出现围长为4 的短环的情况，避免了变量节点到校验节点连线过于集中的问题，大大改善了译码性能。
使用这种结构化的矩阵构造出来的LDPC 码就是准循环LDPC 码，即QC-LPDC 码，这种码字结构，在编译码方面的复杂度较低，在硬件实现上更为容易。