一、差分算法简介
1.1 简介
差分算法的核心在于构建差分数组或矩阵 ,将对原始数据的复杂区间操作转化为对差分数组特定端点值的简单操作 ,从而实现对原数组的高效区间修改。在面对频繁对数组某个区间的元素进行增减操作时,传统方法往往需要对区间内每个元素逐一处理,时间复杂度较高;而差分算法通过巧妙的转换,将这类操作的时间复杂度降至 O (1),大大提升了处理效率。
差分适用于频繁对原始数组的某个区间的元素进行增减
二、差分算法基础理论
2.1 一维差分
2.1.1 差分数组的概念
对于一个给定的一维数组 arr(长度为 length),其差分数组 diff 定义如下:diff[0] = arr[0],对于 i > 0,diff[i] = arr[i] - arr[i - 1]。差分数组记录了原始数组中相邻元素之间的差异。例如,原始数组 arr = [1, 3, 5, 7, 9],其差分数组 diff = [1, 2, 2, 2, 2]。
2.1.2 性质与原理
差分数组的核心性质:差分数组的前缀和即为原始数组。即对于任意的 i,有 arr[i] = diff[0] + diff[1] + ... + diff[i]。
当需要对原始数组的区间 [l, r](0-based)进行 +k 操作时,仅需修改差分数组的两个端点:diff[l] += k、diff[r + 1] -= k。
避免边界判断的关键:一维场景中,若 r + 1 超出原始数组长度(即 r = length - 1),diff[r + 1] 的修改会作用于数组外的 "虚拟位置",但由于后续计算前缀和时仅遍历到 length - 1,该修改不会影响结果,因此无需额外判断 r + 1 < length。
2.1.3 做题步骤与代码实现
以 "区间加法" 问题为例:给定初始长度为 length 的全 0 数组,和一系列更新操作 updates(updates[i] = [startIdx, endIdx, inc]),返回执行完所有操作后的数组。
核心操作
java
diff[left] += val;
diff[right + 1] -= val;定义差分数组:直接初始化长度为 length + 1 的差分数组(额外的 1 个位置用于容纳 r + 1 超出边界的情况),无需判断边界
差分数组前缀和即为结果数组
java
int[] result = new int[length];
result[0] = diff[0];
for (int i = 1; i < length; i++) {
result[i] = result[i - 1] + diff[i];
}模板代码演示
java
public int[] getModifiedArray(int length, int[][] updates) {
// 差分数组长度设为 length + 1,避免边界判断
int[] diff = new int[length + 1];
// 步骤 2:处理所有区间更新(无需判断 endIdx + 1 是否越界)
for (int[] update : updates) {
int start = update[0];
int end = update[1];
int val = update[2];
diff[start] += val;
diff[end + 1] -= val; // 即使 end+1 = length,也不会越界
}
// 步骤 3:计算前缀和,还原结果数组
int[] result = new int[length];
result[0] = diff[0];
for (int i = 1; i < length; i++) {
result[i] = result[i - 1] + diff[i];
}
return result;
}2.2 二维差分
2.2.1 核心操作及逻辑
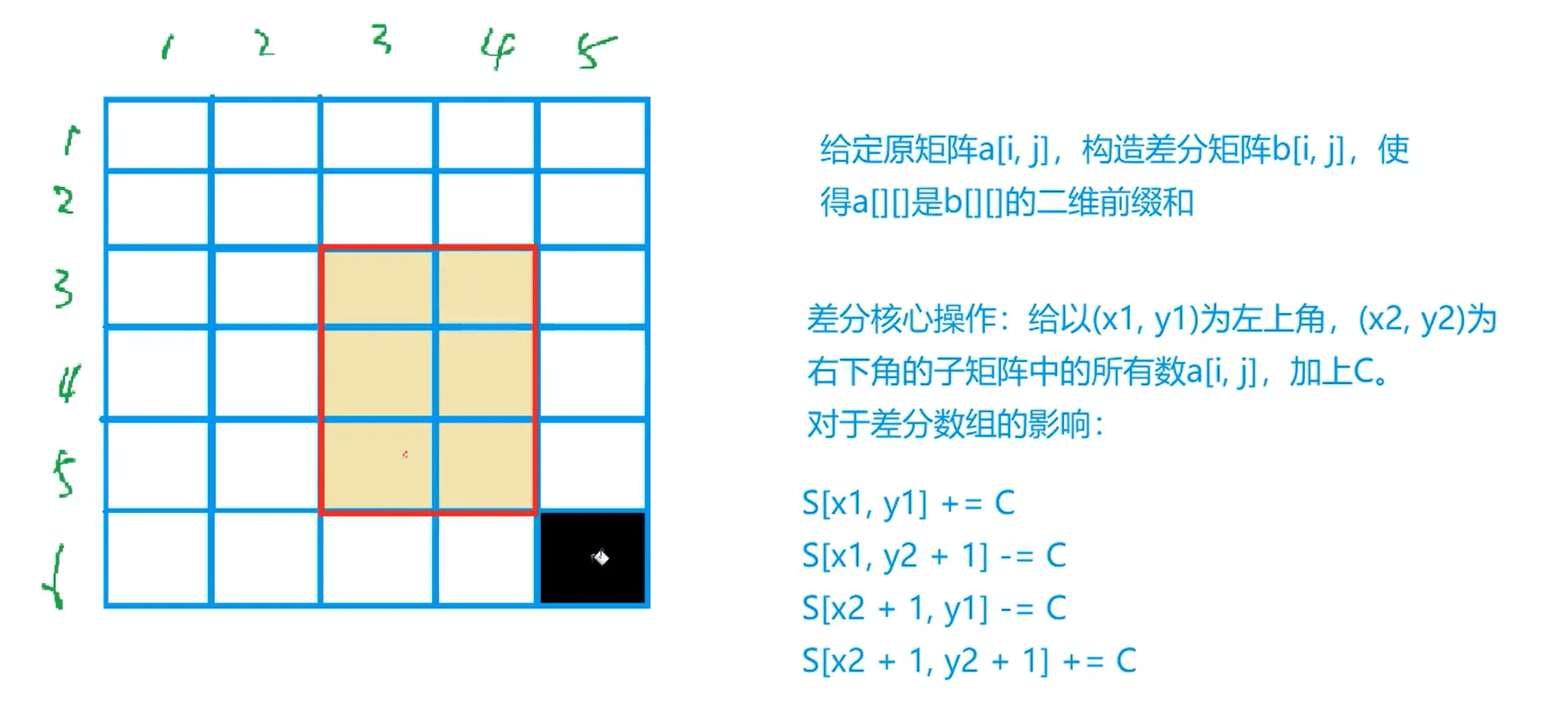
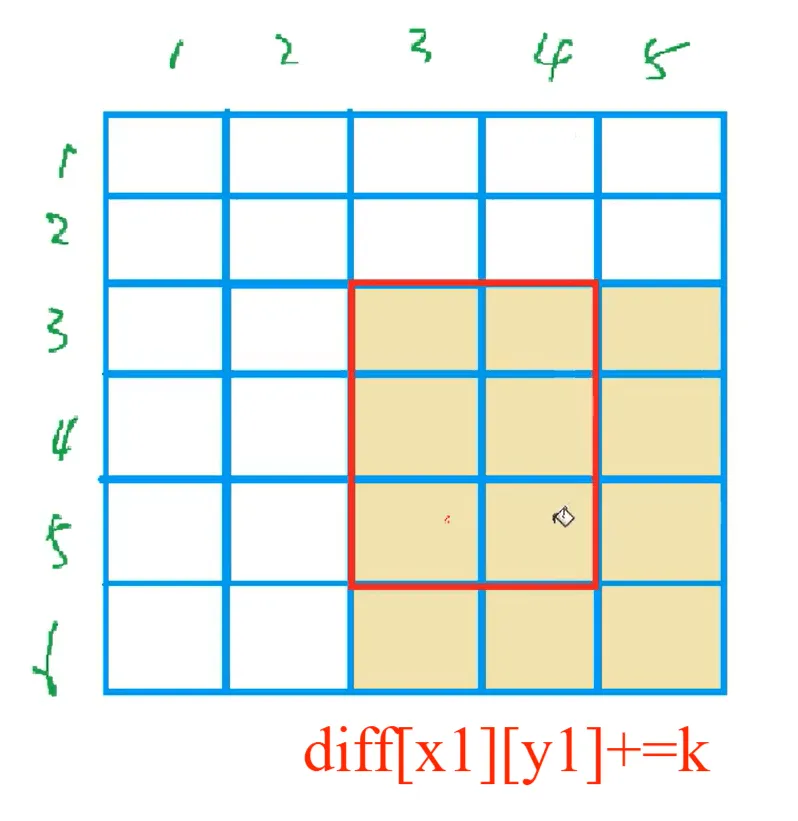
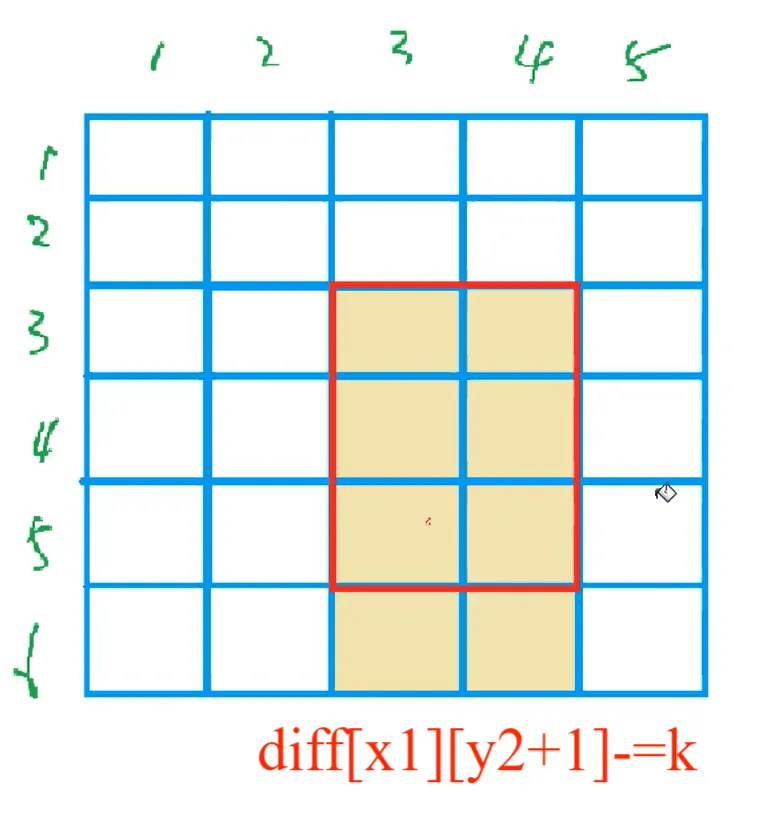
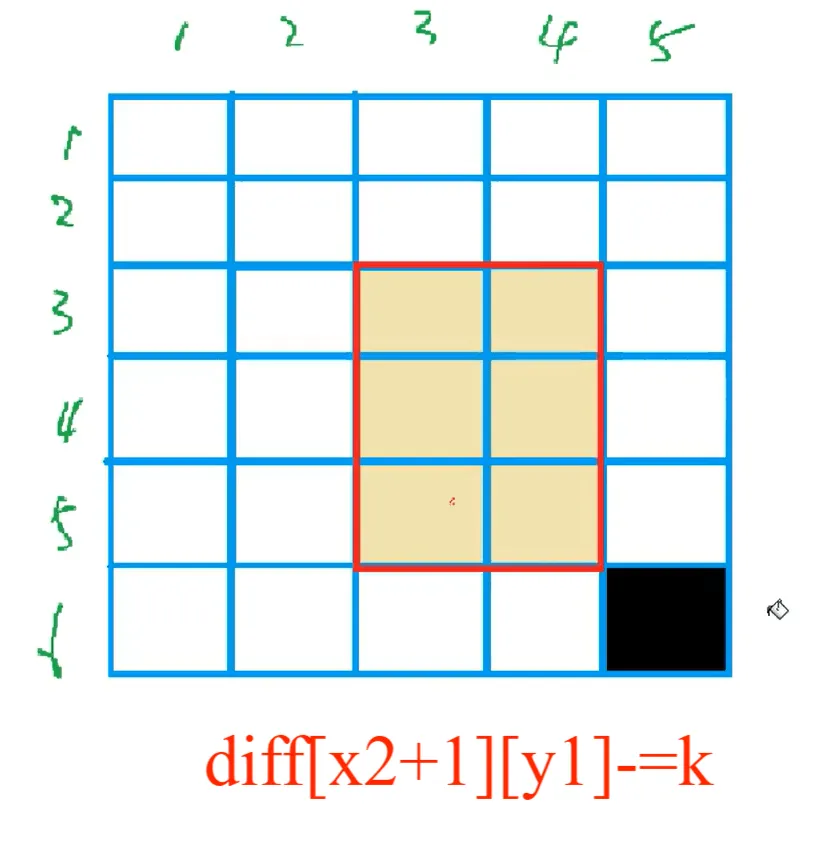
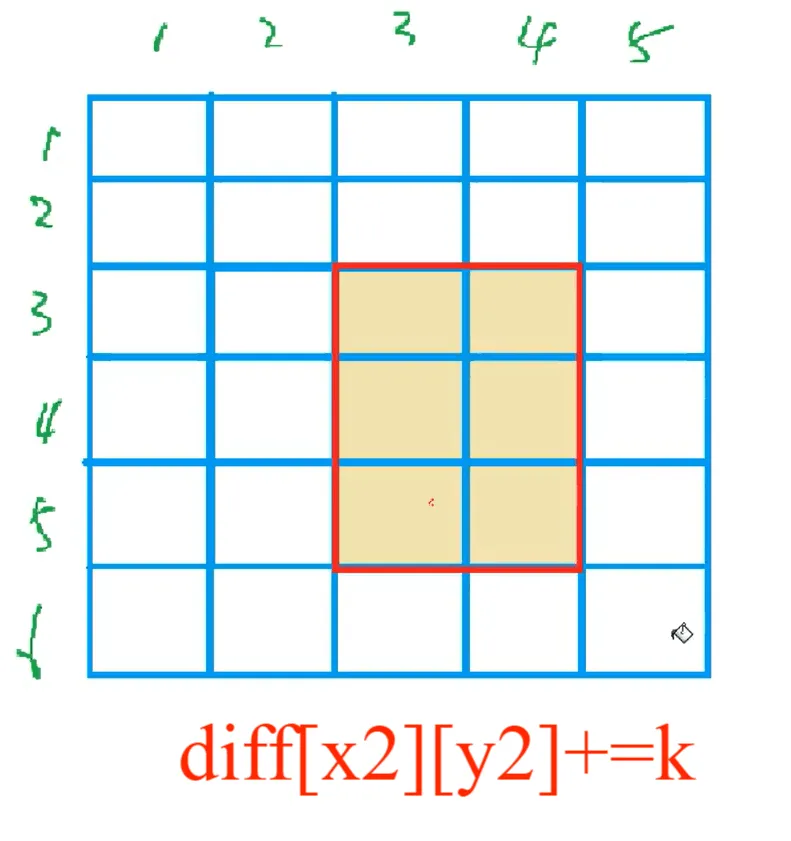
避免边界判断的关键:将差分矩阵的尺寸设为 (m + 2) × (n + 2)(比原始矩阵多 1 行 1 列),即使 x2 + 1 = m + 1 或 y2 + 1 = n + 1,修改也不会越界,且后续计算前缀和时仅遍历原始矩阵的 m × n 范围,多余位置的修改不影响结果。
2.2.2 初始化差分矩阵
二维差分的初始化本质是:将原始矩阵的每个元素 matrix[i][j](1-based)视为 1×1 的矩形区域,执行 +matrix[i][j] 操作。利用 (m + 2) × (n + 2) 的差分矩阵,无需判断 i+1 或 j+1 是否越界。
初始化代码实现
java
// 初始化: 对 (i,j)~(i,j) 执行 +val 操作
diff[i][j] += val;
diff[i][j + 1] -= val;
diff[i + 1][j] -= val;
diff[i + 1][j + 1] += val;2.2.3 子矩阵更新与恢复原矩阵
子矩阵更新:这是最核心的步骤
java
// 对矩形区域 (x1,y1)~(x2,y2) 执行 +val 操作
public void updateDiffMatrix(int[][] diff, int x1, int y1, int x2, int y2, int val) {
diff[x1][y1] += val;
diff[x1][y2 + 1] -= val;
diff[x2 + 1][y1] -= val;
diff[x2 + 1][y2 + 1] += val; // 无需判断 x2+1、y2+1 是否越界
}恢复原矩阵:二维前缀和即为结果数组
java
// 根据差分矩阵恢复 m 行 n 列的原始矩阵(1-based)
public int[][] recoverOriginalMatrix(int[][] diff, int m, int n) {
int[][] matrix = new int[m + 1][n + 1]; // 1-based 存储结果
// 计算二维前缀和(先按行,再按列)
for (int i = 1; i <= m; i++) {
int rowSum = 0;
for (int j = 1; j <= n; j++) {
rowSum += diff[i][j];
matrix[i][j] = matrix[i - 1][j] + rowSum;
}
}
return matrix;
}三、差分算法适用场景
3.1 一维差分适用场景
批量数据区间调整
例如电商平台的 "限时折扣":某商品的每日价格存储在数组中,需对 [活动开始日, 活动结束日] 的价格统一减去折扣金额。使用一维差分(差分数组长度设为 n + 1),无需判断边界,直接修改区间端点即可。
统计区间覆盖次数
例如地铁客流量统计:给定每个乘客的乘车时间段 [进站时间, 出站时间],统计每个时间点的在站人数。通过差分将 "时间段覆盖" 转化为 diff[进站] += 1、diff[出站 + 1] -= 1,无需判断边界,最终前缀和即为每个时间点的人数。
3.2 二维差分适用场景
图像处理中的矩形区域调整
例如图像亮度增强:对 800×600 图像的 (100,200)~(300,400) 区域亮度 +50。使用 (802×602) 的差分矩阵,直接执行 4 个端点的修改,无需判断 300+1 或 400+1 是否越界,效率显著高于逐像素遍历。
网格地图的区域状态更新
例如游戏地图的 "技能效果":在 100×100 的网格中,技能对 (x1,y1)~(x2,y2) 区域的敌人造成伤害。通过 (102×102) 的差分矩阵记录伤害值,后续计算前缀和即可得到每个敌人的总伤害,避免边界判断逻辑。
四、差分算法初始化情况分析
4.1 何时无需初始化?
当原始数组 / 矩阵的初始值为 全 0 时,差分数组 / 矩阵默认初始化为全 0 即可,无需额外操作。例如 "区间加法" 问题中初始数组为全 0,直接使用 new int[length + 1] 初始化差分数组,无需基于原始数组计算初始差分。
4.2 何时需要初始化?
当原始数组 / 矩阵存在 非 0 初始值 时,需将初始状态转化为差分更新操作(即 "初始化差分")。例如原始数组 arr = [3,5,4,6] 或原始矩阵 matrix = [[1,2],[3,4]],需通过遍历原始数据,对每个元素执行 "单点更新" 操作,构建初始差分数组 / 矩阵。
4.3 二维差分初始化示例(避免边界判断)
以 3×3 原始矩阵(1-based)matrix = [[0,0,0,0],[0,1,2,3],[0,4,5,6],[0,7,8,9]](第 0 行第 0 列为占位符)为例,初始化差分矩阵的过程:
- 差分矩阵尺寸设为 (3+2) × (3+2) = 5×5,初始全 0。
- 对 matrix[1][1] = 1 执行单点更新:diff[1][1] +=1、diff[1][2]-=1、diff[2][1]-=1、diff[2][2]+=1。
- 对 matrix[1][2] = 2 执行单点更新:diff[1][2] +=2、diff[1][3]-=2、diff[2][2]-=2、diff[2][3]+=2。
- 依次遍历所有元素,最终得到初始差分矩阵。
核心优势:整个过程无需判断 i+1 或 j+1 是否超出原始矩阵范围(如 i=3 时 i+1=4,仍在 5×5 差分矩阵内),代码简洁且无越界风险。
五、经典例题
5.1 一维差分

java
class Solution {
public int[] corpFlightBookings(int[][] bookings, int n) {
int[] diff = new int[n];
for (int[] booking : bookings) {
int first = booking[0] - 1;
int last = booking[1] - 1;
int seats = booking[2];
// 区间更新
diff[first] += seats;
if (last < diff.length - 1) {
diff[last + 1] -= seats;
}
}
int[] ans = new int[diff.length];
ans[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
ans[i] = ans[i - 1] + diff[i];
}
return ans;
}
}
java
class Solution {
public boolean carPooling(int[][] trips, int capacity) {
int[] diff = new int[1001];
for (int[] trip : trips) {
int num = trip[0];
int from = trip[1];
int to = trip[2];
diff[from] += num;
diff[to] -= num;
}
int res = diff[0];
if (res > capacity)
return false;
for (int i = 1; i < diff.length; i++) {
res = res + diff[i];
if (res > capacity) {
return false;
}
}
return true;
}
}5.2 二维差分 

java
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int q = sc.nextInt();
// 消耗换行符
sc.nextLine();
int[][] matrix = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
String line = sc.nextLine();
for (int j = 1; j <= m; j++) {
char c = line.charAt(j - 1);
if (c == 'B') {
matrix[i][j] = 1;
}
}
}
//n + 2 避免边界判断
int [][] diff = new int[n + 2][m + 2];
for(int T = 0;T < q; T++) {
int x1 = sc.nextInt();
int y1 = sc.nextInt();
int x2 = sc.nextInt();
int y2 = sc.nextInt();
//二维差分核心操作
diff[x1][y1] += 1;
diff[x1][y2 + 1] -=1;
diff[x2 + 1][y1] -=1;
diff[x2 + 1][y2 + 1] += 1;
}
int[][] pre = new int[n + 1][m + 1];
int ans = 0;
//差分数组前缀和即为结果数组
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
pre[i][j] = pre[i - 1][j] + pre[i][j - 1]
- pre[i - 1][j - 1] + diff[i][j];
if(pre[i][j] >= 1 || matrix[i][j] == 1) {
ans++;
}
}
}
System.out.println(ans);
}
}