从零开始的C++学习生活 20:数据结构与STL复习课(4.4w字全解析)

Yupureki2025-11-02 17:20

个人主页:Yupureki-CSDN博客

C++专栏:C++_Yupureki的博客-CSDN博客

目录

前言

[1. 复杂度计算](#1. 复杂度计算)

[1.1 什么是算法复杂度？](#1.1 什么是算法复杂度？)

[1.2 复杂度的类型](#1.2 复杂度的类型)

[1. 时间复杂度](#1. 时间复杂度)

[2. 空间复杂度](#2. 空间复杂度)

[1.3 常见的时间复杂度](#1.3 常见的时间复杂度)

[1.3.1 常数时间复杂度](#1.3.1 常数时间复杂度)

[1.3.2 对数时间复杂度](#1.3.2 对数时间复杂度)

[1.3.3 线性时间复杂度](#1.3.3 线性时间复杂度)

[1.3.4 线性对数时间复杂度](#1.3.4 线性对数时间复杂度)

[1.3.5 平方时间复杂度](#1.3.5 平方时间复杂度)

[1.4 常见的空间复杂度](#1.4 常见的空间复杂度)

[1.4.1 O(1)空间复杂度](#1.4.1 O(1)空间复杂度)

[1.4.2 O(N)空间复杂度](#1.4.2 O(N)空间复杂度)

[1.4.3 O(N^2)空间复杂度](#1.4.3 O(N^2)空间复杂度)

[1.5 复杂度的主要作用](#1.5 复杂度的主要作用)

[2. 线性数据结构](#2. 线性数据结构)

[2.1 顺序表](#2.1 顺序表)

增

删

查

[2.2 链表](#2.2 链表)

增

删

查

[2.3 栈](#2.3 栈)

压栈

出栈

获取栈顶元素

[2.4 队列](#2.4 队列)

入队

出队

获取队头数据

[3. 非线性数据结构](#3. 非线性数据结构)

[3.1 树](#3.1 树)

[3.1.1 树的概念](#3.1.1 树的概念)

[3.1.2 树的常见术语和表示](#3.1.2 树的常见术语和表示)

常见术语

树的表示

[3.2 二叉树](#3.2 二叉树)

[3.2.1 二叉树的种类](#3.2.1 二叉树的种类)

满二叉树

完全二叉树

[3.2.2 堆](#3.2.2 堆)

[3.2.2.1 堆的概念](#3.2.2.1 堆的概念)

[3.2.2.2 数组实现堆的基础结构](#3.2.2.2 数组实现堆的基础结构)

[3.2.2.3 堆的创建与销毁](#3.2.2.3 堆的创建与销毁)

[3.2.2.4 向上调整算法](#3.2.2.4 向上调整算法)

[3.2.2.5 向下调整算法](#3.2.2.5 向下调整算法)

[3.2.2.6 堆排序](#3.2.2.6 堆排序)

[3.2.2.7 TOP-K问题](#3.2.2.7 TOP-K问题)

[3.3 二叉搜索树](#3.3 二叉搜索树)

[3.3.1 二叉搜索树的概念](#3.3.1 二叉搜索树的概念)

[3.3.2 二叉搜索树的性能分析](#3.3.2 二叉搜索树的性能分析)

[3.3.3 构建基础二叉搜索树](#3.3.3 构建基础二叉搜索树)

[3.3.3.1 查找](#3.3.3.1 查找)

[3.3.3.2 插入](#3.3.3.2 插入)

[3.3.3.3 删除](#3.3.3.3 删除)

[3.3.4 二叉搜索树的局限性](#3.3.4 二叉搜索树的局限性)

[3.3.4.1 时间复杂度分析](#3.3.4.1 时间复杂度分析)

[3.3.4.2 局限性](#3.3.4.2 局限性)

[3.4 AVL树](#3.4 AVL树)

[3.4.1 AVL树的概念](#3.4.1 AVL树的概念)

[3.4.2 AVL树的构建](#3.4.2 AVL树的构建)

[3.4.2.1 插入](#3.4.2.1 插入)

[3.4.2.2 旋转](#3.4.2.2 旋转)

左单旋

右单旋

左右双旋

右左双旋

[3.5 红黑树](#3.5 红黑树)

[3.5.1 红黑树的概念](#3.5.1 红黑树的概念)

[3.5.2 红黑树的规则](#3.5.2 红黑树的规则)

[3.5.3 红黑树的构建](#3.5.3 红黑树的构建)

[3.5.3.1 插入](#3.5.3.1 插入)

[3.5.3.2 变色](#3.5.3.2 变色)

叔叔节点存在且为红色 (变色)

叔叔节点不存在或为黑色（旋转+变色）

[3.6 AVL树和红黑树的区别](#3.6 AVL树和红黑树的区别)

[3.6.1 基本性质差异](#3.6.1 基本性质差异)

AVL树

红黑树

[3.6.2 效率对比](#3.6.2 效率对比)

[3.6.2.1 时间复杂度](#3.6.2.1 时间复杂度)

[3.6.2.2 实际性能差异](#3.6.2.2 实际性能差异)

[3.6.3 核心区别对比](#3.6.3 核心区别对比)

[3.6.4 实际应用中的选择](#3.6.4 实际应用中的选择)

[3.7 哈希](#3.7 哈希)

[3.7.1 哈希概念](#3.7.1 哈希概念)

[3.7.2 哈希冲突](#3.7.2 哈希冲突)

[3.7.3 哈希函数](#3.7.3 哈希函数)

[3.7.3.1 除法散列法/除留余数法](#3.7.3.1 除法散列法/除留余数法)

[3.7.3.2 乘法散列法](#3.7.3.2 乘法散列法)

[3.7.4 处理哈希冲突](#3.7.4 处理哈希冲突)

[3.7.4.1 开放定址法](#3.7.4.1 开放定址法)

线性探测

二次探测

开放定址法代码实现

[3.7.4.2 链地址法(哈希桶)](#3.7.4.2 链地址法(哈希桶))

链地址法代码实现

极端情况下的哈希桶改良

[3.7.5 效率分析](#3.7.5 效率分析)

[3.7.5.1 时间复杂度分析](#3.7.5.1 时间复杂度分析)

[3.7.5.2 空间复杂度分析](#3.7.5.2 空间复杂度分析)

[3.8 位图](#3.8 位图)

[3.8.1 位图的概念](#3.8.1 位图的概念)

[3.8.2 位图的实现](#3.8.2 位图的实现)

[3.8.3 位图的实际用处](#3.8.3 位图的实际用处)

[3.9 布隆过滤器](#3.9 布隆过滤器)

[3.9.1 布隆过滤器的概念](#3.9.1 布隆过滤器的概念)

[3.9.2 布隆过滤器原理](#3.9.2 布隆过滤器原理)

[3.9.3 基础实现](#3.9.3 基础实现)

[4. 排序算法](#4. 排序算法)

[4.1 插入排序](#4.1 插入排序)

直接插入排序

希尔排序

[4.2 选择排序](#4.2 选择排序)

直接选择排序

堆排序

[4.3 交换排序](#4.3 交换排序)

冒泡排序

快速排序

非递归快速排序

[4.4 归并排序](#4.4 归并排序)

递归版

非递归版

[4.5 计数排序](#4.5 计数排序)

[4.6 性能对比](#4.6 性能对比)

如何选择合适的排序算法

[5. STL常见的容器](#5. STL常见的容器)

[5.1 序列式容器](#5.1 序列式容器)

[5.1.1 string](#5.1.1 string)

[5.1.1.1 构建string](#5.1.1.1 构建string)

[5.1.1.2 容量操作](#5.1.1.2 容量操作)

[5.1.1.3 string的修改操作](#5.1.1.3 string的修改操作)

[5.1.1.4 访问和遍历](#5.1.1.4 访问和遍历)

[5.1.2 vector](#5.1.2 vector)

[5.1.2.1 构造vector](#5.1.2.1 构造vector)

[5.1.2.2 容量管理](#5.1.2.2 容量管理)

[5.1.2.3 元素访问](#5.1.2.3 元素访问)

[5.1.2.4 修改操作](#5.1.2.4 修改操作)

[5.1.3 list](#5.1.3 list)

[5.1.3.1 构造list](#5.1.3.1 构造list)

[5.1.3.2 迭代器使用](#5.1.3.2 迭代器使用)

[5.1.3.3 容量操作](#5.1.3.3 容量操作)

[5.1.3.4 元素访问](#5.1.3.4 元素访问)

[5.1.3.5 修改操作](#5.1.3.5 修改操作)

[5.1.3.6 list特有操作](#5.1.3.6 list特有操作)

[5.1.4 deque](#5.1.4 deque)

[5.1.5 序列式容器对比](#5.1.5 序列式容器对比)

[5.2 关联式容器](#5.2 关联式容器)

有序关联容器（基于红黑树）

无序关联容器（基于哈希表，C++11）

[5.2.1 set](#5.2.1 set)

[5.2.1.1 构造set](#5.2.1.1 构造set)

[5.2.1.2 set的迭代器](#5.2.1.2 set的迭代器)

[5.2.1.3 set的增删查操作](#5.2.1.3 set的增删查操作)

[5.2.2 map](#5.2.2 map)

[5.2.2.1 构造map](#5.2.2.1 构造map)

[5.2.2.2 map的迭代器](#5.2.2.2 map的迭代器)

[5.2.2.3 map的operator[]](#5.2.2.3 map的operator[])

[5.3 容器适配器](#5.3 容器适配器)

[5.3.1 容器适配器的概念](#5.3.1 容器适配器的概念)

核心特点：

[5.3.2 STL中的三种容器适配器](#5.3.2 STL中的三种容器适配器)

[5.3.2.1 stack](#5.3.2.1 stack)

[5.3.2.2 queue](#5.3.2.2 queue)

[5.3.2.3 priority_queue](#5.3.2.3 priority_queue)

[6. STL的迭代器](#6. STL的迭代器)

6.1迭代器分类

[6.2 迭代器的基本使用](#6.2 迭代器的基本使用)

[6.2.1 获取迭代器](#6.2.1 获取迭代器)

[6.2.2 遍历容器](#6.2.2 遍历容器)

[6.2.3 迭代器操作](#6.2.3 迭代器操作)

[6.3 迭代器失效问题](#6.3 迭代器失效问题)

[6.3.1 各容器迭代器失效情况](#6.3.1 各容器迭代器失效情况)

[vector 和 string](#vector 和 string)

[list 和 forward_list](#list 和 forward_list)

[关联容器（set, map, multiset, multimap）](#关联容器（set, map, multiset, multimap）)

[6.3.2 避免迭代器失效的策略](#6.3.2 避免迭代器失效的策略)

修改之后重新获得迭代器

索引代替迭代器

先计算再修改

上一篇:从零开始的C++学习生活 19:C++复习课(5.4w字全解析)-CSDN博客

前言

这是C++的最后一课，复习我们所学的数据结构和C++中的STL

数据结构与STL（标准模板库）是计算机科学的核心基础，它们共同构成了高效程序设计的重要支柱。数据结构提供了组织和管理数据的方法，而STL则为我们提供了现成的、经过优化的数据结构和算法实现。

那么就让我带你们最后一程，系统性地复习常见数据结构的基本概念、实现原理，以及STL中对应容器的使用方法和内部机制。结束C++的最后一舞

1. 复杂度计算

1.1 什么是算法复杂度？

算法复杂度 是衡量算法效率的数学工具，主要用于分析算法在时间 和空间方面的资源消耗如何随着输入规模的增长而变化。

1.2 复杂度的类型

1. 时间复杂度

衡量算法运行时间与输入规模的关系。

2. 空间复杂度

衡量算法内存使用量与输入规模的关系。

大O表示法

大O表示法描述算法的最坏情况下的复杂度增长趋势。

1.3 常见的时间复杂度

1.3.1 常数时间复杂度

一般情况下，没有未知数N的干扰，而是已知的某个常数下的执行次数，那么就是O(1)

cpp 复制代码 
// O(1) - 常数时间复杂度
void constantTime() {
    cout << "=== O(1) 常数时间复杂度 ===" << endl;
    
    vector<int> arr = {1, 2, 3, 4, 5};
    
    // 无论数组多大，这些操作都只执行一次
    if (!arr.empty()) {
        cout << "第一个元素: " << arr[0] << endl;  // O(1)
    }
    
    arr.push_back(6);  // 平均情况下 O(1)
    
    int a = 10, b = 20;
    int sum = a + b;  // O(1)
    
    cout << "特点：执行时间不随输入规模变化" << endl;
}

1.3.2 对数时间复杂度

有未知数N的干扰，以2的N次方等于某一个常数，那么就是O(logN)

其中二分查找和搜索二叉树就是典型的O(logN)

cpp 复制代码 
// O(log n) - 对数时间复杂度
void Time() {
    cout << "\n=== O(log n) 对数时间复杂度 ===" << endl;
    
    vector<int> sorted_arr = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19};
    int target = 13;
    
    // 二分查找 - O(log n)
    auto binarySearch = [](const vector<int>& arr, int target) {
        int left = 0, right = arr.size() - 1;
        int steps = 0;
        
        while (left <= right) {
            steps++;
            int mid = left + (right - left) / 2;
            
            if (arr[mid] == target) {
                cout << "找到目标 " << target << ", 步骤数: " << steps << endl;
                return mid;
            } else if (arr[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        
        cout << "未找到目标, 步骤数: " << steps << endl;
        return -1;
    };
    
    binarySearch(sorted_arr, target);
    cout << "输入规模: " << sorted_arr.size() << ", 最大步骤: log₂(" 
         << sorted_arr.size() << ") ≈ " << log2(sorted_arr.size()) << endl;
}

1.3.3 线性时间复杂度

有未知数N的干扰，且一般以N为一个循环，那么就是O(N)

cpp 复制代码 
// O(n) - 线性时间复杂度
void Time() {
    cout << "\n=== O(n) 线性时间复杂度 ===" << endl;
    
    vector<int> arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    
    cin>>n;
    auto it = arr.begin();
    while(it!=arr.end())//最坏情况:找到的数字为最后一个
    {
        if(*it == n)
        {
            cout<<"找到了"<<endl;
        }
        it++;
    }
}

1.3.4 线性对数时间复杂度

常见的很多排序算法的时间复杂度就是线性对数时间复杂度

cpp 复制代码 
// O(n log n) - 线性对数时间复杂度
void linearithmicTime() {
    cout << "\n=== O(n log n) 线性对数时间复杂度 ===" << endl;
    
    vector<int> arr = {9, 5, 7, 1, 3, 8, 2, 6, 4, 10};
    
    cout << "排序前: ";
    for (int num : arr) cout << num << " ";
    cout << endl;
    
    // 快速排序、归并排序的平均情况 - O(n log n)
    sort(arr.begin(), arr.end());
    
    cout << "排序后: ";
    for (int num : arr) cout << num << " ";
    cout << endl;
    
    cout << "输入规模: " << arr.size() 
         << ", 复杂度: O(" << arr.size() << " log " << arr.size() << ")" << endl;
}

1.3.5 平方时间复杂度

两个带N循环叠加在一起就是平方时间复杂度

cpp 复制代码 
// O(n²) - 平方时间复杂度
void quadraticTime() {
    cout << "\n=== O(n²) 平方时间复杂度 ===" << endl;
    
    vector<int> arr = {1, 2, 3, 4, 5};
    
    // 冒泡排序 - O(n²)
    auto bubbleSort = [](vector<int> arr) {
        int n = arr.size();
        int steps = 0;
        
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                steps++;
                if (arr[j] > arr[j + 1]) {
                    swap(arr[j], arr[j + 1]);
                }
            }
        }
        
        cout << "排序步骤数: " << steps << endl;
        cout << "理论最大步骤: n² = " << n * n << endl;
        return arr;
    };
    
    auto sorted = bubbleSort(arr);
}

1.4 常见的空间复杂度

空间复杂度一般指开辟空间的多少

1.4.1 O(1)空间复杂度

cpp 复制代码 
// O(1) 空间复杂度
    auto constantSpace = [](const vector<int>& arr) {
        int sum = 0;           // 1个变量
        for (int num : arr) {
            sum += num;        // 只使用固定数量的变量
        }
        return sum;
    };

1.4.2 O(N)空间复杂度

cpp 复制代码 
 auto linearSpace = [](const vector<int>& arr) {
        vector<int> copy = arr;  // 创建与输入相同大小的副本
        // 还可能有其他O(1)的变量
        return copy.size();
    };

1.4.3 O(N^2)空间复杂度

cpp 复制代码 
// O(n²) 空间复杂度
    auto quadraticSpace = [](int n) {
        vector<vector<int>> matrix(n, vector<int>(n));  // n x n 矩阵
        return matrix.size();
    };

1.5 复杂度的主要作用

由于现代内存较之前来说已经十分便宜了，16GB甚至是32GB十分常见，因此我们对于空间复杂度的要求并不高，而是要求高效的时间复杂度

时间复杂度越低，代码质量越高

对于时间复杂度也有以下作用:

  1. 算法比较 - 客观比较不同算法的效率

  2. 性能预测 - 预估算法在不同规模数据下的表现

  3. 系统设计 - 指导选择合适的算法和数据结构

  4. 问题分析 - 理解问题的本质难度

  5. 优化方向 - 识别性能瓶颈和改进空间

2. 线性数据结构

线性数据结构，一般指在逻辑结构上各个元素成线性排列，而不是物理层面上

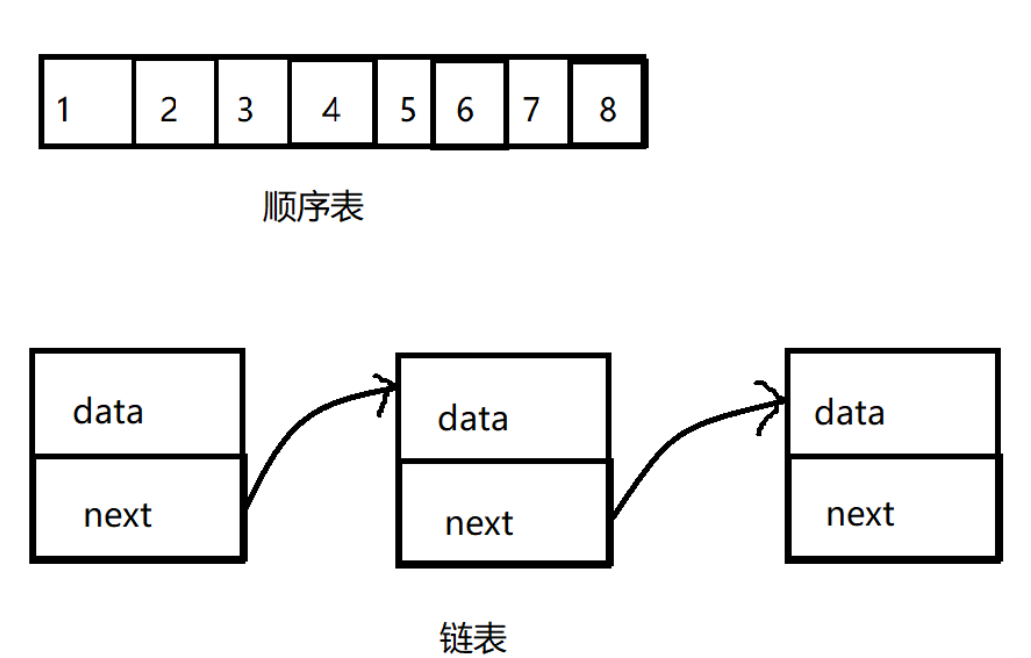
顺序表不仅逻辑结构还是物理结构都是绝对的线性

但是链表虽然物理上不是，但是在逻辑上可以看作是一条绳子拴在一起，呈线性，仍然是线性数据结构

同样的，栈和队列也是线性的

关于模拟实现，我们只用关注最核心的增删查改即可

2.1 顺序表

顺序表其实就是数组

其具有以下特性

  • 连续内存：元素在内存中连续存储

  • 随机访问：通过索引直接访问任何元素

  • 固定大小：创建时确定大小（静态数组）

当然，我们都到数据结构了，当然不可能用静态数组这么个低端的玩具。我们当然是用动态数组->即内存动态开辟的数组

cpp 复制代码 
class MyArray {
private:
    T* data;           // 指向数组的指针
    size_t capacity;   // 数组容量
    size_t length;     // 当前元素数量
    //......
}

增

cpp 复制代码 
// 添加元素
    void push_back(const T& value) {
        if (length >= capacity) {
            resize(capacity * 2);  // 容量不足时翻倍
        }
        data[length++] = value;
    }
cpp 复制代码 
 // 在指定位置插入元素
    void insert(size_t index, const T& value) {
        if (index > length) {
            throw out_of_range("索引越界");
        }
        
        if (length >= capacity) {
            resize(capacity * 2);
        }
        
        // 后移元素
        for (size_t i = length; i > index; i--) {
            data[i] = data[i - 1];
        }
        
        data[index] = value;
        length++;
    }

删

cpp 复制代码 
// 删除末尾元素
    void pop_back() {
        if (length > 0) {
            length--;
        }
    }
 // 删除指定位置元素
    void erase(size_t index) {
        if (index >= length) {
            throw out_of_range("索引越界");
        }
        
        // 前移元素
        for (size_t i = index; i < length - 1; i++) {
            data[i] = data[i + 1];
        }
        
        length--;
    }

查

cpp 复制代码 
// 查找元素
    int find(const T& value) const {
        for (size_t i = 0; i < length; i++) {
            if (data[i] == value) {
                return i;
            }
        }
        return -1;
    }

2.2 链表

链表最大的特性即"串起来"，用指针串

  • 节点结构：每个节点包含数据和指向下一个节点的指针

  • 动态内存：不需要连续内存空间

  • 灵活大小：可以动态添加/删除节点

模拟实现（单向链表）

cpp 复制代码 
class SinglyLinkedList {
private:
    // 节点定义
    struct Node {
        T data;
        Node* next;
        Node(const T& value) : data(value), next(nullptr) {}
    };
    
    Node* head;    // 头节点
    Node* tail;    // 尾节点
    size_t size;   // 链表大小
    /......
}

增

cpp 复制代码 
// 在头部添加元素
    void push_front(const T& value) {
        Node* newNode = new Node(value);
        if (head == nullptr) {
            head = tail = newNode;
        } else {
            newNode->next = head;
            head = newNode;
        }
        size++;
    }
 // 在指定位置插入
    void insert(size_t index, const T& value) {
        if (index > size) {
            throw out_of_range("索引越界");
        }
        
        if (index == 0) {
            push_front(value);
        } else if (index == size) {
            push_back(value);
        } else {
            Node* newNode = new Node(value);
            Node* current = head;
            
            for (size_t i = 0; i < index - 1; i++) {
                current = current->next;
            }
            
            newNode->next = current->next;
            current->next = newNode;
            size++;
        }
    }

删

cpp 复制代码 
// 删除指定位置元素
    void erase(size_t index) {
        if (index >= size) {
            throw out_of_range("索引越界");
        }
        
        if (index == 0) {
            pop_front();
        } else {
            Node* current = head;
            for (size_t i = 0; i < index - 1; i++) {
                current = current->next;
            }
            
            Node* toDelete = current->next;
            current->next = toDelete->next;
            
            if (toDelete == tail) {
                tail = current;
            }
            
            delete toDelete;
            size--;
        }
    }

查

cpp 复制代码 
 // 查找元素
    int find(const T& value) const {
        Node* current = head;
        int index = 0;
        
        while (current != nullptr) {
            if (current->data == value) {
                return index;
            }
            current = current->next;
            index++;
        }
        return -1;
    }

2.3 栈

栈是一种特殊的线性表，只允许在固定的一端进行插入和删除操作。这一端称为栈顶 ，另一端称为栈底 。栈遵循后进先出（LIFO, Last In First Out）原则。

  • 压栈/入栈：向栈中插入新元素的操作

  • 出栈：从栈中删除元素的操作

我们可以简单想象成一个桶，开口在上，我们取物品当然只能从最上面开始拿，直到底部

因此最先放进去的物品在最底部，也是最后拿；最后放进去的物品在最上面，也是最先拿

栈就是类似于这样一个东西

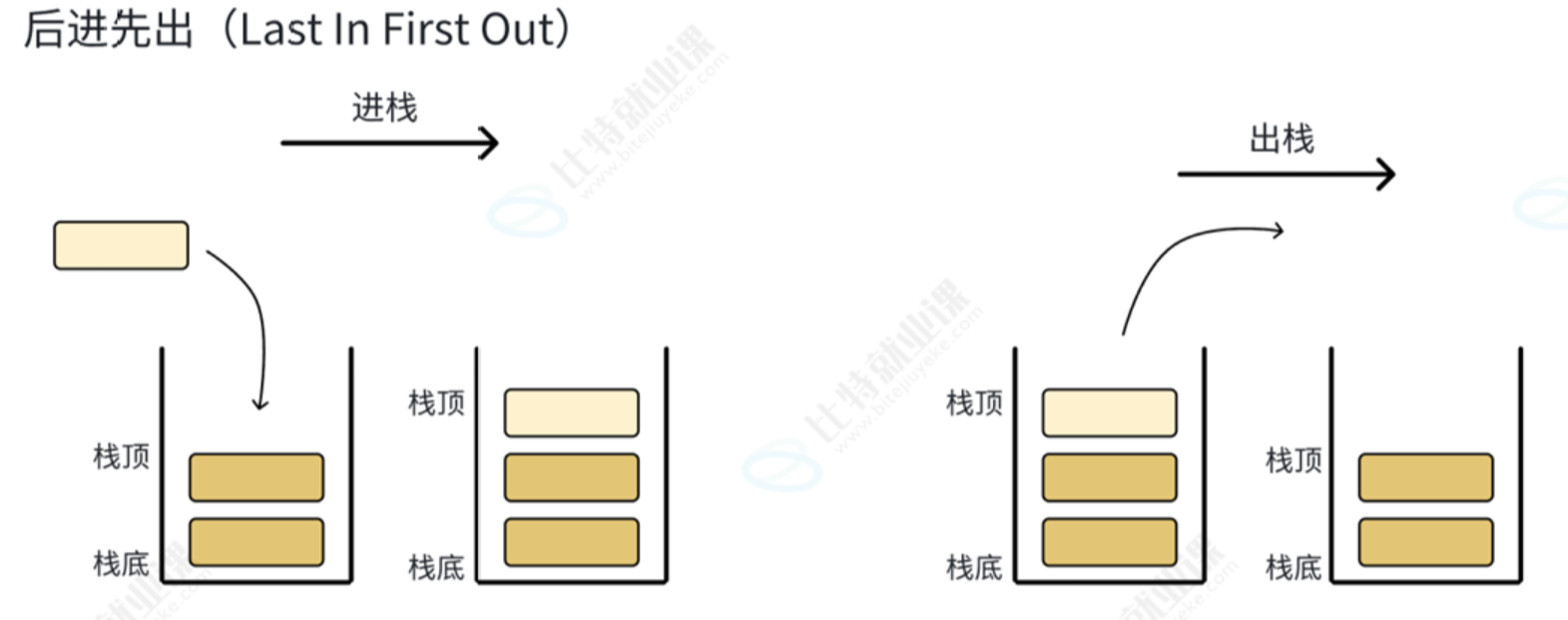
栈的底层结构选择

栈可以使用数组或链表实现。这里我选择链表来实现

cpp 复制代码 
class Stack {
private:
    struct Node {
        T data;
        Node* next;
        Node(const T& value) : data(value), next(nullptr) {}
    };
    
    Node* topNode;
    size_t stackSize;
    /......
}

压栈

cpp 复制代码 
// 入栈
    void push(const T& value) {
        Node* newNode = new Node(value);
        newNode->next = topNode;
        topNode = newNode;
        stackSize++;
    }

出栈

cpp 复制代码 
// 入栈
    void push(const T& value) {
        Node* newNode = new Node(value);
        newNode->next = topNode;
        topNode = newNode;
        stackSize++;
    }

获取栈顶元素

cpp 复制代码 
// 获取栈顶元素
    T& top() {
        if (empty()) {
            throw runtime_error("栈为空");
        }
        return topNode->data;
    }
    
    const T& top() const {
        if (empty()) {
            throw runtime_error("栈为空");
        }
        return topNode->data;
    }

2.4 队列

队列是一种特殊的线性表，只允许在一端进行插入操作（队尾），在另一端进行删除操作（队头）。队列遵循先进先出（FIFO, First In First Out）原则。

入队列：在队尾插入元素

出队列：在队头删除元素

我们可以想象成在排队，队伍前面的人当然先走，队伍后面的人得一直等，和栈是相反的概念

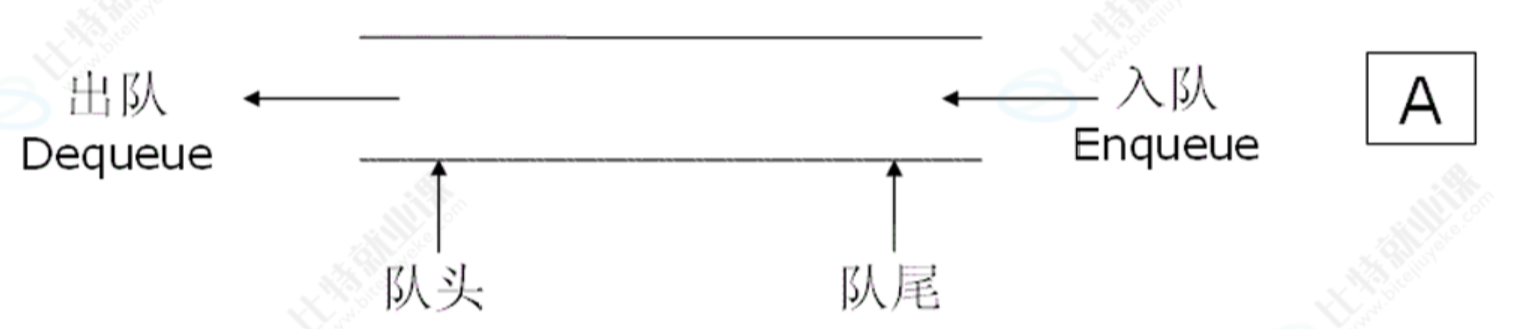
队列的底层结构选择

队列可以使用数组或链表实现。这里我选择链表来实现

cpp 复制代码 
class Queue {
private:
    struct Node {
        T data;
        Node* next;
        Node(const T& value) : data(value), next(nullptr) {}
    };
    
    Node* frontNode;
    Node* rearNode;
    size_t queueSize;
    //......
}

入队

cpp 复制代码 
 // 入队
    void enqueue(const T& value) {
        Node* newNode = new Node(value);
        
        if (rearNode == nullptr) {
            frontNode = rearNode = newNode;
        } else {
            rearNode->next = newNode;
            rearNode = newNode;
        }
        queueSize++;
    }

出队

cpp 复制代码 
 // 出队
    void dequeue() {
        if (empty()) {
            throw runtime_error("队列为空");
        }
        
        Node* temp = frontNode;
        frontNode = frontNode->next;
        
        if (frontNode == nullptr) {
            rearNode = nullptr;
        }
        
        delete temp;
        queueSize--;
    }

获取队头数据

cpp 复制代码 
// 获取队头元素
    T& front() {
        if (empty()) {
            throw runtime_error("队列为空");
        }
        return frontNode->data;
    }
    
    const T& front() const {
        if (empty()) {
            throw runtime_error("队列为空");
        }
        return frontNode->data;
    }

3. 非线性数据结构

非线性数据结构在逻辑层面上不呈线性，因此是非线性

典型的有树和哈希

虽然哈希表在底层中是数组，物理层面是线性的，但在理论层面我们仍认为是非线性的

3.1 树

3.1.1 树的概念

树是一种非线性数据结构，由n(n>0)个有限节点组成一个具有层次关系的集合。它看起来像一棵倒挂的树，根朝上，叶朝下。

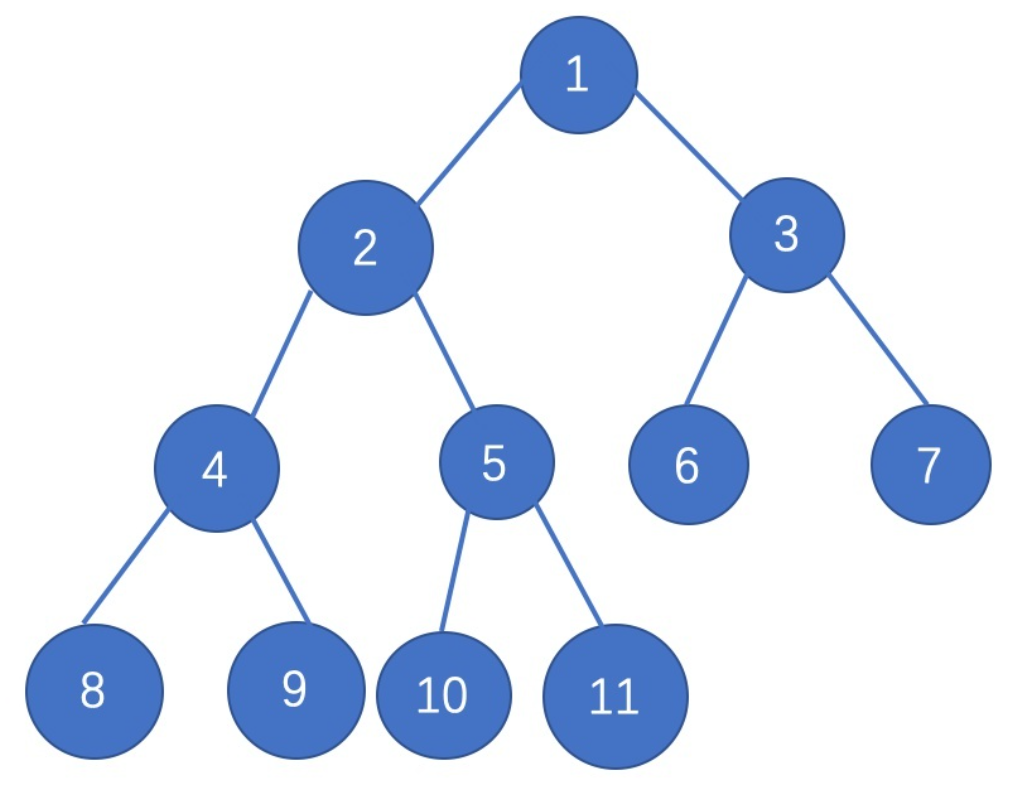
树的核心特性：

  • 有一个特殊的根节点，没有前驱节点

  • 除根节点外，其余节点被分成M(M>0)个互不相交的集合T₁, T₂, ..., Tₘ

  • 每个子集Tᵢ又是一棵结构与树类似的子树

注意:在树形结构中,子树之间不能有交集，否则就不是树形结构

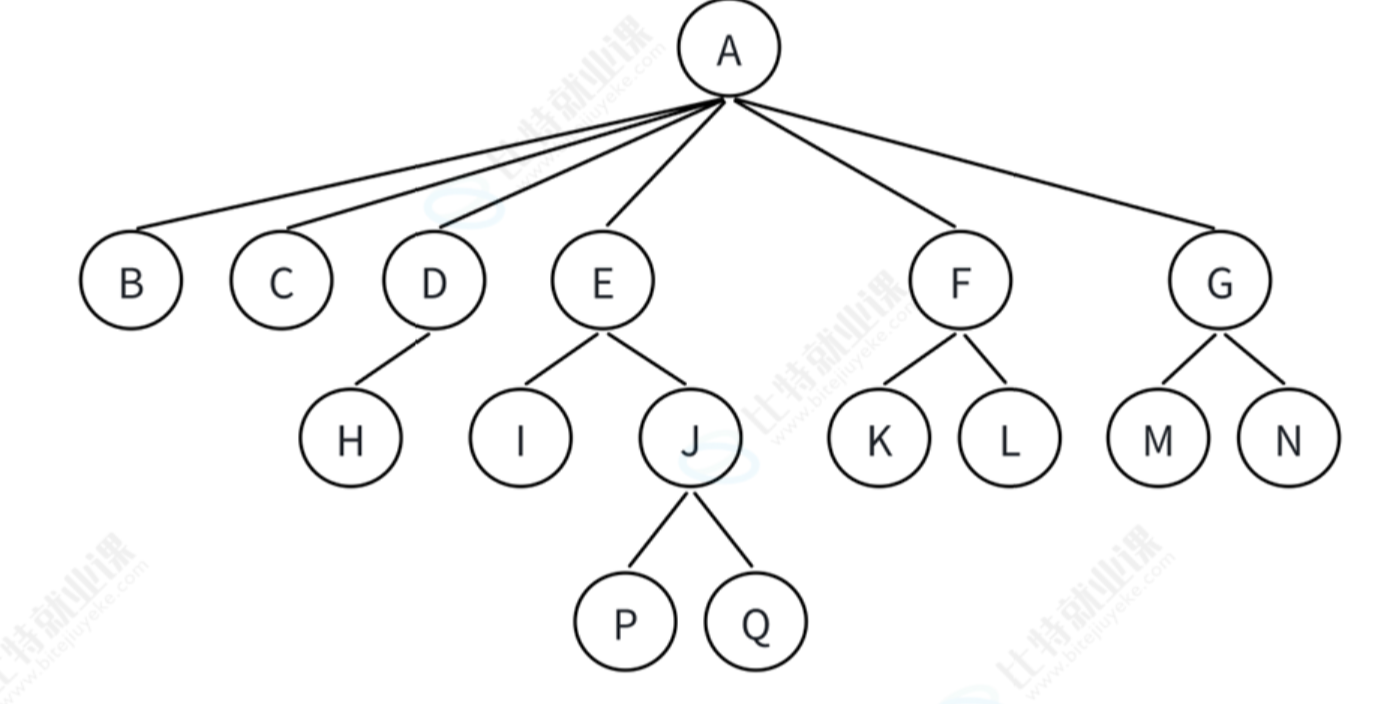
3.1.2 树的常见术语和表示

常见术语

  • 父节点/双亲节点：含有子节点的节点（如A是B的父节点）

  • 子节点/孩子节点：一个节点含有的子树的根节点（如B是A的孩子节点）

  • 节点的度：节点拥有的子树个数（如A的度为6，B的度为0）

  • 树的度：树中所有节点的度的最大值

  • 叶节点：度为0的节点（如H、B、P）

  • 分支节点：度不为0的节点

  • 兄弟节点：具有相同父节点的节点（如B、C、D是兄弟节点）

  • 节点的层次：从根开始，根为第1层，依次递增

  • 树的高度：树中节点的最大层次

  • 路径：从树中任意节点出发，沿父节点-子节点连接达到任意节点的序列

树的表示

我们通过上述的图片可以发现，树的逻辑结构很像链表，无非是多个节点通过链表相互连接，同时具有一定的关系，因此我们以下用链表来建造树

左孩子和右孩子表示法

cpp 复制代码 
typedef int BTDataType;

typedef struct BinaryTreeNode {
    struct BinaryTreeNode* left;   // 左孩子指针
    struct BinaryTreeNode* right;  // 右孩子指针
    BTDataType data;               // 数据域
} BTNode;

左孩子和右孩子顾名思义，即为一个节点的左下的节点和右下的节点

在上图中A的左孩子为B,右孩子为C

data为该节点存储的值

左孩子和右兄弟表示法

cpp 复制代码 
 struct TreeNode 
{ 
   struct Node* leftchild;   // 左边开始的第⼀个孩⼦结点
   struct Node* rightbrother; // 指向其右边的下⼀个兄弟结点
   int data;// 结点中的数据域     
};

该表示法把右孩子改成了右兄弟，如B的右兄弟为C

3.2 二叉树

二叉树是节点的有限集合，该集合：

  • 或者为空

  • 或者由一个根节点加上两棵分别称为左子树和右子树的二叉树组成

3.2.1 二叉树的种类

满二叉树

每一层的节点数都达到最大值。如果层数为K，则节点总数为2ᴷ - 1。

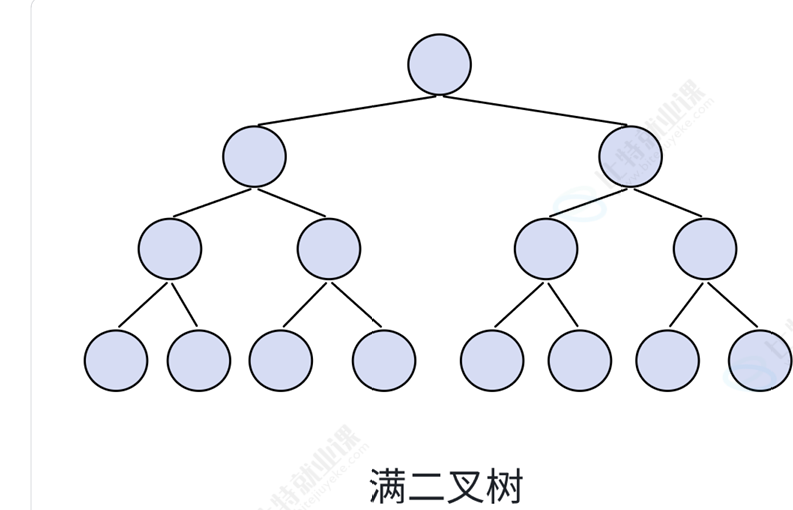
完全二叉树

深度为K，有n个节点的二叉树，当且仅当其每一个节点都与深度为K的满二叉树中编号从1到n的节点一一对应。

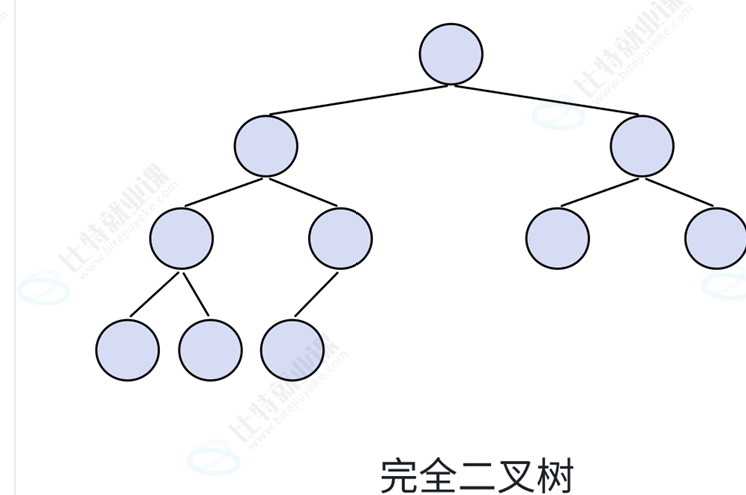
完全二叉树中每个层级的节点必须得以从左到右分布，如果中间有空，而右边蹦出了一个节点就不算完全二叉树

3.2.2 堆

3.2.2.1 堆的概念

堆是一种特殊的完全二叉树，满足：

  • 大堆：每个节点的值都大于或等于其子节点的值

  • 小堆：每个节点的值都小于或等于其子节点的值

可以看出，堆一定是个完全二叉树。大堆可以看作从大到小排，但如果以每一层的从左到右看不一定都从大到小，只是在竖直方向上保持，即父亲节点的值一定大于儿子节点的值，但儿子节点之间的值不一定从左到右，从大到小排序。小堆即相反。

3.2.2.2 数组实现堆的基础结构

由于堆是个完全二叉树，我们可以使用顺序表来实现

那么如果把堆的节点存储在数组中?

可以从上到下，从左到右以序号来存储

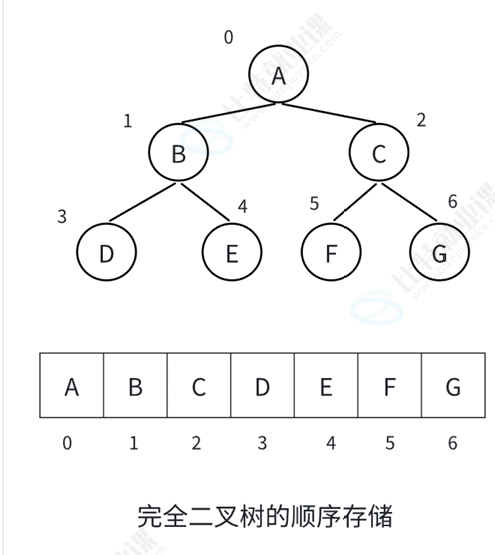
我们把堆的根-A放在数组下标为0的位置，那么B和C理所当然分别为1和2，那么DEFG如何确定序号?

因为堆的性质可以利用等比数列来求，我们可以发现当根的序号为i时，两个子节点的序号分别为2i+1和2i+2，反过来也可也利用子节点的序号来推导根的序号

3.2.2.3 堆的创建与销毁
cpp 复制代码 
typedef int HPDataType;

typedef struct Heap {
    HPDataType* data;    // 存储数据的数组
    int size;           // 当前元素个数
    int capacity;       // 容量
} HP;

// 堆的初始化
void HeapInit(HP* hp) {
    hp->data = NULL;
    hp->size = hp->capacity = 0;
}

// 堆的销毁
void HeapDestroy(HP* hp) {
    free(hp->data);
    hp->data = NULL;
    hp->size = hp->capacity = 0;
}
cpp 复制代码 
void HPPush(HP* php, HPDataType x)
 {
    assert(php);
    if (php->size == php->capacity)
    {
        size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
        HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);
        if (tmp == NULL)
        {
            perror("realloc fail");
            return;
        }
        php->a = tmp;
        php->capacity = newCapacity;
    }
    php->a[php->size] = x;
    php->size++;
    AdjustUp(php->a, php->size-1);
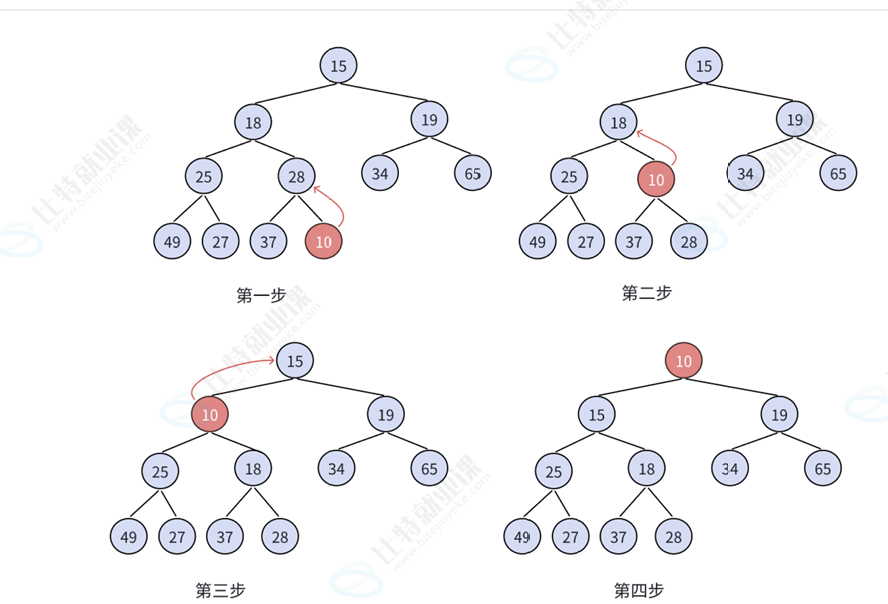
 }//堆节点的引入
3.2.2.4 向上调整算法

如果我们要创造一个小堆或者大堆，那么就必须对根和子节点进行交换，以保持从大到小或从小到大的序列

cpp 复制代码 
void AdjustUp(HPDataType* data, int child) {
    int parent = (child - 1) / 2;
    
    while (child > 0) {
        // 大堆：data[child] > data[parent]
        // 小堆：data[child] < data[parent]
        if (data[child] > data[parent]) {
            // 交换父子节点
            HPDataType temp = data[child];
            data[child] = data[parent];
            data[parent] = temp;
            
            // 向上继续调整
            child = parent;
            parent = (child - 1) / 2;
        } else {
            break;
        }
    }
}

在上述算法中，我们先选取一个子节点，找到他的根，随后进行大小的排序。

一个结构排完后，再继续向上排

3.2.2.5 向下调整算法

删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

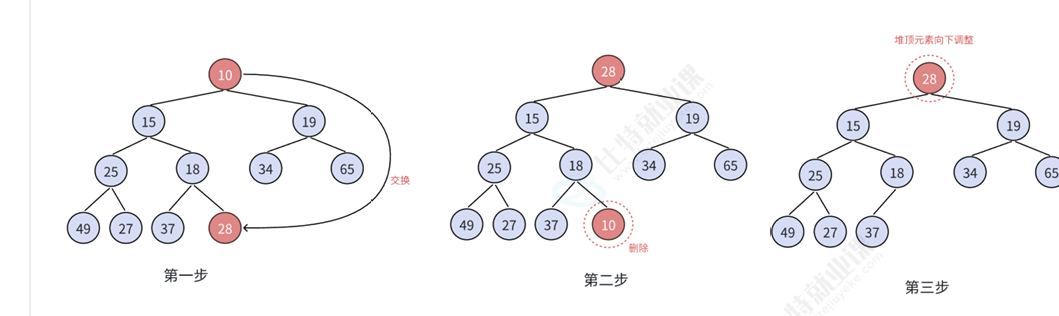
向下调整算法有一个前提：左右子树必须是⼀个堆，才能调整

cpp 复制代码 
void AdjustDown(HPDataType* data, int n, int parent) {
    int child = parent * 2 + 1; // 左孩子
    
    while (child < n) {
        // 选出左右孩子中较大的（大堆）
        if (child + 1 < n && data[child + 1] > data[child]) {
            child++;
        }
        
        // 如果孩子大于父亲，需要调整
        if (data[child] > data[parent]) {
            HPDataType temp = data[child];
            data[child] = data[parent];
            data[parent] = temp;
            
            parent = child;
            child = parent * 2 + 1;
        } else {
            break;
        }
    }
}
cpp 复制代码 
void HPPop(HP* php)
 {
    assert(php);
    assert(php->size > 0);
    Swap(&php->a[0], &php->a[php->size - 1]);
    php->size--;
    AdjustDown(php->a, php->size, 0);//删除堆顶数据时自动排序
 }
3.2.2.6 堆排序

当我们有一些无序的数据时，可以把他们放进堆中，制造一个小堆或者大堆，再对除最后一层外的所有节点进行向下调整算法，可以得到一个完全升序或者降序的堆

cpp 复制代码 
void HeapSort(int* arr, int n) {
    // 建堆：从最后一个非叶子节点开始向下调整
    for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
        AdjustDown(arr, n, i);
    }
    
    // 排序：将堆顶元素与末尾交换，然后调整堆
    int end = n - 1;
    while (end > 0) {
        // 交换堆顶和末尾元素
        int temp = arr[0];
        arr[0] = arr[end];
        arr[end] = temp;
        
        // 调整堆
        AdjustDown(arr, end, 0);
        end--;
    }
}

该版本有一个前提，必须提供有现成的数据结构堆

3.2.2.7 TOP-K问题

假设有一串数据，我要你找到前K个最大或者前K个最小的数据?

我们可以建造一个含K个节点的小堆或者大堆，如果是前K个最大，可建造小堆，这时堆顶一定是堆中最小的数据，如果遇到了比更大的数据，那么把该数据置换到对顶中，以此到最后堆中一i的那个是前K个最大的数据。前K个最小则相反

cpp 复制代码 
void PrintTopK(int* arr, int n, int k) {
    // 用前K个元素建小堆
    for (int i = (k - 1 - 1) / 2; i >= 0; i--) {
        AdjustDown(arr, k, i);
    }
    
    // 遍历剩余元素
    for (int i = k; i < n; i++) {
        if (arr[i] > arr[0]) {
            arr[0] = arr[i];
            AdjustDown(arr, k, 0);
        }
    }
    
    // 输出前K个最大的元素
    for (int i = 0; i < k; i++) {
        printf("%d ", arr[i]);
    }
}

3.3 二叉搜索树

二叉搜索树极其重要，因此我们专门开一个板块

3.3.1 二叉搜索树的概念

二叉搜索树（Binary Search Tree）是一种特殊的二叉树，它具有以下性质：

  • 若左子树不为空，则左子树上所有节点的值都小于等于根节点的值

  • 若右子树不为空，则右子树上所有节点的值都大于等于根节点的值

  • 左右子树也都是二叉搜索树

这种有序性使得我们能够高效地进行查找、插入和删除操作。

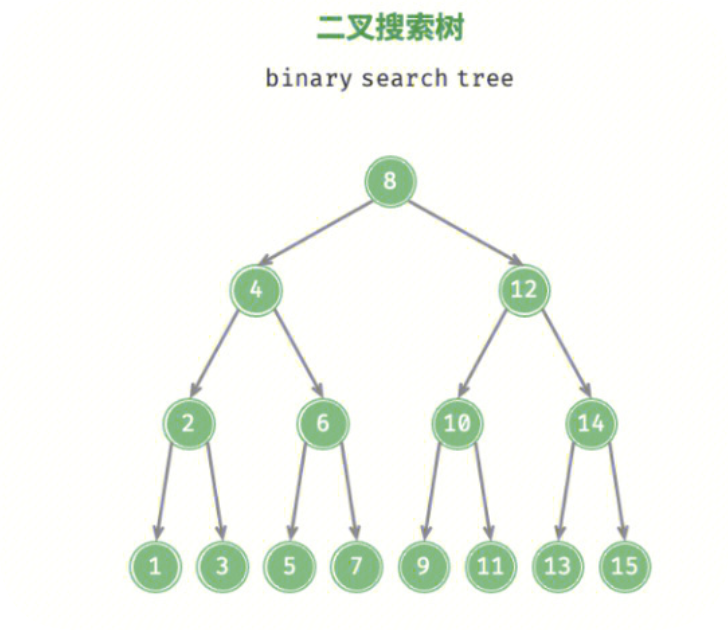
3.3.2 二叉搜索树的性能分析

最优情况下，二叉搜索树为完全二叉树(或者接近完全二叉树)，其高度为： log2 N 最差情况下，二叉搜索树退化为单支树(或者类似单支)，其高度为： N 所以综合而言二叉搜索树增删查改时间复杂度为： O(N)

另外需要说明的是，二分查找也可以实现级别的查找效率，但是二分查找有两大缺陷：

  1. 需要存储在支持下标随机访问的结构中，并且有序。

  2. 插入和删除数据效率很低，因为存储在下标随机访问的结构中，插入和删除数据⼀般需要挪动数 据。

这里也就体现出了平衡二叉搜索树的价值。

  • 动态性能：支持高效的动态插入和删除

  • 有序存储：数据自然有序，便于范围查询

  • 灵活扩展：可以轻松扩展为更复杂的平衡树结构

3.3.3 构建基础二叉搜索树

3.3.3.1 查找

查找是二叉搜索树最基本的操作

  1. 从根开始比较，查找x，x比根的值大则往右边走查找，x比根值小则往左边走查找

  2. 最多查找高度次，走到到空，还没找到，这个值不存在

  3. 如果不支持插入相等的值，找到x即可返回

  4. 如果支持插入相等的值，意味着有多个x存在，一般要求查找中序的第一个x

cpp 复制代码 
bool Find(const K& key) {
    Node* cur = _root;
    while (cur) {
        if (cur->_key < key) {
            cur = cur->_right;  // 在右子树中查找
        } else if (cur->_key > key) {
            cur = cur->_left;   // 在左子树中查找
        } else {
            return true;        // 找到目标
        }
    }
    return false;               // 未找到
}

cur有两种情况:

  1. 没有找到，cur为空指针->退出循环，返回false

  2. 找到了，返回true

时间复杂度：

  • 最好情况：O(log n) - 树完全平衡时

  • 最坏情况：O(n) - 树退化为链表时

3.3.3.2 插入

插入操作需要保持二叉搜索树的性质：

  • 若左子树不为空，则左子树上所有节点的值都小于等于根节点的值

  • 若右子树不为空，则右子树上所有节点的值都大于等于根节点的值

因此我们分以下情况:

  1. 树为空，即根节点都不存在，那么直接把插入的节点当作根节点
  2. 树不空，按二叉搜索树性质，插入值比当前结点大往右走，插入值比当前结点小往左走，找到空位置，插入新结点。
  3. 如果支持插入相等的值，插入值跟当前结点相等的值可以往右走，也可以往左走，找到空位置，插入新结点
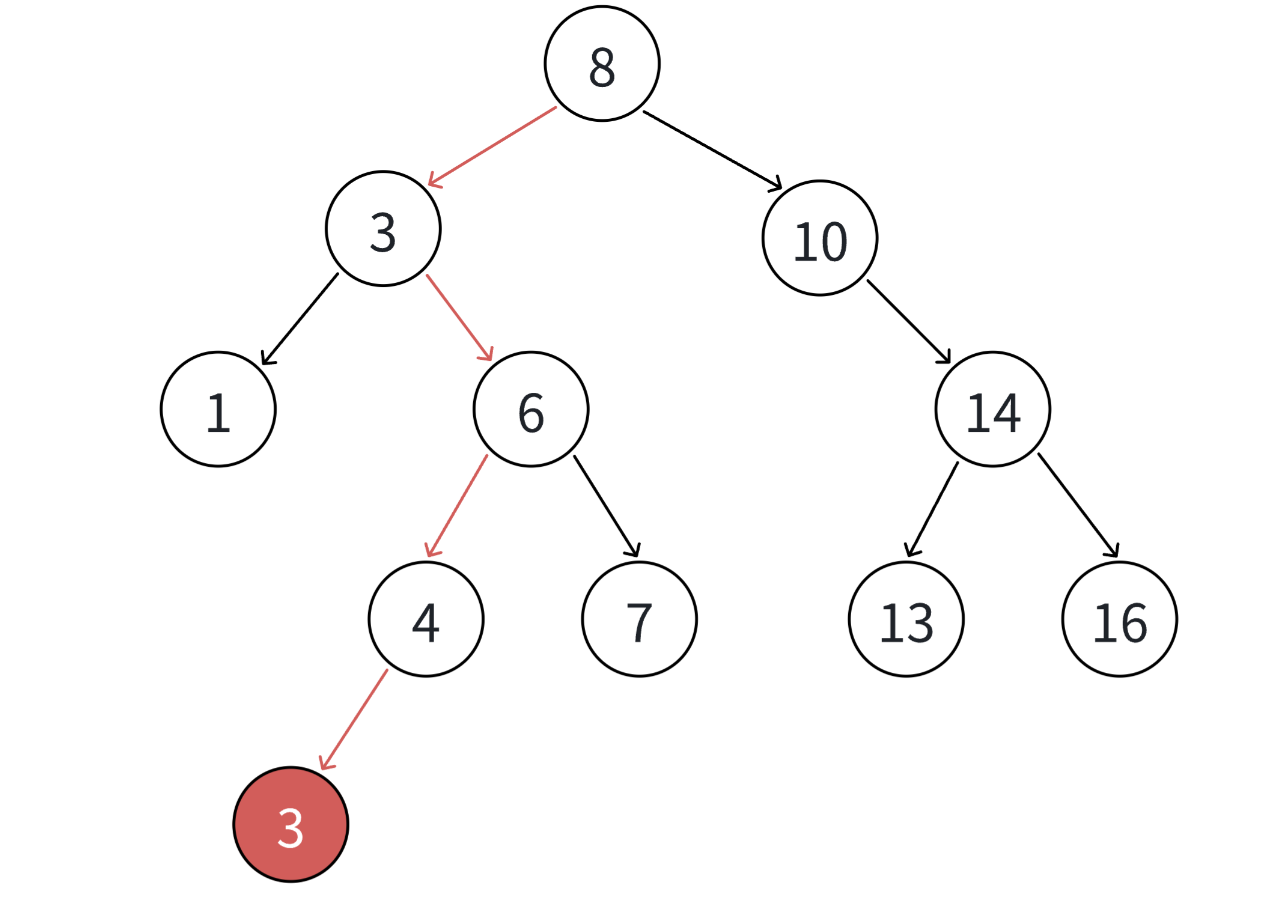
cpp 复制代码 
bool Insert(const K& key) {
    if (_root == nullptr) {//树为空
        _root = new Node(key);
        return true;
    }
    
    Node* parent = nullptr;
    Node* cur = _root;
    
    // 寻找插入位置
    while (cur) {
        parent = cur;
        if (cur->_key <= key) {
            cur = cur->_right;
        } 
        else{
            cur = cur->_left;
        }
    }
    
    // 创建新节点并插入
    cur = new Node(key);
    if (parent->_key < key) {
        parent->_right = cur;
    } else {
        parent->_left = cur;
    }
    
    return true;
}
3.3.3.3 删除

首先查找元素是否在二叉搜索树中，如果不存在，则返回false。

如果查找元素存在则分以下四种情况分别处理：（假设要删除的结点为N）

  1. 要删除结点N左右孩子均为空
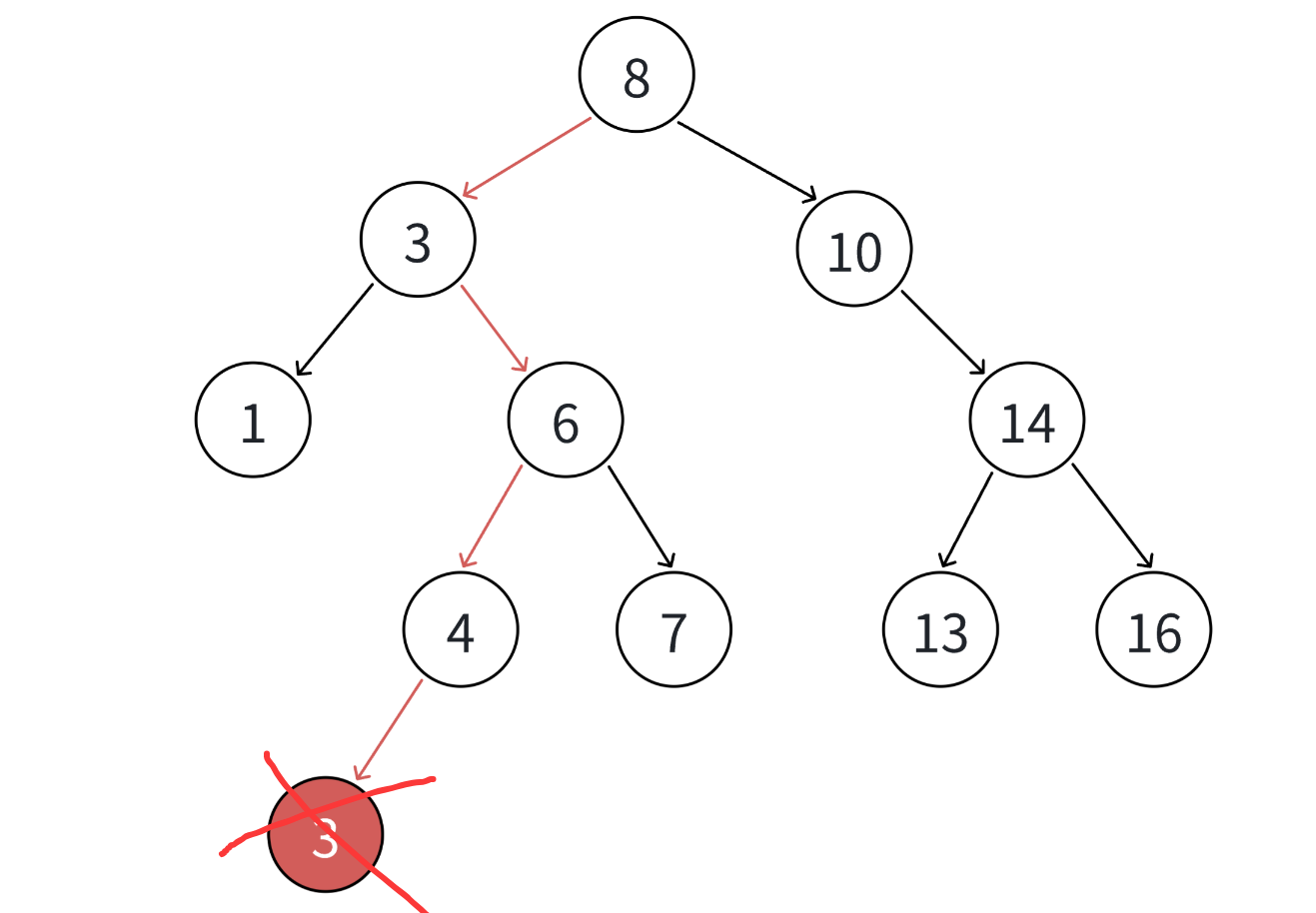
  1. 要删除的结点N左孩子为空，右孩子结点不为空，那么删除节点的父节点则应该指向删除节点的右孩子
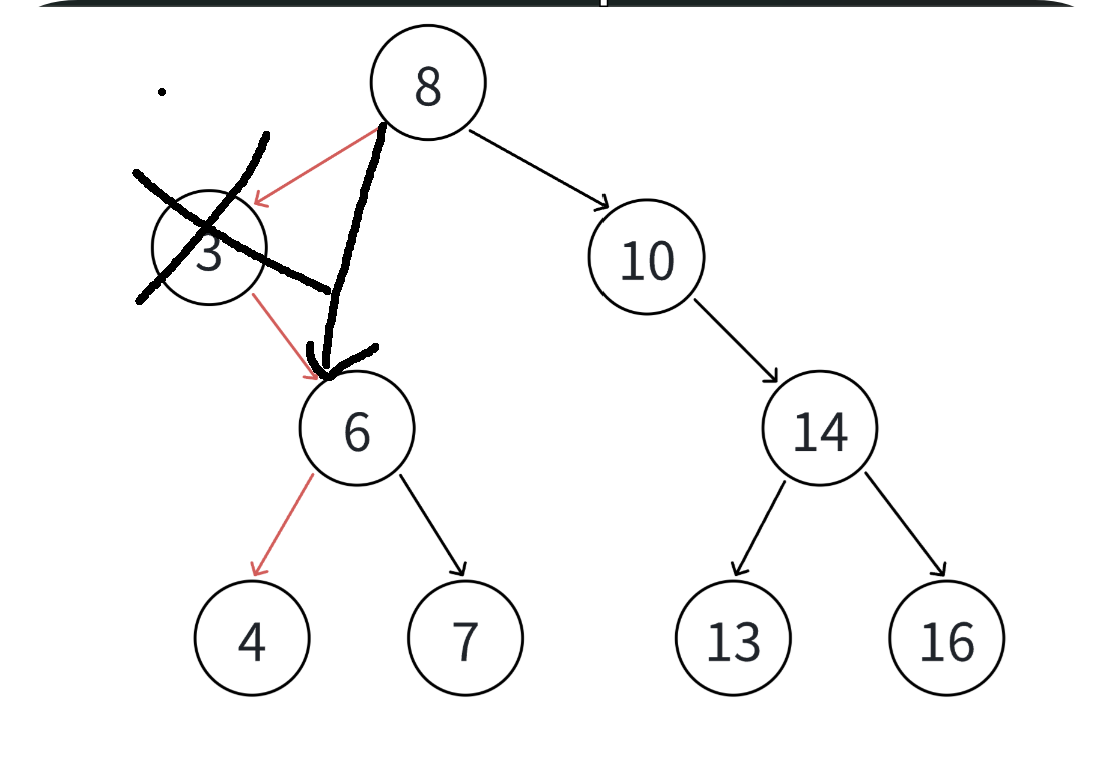
  1. 要删除的结点N右孩子位空，左孩子结点不为空，那么删除节点的父节点则应该指向删除节点的左孩子
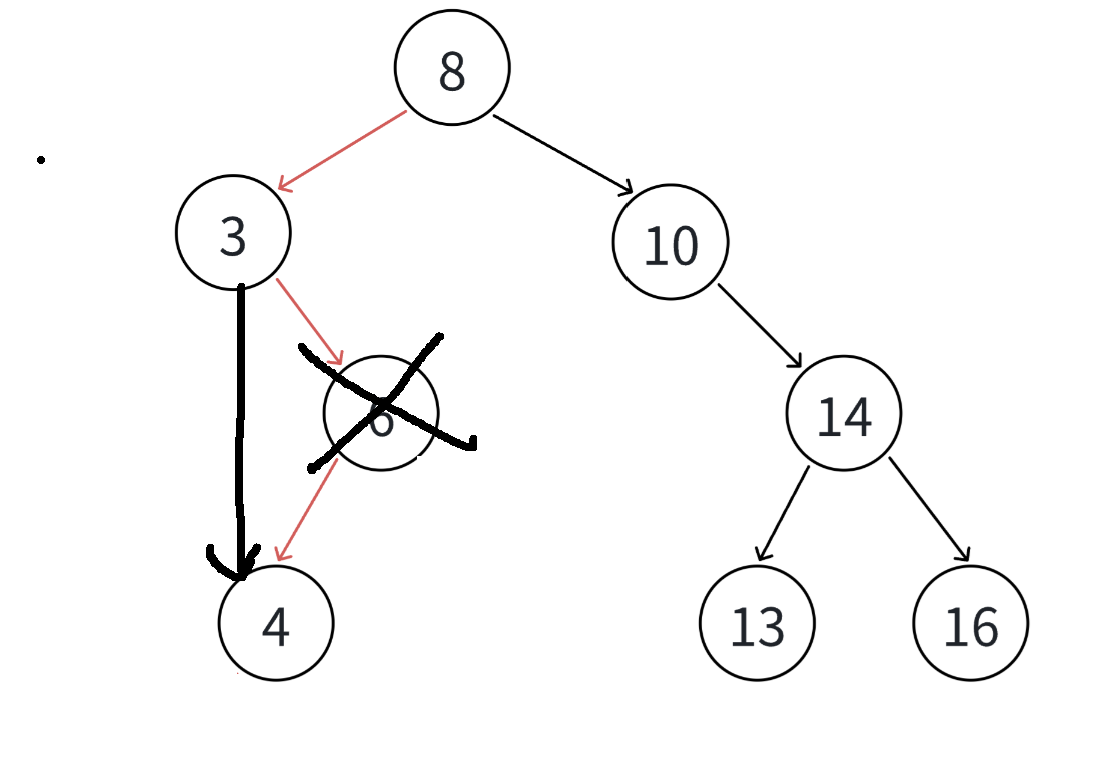
  1. 要删除的结点N左右孩子结点均不为空，那么这也是最复杂的情况

我们使用替代法

对于要删除的节点N

  1. 我们在N的左子树中找到最大的节点，然后把值替换给N，随后删除该节点

  2. 我们也可以在N的右子树中找到最小的节点，然后把值替换给N，随后删除该节点

上面两种方法任意一个都可以

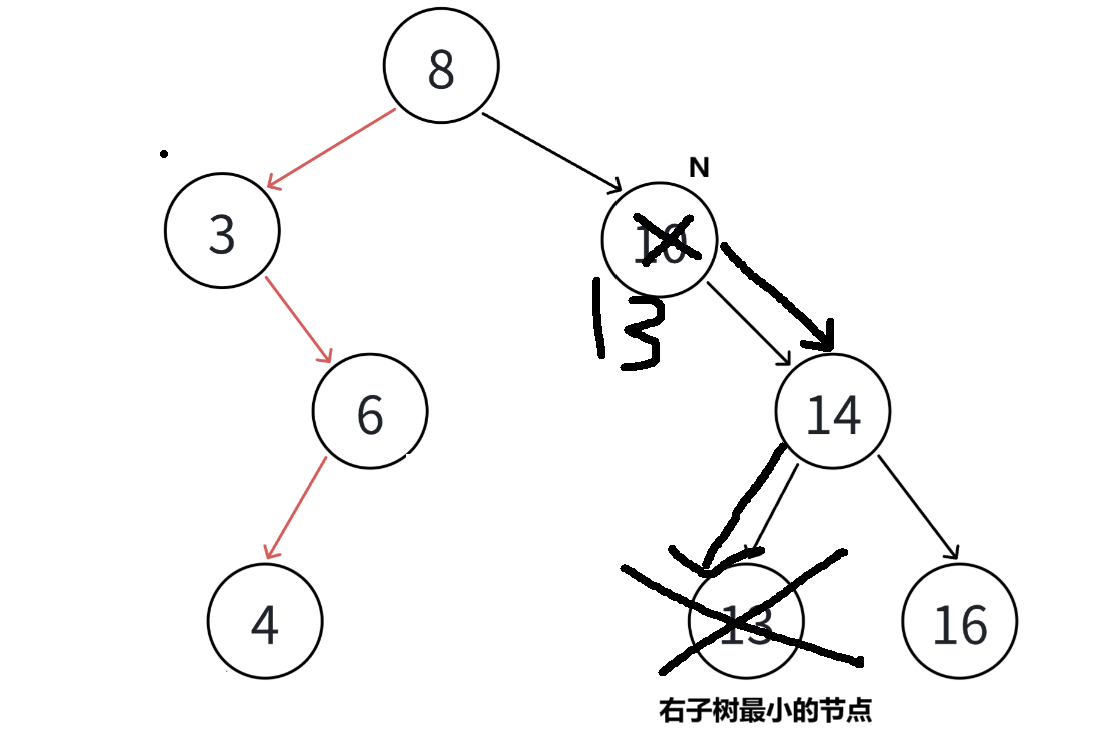
简单替换也不行，如果按这种方式找到了最小的节点，发现该节点还有右孩子，那么则要把其父节点指向右孩子

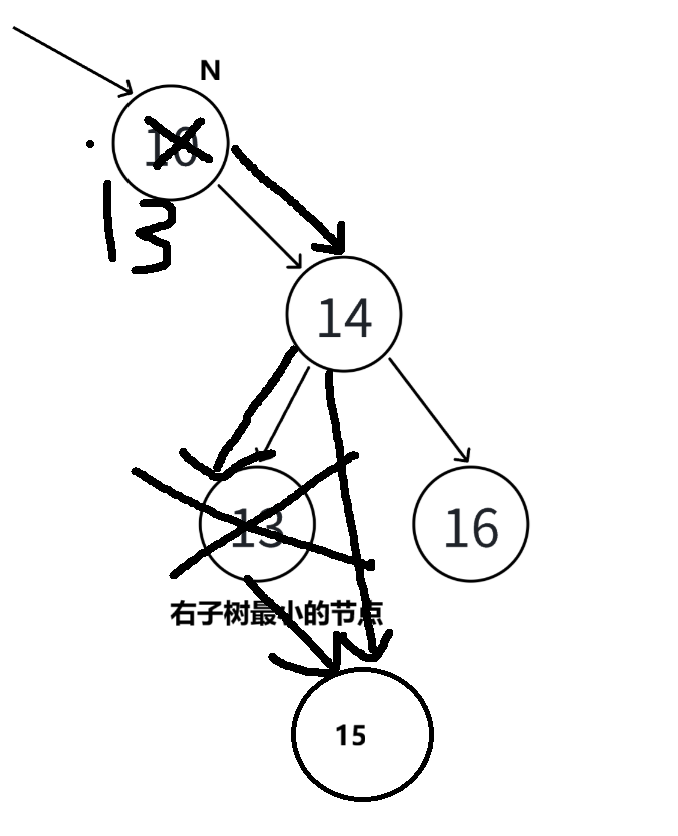
cpp 复制代码 
bool Erase(const K& key) {
    Node* parent = nullptr;
    Node* cur = _root;
    
    // 查找要删除的节点
    while (cur) {
        if (cur->_key < key) {
            parent = cur;
            cur = cur->_right;
        } else if (cur->_key > key) {
            parent = cur;
            cur = cur->_left;
        } else {
            // 找到要删除的节点，分情况处理
            if (cur->_left == nullptr) {
                // 情况1&2：左子树为空或左右子树均为空
                if (parent == nullptr) {
                    _root = cur->_right;
                } else {
                    if (parent->_left == cur) {
                        parent->_left = cur->_right;
                    } else {
                        parent->_right = cur->_right;
                    }
                }
                delete cur;
            } else if (cur->_right == nullptr) {
                // 情况3：右子树为空
                if (parent == nullptr) {
                    _root = cur->_left;
                } else {
                    if (parent->_left == cur) {
                        parent->_left = cur->_left;
                    } else {
                        parent->_right = cur->_left;
                    }
                }
                delete cur;
            } else {
                // 情况4：左右子树均不为空 - 替换法删除
                // 寻找右子树的最小节点
                Node* minParent = cur;
                Node* minRight = cur->_right;
                while (minRight->_left) {
                    minParent = minRight;
                    minRight = minRight->_left;
                }
                
                // 替换值
                cur->_key = minRight->_key;
                
                // 删除最小节点
                if (minParent->_left == minRight) {
                    minParent->_left = minRight->_right;
                } else {
                    minParent->_right = minRight->_right;
                }
                delete minRight;
            }
            return true;
        }
    }
    return false;  // 未找到要删除的节点
}

3.3.4 二叉搜索树的局限性

3.3.4.1 时间复杂度分析

| 操作 | 最佳情况 | 平均情况 | 最坏情况 |
| 查找 | O(log n) | O(log n) | O(n) |
| 插入 | O(log n) | O(log n) | O(n) |

删除 O(log n) O(log n) O(n)

说明：

  • 最佳情况：树完全平衡时

  • 最坏情况：树退化为链表时（输入有序数据）

3.3.4.2 局限性

普通二叉搜索树的主要问题：

  1. 性能不稳定：依赖于输入数据的顺序

  2. 可能退化为链表：当输入有序数据时

  3. 不平衡：不保证树的平衡性

3.4 AVL树

3.4.1 AVL树的概念

AVL树是最先发明的自平衡二叉查找树

其具有以下特性:

它的左右子树都是AVL树，且左右子树的高度差的绝对值不超过1。AVL树是一颗高度平衡搜索二叉树，通过控制高度差去控制平衡。

AVL树实现这里我们引入一个平衡因子(balance factor)的概念，每个结点都有一个平衡因子，任何结点的平衡因子等于右子树的高度减去左子树的高度，也就是说任何结点的平衡因子等于0/1/-1

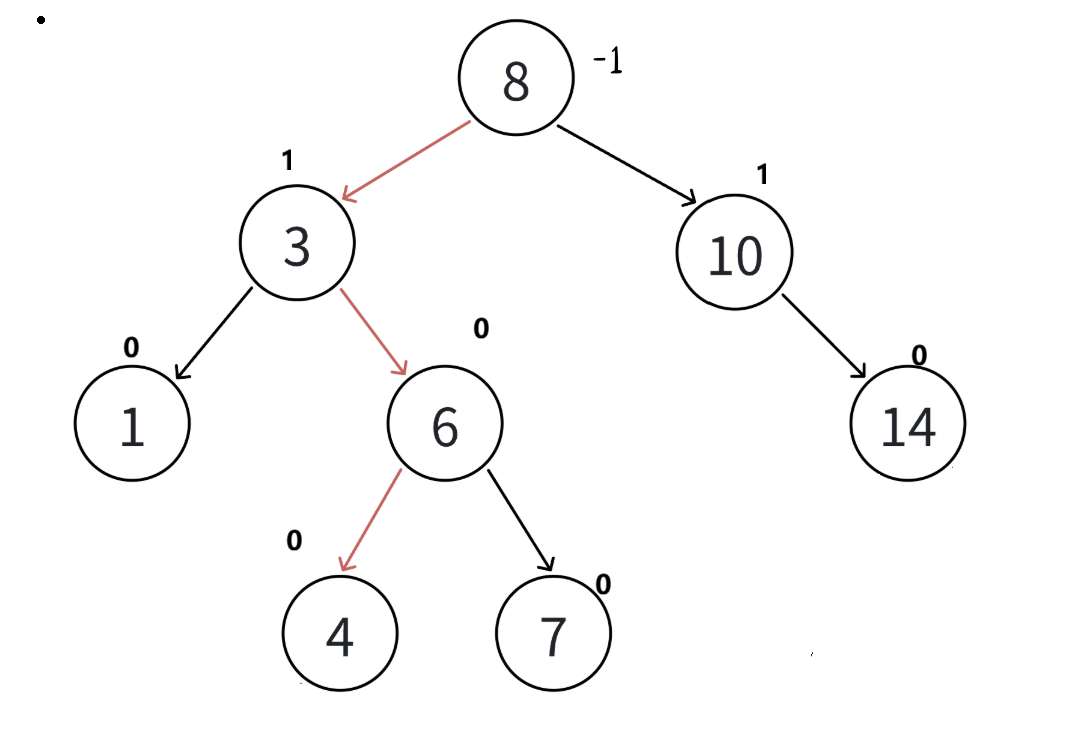
3.4.2 AVL树的构建

一般AVL树我们使用前面将的key/value组合，而在这里我们使用一个叫pair的类封装key和value(pair为库文件中的类)。这是一个专门处理两个值映射关系的类

cpp 复制代码 
template<class K, class V>
struct AVLTreeNode
{
    pair<K, V> _kv;
    AVLTreeNode<K, V>* _left;
    AVLTreeNode<K, V>* _right;
    AVLTreeNode<K, V>* _parent;
    int _bf; // balance factor

    AVLTreeNode(const pair<K, V>& kv)
        :_kv(kv)
        , _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _bf(0)
    {}
};
3.4.2.1 插入

插入过程我们先按照正常的搜索树规则实现

插入后必然会导致平衡因子的改变

  1. 如果是变为0,那么是从1或者-1变过去。根节点平衡因子也跟着改变，继续向上调整
  2. 如果是变为-1或者1，那么是从0变过去。高度没有变化，无需调整
  3. 如果是-2或者2，直接调整
cpp 复制代码 
bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    cur = new Node(kv);
    if (parent->_kv.first < kv.first)
    {
        parent->_right = cur;
    }
    else
    {
        parent->_left = cur;
    }
    cur->_parent = parent;

    // 更新平衡因子
    while (parent)
    {
        if (cur == parent->_left)
            parent->_bf--;
        else
            parent->_bf++;

        if (parent->_bf == 0)
        {
            break;
        }
        else if (parent->_bf == 1 || parent->_bf == -1)
        {
            cur = parent;
            parent = parent->_parent;
        }
        else if (parent->_bf == 2 || parent->_bf == -2)
        {
            // 不平衡了，旋转处理
            break;
        }
        else
        {
            assert(false);
        }
    }
    return true;
}
3.4.2.2 旋转

当平衡因子为-2或者2时，我们进行旋转操作

左单旋

当某个节点的右子树比左子树高2，且右子树的右子树比左子树高时，需要进行左单旋。

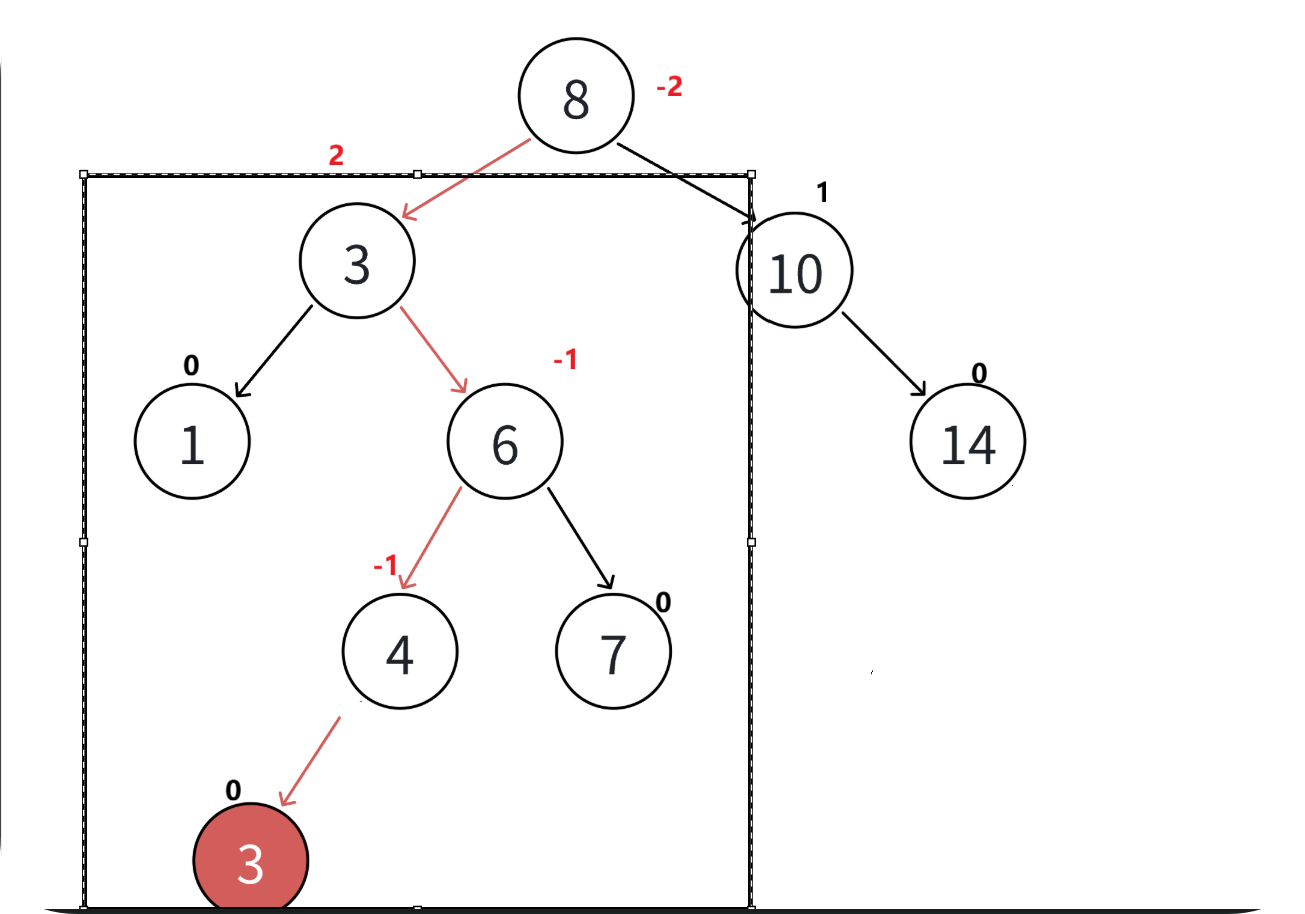
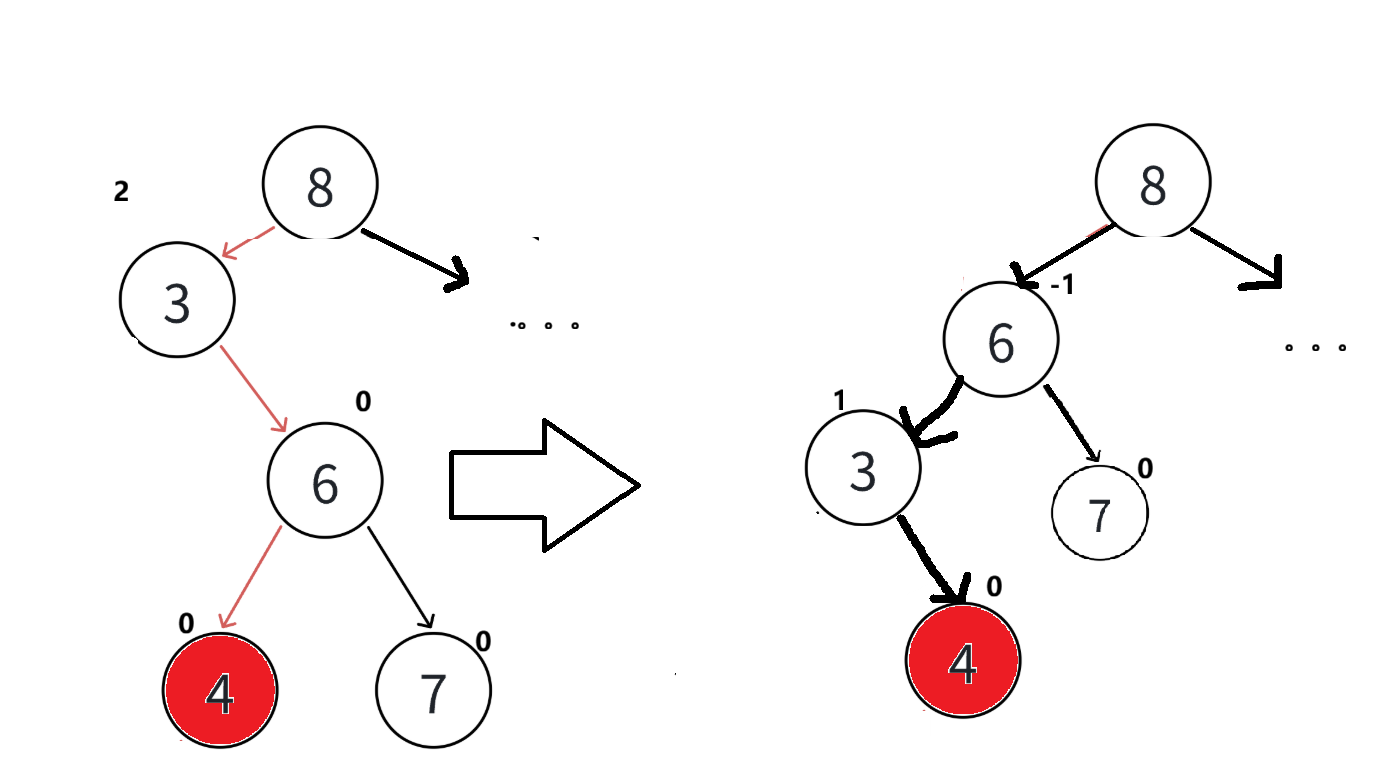
把3给压下去，换6上来，同时让3指向6的左孩子4。不要忘记让8之前指向的是3，现在要改为6

cpp 复制代码 
void RotateL(Node* parent)
{
    Node* subR = parent->_right;
    Node* subRL = subR->_left;

    parent->_right = subRL;
    if(subRL)
        subRL->_parent = parent;

    Node* parentParent = parent->_parent;

    subR->_left = parent;
    parent->_parent = subR;

    if (parentParent == nullptr)
    {
        _root = subR;
        subR->_parent = nullptr;
    }
    else
    {
        if (parent == parentParent->_left)
        {
            parentParent->_left = subR;
        }
        else
        {
            parentParent->_right = subR;
        }
        subR->_parent = parentParent;
    }
    parent->_bf = subR->_bf = 0;
}
右单旋

右单旋其实和左单旋十分相似，只是旋的方向相反而已

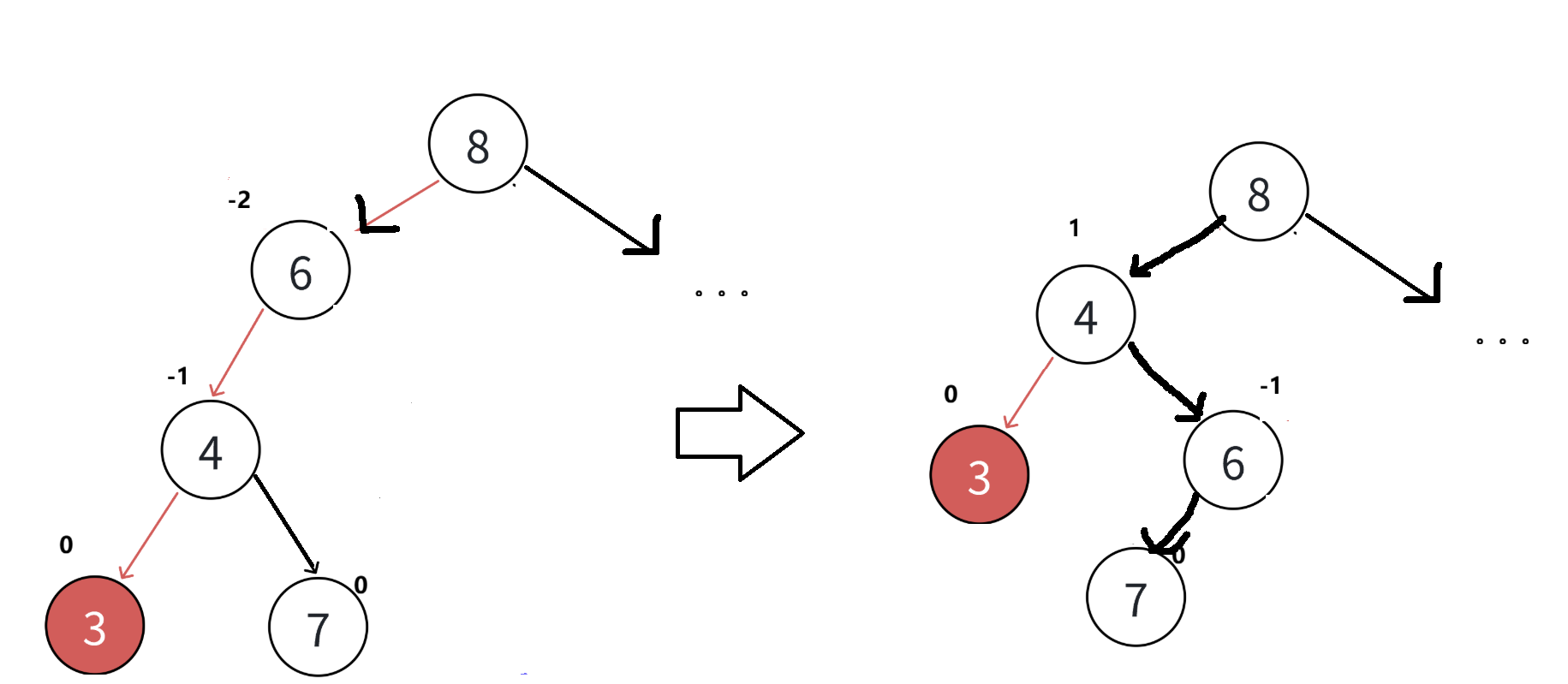
我们这次把6压下去，换4上来，然后6指向4的右孩子7，8指向4

cpp 复制代码 
void RotateR(Node* parent)
{
    Node* subL = parent->_left;
    Node* subLR = subL->_right;

    parent->_left = subLR;
    if (subLR)
        subLR->_parent = parent;

    Node* parentParent = parent->_parent;

    subL->_right = parent;
    parent->_parent = subL;

    if (parentParent == nullptr)
    {
        _root = subL;
        subL->_parent = nullptr;
    }
    else
    {
        if (parent == parentParent->_left)
        {
            parentParent->_left = subL;
        }
        else
        {
            parentParent->_right = subL;
        }
        subL->_parent = parentParent;
    }
    parent->_bf = subL->_bf = 0;
}
左右双旋

当不平衡的三个节点不在"一条直线"上时，进行双旋

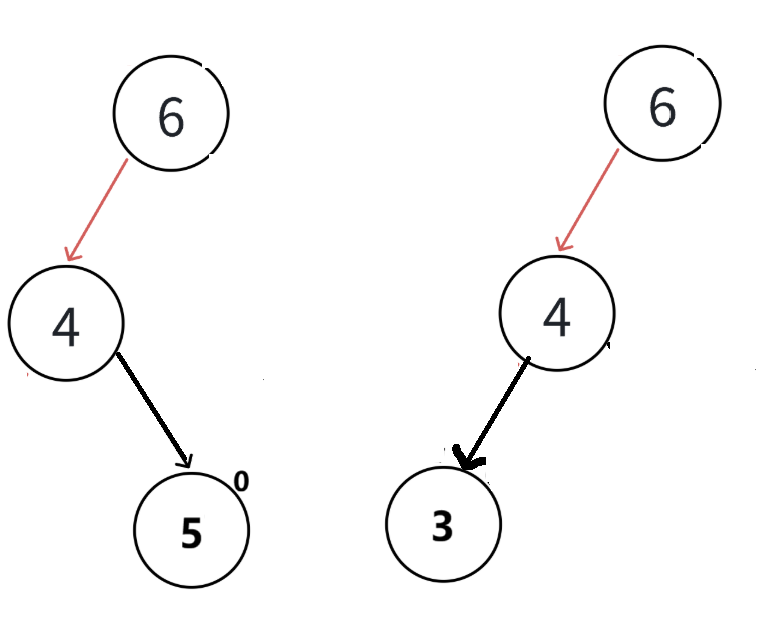
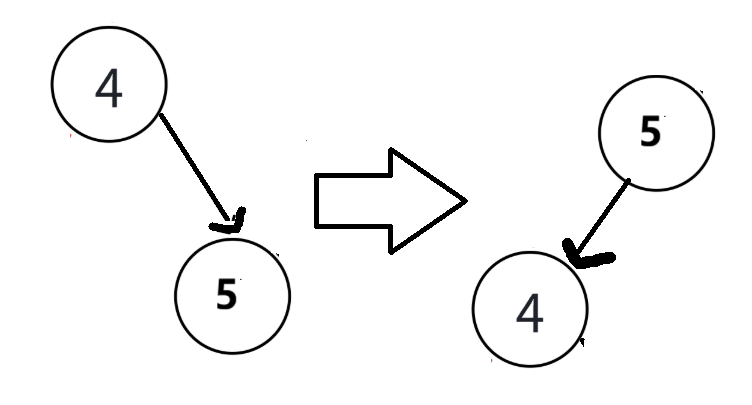
让4和5是往左下斜，而不是往右下斜，这样再次进行右旋即可

右左双旋

当某个节点的右子树比左子树高2，且右子树的左子树比右子树高时，需要进行右左双旋：先对右子树进行右旋，再对当前节点进行左旋。

与左右双旋的案例十分相似，我们不再做过多的讨论

3.5 红黑树

3.5.1 红黑树的概念

红黑树是一种特殊的二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色（红色或黑色）。通过对从根到叶子的任何路径上的节点颜色施加约束，红黑树确保没有任何一条路径会比其他路径长出两倍，因而保持了近似平衡的状态。

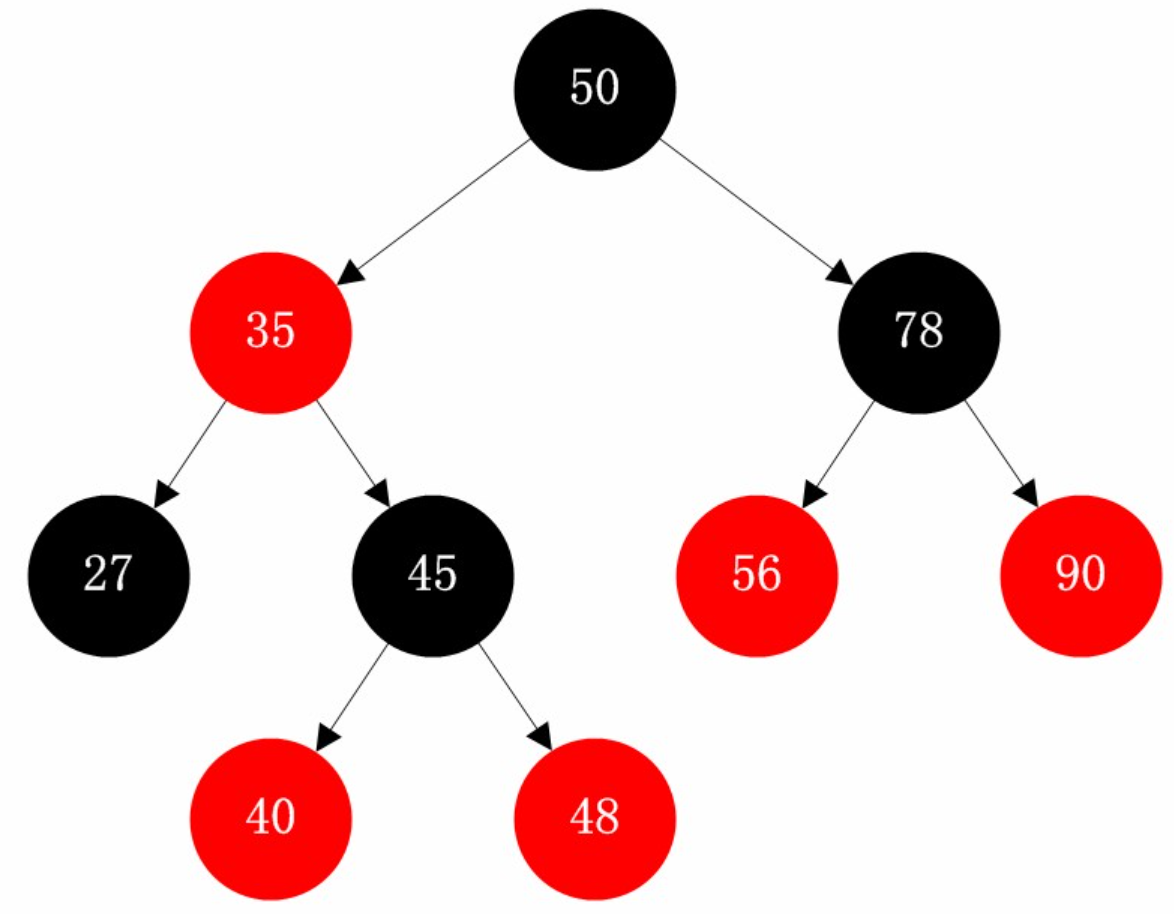
3.5.2 红黑树的规则

  1. 颜色规则：每个节点不是红色就是黑色

  2. 根节点规则：根节点必须是黑色的

  3. 红色节点规则 ：红色节点的两个子节点必须是黑色的（即不能有连续的红色节点）

  4. 黑色高度规则 ：从任意节点到其所有NULL 节点的简单路径上，包含相同数量的黑色节点

3.5.3 红黑树的构建

红黑树有红色和颜色，因此我们利用枚举常量

cpp 复制代码 
// 枚举值表示颜色
enum Colour {
    RED,
    BLACK
};

其余的与二叉搜索树相差无几

3.5.3.1 插入

红黑树的插入我们默认按照二叉搜索树的规则

如果是非空树 ，插入的一定是红色节点，因为红黑树保证每条路径上的黑色节点相同。如果插入黑色节点，那么会破坏相等这一条件

如果是空树，插入的节点作为根节点，颜色设为黑色

之后要检查并修复红黑树性质：如果父节点是黑色，插入完成；如果父节点是红色，需要根据叔叔节点的颜色进行不同的处理

3.5.3.2 变色

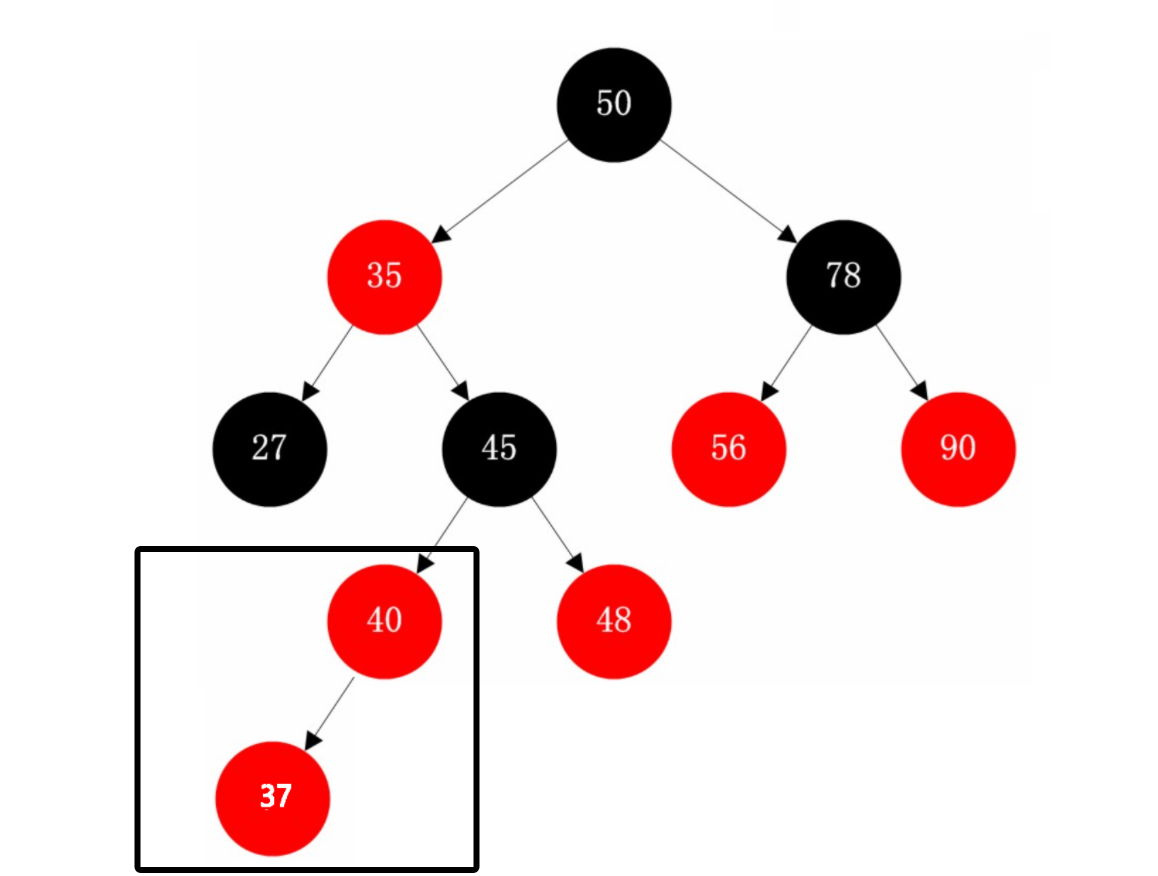
假设我们插入的节点之前是红色节点，那么就会出现红红的情况，因此我们需要进行变色处理

这里我们把新插入的节点37作为孩子，40作为父亲，45作为祖父，48作为叔叔

叔叔节点存在且为红色 (变色)

在这里叔叔存在且为红色，那么我们就把parent和uncle变为黑色，grandparent变为红色

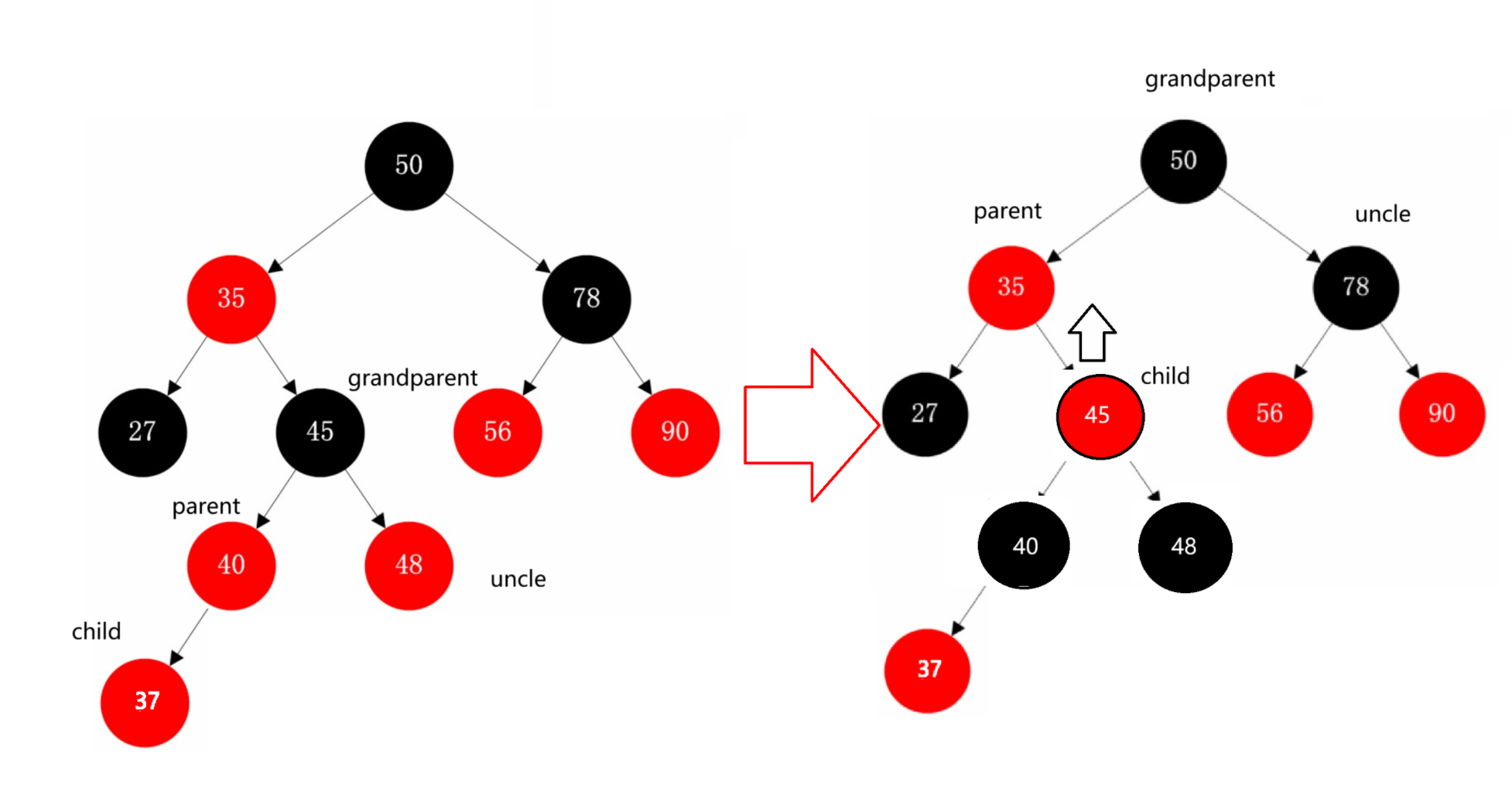
叔叔节点不存在或为黑色（旋转+变色）

单旋情况：

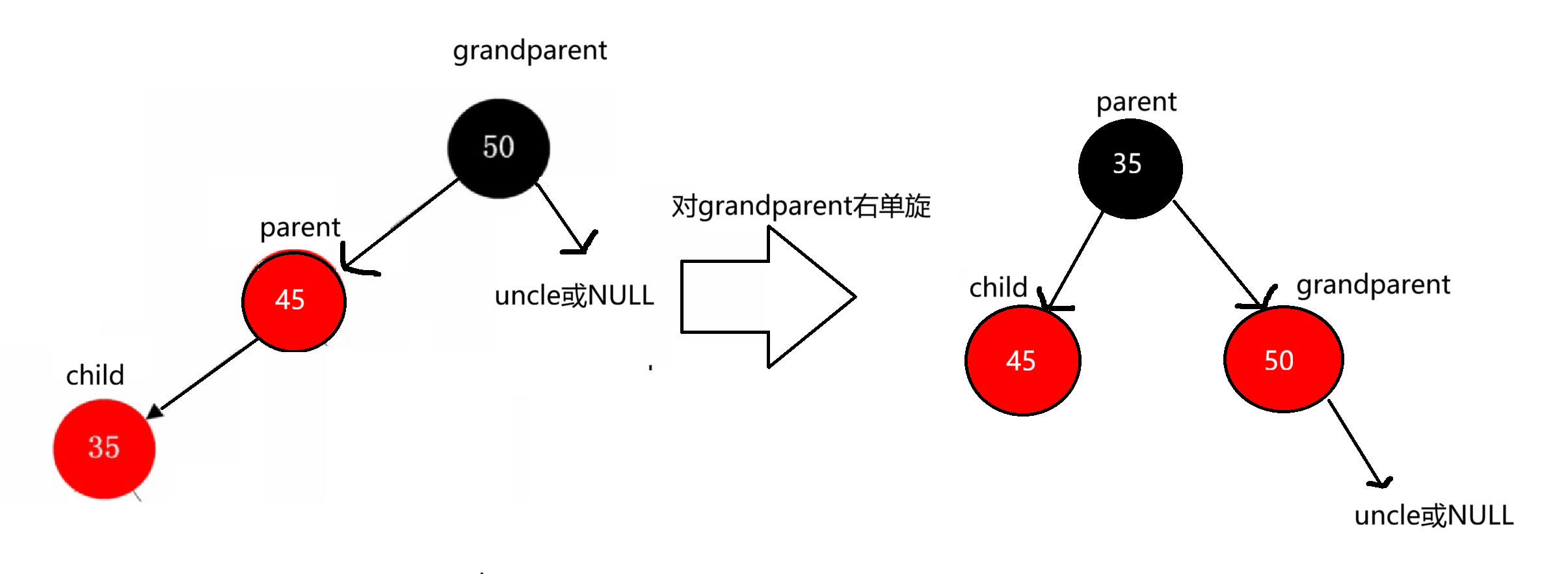
我们对grandparent进行右单旋，同时把parent变为黑色，grandparent变为黑色

双旋情况:

对于child在parent的右边情况，和AVL树类似，我们需要先对parent进行左单旋，保证三个节点在一条直线上，才能对grandparent进行右单旋

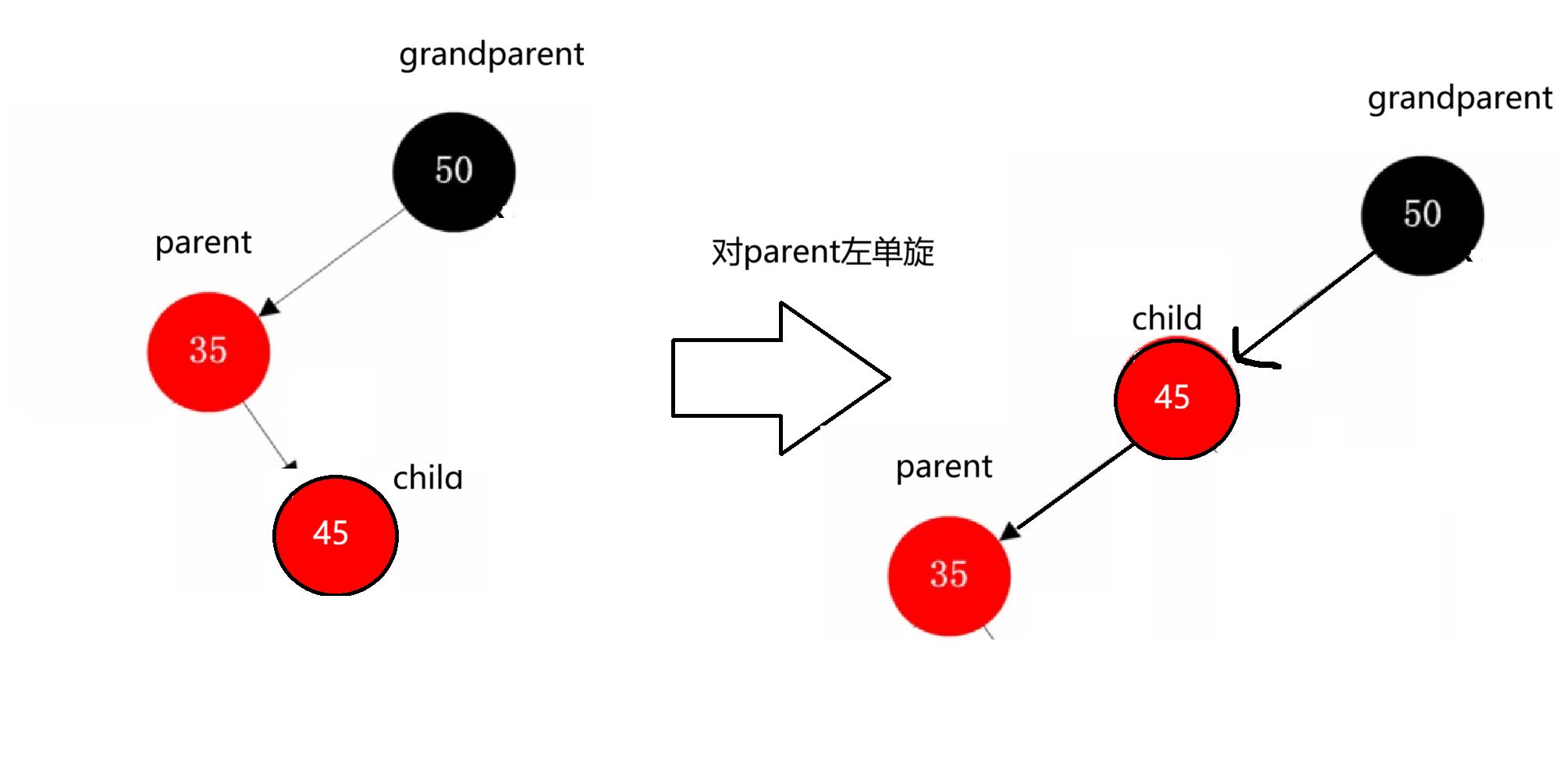
cpp 复制代码 
bool Insert(const K& key, const V& value)
{
	if (_root == nullptr)
	{
		_root = new Node({key,value});
		_root->_col = BLACK;
		return true;
	}
	Node* newnode = new Node({ key,value });
	newnode->_col = RED;
	Node* cur = _root;
	Node* child = cur;
	while (cur)//按照二叉搜索树的规则插入
	{
		if (key < cur->_kv.first)
		{
			child = cur;
			cur = cur->_left;
		}
		else if (key > cur->_kv.first)
		{
			child = cur;
			cur = cur->_right;
		}
		else
		{
			find(key)->_kv.second++;
			return true;
		}
	}
	if (key < child->_kv.first)
	{
		child->_left = newnode;
		newnode->_parent = child;
	}
	else
	{
		child->_right = newnode;
		newnode->_parent = child;
	}
	child = newnode;
	Node* parent = child->_parent;
	while (child->_col == RED && parent && parent->_col == RED)
//当child为红色时并且parent为黑色时继续循环
	{
		parent = child->_parent;
		Node* pparent = parent->_parent;
		Node* uncle = nullptr;
		if (pparent == nullptr)
			break;
		else
		{
			if (pparent->_left == parent)
				uncle = pparent->_right;
			else
				uncle = pparent->_left;

			if (uncle && uncle->_col == RED)//叔叔存在并且为红色直接变色
			{
				uncle->_col = BLACK;
				parent->_col = BLACK;
				pparent->_col = RED;
				child = pparent;
				parent = child->_parent;
			}
			else//叔叔不存在或者为黑色，需要旋转和变色
			{
				if (pparent->_left == parent)
				{
					if (parent->_right == child)
					{
						RotateL(parent);
						RotateR(pparent);
						child->_col = BLACK;
						pparent->_col = RED;
						
					}
					else
					{
						RotateR(pparent);
						parent->_col = BLACK;
						pparent->_col = RED;
						child = parent;
						parent = child->_parent;
					}
				}
				else
				{
					if (parent->_left == child)
					{
						RotateR(parent);
						RotateL(pparent);
						child->_col = BLACK;
						pparent->_col = RED;
					}
					else
					{
						RotateL(pparent);
						parent->_col = BLACK;
						pparent->_col = RED;
						child = parent;
						parent = child->_parent;
					}
				}
			}
		}
	}
	_root->_col = BLACK;//在变色处理时可能会对根节点进行变动，根节点需要保持黑色

	return true;
}

3.6 AVL树和红黑树的区别

3.6.1 基本性质差异

AVL树

  • 平衡定义：对于每个节点，左右子树高度差不超过1

  • 平衡因子 ：每个节点维护高度差 balance = height(left) - height(right) ∈ {-1, 0, 1}

  • 高度保证：树的高度严格为 O(log n)

  • 严格性：非常严格的平衡条件

红黑树

  • 五条性质：

    1. 每个节点是红色或黑色

    2. 根节点是黑色

    3. 所有叶子节点(NIL)是黑色

    4. 红色节点的子节点必须是黑色（不能有连续红色节点）

    5. 从任一节点到其每个叶子的所有路径包含相同数量的黑色节点

  • 高度保证：最长路径不超过最短路径的2倍，高度 ≤ 2log₂(n+1)

  • 宽松性：相对宽松的平衡条件

3.6.2 效率对比

3.6.2.1 时间复杂度
操作 AVL树 红黑树
查找 O(log n) O(log n)
插入 O(log n) O(log n)
删除 O(log n) O(log n)
3.6.2.2 实际性能差异

  • 查找密集型：AVL树更优（高度更低）

  • 插入/删除密集型：红黑树更优（旋转次数更少）

  • 内存占用：红黑树稍好（不需要存储高度）

3.6.3 核心区别对比

AVL树和红黑树都是十分优秀的二叉搜索树，我们合理选择即可

特性 AVL树 红黑树
平衡严格度 严格平衡 近似平衡
查找性能 更优 良好
插入性能 需要更多旋转 更优
删除性能 需要更多旋转 更优
旋转次数 O(1)次但可能更频繁 最多3次旋转
存储开销 需要存储高度/平衡因子 需要1位存储颜色
实现复杂度 相对简单 更复杂
适用场景 查找密集型应用 插入删除频繁的应用

3.6.4 实际应用中的选择

  • C++ STL : std::map, std::set 使用红黑树

  • Java : TreeMap, TreeSet 使用红黑树

  • 原因: 综合性能更好，适合通用目的

3.7 哈希

3.7.1 哈希概念

哈希（Hash）又称散列，是一种通过哈希函数建立关键字Key与存储位置映射关系的数据组织方式。其底层是vector

3.7.2 哈希冲突

在哈希表中，对于不同的key，我们进行整型转换，哈希函数转换成下标时仍然相等，那么就造成了哈希冲突

3.7.3 哈希函数

哈希函数是我们设计出来来尽量避免哈希冲突的方式，是用来对key的加工处理，然后作下标

3.7.3.1 除法散列法/除留余数法

假设哈希表的大小为M，那么通过key除以M的余数作为 映射位置的下标，也就是哈希函数为：h(key)=key%M。

使用除法散列法时，要尽量避免M为某些值，如2的幂，10的幂等

3.7.3.2 乘法散列法

用关键字K乘上常数A(0<A<1)，并抽 取出k*A的小数部分。第二步：后再用M乘以k*A的小数部分，再向下取整。其中我们一般使用常数A为黄金分割比例，即0.6180339887

假设M为1024，key为1234，A=0.6180339887,A*key = 762.6539420558，取小数部分为0.6539420558, M×((A×key)%1.0)=0.6539420558*1024= 669.6366651392，那么h(1234)=669。

3.7.4 处理哈希冲突

我们所用的哈希函数只能够尽量避免哈希冲突，但无法完全处理。还是碰到哈希冲突时，我们就得想办法处理

3.7.4.1 开放定址法

在开放定址法中所有的元素都放到哈希表里，当⼀个关键字key用哈希函数计算出的位置冲突了，则按照某种规则找到一个没有存储数据的位置进行存储

线性探测

从发生冲突的位置开始，依次线性向后 探测，直到寻找到下⼀个没有存储数据的位置为止，如果走到哈希表尾，则回绕到哈希表头的位置。

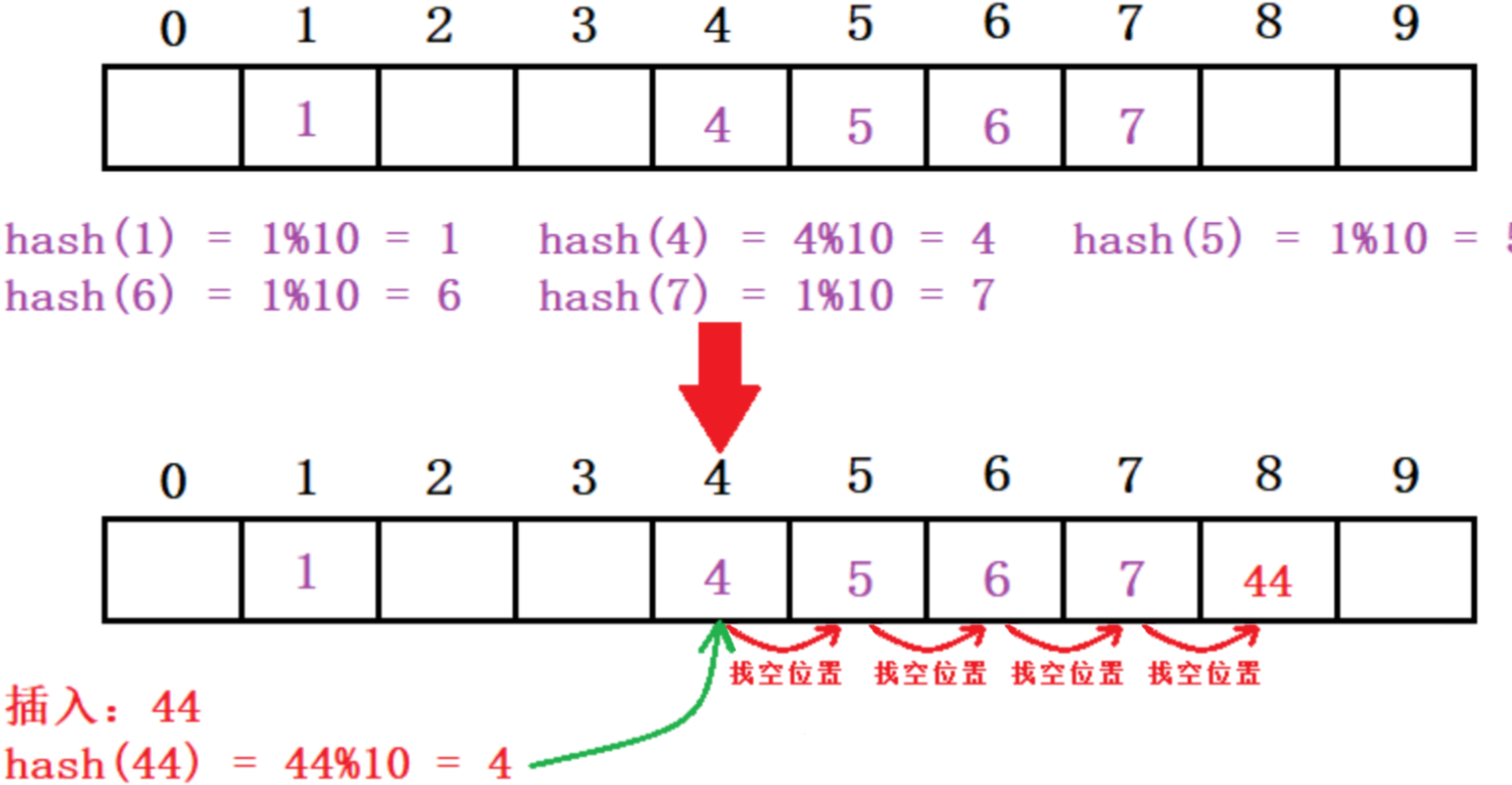
二次探测

从发生冲突的位置开始，依次左右按二次方跳跃式探测，直到寻找到下⼀个没有存储数据的位置为 止，如果往右走到哈希表尾，则回绕到哈希表头的位置；如果往左走到哈希表头，则回绕到哈希表 尾的位置；

开放定址法代码实现
cpp 复制代码 
namespace open_address {
    enum State {
        EXIST,
        EMPTY, 
        DELETE
    };
    
    template<class K, class V>
    struct HashData {
        pair<K, V> _kv;
        State _state = EMPTY;
    };
    
    template<class K, class V, class Hash = HashFunc<K>>
    class HashTable {
    private:
        vector<HashData<K, V>> _tables;
        size_t _n = 0;  // 元素个数
        
    public:
        bool Insert(const pair<K, V>& kv) {
            if (Find(kv.first)) return false;
            
            // 负载因子 > 0.7 时扩容
            if (_n * 10 / _tables.size() >= 7) {
                // 扩容逻辑...
            }
            
            Hash hash;
            size_t hashi = hash(kv.first) % _tables.size();
            size_t i = 1;
            
            // 线性探测寻找空位置
            while (_tables[hashi]._state == EXIST) {
                hashi = (hashi + i) % _tables.size();
                ++i;
            }
            
            _tables[hashi]._kv = kv;
            _tables[hashi]._state = EXIST;
            ++_n;
            return true;
        }
        
        HashData<K, V>* Find(const K& key) {
            Hash hash;
            size_t hashi = hash(key) % _tables.size();
            size_t i = 1;
            
            while (_tables[hashi]._state != EMPTY) {
                if (_tables[hashi]._state == EXIST && 
                    _tables[hashi]._kv.first == key) {
                    return &_tables[hashi];
                }
                hashi = (hashi + i) % _tables.size();
                ++i;
            }
            return nullptr;
        }
    };
}
3.7.4.2 链地址法(哈希桶)

链地址法相当于是vector中的每个元素都变成了链表，冲突的元素利用链表连接即可，因此也被形象地称为哈希桶

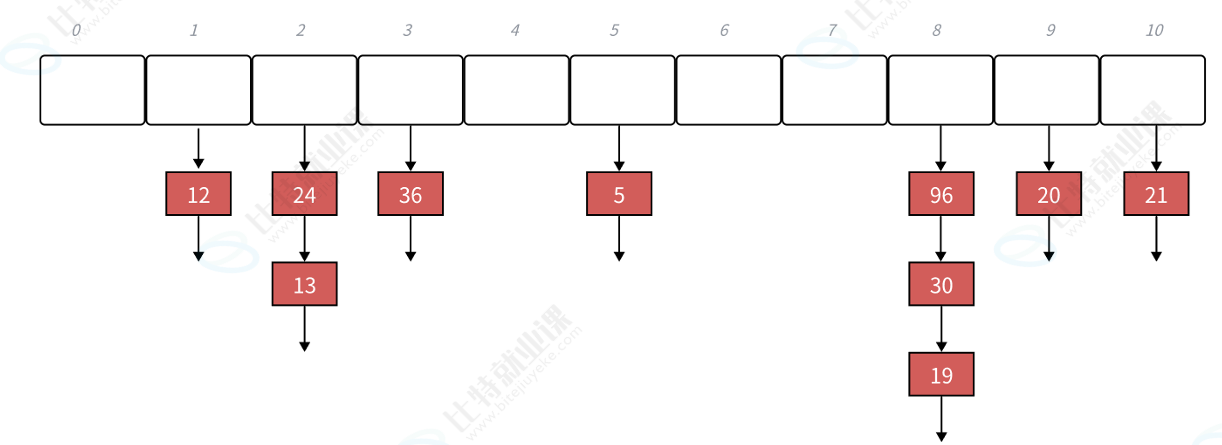
链地址法代码实现
cpp 复制代码 
namespace hash_bucket {
    template<class T>
    struct HashNode {
        T _data;
        HashNode<T>* _next;
        
        HashNode(const T& data)
            : _data(data)
            , _next(nullptr)
        {}
    };
    
    template<class K, class T, class KeyOfT, class Hash>
    class HashTable {
    private:
        vector<HashNode<T>*> _tables;
        size_t _n = 0;
        
    public:
        bool Insert(const T& data) {
            KeyOfT kot;
            if (Find(kot(data))) return false;
            
            // 负载因子 = 1 时扩容
            if (_n == _tables.size()) {
                vector<HashNode<T>*> new_tables(GetNextPrime(_tables.size()), nullptr);
                // 重新哈希所有元素...
                _tables.swap(new_tables);
            }
            
            Hash hs;
            size_t hashi = hs(kot(data)) % _tables.size();
            
            // 头插法
            HashNode<T>* new_node = new HashNode<T>(data);
            new_node->_next = _tables[hashi];
            _tables[hashi] = new_node;
            ++_n;
            
            return true;
        }
        
        // 其他方法...
    };
}
极端情况下的哈希桶改良

哈希桶能大幅改善哈希冲突，但若仍然冲突得很厉害

使得一个桶下挂了好几个节点，那么就得改良

例如我们可以把哈希桶-链表改为红黑树

或者使用布隆过滤器过滤没必要的节点

3.7.5 效率分析

3.7.5.1 时间复杂度分析
操作 平均情况 最坏情况 备注
插入 O(1) O(n) 最坏情况发生在所有键哈希冲突时
查找 O(1) O(n) 同上
删除 O(1) O(n) 同上
遍历 O(n) O(n) 需要访问所有元素
3.7.5.2 空间复杂度分析

  • 平均情况: O(n)

  • 实际开销: 通常比数组多 20-50% 的空间

  • 影响因素: 负载因子、冲突解决策略、哈希函数质量

3.8 位图

3.8.1 位图的概念

位图是一种使用比特位（bit）来表示数据的高效数据结构。每个比特位只能表示0或1，通常用来表示某个元素是否存在。

核心思想

  • 用1个比特表示1个元素的状态

  • 极大节省存储空间（相比使用字节或整数）

  • 支持高效的位运算操作

3.8.2 位图的实现

cpp 复制代码 
#include <vector>
#include <iostream>
#include <bitset>

class Bitmap {
private:
    std::vector<uint32_t> data;  // 使用32位整数数组存储位
    size_t size;                 // 位图总大小（比特数）
    
public:
    // 构造函数
    Bitmap(size_t num_bits) : size(num_bits) {
        // 计算需要多少个32位整数
        size_t array_size = (num_bits + 31) / 32;
        data.resize(array_size, 0);
    }
    
    // 设置某位为1
    void set(size_t pos) {
        if (pos >= size) return;
        
        size_t index = pos / 32;      // 在哪个整数中
        size_t offset = pos % 32;     // 在整数中的哪一位
        
        data[index] |= (1U << offset);
    }
    
    // 设置某位为0
    void reset(size_t pos) {
        if (pos >= size) return;
        
        size_t index = pos / 32;
        size_t offset = pos % 32;
        
        data[index] &= ~(1U << offset);
    }
    
    // 测试某位是否为1
    bool test(size_t pos) const {
        if (pos >= size) return false;
        
        size_t index = pos / 32;
        size_t offset = pos % 32;
        
        return (data[index] >> offset) & 1;
    }
    
    // 获取位图大小
    size_t getSize() const {
        return size;
    }
    
    // 统计1的个数（Population Count）
    size_t count() const {
        size_t cnt = 0;
        for (uint32_t val : data) {
            // 使用内置函数或手动计算
            cnt += __builtin_popcount(val);
        }
        return cnt;
    }
    
};

3.8.3 位图的实际用处

位图可用于海量数据的查找

假设有10亿个整型，现在要你统计不存在的数字

我们当然不能使用红黑树和哈希表，因为10亿个元素放在树和哈希中根本放不下

我们就可以使用简化版的哈希:位图，每个节点就用一个二进制位来表示存不存在

10亿个比特位也就125mb左右而已

3.9 布隆过滤器

3.9.1 布隆过滤器的概念

布隆过滤器是一种空间效率高 的概率型数据结构，用于快速判断一个元素是否不在集合中 。它可能会产生假阳性 （False Positive），但不会产生假阴性（False Negative）。

核心特性

  • ✅ 空间效率极高：相比哈希表节省大量内存

  • ✅ 查询速度极快：O(k) 时间复杂度（k为哈希函数个数）

  • ✅ 不会漏报：如果布隆过滤器说元素不存在，那一定不存在

  • ❌ 可能误报：如果布隆过滤器说元素存在，实际上可能不存在

  • ❌ 不支持删除：标准布隆过滤器不支持删除操作

3.9.2 布隆过滤器原理

cpp 复制代码 
添加元素 "apple":
1. 计算 k 个哈希值: h1("apple"), h2("apple"), h3("apple")
2. 将位数组中对应位置设为1: bits[h1], bits[h2], bits[h3]

查询元素 "apple":
1. 计算 k 个哈希值
2. 检查所有对应位是否都为1
   - 如果都是1 → "可能存在"
   - 如果有任一位是0 → "肯定不存在"

这就相当于是判断几个二进制位

3.9.3 基础实现

cpp 复制代码 
#include <vector>
#include <functional>
#include <bitset>
#include <iostream>
#include <string>

class SimpleBloomFilter {
private:
    std::vector<bool> bits;  // 位数组
    size_t size;             // 位数组大小
    int num_hash_functions;  // 哈希函数个数
    
    // 生成哈希值
    size_t hash(const std::string& element, int seed) const {
        std::hash<std::string> hasher;
        return (hasher(element) + seed * 0x9e3779b9) % size;
    }
    
public:
    SimpleBloomFilter(size_t bit_size, int hash_count) 
        : size(bit_size), num_hash_functions(hash_count) {
        bits.resize(size, false);
    }
    
    // 添加元素
    void add(const std::string& element) {
        for (int i = 0; i < num_hash_functions; i++) {
            size_t index = hash(element, i);
            bits[index] = true;
        }
    }
    
    // 检查元素是否存在（可能有误报）
    bool mightContain(const std::string& element) const {
        for (int i = 0; i < num_hash_functions; i++) {
            size_t index = hash(element, i);
            if (!bits[index]) {
                return false; // 肯定不存在
            }
        }
        return true; // 可能存在
    }
    
    // 获取位数组使用率
    double getUsageRatio() const {
        size_t used_bits = 0;
        for (bool bit : bits) {
            if (bit) used_bits++;
        }
        return static_cast<double>(used_bits) / size;
    }
    
    // 打印统计信息
    void printStats() const {
        std::cout << "布隆过滤器统计:" << std::endl;
        std::cout << "位数组大小: " << size << std::endl;
        std::cout << "哈希函数个数: " << num_hash_functions << std::endl;
        std::cout << "位数组使用率: " << getUsageRatio() * 100 << "%" << std::endl;
    }
};

4. 排序算法

排序：所谓排序，就是使⼀串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的 操作。

4.1 插入排序

直接插入排序

直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值的大小逐个插入到⼀个已经排好序的有序序列中，直到所有的记录插入完为止，得到⼀个新的有序序列。

过程演示（以数组[5,3,9,6,2]为例）：

初始: [5, 3, 9, 6, 2]

第1轮: [3, 5, 9, 6, 2] // 插入3

第2轮: [3, 5, 9, 6, 2] // 插入9

第3轮: [3, 5, 6, 9, 2] // 插入6

第4轮: [2, 3, 5, 6, 9] // 插入2

cpp 复制代码 
void InsertSort(int* a, int n) {
    for (int i = 0; i < n - 1; i++) {
        int end = i;
        int tmp = a[end + 1];
        
        // 从后往前比较并移动元素
        while (end >= 0) {
            if (a[end] > tmp) {
                a[end + 1] = a[end];
                end--;
            } else {
                break;
            }
        }
        a[end + 1] = tmp;
    }
}

特性总结：

  • 时间复杂度：O(N²)

  • 空间复杂度：O(1)

  • 稳定性：稳定

  • 适用场景：数据量小或基本有序的情况

希尔排序

希尔排序的底层仍为插入排序，但正式排序前有预排序这一过程

先选定一个整数（通常是gap=n/3+1），把待排序文件所有记录分成各组，所有的距离相等的记录分在同一组内，并对每一组内的记录进行排序,然后gap=gap/3+1，继续排序

省流:相隔gap个距离的数据相互进行排序，最后gap=1时就为正常的插入排序

cpp 复制代码 
void ShellSort(int* a, int n) {
    int gap = n;
    while (gap > 1) {
        gap = gap / 3 + 1;  // 常用的增量序列
        
        for (int i = 0; i < n - gap; i++) {
            int end = i;
            int tmp = a[end + gap];
            
            while (end >= 0) {
                if (a[end] > tmp) {
                    a[end + gap] = a[end];
                    end -= gap;
                } else {
                    break;
                }
            }
            a[end + gap] = tmp;
        }
    }
}

特性总结：

  • 时间复杂度：O(N¹·³) ~ O(N²)

  • 空间复杂度：O(1)

  • 稳定性：不稳定

  • 优势：对直接插入排序的优化，中等规模数据表现良好

4.2 选择排序

直接选择排序

选择排序的基本思想： 每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

cpp 复制代码 
void SelectSort(int* a, int n) {
    int begin = 0, end = n - 1;
    
    while (begin < end) {
        int mini = begin, maxi = begin;
        
        // 找出最小和最大元素的下标
        for (int i = begin; i <= end; i++) {
            if (a[i] > a[maxi]) maxi = i;
            if (a[i] < a[mini]) mini = i;
        }
        
        // 处理边界情况
        if (begin == maxi) maxi = mini;
        
        // 交换元素
        Swap(&a[mini], &a[begin]);
        Swap(&a[maxi], &a[end]);
        
        begin++;
        end--;
    }
}

void Swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

特性总结：

  • 时间复杂度：O(N²)

  • 空间复杂度：O(1)

  • 稳定性：不稳定

  • 特点：思路简单但效率低

堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法

升序要大堆，排降序建小堆

cpp 复制代码 
// 向下调整算法
void AdjustDown(int* a, int n, int parent) {
    int child = parent * 2 + 1;
    
    while (child < n) {
        // 选出较大的孩子
        if (child + 1 < n && a[child + 1] > a[child]) {
            child++;
        }
        
        // 如果孩子大于父亲，需要调整
        if (a[child] > a[parent]) {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        } else {
            break;
        }
    }
}

void HeapSort(int* a, int n) {
    // 建堆：从最后一个非叶子节点开始调整
    for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
        AdjustDown(a, n, i);
    }
    
    // 排序：将堆顶元素与末尾交换，然后调整堆
    int end = n - 1;
    while (end > 0) {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        end--;
    }
}

特性总结：

  • 时间复杂度：O(NlogN)

  • 空间复杂度：O(1)

  • 稳定性：不稳定

  • 优势：时间复杂度稳定，适合大数据量排序

4.3 交换排序

冒泡排序

通过相邻元素的比较和交换，使较大的元素逐渐移动到序列末尾。

cpp 复制代码 
void BubbleSort(int* a, int n) {
    int exchange = 0;
    
    for (int i = 0; i < n; i++) {
        exchange = 0;
        
        for (int j = 0; j < n - i - 1; j++) {
            if (a[j] > a[j + 1]) {
                Swap(&a[j], &a[j + 1]);
                exchange = 1;
            }
        }
        
        // 如果没有发生交换，说明已经有序
        if (exchange == 0) break;
    }
}

特性总结：

  • 时间复杂度：O(N²)

  • 空间复杂度：O(1)

  • 稳定性：稳定

  • 特点：实现简单，但效率较低

快速排序

核心思想: 递归

我们先选择最左边的值为key值，创造两个指针，一个从左往右 找比key大 的值，一个从右往左 找比key小的值，随后交换，继续找。知道两个指针碰面时停下，将停下位置的数据与key值的数据交换。随后对key左边和右边的区间进行相同的操作。

如果是选取最左边的为key值，那么一定要先让右边的指针先动

cpp 复制代码 
// 快速排序主函数
void QuickSort(int* a, int left, int right) {
    if (left >= right) return;
    
    int keyi = PartSort1(a, left, right);  // 分割
    QuickSort(a, left, keyi - 1);          // 递归左半部分
    QuickSort(a, keyi + 1, right);         // 递归右半部分
}

// hoare分割法
int PartSort1(int* a, int left, int right) {
    int keyi = left;
    
    while (left < right) {
        // 右边找小于基准的值
        while (left < right && a[right] >= a[keyi]) {
            right--;
        }
        // 左边找大于基准的值
        while (left < right && a[left] <= a[keyi]) {
            left++;
        }
        Swap(&a[left], &a[right]);
    }
    Swap(&a[keyi], &a[left]);
    return left;
}

非递归快速排序

非递归版本的快速排序需要借助数据结构：栈

递归一个作用就是确定再次排序的区间的范围，所以我们传递left和right

那我们提前将区间的范围压入栈，到时候再取出即可

cpp 复制代码 
// 需要栈的支持
void QuickSortNonR(int* a, int left, int right) {
    // 使用栈模拟递归过程
    int stack[1000];
    int top = -1;
    
    stack[++top] = left;
    stack[++top] = right;
    
    while (top >= 0) {
        right = stack[top--];
        left = stack[top--];
        
        int keyi = PartSort3(a, left, right);
        
        // 左半部分入栈
        if (left < keyi - 1) {
            stack[++top] = left;
            stack[++top] = keyi - 1;
        }
        // 右半部分入栈
        if (keyi + 1 < right) {
            stack[++top] = keyi + 1;
            stack[++top] = right;
        }
    }
}

快速排序特性总结：

  • 平均时间复杂度：O(NlogN)

  • 最坏时间复杂度：O(N²)（当数据已经有序时）

  • 空间复杂度：O(logN) ~ O(N)

  • 稳定性：不稳定

  • 优势：在实践中通常是最快的排序算法

4.4 归并排序

递归版

基本思想：采用分治策略，先将序列递归分解，再将有序子序列合并。

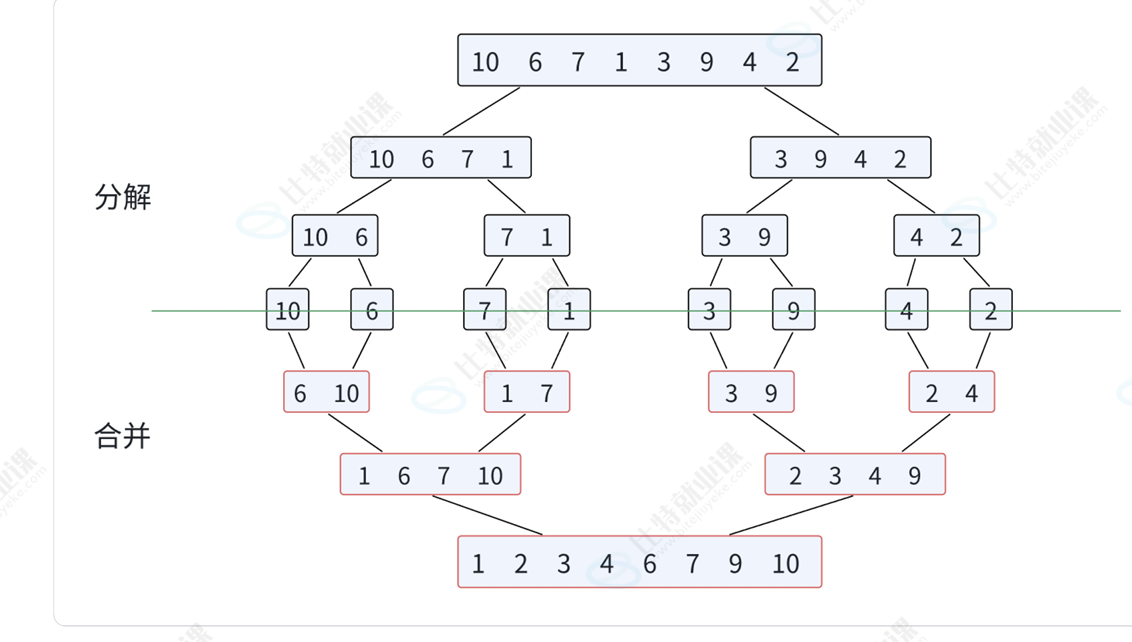
我们利用递归拆分为一个个小区间(最小的只有一个值)，再把相邻的两个小区间的值合并在一起形成一个更大的有序的序列，然后再合并，再合并直到完全

cpp 复制代码 
void _MergeSort(int* a, int left, int right, int* tmp) {
    if (left >= right) return;
    
    int mid = (left + right) / 2;
    
    // 递归分解
    _MergeSort(a, left, mid, tmp);
    _MergeSort(a, mid + 1, right, tmp);
    
    // 合并两个有序序列
    int begin1 = left, end1 = mid;
    int begin2 = mid + 1, end2 = right;
    int index = left;
    
    while (begin1 <= end1 && begin2 <= end2) {
        if (a[begin1] < a[begin2]) {
            tmp[index++] = a[begin1++];
        } else {
            tmp[index++] = a[begin2++];
        }
    }
    
    // 处理剩余元素
    while (begin1 <= end1) tmp[index++] = a[begin1++];
    while (begin2 <= end2) tmp[index++] = a[begin2++];
    
    // 拷贝回原数组
    for (int i = left; i <= right; i++) {
        a[i] = tmp[i];
    }
}

void MergeSort(int* a, int n) {
    int* tmp = (int*)malloc(sizeof(int) * n);
    _MergeSort(a, 0, n - 1, tmp);
    free(tmp);
}

非递归版

我们先把整个数组中的每个数据分为一个小区间(一个数就是最小的一个区间)，随后两个数进行合并，2个数再和2个数合并，4个和4个合并，直到完全

如果在数组末尾，出现合并个数不够，例如4个和2个合并，也照样进行

cpp 复制代码 
void MergeSortNonR(int* arr, int len)
{
	int* tmp = malloc(sizeof(int) * len);
	int gap = 1;//先把1个数当作一个小区间
	while (gap < len)
	{
		for (int j = 0; j < len - gap; j += 2*gap)
		{
			int begin1 = j;//第一个小区间的开头
			int end1 = j + gap-1;。。第一个小区间的末尾
			int begin2 = end1 + 1;//第二个小区间的开头
			int end2 = (begin2 + gap > len) ? len - 1:begin2 + gap-1;//第二个小区间的末尾
			int i = j;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (arr[begin1] < arr[begin2])
				{
					tmp[i] = arr[begin1];
					begin1++;
				}
				else
				{
					tmp[i] = arr[begin2];
					begin2++;
				}
				i++;
			}
			while (begin1 <= end1)
			{
				tmp[i] = arr[begin1];
				begin1++;
				i++;
			}
			while (begin2 <= end2)
			{
				tmp[i] = arr[begin2];
				begin2++;
				i++;
			}
			memcpy(arr + j, tmp + j, sizeof(int) * (end2 - j + 1));
		}
		gap *= 2;//两个小区间合并为一个大区间
	}
	free(tmp);
}

归并排序特性总结：

  • 时间复杂度：O(NlogN)

  • 空间复杂度：O(N)

  • 稳定性：稳定

  • 优势：时间复杂度稳定，适合外部排序

4.5 计数排序

计数排序先创造一个计数数组，随后对原数组的数据进行计数，例如将值为5的数据的个数放在计数数组下标为5的数据中

但这种风险极大，如单个100仍会开100个空间

我们可以使用相对映射，即100为数组中最小的数据，那么就放在第1个位置，109为最大的数据，那么就放在最后一个位置，计数数组的长度为最大数据与最小数据的差

cpp 复制代码 
void CountSort(int* a, int n) {
    // 找出最大值和最小值
    int min = a[0], max = a[0];
    for (int i = 1; i < n; i++) {
        if (a[i] < min) min = a[i];
        if (a[i] > max) max = a[i];
    }
    
    int range = max - min + 1;
    int* count = (int*)calloc(range, sizeof(int));
    
    // 统计每个元素出现的次数
    for (int i = 0; i < n; i++) {
        count[a[i] - min]++;
    }
    
    // 根据计数数组重构原数组
    int j = 0;
    for (int i = 0; i < range; i++) {
        while (count[i]--) {
            a[j++] = i + min;
        }
    }
    
    free(count);
}

计数排序特性总结：

  • 时间复杂度：O(N + range)

  • 空间复杂度：O(range)

  • 稳定性：稳定

  • 适用场景：数据范围不大且为整数的情况

4.6 性能对比

排序方法 平均情况 最好情况 最坏情况 空间复杂度 稳定性
冒泡排序 O(N²) O(N) O(N²) O(1) 稳定
直接选择排序 O(N²) O(N²) O(N²) O(1) 不稳定
直接插入排序 O(N²) O(N) O(N²) O(1) 稳定
希尔排序 O(N¹·³) O(N) O(N²) O(1) 不稳定
堆排序 O(NlogN) O(NlogN) O(NlogN) O(1) 不稳定
快速排序 O(NlogN) O(NlogN) O(N²) O(logN) 不稳定
归并排序 O(NlogN) O(NlogN) O(NlogN) O(N) 稳定
计数排序 O(N+range) O(N+range) O(N+range) O(range) 稳定

如何选择合适的排序算法

  1. 数据量小：直接插入排序、冒泡排序

  2. 数据基本有序：直接插入排序

  3. 数据量中等：希尔排序、堆排序

  4. 数据量大且要求稳定：归并排序

  5. 数据量大且不要求稳定：快速排序

  6. 数据为整数且范围不大：计数排序

  7. 外部排序：归并排序

5. STL常见的容器

STL (Standard Template Library) 是C++标准库的核心组成部分，提供了一套通用的模板类和函数，实现了常见的数据结构和算法

这里我们复习STL中的容器

5.1 序列式容器

5.1.1 string

string严格来说不属于STL，其存在于STL之前，但由于和STL又极其相似，因此我们还是纳入进来

5.1.1.1 构建string
cpp 复制代码 
string s1;              // 空字符串
string s2("hello");     // 用C字符串构造
string s3(s2);          // 拷贝构造
string s4(5, 'A');      // "AAAAA"
string s5 = "world";    // 赋值构造
5.1.1.2 容量操作

size（重点） 返回字符串有效字符长度

length 返回字符串有效字符长度

capacity 返回空间总大小

empty （重点） 检测字符串释放为空串，是返回true，否则返回false

clear （重点） 清空有效字符

reserve （重点）为字符串预留空间**

resize （重点） 将有效字符的个数该成n个，多出的空间用字符c填充

cpp 复制代码 
string str = "hello";
cout << str.size();     // 5，返回有效字符长度
cout << str.length();   // 5，与size()相同
cout << str.capacity(); // 返回总容量
cout << str.empty();    // 是否为空

str.clear();            // 清空字符串
str.resize(10, 'x');    // 调整大小，多出部分用'x'填充
str.reserve(100);       // 预留空间，提高效率
5.1.1.3 string的修改操作

push_back在字符串后尾插字符c

cpp 复制代码 
str.push_back('!');     // 尾部添加字符

append 在字符串后追加一个字符串

cpp 复制代码 
str.append(" world");   // 追加字符串

**operator+=**在字符串后追加字符串str

cpp 复制代码 
str += "!!!";           // 最常用的追加方式

c_str 返回C格式字符串

find 从字符串pos位置开始往后找字符c/字符串，返回该字符在字符串中的位置

cpp 复制代码 
size_t pos = str.find("world");    // 查找子串

substr 在str中从pos位置开始，截取n个字符，然后将其返

cpp 复制代码 
if (pos != string::npos) {
    string sub = str.substr(pos, 5); // 截取子串
}

erase 删除子串

cpp 复制代码 
str.erase(5, 4);// 删除子串(从起始地点为5的位置开始删除4个字符)
5.1.1.4 访问和遍历

string重载了operator[]，使其能够像操作数组一样利用[]来访问元素

cpp 复制代码 
int main ()
{
  std::string str ("Test string");
  for (int i=0; i<str.length(); ++i)
  {
    std::cout << str[i];//利用[]和下标来访问元素
  }
  return 0;
}

begin获取一个字符的迭代器 + end获取最后一个字符下一个位置的迭代器

cpp 复制代码 
string str = "hello";
 
 
// 迭代器
for (auto it = str.begin(); it != str.end(); ++it) {
    cout << *it;//从左到右访问->hello
}

5.1.2 vector

vector是C++标准库中的一个序列容器，它封装了动态大小数组的功能。主要特点包括：

  • 动态扩容：根据需要自动调整容量

  • 随机访问：支持通过下标直接访问元素，时间复杂度O(1)

  • 连续存储：元素在内存中连续存放，缓存友好

  • 类型安全：模板化设计，编译时类型检查

5.1.2.1 构造vector

vector的构造和string基本一致

cpp 复制代码 
#include <vector>
using namespace std;

// 1. 默认构造 - 空vector
vector<int> v1;

// 2. 构造包含n个val的vector
vector<int> v2(5, 10);  // {10, 10, 10, 10, 10}

// 3. 拷贝构造
vector<int> v3(v2);     // 与v2相同

// 4. 使用迭代器范围构造
int arr[] = {1, 2, 3, 4, 5};
vector<int> v4(arr, arr + 5);  // {1, 2, 3, 4, 5}

// 5. 初始化列表构造 (C++11)
vector<int> v5 = {1, 2, 3, 4, 5};
5.1.2.2 容量管理

| 容量空间 | 接口说明 |
| size | 获取数据个数 |
| capacity | 获取容量大小 |
| empty | 判断是否为空 |
| resize | 改变vector的size |

reserve 改变vector的capacity

reserve

如果 n 大于当前容量，则该函数会导致容器重新分配其存储，将其容量增加到 n （或更大）。

在所有其他情况下(即n小于或等于当前容量)，函数调用不会导致重新分配，并且容量不受影响。

resize

如果 n 小于当前容器大小，则内容将减少到其前 n 个 元素，删除超出的元素（并销毁它们）。

如果 n 大于当前容器大小，则通过在末尾插入所需数量的元素来扩展内容，以达到 n 的大小。如果指定了 val ，则新元素将初始化为 val 的副本，否则，它们将被值初始化。

如果 n 也大于当前容器容量，则会自动重新分配已分配的存储空间。

5.1.2.3 元素访问
元素访问 接口说明
operator[] 数组下标访问
front 数组第一个元素
back 数组最后一个元素
data 数组地址
cpp 复制代码 
vector<int> v = {1, 2, 3, 4, 5};

// 下标访问
cout << v[0];           // 1 (不检查边界)

// 首尾元素访问
cout << v.front();      // 1
cout << v.back();       // 5

// 数据指针
int* data = v.data();   // 获取底层数组指针
5.1.2.4 修改操作

| vector增删查改 | 接口说明 |
| push_back（重点） | 尾插 |
| pop_back（重点） | 尾删 |
| find | 查找。（注意这个是算法模块实现，不是vector的成员接口） |
| insert | 在position之前插入val |
| erase | 删除position位置的数据 |

swap 交换两个vector的数据空间
cpp 复制代码 
vector<int> v = {1, 2, 3};

// 尾部操作
v.push_back(4);         // {1, 2, 3, 4}
v.pop_back();           // {1, 2, 3}

// 插入操作
v.insert(v.begin() + 1, 10);  // {1, 10, 2, 3}

// 删除操作
v.erase(v.begin() + 1);       // {1, 2, 3}
v.erase(v.begin(), v.begin() + 2); // {3}


// 交换
vector<int> v2 = {4, 5, 6};
v.swap(v2);             // 交换两个vector的内容

find(v.begin(),v.end(),2)//algorithm库中的函数，查找对应值的数据

5.1.3 list

list是C++标准库中的一个序列容器，它基于带头节点的双向循环链表实现。主要特点包括：

  • 双向遍历：支持从前向后和从后向前的遍历

  • 高效插入删除：在任意位置插入删除元素的时间复杂度为O(1)

  • 非连续存储：元素在内存中分散存储，无扩容开销

  • 迭代器稳定性：插入操作不会使迭代器失效

5.1.3.1 构造list

list和srting，vector的构造极为相似

cpp 复制代码 
#include <list>
using namespace std;

// 1. 默认构造 - 空list
list<int> l1;

// 2. 构造包含n个val的list
list<int> l2(5, 10);  // {10, 10, 10, 10, 10}

// 3. 拷贝构造
list<int> l3(l2);     // 与l2相同

// 4. 使用迭代器范围构造
int arr[] = {1, 2, 3, 4, 5};
list<int> l4(arr, arr + 5);  // {1, 2, 3, 4, 5}

// 5. 初始化列表构造 (C++11)
list<int> l5 = {1, 2, 3, 4, 5};
5.1.3.2 迭代器使用

集成后的迭代器可像string和vector那样使用

cpp 复制代码 
list<int> lst = {1, 2, 3, 4, 5};

// 正向迭代器
cout << "正向遍历: ";
for (auto it = lst.begin(); it != lst.end(); ++it) {
    cout << *it << " ";  // 1 2 3 4 5
}

// 反向迭代器
cout << "\n反向遍历: ";
for (auto rit = lst.rbegin(); rit != lst.rend(); ++rit) {
    cout << *rit << " ";  // 5 4 3 2 1
}

// 范围for循环
cout << "\n范围for: ";
for (auto& elem : lst) {
    cout << elem << " ";
}

注意 ：list的迭代器是双向迭代器 ，不支持随机访问，不能进行it + n操作。

5.1.3.3 容量操作

list没有capacity容量的概念，只有size有效节点个数的概念

cpp 复制代码 
list<int> lst = {1, 2, 3};

cout << lst.size();        // 元素个数: 3
cout << lst.empty();       // 是否为空: false
cout << lst.max_size();    // 理论最大容量

// list没有capacity概念，因为不需要预分配空间
5.1.3.4 元素访问

list不是线性的，不能使用[]下标来访问数据

cpp 复制代码 
list<int> lst = {1, 2, 3, 4, 5};

// 访问首尾元素
cout << lst.front();      // 1
cout << lst.back();       // 5

// 注意：list不支持下标访问！
// cout << lst[0];       // 错误！编译不通过
5.1.3.5 修改操作

list的增删查改与string,vector也基本一致

cpp 复制代码 
list<int> lst = {1, 2, 3};

// 头部操作
lst.push_front(0);        // {0, 1, 2, 3}
lst.pop_front();          // {1, 2, 3}

// 尾部操作
lst.push_back(4);         // {1, 2, 3, 4}
lst.pop_back();           // {1, 2, 3}

// 插入操作
auto it = lst.begin();
++it;                     // 指向第二个元素
lst.insert(it, 10);       // {1, 10, 2, 3}

// 删除操作
it = lst.begin();
++it;                     // 指向10
lst.erase(it);            // {1, 2, 3}

// 清空
lst.clear();              // {}

// 交换
list<int> lst2 = {4, 5, 6};
lst.swap(lst2);           // 交换两个list的内容
5.1.3.6 list特有操作

list不受连续空间的限制，相对自由且高效

cpp 复制代码 
list<int> lst1 = {1, 3, 5};
list<int> lst2 = {2, 4, 6};

// 合并两个有序链表（lst2会被清空）
lst1.merge(lst2);         // lst1: {1, 2, 3, 4, 5, 6}, lst2: {}

// 排序
list<int> lst3 = {3, 1, 4, 2};
lst3.sort();              // {1, 2, 3, 4}

// 去重（需要先排序）
list<int> lst4 = {1, 2, 2, 3, 3, 3};
lst4.unique();            // {1, 2, 3}

// 反转
list<int> lst5 = {1, 2, 3};
lst5.reverse();           // {3, 2, 1}

// 拼接：将另一个list的部分元素移动到当前list
list<int> lst6 = {1, 2, 3};
list<int> lst7 = {4, 5, 6};
auto pos = lst6.begin();
++pos;                    // 指向2
lst6.splice(pos, lst7);   // lst6: {1, 4, 5, 6, 2, 3}, lst7: {}

5.1.4 deque

deque(双端队列)：是一种双开口的"连续"空间的数据结构，双开口的含义是：可以在头尾两端 进行插入和删除操作，且时间复杂度为O(1)，与vector比较，头插效率高，不需要搬移元素；与 list比较，空间利用率比较高。

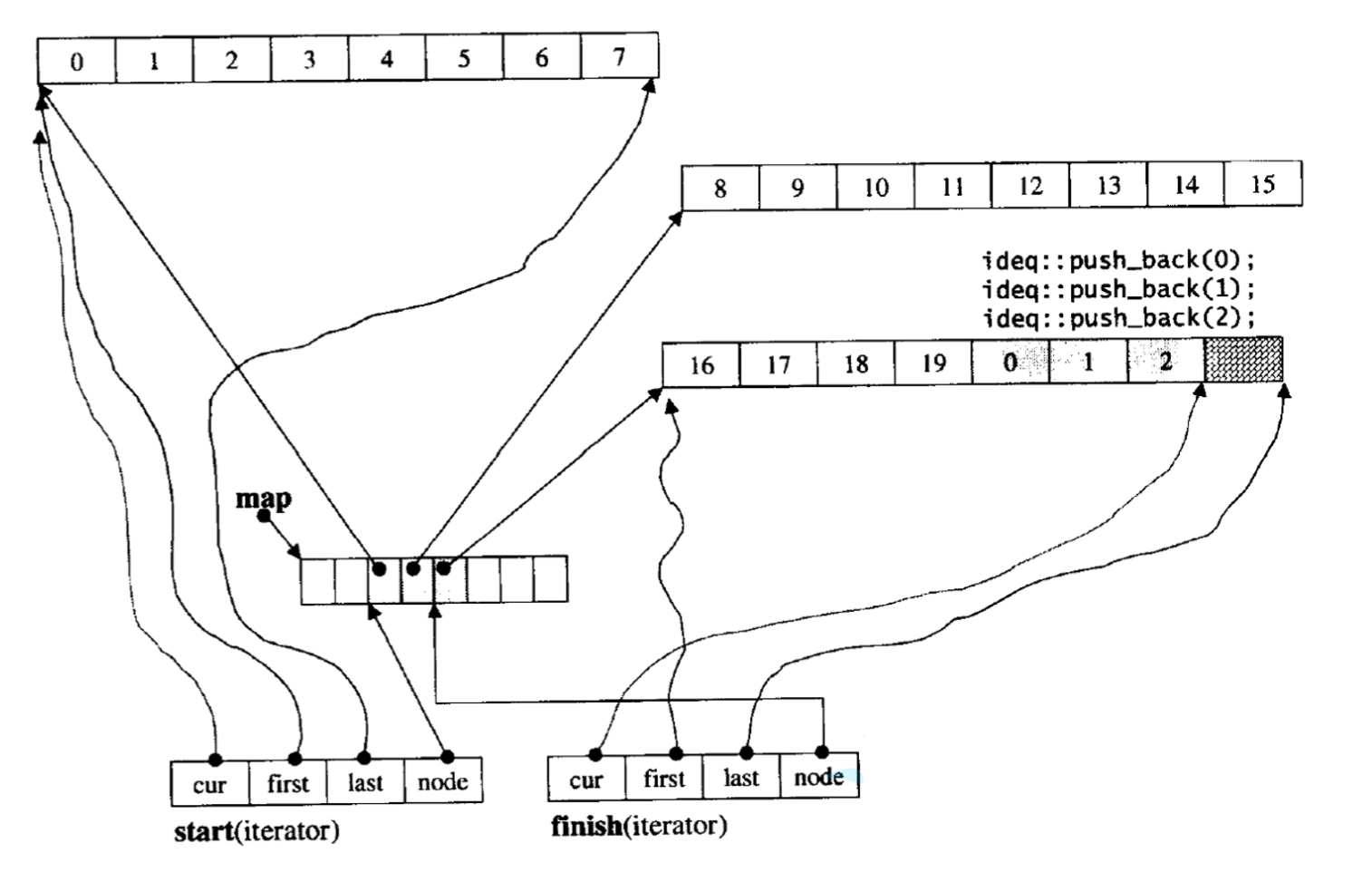
deque先是由一个中控台(map)构成，每个中控台节点包含cur,first,last,node四个指针

first代表一个数组的首地址

last代表一个数组的尾地址

cur则用来遍历数组中的元素

node代表该中控台节点的位置

因此deque结合了list和vector的优点，相当于几个数组 以链表的形式连接起来

选择deque的原因：

  1. 综合性能优秀：

    • 头部尾部操作都是O(1)

    • 不需要vector的扩容拷贝开销

    • 比list缓存友好，内存局部性更好

  2. 适合适配器需求：

    • stack只需要push_back、pop_back、back

    • queue需要push_back、pop_front、front、back

    • deque完美支持这些操作

  3. 内存效率：

    • 分段连续存储，扩容代价小

    • 空间利用率高于list

5.1.5 序列式容器对比

操作 vector deque list forward_list array
随机访问 O(1) O(1) O(n) O(n) O(1)
头部插入 O(n) O(1) O(1) O(1) 不支持
尾部插入 O(1) O(1) O(1) O(n) 不支持
中间插入 O(n) O(n) O(1) O(1) 不支持
头部删除 O(n) O(1) O(1) O(1) 不支持
尾部删除 O(1) O(1) O(1) O(n) 不支持
内存连续性 连续 分段连续 不连续 不连续 连续
额外开销 小 中 大 中 无

5.2 关联式容器

STL中的关联式容器分为两大类：

有序关联容器（基于红黑树）

  • set - 有序集合，元素唯一

  • multiset - 有序集合，元素可重复

  • map - 有序键值对，键唯一

  • multimap - 有序键值对，键可重复

无序关联容器（基于哈希表，C++11）

  • unordered_set - 无序集合，元素唯一

  • unordered_multiset - 无序集合，元素可重复

  • unordered_map - 无序键值对，键唯一

  • unordered_multimap - 无序键值对，键可重复

无序和有序的容器使用方式几乎没有差别，我们在这里只讨论有序容器

5.2.1 set

set是一个关键字的集合，底层用红黑树实现，具有以下特性：

  • 元素自动排序（默认升序）
  • 元素唯一（不允许重复）
  • 查找、插入、删除时间复杂度为O(logN)
5.2.1.1 构造set

set提供多种构造方式：

cpp 复制代码 
// 默认构造
set<int> s1;

// 迭代器区间构造
vector<int> v = {1, 2, 3};
set<int> s2(v.begin(), v.end());

// 拷贝构造
set<int> s3(s2);

// 初始化列表构造
set<int> s4 = {1, 2, 3, 4, 5};
5.2.1.2 set的迭代器

set支持双向迭代器，遍历时按关键字升序排列：

cpp 复制代码 
set<int> s = {5, 2, 7, 1, 9};

// 正向遍历
for(auto it = s.begin(); it != s.end(); ++it) {
    cout << *it << " ";  // 输出：1 2 5 7 9
}

// 反向遍历  
for(auto it = s.rbegin(); it != s.rend(); ++it) {
    cout << *it << " ";  // 输出：9 7 5 2 1
}

// 范围for循环
for(const auto& elem : s) {
    cout << elem << " ";
}

重要特性：set的iterator和const_iterator都不支持修改元素值，因为修改关键字会破坏红黑树的结构。

5.2.1.3 set的增删查操作

都是STL的容器,set的增删查基本和其他的STL容器一样

插入

需要注意的是，set无法插入已有的相同数据，例如插入了2，那么就不能再插入2这个数据

cpp 复制代码 
set<int> s;

// 单个插入
auto result1 = s.insert(5);  // 返回pair<iterator, bool>

// 初始化列表插入
s.insert({2, 7, 5});  // 5已存在，插入失败

// 迭代器区间插入
vector<int> v = {1, 8, 3};
s.insert(v.begin(), v.end());

查找

cpp 复制代码 
set<int> s = {4, 2, 7, 2, 8, 5, 9};

// find查找，返回迭代器
auto it = s.find(5);
if(it != s.end()) {
    cout << "找到元素：" << *it << endl;
}

// count计数（对于set，只能是0或1）
if(s.count(5)) {
    cout << "元素存在" << endl;
}

// 算法库的find（不推荐，效率低）
auto pos = find(s.begin(), s.end(), 5);  // O(N)复杂度

删除

cpp 复制代码 
set<int> s = {4, 2, 7, 2, 8, 5, 9};

// 通过迭代器删除
s.erase(s.begin());  // 删除最小元素

// 通过值删除
int num = s.erase(5);  // 返回删除的元素个数

// 删除区间
auto it_low = s.lower_bound(3);  // >=3的第一个元素
auto it_up = s.upper_bound(7);   // >7的第一个元素  
s.erase(it_low, it_up);          // 删除[3, 7]区间

5.2.2 map

map是键值对（key-value）的集合，底层同样用红黑树实现：

特性：

  • 按key自动排序
  • key唯一
  • 支持通过key快速查找value
  • 查找、插入、删除时间复杂度O(logN)
5.2.2.1 构造map
cpp 复制代码 
int main() {
    // 初始化列表构造
    map<string, string> dict = {
        {"left", "左边"}, 
        {"right", "右边"},
        {"insert", "插入"}, 
        {"string", "字符串"}
    };
    
    // 迭代器遍历
    auto it = dict.begin();
    while(it != dict.end()) {
        cout << it->first << ":" << it->second << endl;
        ++it;
    }
    
    // 插入pair的多种方式
    pair<string, string> kv1("first", "第一个");
    dict.insert(kv1);
    dict.insert(pair<string, string>("second", "第二个"));
    dict.insert(make_pair("sort", "排序"));
    dict.insert({"auto", "自动的"});
    
    // "left"已存在，插入失败
    dict.insert({"left", "左边，剩余"});
}
5.2.2.2 map的迭代器

map的迭代器解引用得到的是pair，使用时要分清时访问key还是value

cpp 复制代码 
  // 范围for遍历
    for(const auto& e : dict) {
        cout << e.first << ":" << e.second << endl;
    }
    
    return 0;

5.2.2.3 map的operator[]

map最重要的特性之一是operator[]，它兼具查找、插入、修改功能。但set没有

因为map的[]本质是获取value而不是key，key不能被修改。

cpp 复制代码 
map<string, string> dict;

// key不存在 -> 插入 {"insert", string()}
dict["insert"];

// 插入+修改
dict["left"] = "左边";

// 修改
dict["left"] = "左边、剩余";

// key存在 -> 查找
cout << dict["left"] << endl;  // 输出：左边、剩余

需要注意的是，如果[]访问的那个元素不存在，那么就会自动插入进去

因此[]就相当于继承了find和insert的功能，先find，找到了就直接返回value，如果没找到那么就insert

5.3 容器适配器

5.3.1 容器适配器的概念

容器适配器是基于其他容器实现的包装类 ，它们提供特定的接口，隐藏底层容器的实现细节，为特定应用场景提供专门的数据结构操作方式。

核心特点：

  • 不是独立的容器：基于现有容器（如deque、vector）实现

  • 接口受限：只暴露特定操作，隐藏其他功能

  • 行为特定：每种适配器有特定的数据访问规则

  • 底层容器可定制：可以指定使用哪种底层容器

5.3.2 STL中的三种容器适配器

5.3.2.1 stack

基本概念

  • LIFO (Last-In-First-Out) - 后进先出

  • 默认底层容器：deque

  • 可用底层容器：deque、vector、list

常用接口

cpp 复制代码 
#include <stack>
#include <iostream>

void stackExample() {
    // 创建栈
    std::stack<int> s1;                    // 默认使用deque
    std::stack<int, std::vector<int>> s2;  // 使用vector作为底层容器
    std::stack<int, std::list<int>> s3;    // 使用list作为底层容器
    
    // 元素访问
    s1.push(1);              // 压栈
    s1.push(2);
    s1.push(3);
    
    std::cout << "栈顶元素: " << s1.top() << std::endl;  // 3
    std::cout << "栈大小: " << s1.size() << std::endl;   // 3
    
    s1.pop();                // 弹栈
    std::cout << "弹栈后栈顶: " << s1.top() << std::endl; // 2
    
    // 容量操作
    std::cout << "是否为空: " << s1.empty() << std::endl; // 0 (false)
    
    // 交换
    std::stack<int> other;
    other.push(99);
    s1.swap(other);
    std::cout << "交换后栈顶: " << s1.top() << std::endl; // 99
}
5.3.2.2 queue

基本概念

  • FIFO (First-In-First-Out) - 先进先出

  • 默认底层容器：deque

  • 可用底层容器：deque、list

常用接口

cpp 复制代码 
#include <queue>
#include <iostream>

void queueExample() {
    // 创建队列
    std::queue<int> q1;                   // 默认使用deque
    std::queue<int, std::list<int>> q2;   // 使用list作为底层容器
    
    // 元素操作
    q1.push(1);              // 入队
    q1.push(2);
    q1.push(3);
    
    std::cout << "队首元素: " << q1.front() << std::endl; // 1
    std::cout << "队尾元素: " << q1.back() << std::endl;  // 3
    std::cout << "队列大小: " << q1.size() << std::endl;  // 3
    
    q1.pop();                // 出队
    std::cout << "出队后队首: " << q1.front() << std::endl; // 2
    
    // 容量操作
    std::cout << "是否为空: " << q1.empty() << std::endl; // 0 (false)
    
    // 注意：queue没有clear()方法，但可以这样清空
    std::queue<int> empty;
    std::swap(q1, empty);
    std::cout << "清空后大小: " << q1.size() << std::endl; // 0
}
5.3.2.3 priority_queue

基本概念

  • 元素按优先级出队，默认最大元素优先（大顶堆）

  • 默认底层容器：vector

  • 可用底层容器：vector、deque

  • 需要比较函数：默认std::less，创建大顶堆

常用接口

cpp 复制代码 
#include <queue>
#include <iostream>
#include <vector>
#include <functional>

void priorityQueueExample() {
    // 创建优先队列
    std::priority_queue<int> pq1;                          // 默认大顶堆
    std::priority_queue<int, std::vector<int>> pq2;        // 显式指定vector
    std::priority_queue<int, std::vector<int>, std::greater<int>> pq3; // 小顶堆
    
    // 元素操作
    pq1.push(3);
    pq1.push(1);
    pq1.push(4);
    pq1.push(1);
    pq1.push(5);
    
    std::cout << "优先队列大小: " << pq1.size() << std::endl; // 5
    std::cout << "队首元素(最大): " << pq1.top() << std::endl; // 5
    
    // 按优先级顺序出队
    std::cout << "出队顺序: ";
    while (!pq1.empty()) {
        std::cout << pq1.top() << " ";  // 5, 4, 3, 1, 1
        pq1.pop();
    }
    std::cout << std::endl;
    
    // 小顶堆示例
    pq3.push(3);
    pq3.push(1);
    pq3.push(4);
    
    std::cout << "小顶堆出队顺序: ";
    while (!pq3.empty()) {
        std::cout << pq3.top() << " ";  // 1, 3, 4
        pq3.pop();
    }
    std::cout << std::endl;
}

6. STL的迭代器

迭代器是指向容器元素的智能指针 ，提供了一种统一的方法来遍历和访问容器中的元素，隐藏了底层容器的实现细节。

6.1迭代器分类

迭代器类型 支持操作 对应容器
输入迭代器 只读，单次遍历 istream
输出迭代器 只写，单次遍历 ostream
前向迭代器 读写，多次遍历 forward_list, unordered_*
双向迭代器 前后移动 list, set, map
随机访问迭代器 任意跳转 vector, deque, array, string

6.2 迭代器的基本使用

6.2.1 获取迭代器

cpp 复制代码 
#include <vector>
#include <list>
#include <set>
#include <iostream>

void iteratorBasics() {
    std::vector<int> vec = {1, 2, 3, 4, 5};
    std::list<std::string> lst = {"apple", "banana", "cherry"};
    std::set<int> s = {3, 1, 4, 1, 5};
    
    // 获取迭代器
    auto vec_begin = vec.begin();      // 指向第一个元素
    auto vec_end = vec.end();          // 指向尾后位置
    
    auto lst_begin = lst.begin();
    auto lst_end = lst.end();
    
    auto s_begin = s.begin();
    auto s_end = s.end();
    
    // 常量迭代器
    auto vec_cbegin = vec.cbegin();    // 只读迭代器
    auto vec_cend = vec.cend();
    
    // 反向迭代器（双向和随机访问容器）
    auto vec_rbegin = vec.rbegin();    // 指向最后一个元素
    auto vec_rend = vec.rend();        // 指向首前位置
}

6.2.2 遍历容器

cpp 复制代码 
void traversalExamples() {
    std::vector<int> vec = {1, 2, 3, 4, 5};
    
    // 方法1：传统迭代器遍历
    std::cout << "传统迭代器: ";
    for (auto it = vec.begin(); it != vec.end(); ++it) {
        std::cout << *it << " ";
    }
    std::cout << std::endl;
    
    // 方法2：基于范围的for循环 (C++11) - 推荐！
    std::cout << "范围for循环: ";
    for (const auto& elem : vec) {
        std::cout << elem << " ";
    }
    std::cout << std::endl;
    
    // 方法3：反向遍历
    std::cout << "反向遍历: ";
    for (auto rit = vec.rbegin(); rit != vec.rend(); ++rit) {
        std::cout << *rit << " ";
    }
    std::cout << std::endl;
    
    // 方法4：使用迭代器算法
    std::cout << "使用算法: ";
    std::for_each(vec.begin(), vec.end(), [](int x) {
        std::cout << x << " ";
    });
    std::cout << std::endl;
}

6.2.3 迭代器操作

cpp 复制代码 
void iteratorOperations() {
    std::vector<int> vec = {10, 20, 30, 40, 50};
    
    // 解引用
    auto it = vec.begin();
    std::cout << "第一个元素: " << *it << std::endl; // 10
    
    // 指针运算（随机访问迭代器）
    it = it + 2;                    // 移动到第三个元素
    std::cout << "第三个元素: " << *it << std::endl; // 30
    
    it = vec.end() - 1;             // 移动到最后一个元素
    std::cout << "最后一个元素: " << *it << std::endl; // 50
    
    // 比较迭代器
    if (vec.begin() < vec.end()) {
        std::cout << "begin在end之前" << std::endl;
    }
    
    // 距离计算
    auto dist = std::distance(vec.begin(), vec.end());
    std::cout << "元素个数: " << dist << std::endl; // 5
    
    // 双向迭代器操作（list示例）
    std::list<int> lst = {1, 2, 3};
    auto lit = lst.begin();
    ++lit; // 前进
    --lit; // 后退（双向迭代器特有）
    
    // 前向迭代器操作（forward_list示例）
    std::forward_list<int> flst = {1, 2, 3};
    auto fit = flst.begin();
    ++fit; // 只能前进，不能后退
}

6.3 迭代器失效问题

当容器发生结构性修改 （插入、删除元素）时，指向容器元素的迭代器可能变得无效 ，继续使用会导致未定义行为。

6.3.1 各容器迭代器失效情况

vector 和 string
cpp 复制代码 
void vectorIteratorInvalidation() {
    std::vector<int> vec = {1, 2, 3, 4, 5};
    auto it = vec.begin() + 2;  // 指向3
    
    // 情况1：在it之前插入 - it失效
    vec.insert(vec.begin() + 1, 99);
    // std::cout << *it << std::endl; // 未定义行为！
    
    // 情况2：在it之后插入 - 可能失效（如果重新分配）
    it = vec.begin() + 3;  // 重新获取
    vec.push_back(100);    // 可能导致重新分配
    // std::cout << *it << std::endl; // 可能失效！
    
    // 情况3：删除it指向的元素 - it失效
    it = vec.begin() + 2;
    vec.erase(it);
    // std::cout << *it << std::endl; // 未定义行为！
    
    // 情况4：删除it之前的元素 - it失效
    it = vec.begin() + 3;
    vec.erase(vec.begin() + 1);
    // std::cout << *it << std::endl; // 未定义行为！
}
list 和 forward_list
cpp 复制代码 
void listIteratorInvalidation() {
    std::list<int> lst = {1, 2, 3, 4, 5};
    auto it = std::next(lst.begin(), 2);  // 指向3
    
    // 情况1：插入元素 - 不会使其他迭代器失效
    lst.insert(lst.begin(), 0);  // it仍然有效
    std::cout << "*it = " << *it << std::endl; // 3
    
    // 情况2：删除其他元素 - 不会使it失效
    lst.erase(lst.begin());      // it仍然有效
    std::cout << "*it = " << *it << std::endl; // 3
    
    // 情况3：删除it指向的元素 - it失效
    auto to_delete = it;
    ++it;  // 先移动迭代器！
    lst.erase(to_delete);
    std::cout << "*it = " << *it << std::endl; // 4（it仍然有效）
    
    // forward_list类似，但只有前向迭代器
    std::forward_list<int> flst = {1, 2, 3};
    auto fit = std::next(flst.begin());  // 指向2
    flst.erase_after(flst.begin());      // 删除2
    // std::cout << *fit << std::endl;   // 失效！
}
关联容器（set, map, multiset, multimap）
cpp 复制代码 
void associativeIteratorInvalidation() {
    std::set<int> s = {1, 2, 3, 4, 5};
    auto it = s.find(3);  // 指向3
    
    // 情况1：插入元素 - 不会使迭代器失效
    s.insert(6);  // it仍然有效
    std::cout << "*it = " << *it << std::endl; // 3
    
    // 情况2：删除其他元素 - 不会使it失效
    s.erase(1);   // it仍然有效
    std::cout << "*it = " << *it << std::endl; // 3
    
    // 情况3：删除it指向的元素 - it失效
    auto to_delete = it;
    ++it;  // 先移动迭代器！
    s.erase(to_delete);
    std::cout << "*it = " << *it << std::endl; // 4（it仍然有效）
    
    // unordered_* 容器在重新哈希时所有迭代器失效
    std::unordered_set<int> us = {1, 2, 3};
    auto uit = us.find(2);
    us.rehash(100);  // 重新哈希
    // std::cout << *uit << std::endl; // 失效！
}

6.3.2 避免迭代器失效的策略

修改之后重新获得迭代器
cpp 复制代码 
 static void reacquireIterators() {
        std::vector<int> vec = {1, 2, 3, 4, 5};
        auto it = vec.begin() + 2;  // 指向3
        
        // 插入操作后重新获取
        vec.insert(vec.begin() + 1, 99);
        it = vec.begin() + 3;  // 重新获取，现在指向3
        
        std::cout << "安全访问: " << *it << std::endl; // 3
    }
索引代替迭代器
cpp 复制代码 
  static void useIndices() {
        std::vector<int> vec = {1, 2, 3, 4, 5};
        size_t index = 2;  // 记录位置而不是迭代器
        
        vec.insert(vec.begin() + 1, 99);  // 插入操作
        // index现在对应元素3的位置变成了3
        
        if (index < vec.size()) {
            std::cout << "安全访问: " << vec[index] << std::endl; // 3
        }
    }
先计算再修改
cpp 复制代码 
static void calculateThenModify() {
        std::vector<int> vec = {1, 2, 3, 4, 5};
        
        // 先收集需要删除的索引
        std::vector<size_t> to_remove;
        for (size_t i = 0; i < vec.size(); ++i) {
            if (vec[i] % 2 == 0) {  // 删除偶数
                to_remove.push_back(i);
            }
        }

结束语

C++ 从入门到入坟也是结束了。但到最后，我们到底是入门了还是入坟了呢?不好说，但我相信，能跟到现在的你，绝对不差。

这个世界上没有什么特别难的事,C++很难吗？好像确实有一定难度，但难度不是门槛，而是时间和耐心的考验。你只要有耐心，愿意去花时间，那么攻克这些难题只是时间问题罢了

学海无涯，C++翻过了语法基础这一道坎，还有无数的山等着我们。linux?网络?高阶数据结构?

学习是停不下来的，这里不是结束，只是一个新的开始

还是祝你，祝我，祝大家都能学有所成，所想皆成，前程似锦。

C++

END...

相关推荐
REDcker7 小时前
C++项目 OpenSSL 依赖最佳实践
开发语言·c++
一念&7 小时前
每日一个C语言知识：C 错误处理
c语言·开发语言·算法
大白的编程日记.8 小时前
计算机网络学习笔记】初始网络之网络发展和OSI七层模型
笔记·学习·计算机网络
qq_2816179538 小时前
MSVC 链接器处理input file的逻辑
c++
FMRbpm8 小时前
顺序表vector--------练习题3题解
数据结构·c++·新手入门
郝学胜-神的一滴8 小时前
Qt删除布局与布局切换技术详解
开发语言·数据库·c++·qt·程序人生·系统架构
奔跑吧邓邓子8 小时前
【C语言实战(66)】筑牢防线：C语言安全编码之输入与错误处理
c语言·安全·开发实战·错误处理·输入验证
buyue__8 小时前
C++实现数据结构——线性表
数据结构·c++
雨落在了我的手上9 小时前
C语言入门（十三）：操作符详解（1）
c语言
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06KGG转MP3工具|非KGM文件|解密音频07jdk21下载、安装（Windows、Linux、macOS）08GitLab 零基础入门指南：从安装到项目管理全流程09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）