
一、题目描述

二、算法原理
我们可以把数组里面的0变成-1,这样当数组前缀和0时,表示这段区域的和0和1的数量相等。
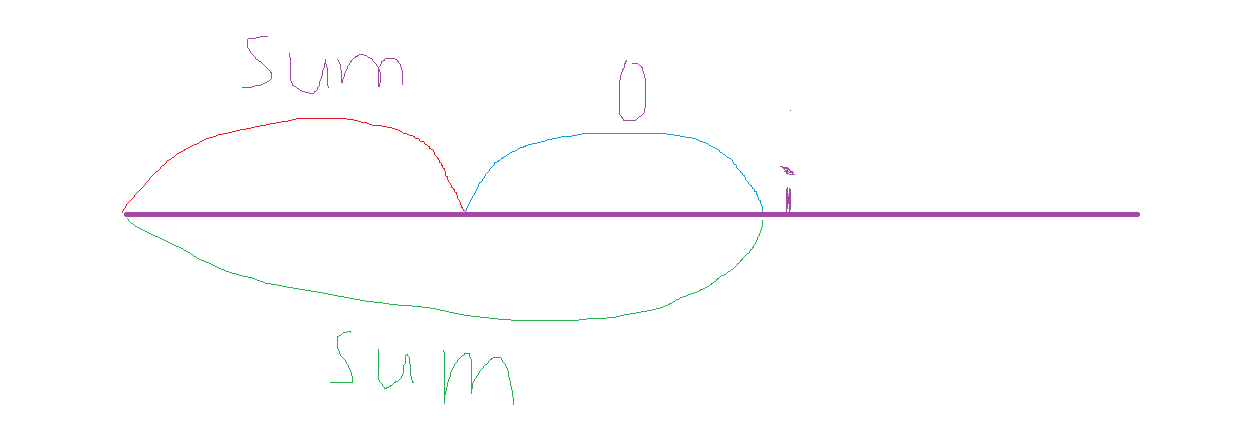
使用 hash<前缀和,数组下标>。
假设我们要计算前缀和计算到 i 点,如果我们要让 i 到前面的某个区域内和为0,那么这个区域前面要有个 sum 等于 i 点内的区域和。
特殊情况:
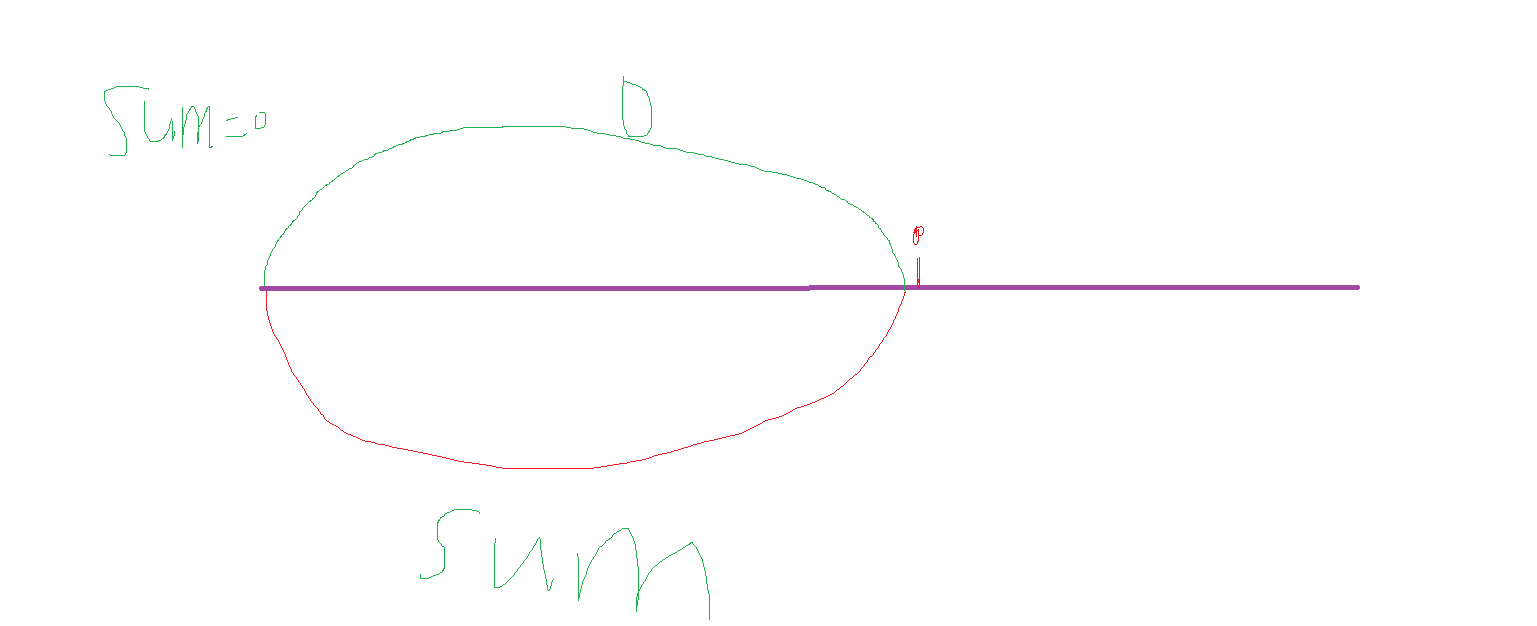
当 sum = 0 时,表示从下标 0 到 i 点的前缀和 0 和 1 的数量是相等的。但是 hash 里面没有保存 0,所以我们要提前往 hash 里面保存 hash[ 0 ] = -1。
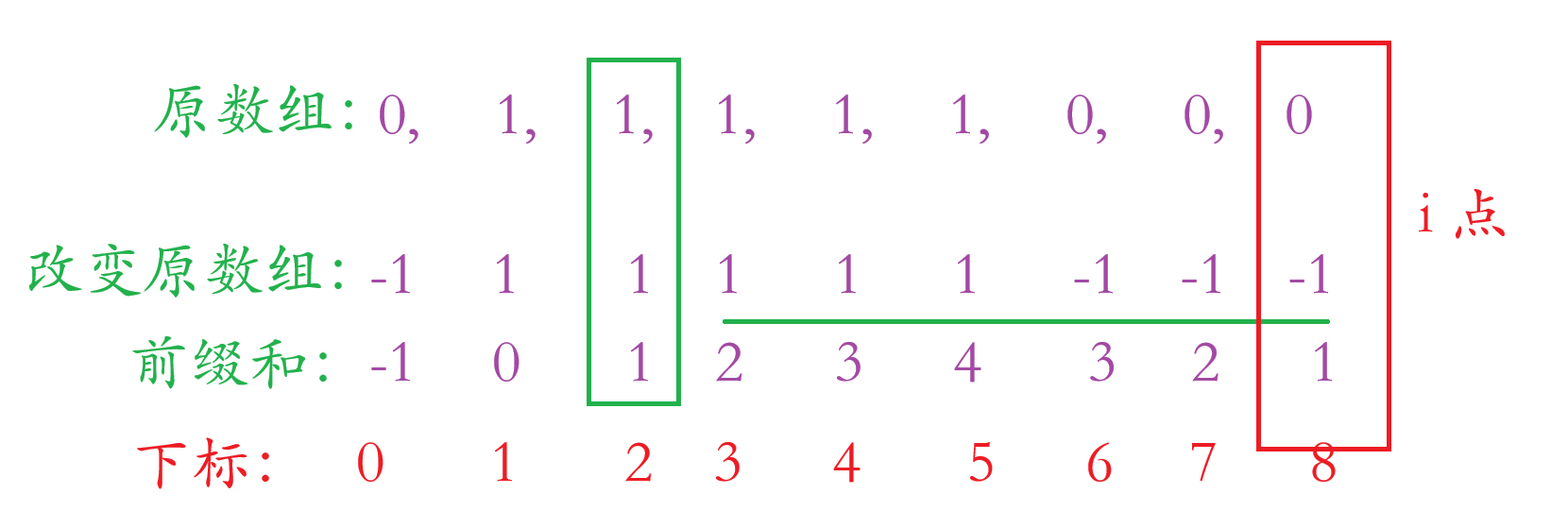
当我们求到 i 点前缀和,此时为 1,那么前面 hash 保存过 1 和他的下标 2,此时我们要计算他的长度,那么怎么计算 i 点到绿色点的长度呢?当然是 i - 绿色框住点的下标:2 = 6。
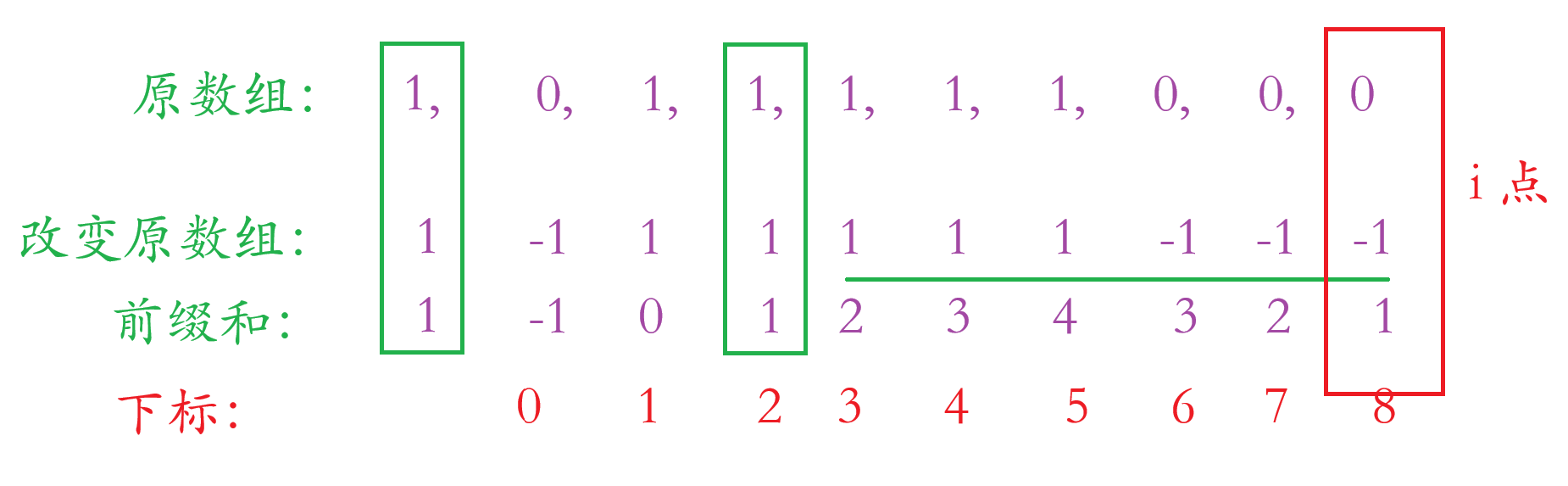
假设我们绿色框住的点有两个,问题:我们要计算 i 点到哪个绿色框住的点?
答:当然是最左边哪个,因为我们要求的是最长的那个。所以只要我们的 hash 保存过 1 就吧不要再保存了。
三、代码实现
cpp
class Solution {
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int,int> hash;
hash[0] = -1;
int sum = 0,cnt = 0;
for(int i = 0; i < nums.size();i++)
{
if(nums[i] == 0) nums[i] = -1;//把0变成-1
sum += nums[i];//计算前缀和
if(hash.count(sum)) cnt = max(cnt,i - hash[sum]);//判断最长数组
else hash[sum] = i;//入哈希
}
return cnt;
}
};