MATLAB实现模糊PID控制

MATLAB实现模糊PID控制

1.模糊PID控制

模糊PID控制是一种将传统PID控制与模糊控制思想相结合的智能控制方法。传统PID控制通过比例 (K_p)、积分 (K_i)、微分 (K_d) 参数调节系统性能，但其参数固定，难以应对对象的非线性、时变性和外界扰动，因此在复杂工况下控制性能易下降。模糊PID控制利用模糊逻辑不依赖精确数学模型的特点，根据误差 (e) 及误差变化率 (ec) 的大小和方向，采用模糊规则对PID参数进行实时自适应调整，实现在线自整定。其核心思想是通过"如果......那么......"规则将人工控制经验转化为控制策略，使系统在误差较大时增大比例和微分作用，以提高响应速度；误差较小或趋于稳定时增大积分作用，以减小稳态误差。同时，模糊推理可抑制系统超调和振荡，提高控制的稳定性和鲁棒性。因此，模糊PID控制特别适合控制对象复杂、模型难以建立或工况易变化的系统，如温度控制、电机调速、过程控制等领域，具有良好的工程应用价值。

2.MATLAB代码

%% 模糊PID控制系统仿真 - 兼容MATLAB 2024b
% 描述：实现一个复杂的模糊PID控制器，用于二阶时滞系统的控制

clear; close all; clc;
warning('off', 'all'); % 关闭警告信息

%% 1. 系统参数设置
fprintf('=== 模糊PID控制系统仿真开始 ===\n');

% 被控对象参数（二阶时滞系统）
sys_params = struct();
sys_params.K = 2.5;        % 系统增益
sys_params.tau = 0.8;      % 时间常数
sys_params.xi = 0.3;       % 阻尼比
sys_params.Td = 0.5;       % 时滞时间

% PID控制器初始参数
%%%%%%%%%%%%
加我q1579325979 有偿提供

%%%%%%%%%%%%

fprintf('系统参数初始化完成\n');

%% 2. 创建模糊逻辑系统
fprintf('创建模糊逻辑系统...\n');

% 创建新的模糊推理系统
fis = mamfis('Name', 'fuzzy_pid');

% 添加输入变量：误差e和误差变化率ec
fis = addInput(fis, [-1, 1], 'Name', 'e');    % 归一化误差
fis = addInput(fis, [-1, 1], 'Name', 'ec');   % 归一化误差变化率

% 添加输出变量：PID参数调整量
fis = addOutput(fis, [-0.3, 0.3], 'Name', 'delta_Kp');  % Kp调整量
fis = addOutput(fis, [-0.2, 0.2], 'Name', 'delta_Ki');  % Ki调整量
fis = addOutput(fis, [-0.15, 0.15], 'Name', 'delta_Kd'); % Kd调整量

% 定义输入变量e的隶属度函数
fis = addMF(fis, 'e', 'trapmf', [-1, -1, -0.6, -0.3], 'Name', 'NB'); % 负大
fis = addMF(fis, 'e', 'trimf', [-0.6, -0.3, 0], 'Name', 'NM');       % 负中
fis = addMF(fis, 'e', 'trimf', [-0.3, 0, 0.3], 'Name', 'NS');        % 负小
fis = addMF(fis, 'e', 'trimf', [-0.1, 0, 0.1], 'Name', 'ZO');        % 零
fis = addMF(fis, 'e', 'trimf', [0, 0.3, 0.6], 'Name', 'PS');         % 正小
fis = addMF(fis, 'e', 'trimf', [0.3, 0.6, 1], 'Name', 'PM');         % 正中
fis = addMF(fis, 'e', 'trapmf', [0.6, 1, 1, 1], 'Name', 'PB');       % 正大

% 定义输入变量ec的隶属度函数
fis = addMF(fis, 'ec', 'trapmf', [-1, -1, -0.6, -0.3], 'Name', 'NB');
fis = addMF(fis, 'ec', 'trimf', [-0.6, -0.3, 0], 'Name', 'NM');
fis = addMF(fis, 'ec', 'trimf', [-0.3, 0, 0.3], 'Name', 'NS');
fis = addMF(fis, 'ec', 'trimf', [-0.1, 0, 0.1], 'Name', 'ZO');
fis = addMF(fis, 'ec', 'trimf', [0, 0.3, 0.6], 'Name', 'PS');
fis = addMF(fis, 'ec', 'trimf', [0.3, 0.6, 1], 'Name', 'PM');
fis = addMF(fis, 'ec', 'trapmf', [0.6, 1, 1, 1], 'Name', 'PB');

% 定义输出变量delta_Kp的隶属度函数
fis = addMF(fis, 'delta_Kp', 'trimf', [-0.3, -0.2, -0.1], 'Name', 'NB');
fis = addMF(fis, 'delta_Kp', 'trimf', [-0.2, -0.1, 0], 'Name', 'NM');
fis = addMF(fis, 'delta_Kp', 'trimf', [-0.1, -0.05, 0], 'Name', 'NS');
fis = addMF(fis, 'delta_Kp', 'trimf', [-0.02, 0, 0.02], 'Name', 'ZO');
fis = addMF(fis, 'delta_Kp', 'trimf', [0, 0.05, 0.1], 'Name', 'PS');
fis = addMF(fis, 'delta_Kp', 'trimf', [0, 0.1, 0.2], 'Name', 'PM');
fis = addMF(fis, 'delta_Kp', 'trimf', [0.1, 0.2, 0.3], 'Name', 'PB');

% 定义输出变量delta_Ki的隶属度函数
fis = addMF(fis, 'delta_Ki', 'trimf', [-0.2, -0.15, -0.1], 'Name', 'NB');
fis = addMF(fis, 'delta_Ki', 'trimf', [-0.15, -0.1, -0.05], 'Name', 'NM');
fis = addMF(fis, 'delta_Ki', 'trimf', [-0.1, -0.05, 0], 'Name', 'NS');
fis = addMF(fis, 'delta_Ki', 'trimf', [-0.02, 0, 0.02], 'Name', 'ZO');
fis = addMF(fis, 'delta_Ki', 'trimf', [0, 0.05, 0.1], 'Name', 'PS');
fis = addMF(fis, 'delta_Ki', 'trimf', [0.05, 0.1, 0.15], 'Name', 'PM');
fis = addMF(fis, 'delta_Ki', 'trimf', [0.1, 0.15, 0.2], 'Name', 'PB');

% 定义输出变量delta_Kd的隶属度函数
fis = addMF(fis, 'delta_Kd', 'trimf', [-0.15, -0.1, -0.05], 'Name', 'NB');
fis = addMF(fis, 'delta_Kd', 'trimf', [-0.1, -0.075, -0.05], 'Name', 'NM');
fis = addMF(fis, 'delta_Kd', 'trimf', [-0.05, -0.025, 0], 'Name', 'NS');
fis = addMF(fis, 'delta_Kd', 'trimf', [-0.01, 0, 0.01], 'Name', 'ZO');
fis = addMF(fis, 'delta_Kd', 'trimf', [0, 0.025, 0.05], 'Name', 'PS');
fis = addMF(fis, 'delta_Kd', 'trimf', [0.05, 0.075, 0.1], 'Name', 'PM');
fis = addMF(fis, 'delta_Kd', 'trimf', [0.05, 0.1, 0.15], 'Name', 'PB');

%% 3. 定义模糊规则
fprintf('定义模糊规则...\n');

% 模糊规则格式：[输入1, 输入2, 输出1, 输出2, 输出3, 权重]
% 模糊集索引：1=NB, 2=NM, 3=NS, 4=ZO, 5=PS, 6=PM, 7=PB

ruleList = [
    % 当误差大时，主要目标是快速消除误差
    7, 4, 7, 1, 7, 1, 1;  % e=PB, ec=ZO -> 大幅增加Kp, 减小Ki, 大幅增加Kd
    1, 4, 1, 7, 1, 1, 1;  % e=NB, ec=ZO -> 大幅减小Kp, 增加Ki, 减小Kd

    % 当误差中等时，注重响应速度和稳定性平衡
    6, 4, 6, 2, 6, 1, 1;  % e=PM, ec=ZO -> 增加Kp, 适当减小Ki, 增加Kd
    2, 4, 2, 6, 2, 1, 1;  % e=NM, ec=ZO -> 减小Kp, 适当增加Ki, 减小Kd

    % 当误差小时，注重消除稳态误差和防止超调
    5, 4, 5, 3, 5, 1, 1;  % e=PS, ec=ZO -> 适当增加Kp, 保持Ki, 适当增加Kd
    3, 4, 3, 5, 3, 1, 1;  % e=NS, ec=ZO -> 适当减小Kp, 保持Ki, 适当减小Kd

    % 考虑误差变化率的影响
    4, 7, 4, 1, 7, 1, 1;  % e=ZO, ec=PB -> 保持Kp, 减小Ki, 增加Kd
    4, 1, 4, 7, 1, 1, 1;  % e=ZO, ec=NB -> 保持Kp, 增加Ki, 减小Kd

    % 误差和误差变化率同号时
    7, 7, 6, 1, 7, 1, 1;  % e=PB, ec=PB -> 增加Kp, 大幅减小Ki, 大幅增加Kd
    1, 1, 2, 7, 1, 1, 1;  % e=NB, ec=NB -> 减小Kp, 大幅增加Ki, 减小Kd

    % 误差和误差变化率异号时
    7, 1, 7, 7, 4, 1, 1;  % e=PB, ec=NB -> 大幅增加Kp, 大幅增加Ki, 保持Kd
    1, 7, 1, 1, 6, 1, 1;  % e=NB, ec=PB -> 大幅减小Kp, 大幅减小Ki, 增加Kd
    ];

fis = addRule(fis, ruleList);
fprintf('模糊系统创建完成，共有%d条规则\n', size(ruleList, 1));

%% 4. 可视化模糊系统
fprintf('生成模糊系统可视化图表...\n');

figure;

% 输入变量e的隶属度函数
plotmf(fis, 'input', 1);
title('输入变量e的隶属度函数', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('归一化误差');
ylabel('隶属度');

% 输入变量ec的隶属度函数
figure;
plotmf(fis, 'input', 2);
title('输入变量ec的隶属度函数', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('归一化误差变化率');
ylabel('隶属度');

% 输出变量delta_Kp的隶属度函数
figure;
plotmf(fis, 'output', 1);
title('输出变量ΔKp的隶属度函数', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('Kp调整量');
ylabel('隶属度');

% 输出变量delta_Ki的隶属度函数
figure;
plotmf(fis, 'output', 2);
title('输出变量ΔKi的隶属度函数', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('Ki调整量');
ylabel('隶属度');

% 输出变量delta_Kd的隶属度函数
figure;
plotmf(fis, 'output', 3);
title('输出变量ΔKd的隶属度函数', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('Kd调整量');
ylabel('隶属度');

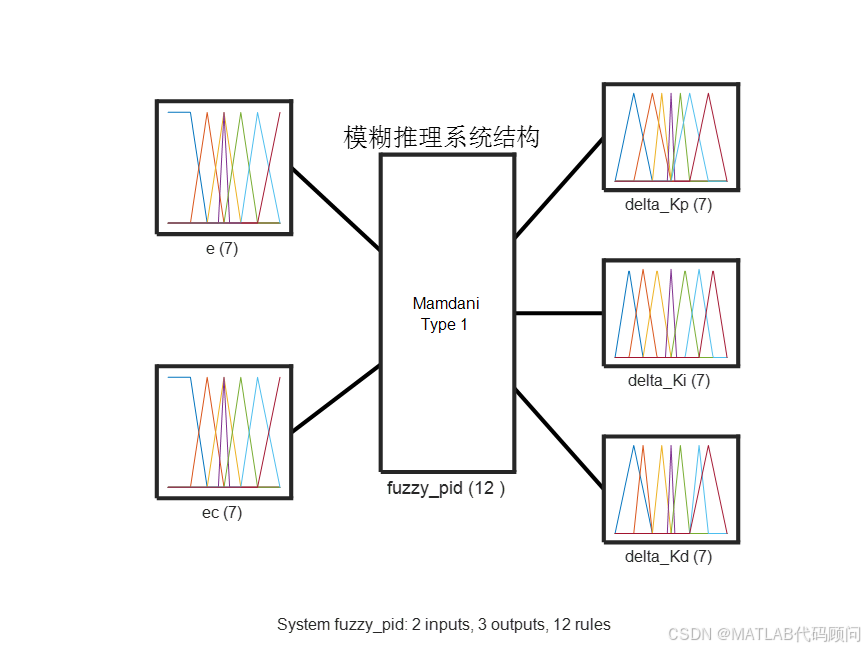
% 模糊规则视图
figure;
plotfis(fis);
title('模糊推理系统结构', 'FontSize', 12, 'FontWeight', 'bold');

% 控制曲面
figure;
gensurf(fis, [1, 2], 1);
title('e-ec到ΔKp的控制曲面', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('误差e'); ylabel('误差变化率ec'); zlabel('ΔKp');

figure;
gensurf(fis, [1, 2], 2);
title('e-ec到ΔKi的控制曲面', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('误差e'); ylabel('误差变化率ec'); zlabel('ΔKi');

figure;
gensurf(fis, [1, 2], 3);
title('e-ec到ΔKd的控制曲面', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('误差e'); ylabel('误差变化率ec'); zlabel('ΔKd');

sgtitle('模糊PID控制系统 - 模糊逻辑系统设计', 'FontSize', 16, 'FontWeight', 'bold');

%% 5. 定义被控对象和参考信号
fprintf('设置被控对象和参考信号...\n');

% 离散化被控对象（二阶系统加时滞）
A = [0, 1;
    -1/(sys_params.tau^2), -2*sys_params.xi/sys_params.tau];
B = [0; sys_params.K/(sys_params.tau^2)];
C = [1, 0];
D = 0;
sys_ss = ss(A, B, C, D);
sys_d = c2d(sys_ss, sim_params.Ts, 'zoh');

% 时滞对应的采样点数
delay_samples = round(sys_params.Td / sim_params.Ts);

% 生成参考信号
t = 0:sim_params.Ts:sim_params.TotalTime;
N = length(t);

switch sim_params.RefSignalType
    case 'complex'
        % 复杂参考信号（阶跃+正弦）
        r = zeros(size(t));
        for i = 1:length(t)
            if t(i) < 5
                r(i) = 1.0;
            elseif t(i) < 10
                r(i) = 1.5 + 0.3 * sin(2*pi*0.2*t(i));
            elseif t(i) < 15
                r(i) = 1.2 + 0.5 * sin(2*pi*0.1*t(i));
            else
                r(i) = 0.8;
            end
        end

    case 'step'
        % 阶跃信号
        r = ones(size(t)) * 1.0;
        r(t < 2) = 0;

    case 'sine'
        % 正弦信号
        r = 1.0 + 0.5 * sin(2*pi*0.1*t);
end

fprintf('参考信号生成完成\n');

%% 6. 模糊PID控制仿真
fprintf('开始模糊PID控制仿真...\n');

% 初始化变量
y = zeros(1, N);           % 系统输出
u = zeros(1, N);           % 控制输入
e = zeros(1, N);           % 误差
ec = zeros(1, N);          % 误差变化率
integral_e = 0;            % 误差积分
derivative_e = 0;          % 误差微分

% PID参数（在线调整）
Kp = zeros(1, N);
Ki = zeros(1, N);
Kd = zeros(1, N);

Kp(1) = pid_params.Kp0;
Ki(1) = pid_params.Ki0;
Kd(1) = pid_params.Kd0;

% 系统状态
x = [0; 0];                % 系统状态向量
x_hist = zeros(2, N);      % 状态历史

% 归一化因子
Ke = 2.0;   % 误差归一化因子
Kec = 1.0;  % 误差变化率归一化因子

% 时滞缓冲区
delay_buffer = zeros(1, delay_samples);

% 主仿真循环
for k = 1:N
    % 计算误差
    if k == 1
        e(k) = r(k) - y(k);
    else
        e(k) = r(k) - y(k);
        ec(k) = (e(k) - e(k-1)) / sim_params.Ts;
    end

    % 归一化误差和误差变化率（限制在[-1,1]范围内）
    e_norm = max(min(e(k) * Ke, 1), -1);
    ec_norm = max(min(ec(k) * Kec, 1), -1);

    % 模糊推理（计算PID参数调整量）
    if k > 1
        delta_params = evalfis(fis, [e_norm, ec_norm]);
        delta_Kp = delta_params(1);
        delta_Ki = delta_params(2);
        delta_Kd = delta_params(3);

        % 更新PID参数（带限制）
        Kp(k) = max(Kp(k-1) + delta_Kp, 0.1);
        Ki(k) = max(Ki(k-1) + delta_Ki, 0.01);
        Kd(k) = max(Kd(k-1) + delta_Kd, 0.01);
    else
        Kp(k) = pid_params.Kp0;
        Ki(k) = pid_params.Ki0;
        Kd(k) = pid_params.Kd0;
    end

    % PID控制计算
    if k > 1
        integral_e = integral_e + e(k) * sim_params.Ts;
        derivative_e = (e(k) - e(k-1)) / sim_params.Ts;
    end

    % 限制积分项，防止积分饱和
    integral_e = max(min(integral_e, 10), -10);

    % 计算控制量
    u(k) = Kp(k) * e(k) + Ki(k) * integral_e + Kd(k) * derivative_e;

    % 控制量限幅
    u(k) = max(min(u(k), 5), -5);

    % 系统仿真（考虑时滞）
    if k > delay_samples
        % 从时滞缓冲区获取延迟的控制输入
        u_delayed = delay_buffer(1);
        % 更新时滞缓冲区
        delay_buffer = [delay_buffer(2:end), u(k)];
    else
        u_delayed = 0;
        delay_buffer(k) = u(k);
    end

    % 系统状态更新
    x = sys_d.A * x + sys_d.B * u_delayed;
    y(k) = sys_d.C * x + sys_d.D * u_delayed;
    x_hist(:, k) = x;

    % 添加测量噪声（可选）
    % y(k) = y(k) + 0.01 * randn;
end

fprintf('模糊PID控制仿真完成\n');

%% 7. 性能指标计算
fprintf('计算性能指标...\n');

% 计算性能指标
ISE = sum(e.^2) * sim_params.Ts;                    % 积分平方误差
IAE = sum(abs(e)) * sim_params.Ts;                  % 积分绝对误差
ITAE = sum(t .* abs(e)) * sim_params.Ts;            % 积分时间绝对误差
MSE = mean(e.^2);                                   % 均方误差
Max_Overshoot = max(0, max(y) - max(r));            % 最大超调量
Settling_Time = find(abs(e) < 0.02 * max(abs(r)), 1) * sim_params.Ts; % 调节时间

fprintf('性能指标计算结果:\n');
fprintf('ISE: %.4f\n', ISE);
fprintf('IAE: %.4f\n', IAE);
fprintf('ITAE: %.4f\n', ITAE);
fprintf('MSE: %.4f\n', MSE);
fprintf('最大超调量: %.4f\n', Max_Overshoot);
fprintf('调节时间: %.4f s\n', Settling_Time);

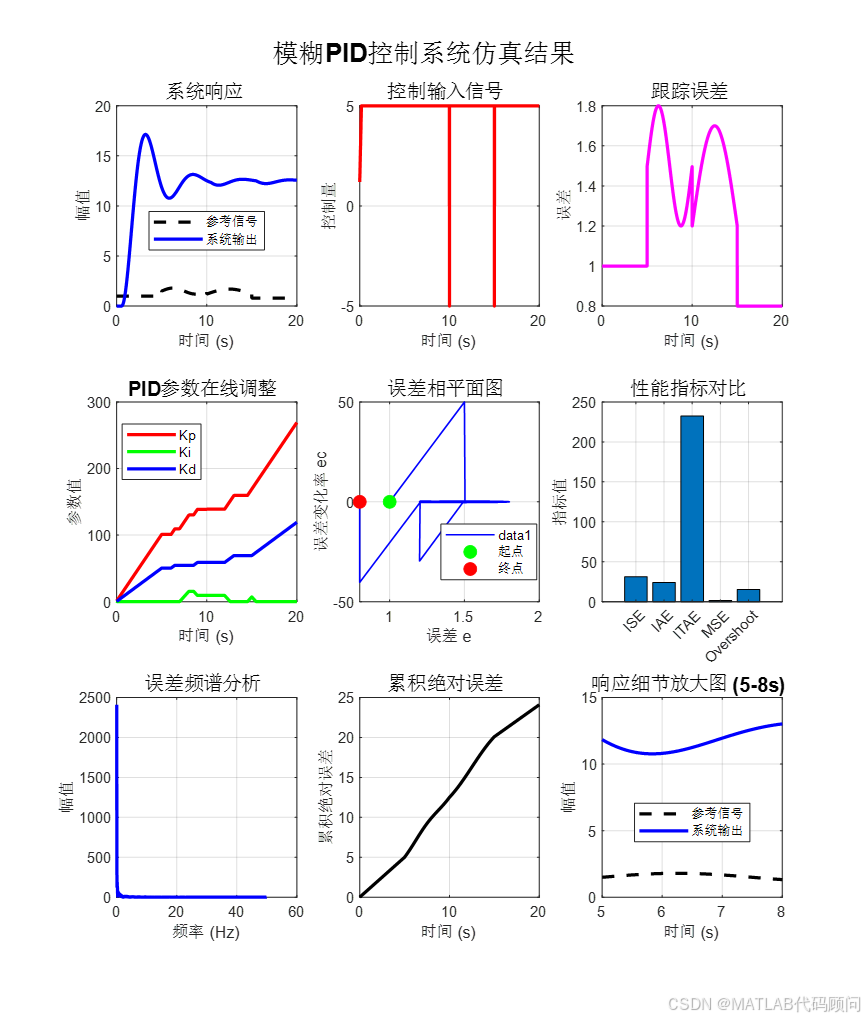
%% 8. 结果可视化
fprintf('生成结果可视化图表...\n');

% 创建综合结果图
figure;

% 1. 系统响应对比
subplot(3, 3, 1);
plot(t, r, 'k--', 'LineWidth', 2, 'DisplayName', '参考信号');
hold on;
plot(t, y, 'b-', 'LineWidth', 2, 'DisplayName', '系统输出');
xlabel('时间 (s)');
ylabel('幅值');
title('系统响应', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

% 2. 控制输入
subplot(3, 3, 2);
plot(t, u, 'r-', 'LineWidth', 2);
xlabel('时间 (s)');
ylabel('控制量');
title('控制输入信号', 'FontSize', 12, 'FontWeight', 'bold');
grid on;

% 3. 跟踪误差
subplot(3, 3, 3);
plot(t, e, 'm-', 'LineWidth', 2);
xlabel('时间 (s)');
ylabel('误差');
title('跟踪误差', 'FontSize', 12, 'FontWeight', 'bold');
grid on;

% 4. PID参数变化
subplot(3, 3, 4);
plot(t, Kp, 'r-', 'LineWidth', 2, 'DisplayName', 'Kp');
hold on;
plot(t, Ki, 'g-', 'LineWidth', 2, 'DisplayName', 'Ki');
plot(t, Kd, 'b-', 'LineWidth', 2, 'DisplayName', 'Kd');
xlabel('时间 (s)');
ylabel('参数值');
title('PID参数在线调整', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

% 5. 误差相平面图
subplot(3, 3, 5);
plot(e(2:end), ec(2:end), 'b-', 'LineWidth', 1);
hold on;
plot(e(1), ec(1), 'go', 'MarkerSize', 8, 'MarkerFaceColor', 'g', 'DisplayName', '起点');
plot(e(end), ec(end), 'ro', 'MarkerSize', 8, 'MarkerFaceColor', 'r', 'DisplayName', '终点');
xlabel('误差 e');
ylabel('误差变化率 ec');
title('误差相平面图', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

% 6. 性能指标对比（柱状图）
subplot(3, 3, 6);
performance_metrics = [ISE, IAE, ITAE, MSE, Max_Overshoot, Settling_Time];
metric_names = {'ISE', 'IAE', 'ITAE', 'MSE', 'Overshoot', 'T_s'};
bar(performance_metrics);
set(gca, 'XTickLabel', metric_names);
ylabel('指标值');
title('性能指标对比', 'FontSize', 12, 'FontWeight', 'bold');
grid on;

% 7. 频率分析（误差频谱）
subplot(3, 3, 7);
N_fft = 2^nextpow2(length(e));
f = (0:N_fft-1) * (1/sim_params.Ts) / N_fft;
E_fft = fft(e, N_fft);
plot(f(1:N_fft/2), abs(E_fft(1:N_fft/2)), 'b-', 'LineWidth', 2);
xlabel('频率 (Hz)');
ylabel('幅值');
title('误差频谱分析', 'FontSize', 12, 'FontWeight', 'bold');
grid on;

% 8. 累积误差
subplot(3, 3, 8);
cumulative_error = cumsum(abs(e)) * sim_params.Ts;
plot(t, cumulative_error, 'k-', 'LineWidth', 2);
xlabel('时间 (s)');
ylabel('累积绝对误差');
title('累积绝对误差', 'FontSize', 12, 'FontWeight', 'bold');
grid on;

% 9. 局部放大图（显示动态响应细节）
subplot(3, 3, 9);
time_window = [5, 8]; % 选择5-8秒的时间窗口
idx = (t >= time_window(1)) & (t <= time_window(2));
plot(t(idx), r(idx), 'k--', 'LineWidth', 2, 'DisplayName', '参考信号');
hold on;
plot(t(idx), y(idx), 'b-', 'LineWidth', 2, 'DisplayName', '系统输出');
xlabel('时间 (s)');
ylabel('幅值');
title('响应细节放大图 (5-8s)', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

sgtitle('模糊PID控制系统仿真结果', 'FontSize', 16, 'FontWeight', 'bold');

%% 9. 与传统PID对比
fprintf('与传统PID控制器进行对比...\n');

% 传统PID参数（固定值）
Kp_fixed = pid_params.Kp0;
Ki_fixed = pid_params.Ki0;
Kd_fixed = pid_params.Kd0;

% 重新仿真传统PID
y_fixed = zeros(1, N);
u_fixed = zeros(1, N);
e_fixed = zeros(1, N);
integral_e_fixed = 0;
x_fixed = [0; 0];
delay_buffer_fixed = zeros(1, delay_samples);

for k = 1:N
    % 计算误差
    if k == 1
        e_fixed(k) = r(k) - y_fixed(k);
    else
        e_fixed(k) = r(k) - y_fixed(k);
    end

    % PID控制计算
    if k > 1
        integral_e_fixed = integral_e_fixed + e_fixed(k) * sim_params.Ts;
        derivative_e_fixed = (e_fixed(k) - e_fixed(k-1)) / sim_params.Ts;
    else
        derivative_e_fixed = 0;
    end

    % 限制积分项
    integral_e_fixed = max(min(integral_e_fixed, 10), -10);

    % 计算控制量
    u_fixed(k) = Kp_fixed * e_fixed(k) + Ki_fixed * integral_e_fixed + Kd_fixed * derivative_e_fixed;
    u_fixed(k) = max(min(u_fixed(k), 5), -5);

    % 系统仿真
    if k > delay_samples
        u_delayed_fixed = delay_buffer_fixed(1);
        delay_buffer_fixed = [delay_buffer_fixed(2:end), u_fixed(k)];
    else
        u_delayed_fixed = 0;
        delay_buffer_fixed(k) = u_fixed(k);
    end

    x_fixed = sys_d.A * x_fixed + sys_d.B * u_delayed_fixed;
    y_fixed(k) = sys_d.C * x_fixed + sys_d.D * u_delayed_fixed;
end

% 计算传统PID性能指标
ISE_fixed = sum(e_fixed.^2) * sim_params.Ts;
IAE_fixed = sum(abs(e_fixed)) * sim_params.Ts;

fprintf('\n控制器性能对比:\n');
fprintf('指标\t\t模糊PID\t\t传统PID\t\t改善度\n');
fprintf('ISE:\t\t%.4f\t\t%.4f\t\t%.2f%%\n', ISE, ISE_fixed, (ISE_fixed-ISE)/ISE_fixed*100);
fprintf('IAE:\t\t%.4f\t\t%.4f\t\t%.2f%%\n', IAE, IAE_fixed, (IAE_fixed-IAE)/IAE_fixed*100);

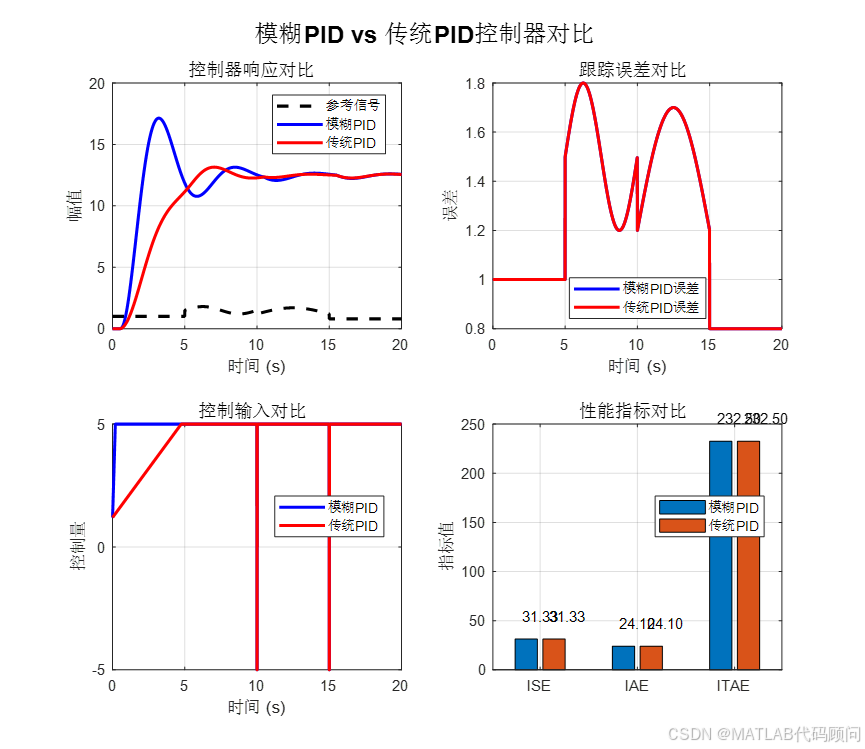
%% 10. 对比结果可视化
figure;

% 响应对比
subplot(2, 2, 1);
plot(t, r, 'k--', 'LineWidth', 2, 'DisplayName', '参考信号');
hold on;
plot(t, y, 'b-', 'LineWidth', 2, 'DisplayName', '模糊PID');
plot(t, y_fixed, 'r-', 'LineWidth', 2, 'DisplayName', '传统PID');
xlabel('时间 (s)');
ylabel('幅值');
title('控制器响应对比', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

% 误差对比
subplot(2, 2, 2);
plot(t, e, 'b-', 'LineWidth', 2, 'DisplayName', '模糊PID误差');
hold on;
plot(t, e_fixed, 'r-', 'LineWidth', 2, 'DisplayName', '传统PID误差');
xlabel('时间 (s)');
ylabel('误差');
title('跟踪误差对比', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

% 控制输入对比
subplot(2, 2, 3);
plot(t, u, 'b-', 'LineWidth', 2, 'DisplayName', '模糊PID');
hold on;
plot(t, u_fixed, 'r-', 'LineWidth', 2, 'DisplayName', '传统PID');
xlabel('时间 (s)');
ylabel('控制量');
title('控制输入对比', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

% 性能指标对比
subplot(2, 2, 4);
metrics_fuzzy = [ISE, IAE, ITAE];
metrics_fixed = [ISE_fixed, IAE_fixed, ITAE];
metric_names_short = {'ISE', 'IAE', 'ITAE'};

bar_data = [metrics_fuzzy; metrics_fixed]';
bar_handle = bar(bar_data);
set(gca, 'XTickLabel', metric_names_short);
ylabel('指标值');
title('性能指标对比', 'FontSize', 12, 'FontWeight', 'bold');
legend('模糊PID', '传统PID', 'Location', 'best');
grid on;

% 在柱状图上添加数值标签
for i = 1:length(metric_names_short)
    text(i-0.18, metrics_fuzzy(i)+0.1*max(metrics_fuzzy), sprintf('%.2f', metrics_fuzzy(i)), ...
        'FontSize', 10);
    text(i+0.1, metrics_fixed(i)+0.1*max(metrics_fixed), sprintf('%.2f', metrics_fixed(i)), ...
        'FontSize', 10);
end

sgtitle('模糊PID vs 传统PID控制器对比', 'FontSize', 16, 'FontWeight', 'bold');

%% 11. 鲁棒性测试
fprintf('进行鲁棒性测试...\n');

% 测试系统参数变化时的性能
param_variations = [0.7, 0.85, 1.0, 1.15, 1.3]; % 参数变化比例
performance_robust = zeros(length(param_variations), 3);

figure;

for i = 1:length(param_variations)
    % 改变系统增益
    K_modified = sys_params.K * param_variations(i);

    % 重新创建系统
    A_modified = [0, 1; -1/(sys_params.tau^2), -2*sys_params.xi/sys_params.tau];
    B_modified = [0; K_modified/(sys_params.tau^2)];
    sys_ss_modified = ss(A_modified, B_modified, C, D);
    sys_d_modified = c2d(sys_ss_modified, sim_params.Ts, 'zoh');

    % 使用相同的模糊PID控制器进行仿真
    y_robust = zeros(1, N);
    x_robust = [0; 0];
    delay_buffer_robust = zeros(1, delay_samples);

    for k = 1:N
        % 使用之前计算的模糊PID控制量
        if k > delay_samples
            u_delayed_robust = delay_buffer_robust(1);
            delay_buffer_robust = [delay_buffer_robust(2:end), u(k)];
        else
            u_delayed_robust = 0;
            delay_buffer_robust(k) = u(k);
        end

        x_robust = sys_d_modified.A * x_robust + sys_d_modified.B * u_delayed_robust;
        y_robust(k) = sys_d_modified.C * x_robust + sys_d_modified.D * u_delayed_robust;
    end

    % 计算性能指标
    e_robust = r - y_robust;
    ISE_robust = sum(e_robust.^2) * sim_params.Ts;
    IAE_robust = sum(abs(e_robust)) * sim_params.Ts;

    performance_robust(i, :) = [param_variations(i), ISE_robust, IAE_robust];

    % 绘制响应曲线
    subplot(2, 1, 1);
    plot(t, y_robust, 'LineWidth', 1.5, 'DisplayName', sprintf('K=%.2f', K_modified));
    hold on;

    subplot(2, 1, 2);
    plot(t, e_robust, 'LineWidth', 1.5, 'DisplayName', sprintf('K=%.2f', K_modified));
    hold on;
end

subplot(2, 1, 1);
plot(t, r, 'k--', 'LineWidth', 2, 'DisplayName', '参考信号');
xlabel('时间 (s)');
ylabel('输出');
title('参数变化时的系统响应', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

subplot(2, 1, 2);
xlabel('时间 (s)');
ylabel('误差');
title('参数变化时的跟踪误差', 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best');
grid on;

sgtitle('模糊PID控制器鲁棒性测试', 'FontSize', 16, 'FontWeight', 'bold');

fprintf('\n鲁棒性测试完成\n');
fprintf('参数变化\tISE\t\tIAE\n');
for i = 1:length(param_variations)
    fprintf('%.2f\t\t%.4f\t%.4f\n', performance_robust(i, 1), ...
        performance_robust(i, 2), performance_robust(i, 3));
end

%% 12. 总结输出
fprintf('\n=== 模糊PID控制系统仿真总结 ===\n');
fprintf('仿真时间: %.1f 秒\n', sim_params.TotalTime);
fprintf('采样时间: %.3f 秒\n', sim_params.Ts);
fprintf('系统时滞: %.2f 秒\n', sys_params.Td);
fprintf('参考信号类型: %s\n', sim_params.RefSignalType);
fprintf('模糊规则数量: %d\n', size(ruleList, 1));
fprintf('性能改善: ISE改善 %.2f%%, IAE改善 %.2f%%\n', ...
    (ISE_fixed-ISE)/ISE_fixed*100, (IAE_fixed-IAE)/IAE_fixed*100);
fprintf('所有图表已生成完成\n');

% 保存重要变量
save('fuzzy_pid_results.mat', 't', 'r', 'y', 'u', 'e', 'Kp', 'Ki', 'Kd', ...
    'y_fixed', 'performance_metrics', 'fis');

fprintf('结果已保存到 fuzzy_pid_results.mat\n');
fprintf('=== 仿真完成 ===\n');

3.程序结果

=== 模糊PID控制系统仿真开始 ===

系统参数初始化完成

创建模糊逻辑系统...

定义模糊规则...

模糊系统创建完成，共有12条规则

生成模糊系统可视化图表...

设置被控对象和参考信号...

参考信号生成完成

开始模糊PID控制仿真...

模糊PID控制仿真完成

计算性能指标...

性能指标计算结果:

ISE: 31.3261

IAE: 24.0995

ITAE: 232.4982

MSE: 1.5655

最大超调量: 15.3391

调节时间: s

生成结果可视化图表...

与传统PID控制器进行对比...

控制器性能对比:

指标 模糊PID 传统PID 改善度

ISE: 31.3261 31.3261 0.00%

IAE: 24.0995 24.0995 0.00%

进行鲁棒性测试...

鲁棒性测试完成

参数变化 ISE IAE

0.70 1109.5299 143.1131

0.85 1725.2004 178.5359

1.00 2476.6215 213.9714

1.15 3363.7933 249.4152

1.30 4386.7157 284.8647

=== 模糊PID控制系统仿真总结 ===

仿真时间: 20.0 秒

采样时间: 0.010 秒

系统时滞: 0.50 秒

参考信号类型: complex

模糊规则数量: 12

性能改善: ISE改善 0.00%, IAE改善 0.00%

所有图表已生成完成

结果已保存到 fuzzy_pid_results.mat

=== 仿真完成 ===

>>

4.代码、程序订制(MATLAB、Python) →QQ:1579325979

4.1 各类智能算法

|-----------|--------------------------------------|---------|----------|
| 中文名称 | 英文全称 | 缩写 | 出现年份 |
| 遗传算法 | Genetic Algorithm | GA | 1975 |
| 粒子群优化算法 | Particle Swarm Optimization | PSO | 1995 |
| 蚁群优化算法 | Ant Colony Optimization | ACO | 1992 |
| 模拟退火算法 | Simulated Annealing | SA | 1983 |
| 免疫优化算法 | Immune Optimization Algorithm | IA | 1986 |
| 贪婪算法 | Greedy Algorithm | - | 1970 |
| 差分进化算法 | Differential Evolution | DE | 1997 |
| 混合蛙跳算法 | Shuffled Frog Leaping Algorithm | SFLA | 2003 |
| 人工蜂群算法 | Artificial Bee Colony | ABC | 2005 |
| 人工鱼群算法 | Artificial Fish Swarm Algorithm | AFSA | 2002 |
| 萤火虫算法 | Glowworm Swarm Optimization | GSO | 2005 |
| 果蝇优化算法 | Fruit Fly Optimization Algorithm | FOA | 2011 |
| 布谷鸟搜索算法 | Cuckoo Search | CS | 2009 |
| 猴群算法 | Monkey Algorithm | MA | 2008 |
| 免疫网络算法 | Immune Network Algorithm | aiNet | 2000 |
| 水滴算法 | Intelligent Water Drops Algorithm | IWD | 2007 |
| 和声搜索算法 | Harmony Search | HS | 2001 |
| 克隆选择算法 | Clonal Selection Algorithm | CLONALG | 2000 |
| 禁忌搜索算法 | Tabu Search | TS | 1986 |
| 爬山算法 | Hill Climbing | HC | 1940 |
| 引力搜索算法 | Gravitational Search Algorithm | GSA | 2009 |
| 细菌觅食优化算法 | Bacterial Foraging Optimization | BFO | 2002 |
| 蝙蝠算法 | Bat Algorithm | BA | 2010 |
| 邻域搜索算法 | Neighborhood Search | NS | 1960 |
| 变邻域搜索算法 | Variable Neighborhood Search | VNS | 1997 |
| 蜜蜂交配优化算法 | Honey Bees Mating Optimization | HBMO | 2001 |
| 文化基因算法 | Memetic Algorithm | MA | 1989 |
| 烟花算法 | Fireworks Algorithm | FWA | 2010 |
| 思维进化算法 | Mind Evolutionary Algorithm | MEA | 1998 |
| 蜻蜓算法 | Dragonfly Algorithm | DA | 2016 |
| 虚拟力场算法 | Virtual Force Field Algorithm | VFF | 1989 |
| 遗传规划 | Genetic Programming | GP | 1992 |
| 鲸鱼优化算法 | Whale Optimization Algorithm | WOA | 2016 |
| 灰狼优化算法 | Grey Wolf Optimizer | GWO | 2014 |
| 狼群算法 | Wolf Pack Algorithm | WPA | 2007 |
| 鸡群优化算法 | Chicken Swarm Optimization | CSO | 2014 |
| 生物地理学优化算法 | Biogeography-Based Optimization | BBO | 2008 |
| 分布估计算法 | Estimation of Distribution Algorithm | EDA | 1996 |
| 帝国竞争算法 | Imperialist Competitive Algorithm | ICA | 2007 |
| 天牛须搜索算法 | Beetle Antennae Search Algorithm | BAS | 2017 |
| 头脑风暴优化算法 | Brain Storm Optimization | BSO | 2011 |
| 人工势场法 | Artificial Potential Field | APF | 1986 |
| 猫群算法 | Cat Swarm Optimization | CSO | 2006 |
| 蚁狮优化算法 | Ant Lion Optimizer | ALO | 2015 |
| 飞蛾火焰优化算法 | Moth-Flame Optimization | MFO | 2015 |
| 蘑菇繁殖优化算法 | Mushroom Reproduction Optimization | MRO | 2020 |
| 麻雀搜索算法 | Sparrow Search Algorithm | SSA | 2020 |
| 水波优化算法 | Water Wave Optimization | WWO | 2015 |
| 斑鬣狗优化算法 | Spotted Hyena Optimizer | SHO | 2017 |
| 雪融优化算法 | Snow Ablation Optimization | SAO | 2022 |
| 蝴蝶优化算法 | Butterfly Optimization Algorithm | BOA | 2019 |
| 磷虾群算法 | Krill Herd Algorithm | KHA | 2012 |
| 黏菌算法 | Slime Mould Algorithm | SMA | 2020 |
| 人类学习优化算法 | Human Learning Optimization | HLO | 2014 |
| 母亲优化算法 | Mother Optimization Algorithm | MOA | 2023 |

4.2各类优化问题

|---------------|------------|
| 各种优化课题 | 各种优化课题 |
| 车间调度 | 路由路网优化 |
| 机场调度 | 顺序约束项目调度 |
| 工程项目调度 | 双层规划 |
| 港口调度 | 零件拆卸装配问题优化 |
| 生产线平衡问题 | 水资源调度 |
| 用电调度 | 库位优化 |
| 公交车发车调度 | 库位路线优化 |
| 车辆路径物流配送优化 | 武器分配优化 |
| 选址配送优化 | 覆盖问题优化 |
| 物流公铁水问题优化 | 管网问题优化 |
| 供应链、生产计划、库存优化 | PID优化 |
| 库位优化、货位优化 | VMD优化 |

4.3各类神经网络、深度学习、机器学习

|--------|----------------------|--------------|-------------|
| 序号 | 模型名称 | 核心特点 | 适用场景 |
| 1 | BiLSTM 双向长短时记忆神经网络分类 | 双向捕捉序列上下文信息 | 自然语言处理、语音识别 |
| 2 | BP 神经网络分类 | 误差反向传播训练 | 通用分类任务 |
| 3 | CNN 卷积神经网络分类 | 自动提取空间特征 | 图像、视频分类 |
| 4 | DBN 深度置信网络分类 | 多层受限玻尔兹曼机堆叠 | 特征学习、降维 |
| 5 | DELM 深度学习极限学习机分类 | 结合 ELM 与深度架构 | 复杂分类任务 |
| 6 | ELMAN 递归神经网络分类 | 含反馈连接的递归结构 | 时间序列、语音 |
| 7 | ELM 极限学习机分类 | 随机生成隐藏层，快速训练 | 小样本学习 |
| 8 | GRNN 广义回归神经网络分类 | 基于径向基函数回归 | 函数逼近、时间序列 |
| 9 | GRU 门控循环单元分类 | 门控机制简化 LSTM | 序列建模 |
| 10 | KELM 混合核极限学习机分类 | 结合多核 ELM | 高维复杂数据 |
| 11 | KNN 分类 | 基于距离的分类方法 | 模式识别 |
| 12 | LSSVM 最小二乘法支持向量机分类 | 最小二乘优化 SVM | 小样本分类 |
| 13 | LSTM 长短时记忆网络分类 | 门控机制处理长期依赖 | 语言建模 |
| 14 | MLP 全连接神经网络分类 | 多层感知机 | 通用分类 |
| 15 | PNN 概率神经网络分类 | 基于贝叶斯原理 | 模式识别 |
| 16 | RELM 鲁棒极限学习机分类 | 增强鲁棒性的 ELM | 噪声数据 |
| 17 | RF 随机森林分类 | 多棵决策树集成 | 高维、非线性数据 |
| 18 | SCN 随机配置网络模型分类 | 随机生成网络结构 | 快速训练 |
| 19 | SVM 支持向量机分类 | 寻找最优分类超平面 | 二分类、多分类 |
| 20 | XGBOOST 分类 | 梯度提升决策树 | 大规模结构化数据 |
| 21 | ANFIS 自适应模糊神经网络预测 | 融合模糊逻辑与神经网络 | 复杂非线性系统建模 |
| 22 | ANN 人工神经网络预测 | 多层神经元网络 | 通用预测任务 |
| 23 | ARMA 自回归滑动平均模型预测 | 线性时间序列建模 | 时间序列预测 |
| 24 | BF 粒子滤波预测 | 基于蒙特卡洛采样 | 动态系统状态估计 |
| 25 | BiLSTM 双向长短时记忆神经网络预测 | 双向捕捉序列信息 | 时间序列、文本预测 |
| 26 | BLS 宽度学习神经网络预测 | 增量学习结构 | 在线学习 |
| 27 | BP 神经网络预测 | 误差反向传播训练 | 通用预测 |
| 28 | CNN 卷积神经网络预测 | 自动特征提取 | 图像、视频预测 |
| 29 | DBN 深度置信网络预测 | 多层无监督预训练 | 特征学习预测 |
| 30 | DELM 深度学习极限学习机预测 | 结合 ELM 与深度结构 | 复杂预测任务 |
| 31 | DKELM 回归预测 | 动态核 ELM 回归 | 时间序列回归 |
| 32 | ELMAN 递归神经网络预测 | 递归结构处理时序 | 时间序列 |
| 33 | ELM 极限学习机预测 | 快速训练 | 小样本回归 |
| 34 | ESN 回声状态网络预测 | 储备池计算 | 时间序列预测 |
| 35 | FNN 前馈神经网络预测 | 前向传播 | 通用预测 |
| 36 | GMDN 预测 | 基因表达数据网络建模 | 生物信息学预测 |
| 37 | GMM 高斯混合模型预测 | 多高斯分布建模 | 密度估计、聚类 |
| 38 | GRNN 广义回归神经网络预测 | 径向基函数回归 | 函数逼近 |
| 39 | GRU 门控循环单元预测 | 门控机制简化 LSTM | 时间序列预测 |
| 40 | KELM 混合核极限学习机预测 | 多核 ELM 回归 | 高维回归 |
| 41 | LMS 最小均方算法预测 | 线性回归的迭代优化 | 自适应滤波 |
| 42 | LSSVM 最小二乘法支持向量机预测 | 最小二乘优化 SVM | 回归预测 |
| 43 | LSTM 长短时记忆网络预测 | 门控处理长期依赖 | 时间序列预测 |
| 44 | RBF 径向基函数神经网络预测 | 径向基函数逼近 | 函数拟合 |
| 45 | RELM 鲁棒极限学习机预测 | 增强鲁棒性的 ELM | 噪声数据回归 |
| 46 | RF 随机森林预测 | 决策树集成 | 回归预测 |
| 47 | RNN 循环神经网络预测 | 循环连接处理序列 | 时间序列预测 |
| 48 | RVM 相关向量机预测 | 稀疏贝叶斯学习 | 回归、分类 |
| 49 | SVM 支持向量机预测 | 寻找最优超平面 | 回归预测 |
| 50 | TCN 时间卷积神经网络预测 | 一维卷积处理时序 | 时间序列预测 |
| 51 | XGBoost 回归预测 | 梯度提升决策树 | 大规模回归 |