023数据结构之线段树——算法备赛

线段树

线段树（Segment Tree）可以说是竞赛出题人最喜欢考核的数据结构了。线段树是历程碑式的知识点，熟练掌握线段树，标志着脱离初级学习阶段，走向中高级学习阶段------《算法竞赛》。

基本应用场景

下面举例基本应用场景：

区间最值问题

有长度为 n 的数组 a ，需多次进行一下操作

求最值，对于原数组，给定i,j≤n，求区间[i,j]内的最值
修改元素，对于原数组a，给定 k 和 x，把第 k个元素 a[k]修改为x

如果用普通数组存储，上述两个操作，单次求最值的复杂度为O(n)，修改元素的复杂度为O(1)。如果有m次修改元素+求最值操作，总复杂度就是O(mn)。如果 m 和 n 比较大，那这个复杂度在竞赛中是不可接受的。

区间和问题

给出一个长度为 n 的数组 a ，先更改某些数的值，然后询问给定 i,j≤n，求数组[i,j]区间和。更改和询问操作总数为m，总的复杂度就是O(mn)。

对于上述两类问题，线段树都可以在O(mlogn)的时间复杂度内解决。

线段树和树状数组都是解决区间问题的数据结构。他们各有优点。

逻辑结构。线段树基于二叉树，数据结构直观，清晰易懂。另外，由于二叉树灵活丰富，能用于更多场景，比树状数组适应面广。
代码长度。线段树的维护需要维护二叉树，而树状数组只需处理一个Tree数组，所以线段树的代码更长。

线段树概念

基本定义

概括的说，线段树可以理解为 分治+二叉树结构+Lazy-Tag技术 （针对区间修改问题的Lazy-Tag技术，后面高级部分再介绍）。

线段树是分治法 和二叉树的结合。它本质是一棵二叉树，树上的节点是==【线段】==（或者理解为区间），线段是根据分治法得到的。

图示为包含10个元素的线段树

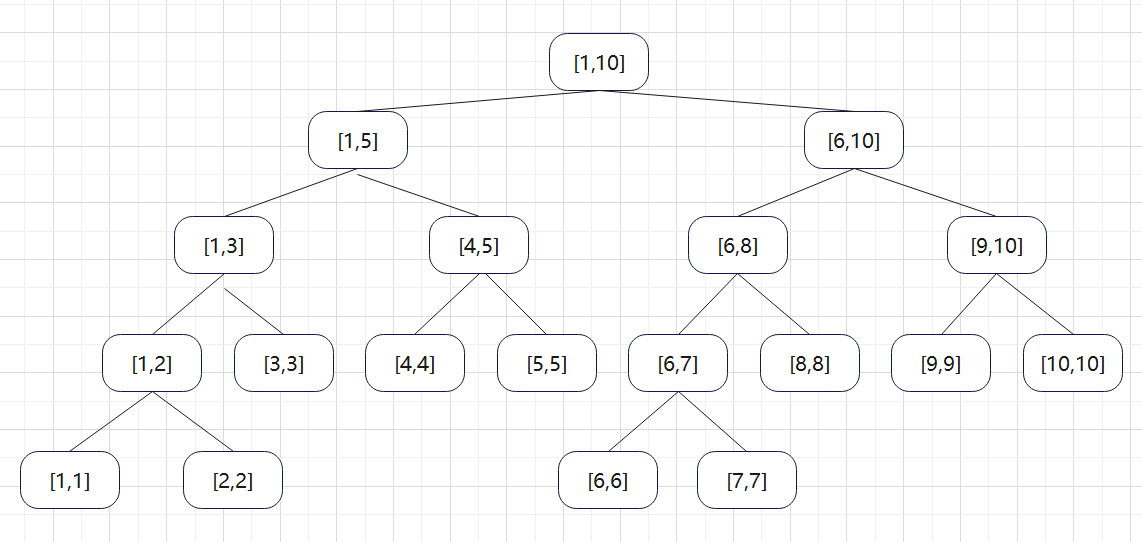
它的基本特征如下：

用分治法自顶而下建立，每次分治，左右子树各一半。
每个节点都表示一个线段区间，非叶子节点都包含多个元素，叶子节点只有一个元素。
除最后一层不一定满外，其他层都是满的。

考查每个线段[L,R]

L=R，说明这个节点只有一个元素，是一个叶子节点。
L<R，说明这个节点代表多个元素，它有两个孩子，左孩子 [L,M] ,右孩子 [M+1,R]，其中M=(L+R)/2。

节点所代表的值，可以是区间和，最值或其他灵活定义的值。

线段树的核心理念是大区间的解可以从小区间的解合并而来。

元素数量与节点数量的关系

了解了线段树的定义与结构，我们来探讨一下【原数组元素数量】与【线段树节点数量】的关系（这对后面封装数据结构有帮助）。

以上述10个元素的原数组 为例，它对应的线段树 节点数量有19个。

具体地，原数组大小为n，其对应的线段树的节点数量size是多少呢？

首先线段树的叶子节点数是n，因为线段树除最后一层不一定满外，其他层都是满的 ，所以最后一层【满节点的层数】为 ⌊log₂n⌋ (即n的二进制宽度bit_width(n)，记为s)，树的深度为 ⌈log₂n⌉ (即为bit_width(n-1)+1)。

剩余未满的一层节点数为2*(n-(1<<s-1))，总的节点数就是(1<<s-1) + 2*(n-(1<<s-1))。

在后续编码中，为了快速编写代码，常使用静态数组来实现一棵【满二叉树】，所以需要的空间最少为1<<(bit_width(n-1)+1)也可写成2<<bit_width(n-1)，粗放一点，可以开n<<2的空间。

定义数据结构

竞赛中一般使用静态数组来实现满二叉树

cpp 复制代码

//定义根节点为tree[1],tree[0]不用。
//第一种方法：定义二叉树结构体
struct{
    int L,R,data;
}tree[N<<2];  //分配静态数组，开4倍空间
//第二种方法：直接用数组表示二叉树，竞赛时常用。
int tree[N<<2];   //二叉树空间开4倍，即元素数量的4倍
int ls(int p){return p<<1;}  //p号节点的左孩子，下标为p*2
int rs(int p){return p<<1|1;}  //p号节点的右孩子，下标为p*2+1;  或写成 （p<<1）+1

构造线段树(以求区间和为例)

cpp 复制代码

void push_up(int p){
	tree[p]=tree[ls(p)]+tree[rs(p)];
    //tree[p]=max(tree[ls(p)],tree[rs(p)])  求最大值
}
void build(int p,int pl,int pr){  //节点p指向区间[pl,pr]
    if(pl==pr){tree[p]=a[pl];return;}  //递归出口，找到底层叶子节点，存值。
    int mid=(pl+pr)>>1;  //分治，折半
    build(ls(p),pl,mid);  //递归左孩子
    build(rs(p),mid+1,pr);  //递归右孩子
    push_up(p);  //回溯 从下往上传递区间和。
}  //调用  build(1,1,n) 完成初始化

区间查询(以查询区间和为例)

cpp 复制代码

//递归查询
int query(int L,int R,int p,int pl,int pr){
    if(L<=p1&&pr<=R) return tree[p];  //完全覆盖，直接返回
    int mid=(pl,pr)>>1;  //mid为p节点的左孩子的右边界  mid+1为p节点右孩子的左边界
    //res定义为全局变量
    if(L<=mid) res+=query(L,R,ls(p),p,mid);  //L与左子节点重叠。
    if(R>mid) res+=query(L,R,rs(p),mid+1,pr);  //R与右子节点重叠。
    return res;
}  //调用 query(L,R,1,1,n)  (L,R)为要查询的区间。

类模版封装(以区间最大值为例)

cpp 复制代码

class SegmentTree{  //以区间最大值为例
    vector<int>mx;
    void maintain(int i){
        mx[i]=max(mx[i<<1],mx[(i<<1)+1]);
    }
    void build(const vector<int>d,int i,int l,int r){
        if(l==r){
            mx[i]=d[l];
            return;
        }
        int mid=(l+r)/2;
        build(d,i<<1,l,mid);
        build(d,(i<<1)+1,mid+1,r);
        maintain(i);
    }
public:
    SegmentTree(const vector<int>d){
		int n=d.size();
        mx.resize(2<<bit_width((unsigned)n-1));  //确定数组大小，节省空间
        build(d,1,0,n-1);
    }
    int findMax(int l,int r,int i,int L,int R){  //寻找区间[l,r]内最大值
        if(l<=L&&r>=R) return mx[i];
        int mid=(L+R)/2;
        int ls=INT_MIN,rs=INT_MAX;
        if(mid>=l) ls=findMax(l,r,i<<1,L,mid); //与左子树表示区间有重叠
        if(mid<r) rs=findMax(l,r,(i<<1)+1,mid+1,R);  //与右子树表示区间有重叠
        return max(ls,rs);
    }  //调用方式findMax(l,r,1,0,n-1); 
    int findFirstMax(int i,int l,int r,int x){  //寻找左数第一个大于等于x的数
        if(mx[i]<x) return -1;  //区间内没有大于等于x的数
        if(l==r) return l;  //寻找到叶子节点
        int mid=(l+r)/2;
        int ans=findFirstMax(i<<1,l,mid,x);  
        if(ans==-1) ans=findFirstMax((i<<1)+1,mid+1,r,x);  //左子树找不到再找右子树
        return ans;
    }
}

应用

龙骑士军团

问题描述

原题链接

思路解析

本题需要在[a,b]区间中选择一点 i 和[c,d]区间中选择一点 j，使区间[i,j]的区间和最大.

首先用计算以每个元素为右边界的前缀和sum。

进行q次查询，每次查询[c,d]区间的最大sum值和[a-1,b-1]区间的最小sum值。因为c>d所以两区间无交集，结果即为两者之差。

每次需要进行q次查询，考虑使用线段树数据结构，可在O(qlogn)的时间复杂度内完成。暴力法O(qn)将超时。

代码

cpp 复制代码

#include<algorithm>
#include<vector>
#include<iostream>
#include<climits>
#define ll long long
using namespace std;
int ls(int i) { return i << 1; }
int rs(int i) { return i << 1 | 1; }
struct node {
    ll Max, Min;
    node(ll a, ll b) { Max = a; Min = b; }
    node() { Max = 0, Min = 0; }
};
node tr = node(LONG_MIN, LONG_MAX);
vector<node>tree;
vector<ll>sum;
void init(int p, int l, int r) {
    if (l == r) { tree[p].Max = sum[l]; tree[p].Min = sum[l]; return; };
    int mid = (l + r) >> 1;
    init(ls(p), l, mid);
    init(rs(p), mid + 1, r);
    tree[p].Max = max(tree[ls(p)].Max, tree[rs(p)].Max);
    tree[p].Min = min(tree[ls(p)].Min, tree[rs(p)].Min);
}
node query(int L, int R, int p, int l, int r) {
    if (L <= l && R >= r) return tree[p];
    int mid = (l + r) >> 1;
    if (L <= mid) {  //目标区间与左子节点有重叠
        node st = query(L, R, ls(p), l, mid);
        tr.Max = max(tr.Max, st.Max);
        tr.Min = min(tr.Min, st.Min);
    }
    if (R > mid) {  //目标区间与右子节点有重叠
        node st = query(L, R, rs(p), mid + 1, r);
        tr.Max = max(tr.Max, st.Max);
        tr.Min = min(tr.Min, st.Min);
    }
    return tr;
}
int main()
{
    // 请在此输入您的代码
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n, q; cin >> n >> q;
    sum = vector<ll>(n + 1);
    tree = vector<node>(4 * n + 1);
    tree[0] = node();
    for (int i = 0; i < n; i++) {
        int arr;
        cin >> arr;
        sum[i + 1] = sum[i] + arr;
    }
    init(1, 1, n);
    while (q--) {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        ll min1, max2;
        //查询[a-1,b-1]中的最小值时，下标可能小于1，因此分情况讨论
        if (b == 1) min1 = 0;
        else if (a == 1)  min1 = min(0ll, query(1, b - 1, 1, 1, n).Min);
        else min1 = query(a - 1, b - 1, 1, 1, n).Min;
        tr = node(LONG_MIN, LONG_MAX);
        max2 = query(c, d, 1, 1, n).Max;
        tr = node(LONG_MIN, LONG_MAX);
        ll tar = max2 - min1;
        cout << tar;
        if (q > 0) cout << endl;
    }
    return 0;
}

水果成篮|||

问题描述

给你两个长度为 n 的整数数组，fruits 和 baskets，其中 fruits[i] 表示第 i 种水果的数量，baskets[j] 表示第 j 个篮子的容量。

你需要对 fruits 数组从左到右按照以下规则放置水果：

每种水果必须放入第一个 容量大于等于 该水果数量的 最左侧可用篮子 中。
每个篮子只能装一种水果。
如果一种水果 无法放入 任何篮子，它将保持 未放置。

返回所有可能分配完成后，剩余未放置的水果种类的数量。

原题链接

思路分析

枚举每个fruits中的元素，查找baskets中第一个大于等于fruits[i]且没被用过的篮子,如果直接从左往右暴力搜索，那总的时间复杂度将是O(n*m)，问题规模大一点将超时。对于枚举的fruits[i]，是否可以对baskets进行二分查找？若baskets是有序的，那当然可以，但现在它是无序的且不能对它排序。

线段树可以帮助对无序数组进行二分查找 ，用一个线段树维护baskets的区间最大值。

对于 x=fruits[i]，在线段树上二分查找第一个 ≥x 的数。

如果整个区间的最大值都小于 x，那么没有这样的数，直接返回 true，表示查找失败。
如果能递归到叶子，返回false，表示查找成功。
先递归左子树，如果左子树没找到，再递归右子树 (这样保证查找到的数在最左边)。
如果没有找到这样的数，把答案加一。

否则，把对应的位置改成 −1，然后向上更新修改，表示不能放水果。

代码

cpp 复制代码

class SegmentTree{
    vector<int>mx;
    void getmx(int f){
        mx[f]=max(mx[f<<1],mx[(f<<1)+1]);
    }
    void build(vector<int>&arr,int f,int l,int r){
        if(l==r){
            mx[f]=arr[l];
            return;
        }
        int m=(l+r)/2;
        build(arr,f<<1,l,m);
        build(arr,(f<<1)+1,m+1,r);
        getmx(f);    
    }
public:
    SegmentTree(vector<int>&arr){
        int n=arr.size();
        mx.resize(2<<bit_width((unsigned)(n-1)));
        build(arr,1,0,n-1);
    }
    bool findAndUpdate(int f,int l,int r,int x){
        if(mx[f]<x){
            return true;  //未找到，返回true
        }
        if(l==r){
            mx[f]=-1;  //找到具体元素，不能再用，标记为最小值-1
            return false;
        }
        int m=(l+r)/2;
        bool flat=findAndUpdate(f<<1,l,m,x);  //先找左子树
        if(flat){  //左子树找不到再找右子树
            flat=findAndUpdate((f<<1)+1,m+1,r,x);
        }
        getmx(f);  //向上更新区间最大值
        return flat;
    }
};
class Solution {
public:
    int numOfUnplacedFruits(vector<int>& fruits, vector<int>& baskets) {
        int n=baskets.size(),ans=0;
        SegmentTree tree(baskets);
        for(int i:fruits){
            if(tree.findAndUpdate(1,0,n-1,i)){
                ans++;  //为找到符合要求的篮子
            }
        }
        return ans;
        
    }
};