【数学基础（二）】向量、矩阵、行列式与线性变换

云茧2025-11-03 9:04

人工智能与世界模型# 系列文章目录

第一章 数学基础（一）导数、偏导数、方向导数与梯度

第二章 数学基础（二）向量、矩阵、行列式与线性变换

文章目录

  • [人工智能与世界模型# 系列文章目录](# 系列文章目录)
  • 前言
  • 一、向量
    • [1.1 什么是向量？](#1.1 什么是向量？)
    • [1.2 向量的核心运算](#1.2 向量的核心运算)
      • [1.2.1 基础运算](#1.2.1 基础运算)
      • [1.2.2 点积与叉积](#1.2.2 点积与叉积)
        • [点积（内积）： a ⋅ b = a 1 b 1 + a 2 b 2 + . . . + a n b n \mathbf{a}·\mathbf{b} = a_1b_1 + a_2b_2 + ... + a_nb_n a⋅b=a1b1+a2b2+...+anbn](#点积（内积）： a ⋅ b = a 1 b 1 + a 2 b 2 + . . . + a n b n \mathbf{a}·\mathbf{b} = a_1b_1 + a_2b_2 + ... + a_nb_n a⋅b=a1b1+a2b2+...+anbn)
        • [叉积（外积，仅三维向量）： a × b = [ a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ] \mathbf{a}×\mathbf{b} = [a_2b_3 - a_3b_2, a_3b_1 - a1b_3, a_1b_2 - a_2b_1] a×b=[a2b3−a3b2,a3b1−a1b3,a1b2−a2b1]](#叉积（外积，仅三维向量）： a × b = [ a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ] \mathbf{a}×\mathbf{b} = [a_2b_3 - a_3b_2, a_3b_1 - a1b_3, a_1b_2 - a_2b_1] a×b=[a2b3−a3b2,a3b1−a1b3,a1b2−a2b1])
    • [1.2 Numpy实现](#1.2 Numpy实现)
  • 二、矩阵
    • [2.1 什么是矩阵](#2.1 什么是矩阵)
    • [2.2 基础运算](#2.2 基础运算)
    • [2.3 特殊矩阵](#2.3 特殊矩阵)
    • [2.4 矩阵运算运用](#2.4 矩阵运算运用)
    • [2.5 Numpy实现矩阵运算](#2.5 Numpy实现矩阵运算)
  • 三、行列式
    • [3.1 什么是行列式](#3.1 什么是行列式)
    • [3.2 行列式的性质](#3.2 行列式的性质)
    • [3.3 行列式的计算方式](#3.3 行列式的计算方式)
    • [3.4 使用Numpy计算行列式](#3.4 使用Numpy计算行列式)
  • 四、线性变换
  • 五、知识点串联
    • [5.1 逻辑关系](#5.1 逻辑关系)
    • 注意点

前言

线性代数是 AI、计算机图形学、工程计算的核心数学基础，而向量、矩阵、行列式、线性变换贯穿其中。很多初学者会被抽象的符号和定理劝退，但其实它们的本质都能通过 "几何意义 + 实际应用" 理解。本文将从零基础出发，用通俗的语言拆解核心概念，搭配直观几何解释和可直接运行的 Numpy 代码，帮你真正吃透这些知识点，为后续学习 SVD、特征值分解、机器学习算法打下坚实基础。

  • 本系列默认读者有python基础

一、向量

1.1 什么是向量？

  • 代数定义：向量是有序的数字列表，比如二维向量 [x, y]、三维向量 [x, y, z]，n 维向量可表示为 v = [v₁, v₂, ..., vₙ]【行向量】或列向量【竖排形式】。
  • 几何意义：二维 / 三维向量是平面 / 空间中的 "箭头"------ 起点在原点，终点坐标对应向量的分量，核心属性是「方向」和「长度」（模）。

下图为[1,1]的向量：

  • 注意：向量没有 "位置"，只有方向和长度。比如 [1, 2] 和从点 (2,3) 指向 (3,5) 的向量是同一个向量（分量差相同）。

1.2 向量的核心运算

1.2.1 基础运算

运算 代数 几何意义
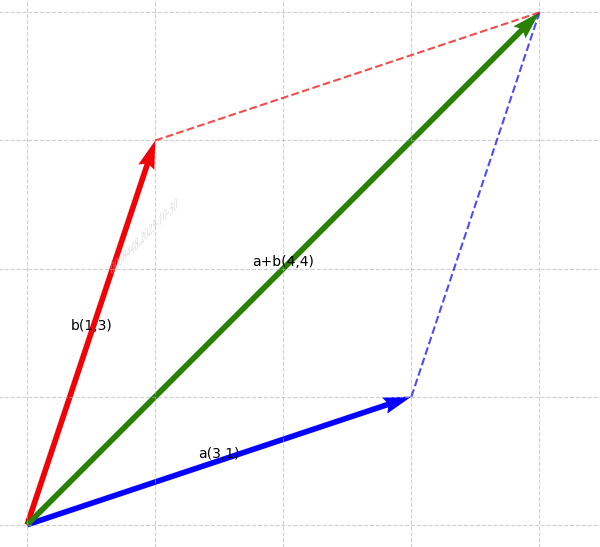
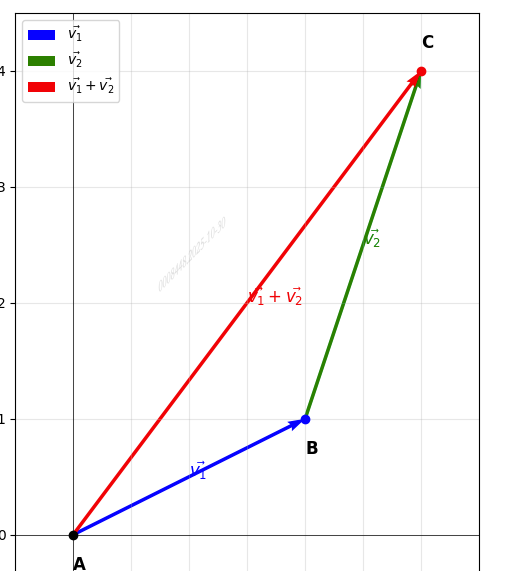
向量加法 a + b = [ a 1 + b 1 , a 2 + b 2 ] \mathbf{a} + \mathbf{b} = [a₁+b₁, a₂+b₂] a+b=[a1+b1,a2+b2] 平行四边形法则 / 三角形法则（首尾相接）
数乘 k ⋅ a = [ k ⋅ a 1 , k ⋅ a 2 ] （ k 为常数） k·\mathbf{a} = [k·a₁, k·a₂]（k 为常数） k⋅a=[k⋅a1,k⋅a2]（k为常数） 拉伸 / 压缩向量（k<0 时反向）
模(长度) ∣ ∣ a ∣ ∣ = ( a 1 2 + a 2 2 ) （ n 维同理求和开方） ||\mathbf{a}||=\sqrt {(a_1^2 + a_2^2)} （n 维同理求和开方） ∣∣a∣∣=(a12+a22) （n维同理求和开方） 箭头的长度
单位向量 a ^ = a ∣ ∣ a ∣ ∣ \hat{\mathbf{a}}=\frac{\mathbf{a}}{||\mathbf{a}||} a^=∣∣a∣∣a 保持方向，长度归一（用于表示方向）

平行四边形法则：

三角形法则：

1.2.2 点积与叉积

点积（内积）： a ⋅ b = a 1 b 1 + a 2 b 2 + . . . + a n b n \mathbf{a}·\mathbf{b} = a_1b_1 + a_2b_2 + ... + a_nb_n a⋅b=a1b1+a2b2+...+anbn

几何意义： a ⋅ b = ∣ ∣ a ∣ ∣ ⋅ ∣ ∣ b ∣ ∣ ⋅ c o s θ （ θ 是两向量夹角） \mathbf{a}·\mathbf{b} = ||\mathbf{a}||·||\mathbf{b}||·cos\theta（\theta是两向量夹角） a⋅b=∣∣a∣∣⋅∣∣b∣∣⋅cosθ（θ是两向量夹角），可用于：

  • 判断垂直: a ⋅ b = 0 \mathbf{a}·\mathbf{b} = 0 a⋅b=0时两向量垂直
  • 计算投影: 向量 a \mathbf{a} a在 b \mathbf{b} b方向的投影长度 = ( a ⋅ b ) ∣ ∣ b ∣ ∣ \frac{(\mathbf{a}·\mathbf{b})}{||\mathbf{b}||} ∣∣b∣∣(a⋅b)
  • 相似度: θ \theta θ越小或者点积越大，向量 a \mathbf{a} a和向量 b \mathbf{b} b的相似度越高
叉积（外积，仅三维向量）： a × b = [ a 2 b 3 − a 3 b 2 , a 3 b 1 − a 1 b 3 , a 1 b 2 − a 2 b 1 ] \mathbf{a}×\mathbf{b} = [a_2b_3 - a_3b_2, a_3b_1 - a1b_3, a_1b_2 - a_2b_1] a×b=[a2b3−a3b2,a3b1−a1b3,a1b2−a2b1]

几何意义：结果是垂直于 a \mathbf{a} a、 b \mathbf{b} b 所在平面的向量，模长 ∣ ∣ a × b ∣ ∣ = ∣ ∣ a ∣ ∣ ⋅ ∣ ∣ a ∣ ∣ ⋅ s i n θ ||\mathbf{a}×\mathbf{b}|| = ||\mathbf{a}||·||\mathbf{a}||·sin\theta ∣∣a×b∣∣=∣∣a∣∣⋅∣∣a∣∣⋅sinθ（等于以 a \mathbf{a} a、 b \mathbf{b} b 为邻边的平行四边形面积），可用于：

  • 判断平行： a × b = 0 \mathbf{a}×\mathbf{b} = 0 a×b=0时两向量平行
  • 确定法向量（图形学中经常用到）

1.2 Numpy实现

如果没有安装numpy，请先安装：

bash 复制代码 
pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple/

示例代码：

python 复制代码 
import numpy as np

# 1. 定义向量（行向量/列向量）
row_vec = np.array([1, 2, 3])  # 行向量
col_vec = np.array([[1], [2], [3]])  # 列向量（二维数组表示）

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 2. 基本运算
vec_add = a + b  # 向量加法：[5 7 9]
a_scalar = 2 * a  # 数乘：[2 4 6]
a_norm = np.linalg.norm(a)  # 模长：√(1+4+9)=√14≈3.7417
a_unit_vec = a / a_norm  # 单位向量

# 3. 点积与叉积
dot_product = np.dot(a, b)  # 点积：1*4 + 2*5 +3*6=32
cross_product = np.cross(a, b)  # 叉积：[2*6-3*5, 3*4-1*6, 1*5-2*4] = [-3,6,-3]

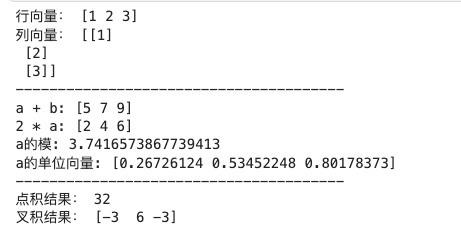
print("行向量：", row_vec)
print("列向量：", col_vec)
print("---------------------------------------")
print("a + b:", vec_add)
print("2 * a:", a_scalar)
print("a的模:", a_norm)
print("a的单位向量:", a_unit_vec)
print("---------------------------------------")
print("点积结果：", dot_product)
print("叉积结果：", cross_product)

运行结果：

二、矩阵

2.1 什么是矩阵

  • 定义：矩阵是 m 行 n 列的数字矩形阵列，记为 A ∈ R ( m × n ) \mathbf{A} \in R^{(m×n)} A∈R(m×n)（m 行 n 列，元素为实数），比如：
    A = [ 1 2 3 4 5 6 7 8 9 ] \mathbf{A} = \begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9 \end{bmatrix} A= 147258369
  • 代数意义：从代数角度看，矩阵乘以向量的结果，是矩阵的列向量以向量的分量为权重的线性组合。设矩阵 A 的列向量为 a₁, a₂, ..., aₙ，向量 x = [x₁, x₂, ..., xₙ]ᵀ，那么：A * x = x₁a₁ + x₂a₂ + ... + xₙ*aₙ
  • 几何意义：矩阵是「线性变换的载体」------ 用矩阵乘以向量，本质是对向量进行 "旋转、缩放、剪切" 等变换（后续线性变换章节详细讲）
  • 核心用途：表示线性方程组、存储数据（如一张图片可视为像素值矩阵）、描述变换规则。

2.2 基础运算

运算 规则说明 注意事项
矩阵加法 同形状矩阵（m×n）对应元素相加 不同形状无法相加
数乘 常数 k 乘矩阵所有元素 不改变矩阵形状
矩阵乘法 若 A 是 m×p 矩阵，B 是 p×n 矩阵，则 AB 是 m×n 矩阵；AB [i][j] = A 第 i 行・B 第 j 列（点积） 不满足交换律（AB≠BA），满足结合律
转置 行变列、列变行，记为 A T ; ( A B ) T = B T A T ) \mathbf{A}^T; (\mathbf{AB})^T = B^TA^T) AT;(AB)T=BTAT) 对称矩阵满足 A T = A \mathbf{A}^T = \mathbf{A} AT=A
逆矩阵 若存在 A − 1 \mathbf{A}^{-1} A−1，使得 A A − 1 = A − 1 A = I \mathbf{A}\mathbf{A}^{-1} = \mathbf{A}^{-1}\mathbf{A} = I AA−1=A−1A=I（单位矩阵），则 A \mathbf{A} A 可逆 仅方阵（m=n）可能可逆；行列式≠0 是可逆的充要条件

2.3 特殊矩阵

  • 单位矩阵 I I I：对角线元素为 1，其余为 0，比如 2×2 单位矩阵 [[1,0],[0,1]]；作用：乘以任何矩阵 / 向量不变（类似数字 1）。
  • 零矩阵 O O O：所有元素为 0，作用：类似数字 0， A + O = A A+O=A A+O=A。
  • 对称矩阵： A T = A A^T = A AT=A（对角线对称），比如 [[1,2],[2,3]]，常见于协方差矩阵。
  • 正交矩阵： A T = A − 1 A^T = A^{-1} AT=A−1（转置等于逆），作用：对向量旋转 / 反射变换，不改变向量长度（图形学常用）。

本文由于篇幅问题仅作引出，后续用到之前会单独开一篇帖子讲解，所有大家现在先不用钻对称矩阵和正交矩阵为什么这样的牛角尖。先有一个整体概念即可。

2.4 矩阵运算运用

需求：你有现在手里有64个股票的数据，分别为每只股票的收盘价( x 1 x_1 x1)、成交量( x 2 x_2 x2)、涨跌幅( x 3 x_3 x3)及市盈率( x 4 x_4 x4)，假设现在你手里面有一个非常nice的函数可以非常准确的预测明天的开盘价，公式如下：

明天开盘价 = H ( x 1 , x 2 , x 3 , x 4 ) = 0.95 x 1 + 0.0001 x 2 − 1.1 x 3 + 0.9 x 4 明天开盘价 = H(x_1,x_2,x_3,x_4) = 0.95x_1 + 0.0001x2 - 1.1x_3 + 0.9x_4 明天开盘价=H(x1,x2,x3,x4)=0.95x1+0.0001x2−1.1x3+0.9x4(本公式纯属胡扯，教学使用)

计算出64个股票的明天开盘价

  • 传统方式：写一个循环遍历每个股票过一遍函数

  • 矩阵方式：

    将股票数据存储为一个（64, 4）的矩阵 X X X，每一行存储一个股票的数据，声明一个[[0.95], [0.00001], [-1.1], [0.9]]的列向量（4, 1） W W W

    这时通过一次矩阵 X X X乘上向量 W W W的方式，一次性将64个预测值计算了出来

    明天开盘价 = X ⋅ W X·W X⋅W

    结果为(64, 1)的列向量，其中每一行的那个值就是每只股票计算出来的预测值

2.5 Numpy实现矩阵运算

代码示例：

python 复制代码 
import numpy as np

# 1. 定义矩阵
A = np.array([[1, 2], [3, 4]])  # 2×2矩阵
B = np.array([[5, 6], [7, 8]])  # 2×2矩阵
v = np.array([1, 0])  # 向量

# 2. 基础运算
mat_add = A + B  # 矩阵加法：[[6,8],[10,12]]
mat_scalar = 2 * A  # 数乘：[[2,4],[6,8]]
mat_mul = np.dot(A, B)  # 矩阵乘法：[[1*5+2*7, 1*6+2*8], [3*5+4*7, 3*6+4*8]] = [[19,22],[43,50]]
mat_transpose = A.T  # 转置：[[1,3],[2,4]]

print("A + B:\n", mat_add, '\n')
print("2 * A:\n", mat_add, '\n')
print("A · B:\n", mat_mul, '\n')
print("A^T:\n ", mat_transpose, '\n')

print("----------------------------------------------------")

# 3. 逆矩阵（仅方阵）
if np.linalg.det(A) != 0:  # 判断行列式≠0（可逆）
    A_inv = np.linalg.inv(A)  # 逆矩阵：[[-2,1],[1.5,-0.5]]
    print("A的逆矩阵：\n", A_inv, '\n')
    print("A·A⁻¹ = \n", np.dot(A, A_inv), '\n')  # 结果接近单位矩阵（浮点误差）

# 4. 矩阵乘向量（向量变换）
v_transformed = np.dot(A, v)  # 变换后的向量：[1*1+2*0, 3*1+4*0] = [1,3]
print("向量v经矩阵A变换后：", v_transformed)

运行结果：

三、行列式

3.1 什么是行列式

行列式是一个与方阵关联的标量值。可以看作是一种对方阵进行数值化描述的方法，通过它可以获取到矩阵的一些重要信息。仅方阵有行列式（记为 det (A) 或 |A|）

  • 几何意义：行列式的绝对值是「矩阵对应的线性变换对空间的缩放比例」：
    2×2 矩阵：|det (A)| 是变换后单位正方形的面积；
    3×3 矩阵：|det (A)| 是变换后单位立方体的体积；
    若 det (A)=0：变换后空间被 "压缩" 到更低维度（比如平面压成直线），信息有所缺失，所以矩阵不可逆；
    若 det (A)<0：变换包含 "镜像翻转"（改变空间定向）。

3.2 行列式的性质

  1. 行 / 列互换，行列式值不变；
  2. 某行 / 列乘以常数 k，行列式变为 k・det (A)；
  3. 两行 / 列交换，行列式变号；
  4. 若两行 / 列成比例，det (A)=0（矩阵不可逆）；
  5. det (AB) = det (A)・det (B)（乘积的行列式 = 行列式的乘积）；
  6. d e t ( A − 1 ) = 1 / d e t ( A ) det (A^{-1}) = 1/det (A) det(A−1)=1/det(A)（逆矩阵的行列式 = 原行列式的倒数）。

3.3 行列式的计算方式

不做重点，感兴趣的可以看看下面这个帖子
行列式的计算方式

3.4 使用Numpy计算行列式

示例代码：

python 复制代码 
import numpy as np

# 1. 计算行列式
A = np.array([[1, 2], [3, 4]])
det_A = np.linalg.det(A)  # 2×2行列式：1*4 - 2*3 = -2
print("det(A) =", det_A)

B = np.array([[1, 0, 0], [0, 2, 0], [0, 0, 3]])  # 对角矩阵
det_B = np.linalg.det(B)  # 对角矩阵行列式=对角线元素乘积：1*2*3=6
print("det(B) =", det_B)

# 2. 验证性质：det(AB) = det(A)·det(B)
AB = np.dot(A, np.array([[2,0],[0,1]]))  # A乘以对角矩阵
det_AB = np.linalg.det(AB)
det_A_det_B = det_A * np.linalg.det(np.array([[2,0],[0,1]]))
print("det(AB) =", det_AB)
print("det(A)·det(B) =", det_A_det_B)  # 结果相等（-4 = -2*2）

# 3. 行列式=0的矩阵（不可逆）
C = np.array([[1, 2], [2, 4]])  # 第二行是第一行的2倍
det_C = np.linalg.det(C)  # 1*4 - 2*2 = 0
print("det(C) =", det_C)
# np.linalg.inv(C)  # 报错：LinAlgError（奇异矩阵，不可逆）

运行结果：

四、线性变换

  • 定义 ：满足两个条件的变换 T（输入向量→输出向量）：
    可加性：T (u + v) = T (u) + T (v)
    齐次性：T (k・v) = k・T (v)（k 为常数）
  • 通俗理解：变换后「直线仍为直线，原点保持不变」，没有 "弯曲" 或 "平移"（平移是非线性变换）。
  • 核心结论 ：所有线性变换都可以用矩阵表示------ 若 T 是 Rⁿ→Rᵐ的线性变换，则存在 m×n 矩阵 A，使得 T (v) = A・v（矩阵乘向量）。

五、知识点串联

5.1 逻辑关系

向量 → 矩阵（向量的变换规则）→ 行列式（矩阵变换的缩放比例）→ 线性变换（矩阵的本质）

  • 向量是变换的 "对象"；
  • 矩阵是变换的 "规则"；
  • 行列式是变换的 "副作用"（缩放 / 降维）；
  • 线性变换是矩阵的 "数学本质"（所有矩阵都对应唯一线性变换，反之亦然）。

注意点

  1. 矩阵乘法不满足交换律：AB≠BA（变换顺序影响结果，比如先旋转后缩放≠先缩放后旋转）；
  2. 只有方阵有行列式和逆矩阵：非方阵（如 2×3 矩阵）无法计算行列式，也不可逆；
  3. 行列式 = 0 → 矩阵不可逆 → 线性变换降维（空间被压缩）；
  4. 向量的点积是标量，叉积是向量（仅三维）。

本文为个人见解，如有错误，评论区指出

相关推荐
无风听海8 小时前
神经网络之PPMI矩阵
人工智能·神经网络·矩阵
短视频矩阵源码定制17 小时前
矩阵系统源码推荐：技术架构与功能完备性深度解析
java·人工智能·矩阵·架构
AI Chen19 小时前
【矩阵分析与应用】【第5章 梯度分析与最优化】【5.2.2 矩阵迹的微分计算示例d(tr(U))=tr(dU)证明】
矩阵·迹
短视频矩阵源码定制19 小时前
矩阵系统全面解析：构建智能营销体系的核心引擎
java·人工智能·矩阵·aigc·视频
知识搬运工人2 天前
传统卷积神经网络中的核心运算是卷积或者矩阵乘，请问transformer模型架构主要的计算
矩阵·cnn·transformer
前端炒粉3 天前
18.矩阵置零（原地算法）
javascript·线性代数·算法·矩阵
AI Chen3 天前
【矩阵分析与应用】【第1章 矩阵与线性方程组】【1.6.2.2 迹的循环置换性质】
矩阵·迹
大千AI助手3 天前
HOSVD（高阶奇异值分解）：高维数据的“解剖术”
人工智能·线性代数·矩阵·张量·svd·hosvd·高阶奇异值分解
marsggbo3 天前
尝试从源头理解 SVD 原理和计算
线性代数·奇异值分解·svd
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04《大数据技术原理与应用》实验报告三 熟悉HBase常用操作05Linux下V2Ray安装配置指南06GitLab 零基础入门指南：从安装到项目管理全流程07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09jdk21下载、安装（Windows、Linux、macOS）10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）