极限挑战之一命速通哈夫曼树

在我上一篇关于并查集的博客中，我们探讨了如何高效处理不相交集合的合并与查询问题。今天，我们将继续探索树结构的另一个精彩应用------哈夫曼树与编码。如果说并查集解决了数据的连通性问题，那么哈夫曼树则专注于数据的压缩问题， 它们都是树这种数据结构在不同领域的绝妙展现

1. 初识哈夫曼树

1.1 哈夫曼树的基本概念

哈夫曼树（Huffman Tree），又称最优二叉树，是一种带权路径长度最短的二叉树。它由大卫·哈夫曼于1952年提出，但这个算法至今仍是数据压缩领域的基石之一

1.2 带权路径长度

要明白哈夫曼树为什么是最优的二叉树，我们首先要了解带权路径长度这个概念

带权路径长度： 任意二叉树中其所有叶子节点的权值（可理解为出现频率、重要程度等） 乘以其到根节点的路径长度（可理解为编码长度） 之和，用数学公式可表示为：*WPL = ∑(权值 × 路径长度)

哈夫曼树之所以"最优"，就是因为它能构造出WPL最小的二叉树结构

1.3 哈夫曼编码

哈夫曼编码 是一种变长前缀编码，基于哈夫曼树（最优二叉树）实现，核心原理是让出现频率高的字符获得短编码，频率低的字符获得长编码， 从而最小化整体编码长度（即带权路径长度 WPL），实现高效的数据压缩~

想象一下，我们要传递一串字符信息，如果每个字符都用相同长度的二进制码表示，固然简单，但却不是最高效的方式。哈夫曼编码的核心思想是：​根据字符出现的频率，为高频字符分配短编码，低频字符分配长编码，从而减少整体编码长度

举个例子吧，这就像现实生活中我们常用"OK"、"嗨"等简短表达来表示高频交流，而用较长的词汇表达复杂概念。哈夫曼树正是将这种智慧应用到了数据编码中

1.4 哈夫曼编码核心原理步骤

1.4.1 统计字符频率（权值）

首先对需要编码的字符集合，统计每个字符的出现频率，将其作为哈夫曼树中叶子节点的权值

1.4.2 构建哈夫曼树

按照 "反复合并权值最小的两个节点" 的规则构建哈夫曼树：

• 初始时，每个字符对应一个权值为其频率的叶子节点
• 每次选择权值最小的两个节点，合并为一个新的内部节点（权值为两子节点权值之和）（选过的节点不能再选噢）
• 重复此过程，直到所有节点合并为一棵二叉树（根节点权值为所有字符频率之和）

1.4.3 生成哈夫曼编码

从哈夫曼树的根节点到叶子节点，规定：

• 在哈夫曼编码中，根节点没有编码
• 左分支标记为0，右分支标记为1
• 每个叶子节点对应的路径上的 0/1 序列，即为该字符的哈夫曼编码

1.4.4 前缀编码特性（无歧义解码）

通过哈夫曼编码的核心原理步骤我们不难发现，它不像二进制编码那样会有歧义的出现，这是因为哈夫曼编码是前缀编码：即任何一个字符的编码都不是另一个字符编码的 "前缀"。 例如，若字符A的编码是01，则其他字符的编码绝不会以01开头。这一特性保证了解码时能唯一、无歧义地分割编码序列~

1.5 哈夫曼树核心目标：最小化编码 / 存储的总代价

哈夫曼树主要用于数据压缩（如哈夫曼编码）和最优决策（如判定树）等场景。在这些场景中，我们希望对出现频率不同的元素进行编码或处理时，整体代价最小~

这里的"整体代价最小"，核心就是指带权路径长度（WPL）最小， 我们不妨结合下具体应用场景进行理解：

• 在哈夫曼编码（数据压缩）中：权值是字符的出现频率，路径长度是字符的编码位数。 "整体代价最小" 即 "所有字符的（出现频率 × 编码位数）之和最小"。比如高频字符用短编码、低频字符用长编码，最终整个文本的编码总长度（存储/传输代价）最优
• 在最优判定树中：权值是事件的发生概率，路径长度是判定的步骤数。 "整体代价最小" 即 "所有事件的（发生概率 × 判定步骤数）之和最小"，从而让整个判定过程的平均耗时/成本最优

简言之，它是通过让权重大（高频/高概率）的元素路径更短，实现整体资源（存储、时间、成本等）的最优利用

归根结底还是数据结构在不同应用场景下对时空复杂度的极致追求罢了

2. 构建哈夫曼树

2.1 哈夫曼树存储方式选择

在理解哈夫曼编码原理后，就要用代码来实现它了。这时问题来了：我们该如何在内存中表示这棵树？

先回忆一下，在我们目前所学习过的那么多种数据结构中，无非就是使用链式存储或顺序存储，所以我们就是在此之间进行二选一罢了

那该选什么呢？我们不妨根据哈夫曼编码的性质对两种不同的存储方式进行对比

• 链式存储（直观但复杂）​​：

  我们可以像之前设计树结构一样，为每个节点设计一个结构体，包含权重、指向左孩子和右孩子的指针等。这种方法虽然直观反映了树的形状，但在构建过程中，需要频繁地创建新节点、链接指针，管理起来相对复杂

• 顺序存储（表格法，高效且巧妙）​​：

  • 内存紧凑： 哈夫曼树是严格二叉树（所有节点都有0或2个孩子），如果有 n=8个叶子节点，就必然有 n-1=7个分支节点，总节点数 m = 2n-1 = 15是确定的。我们可以一次性分配一个大小为15的数组，没有内存碎片
  • 操作高效​： 同时构建过程的核心是"寻找权重最小的两个节点"。在数组中通过下标遍历和比较，速度非常快
  • 过程清晰​： 且整个构建过程就像填表一样，每一步都记录在案，最终表格本身就是一棵完整的树，简直不要太完美

2.2 哈夫曼树表格构建法

哈夫曼树的表格通常成下列形态，现在我来对此进行详细讲解

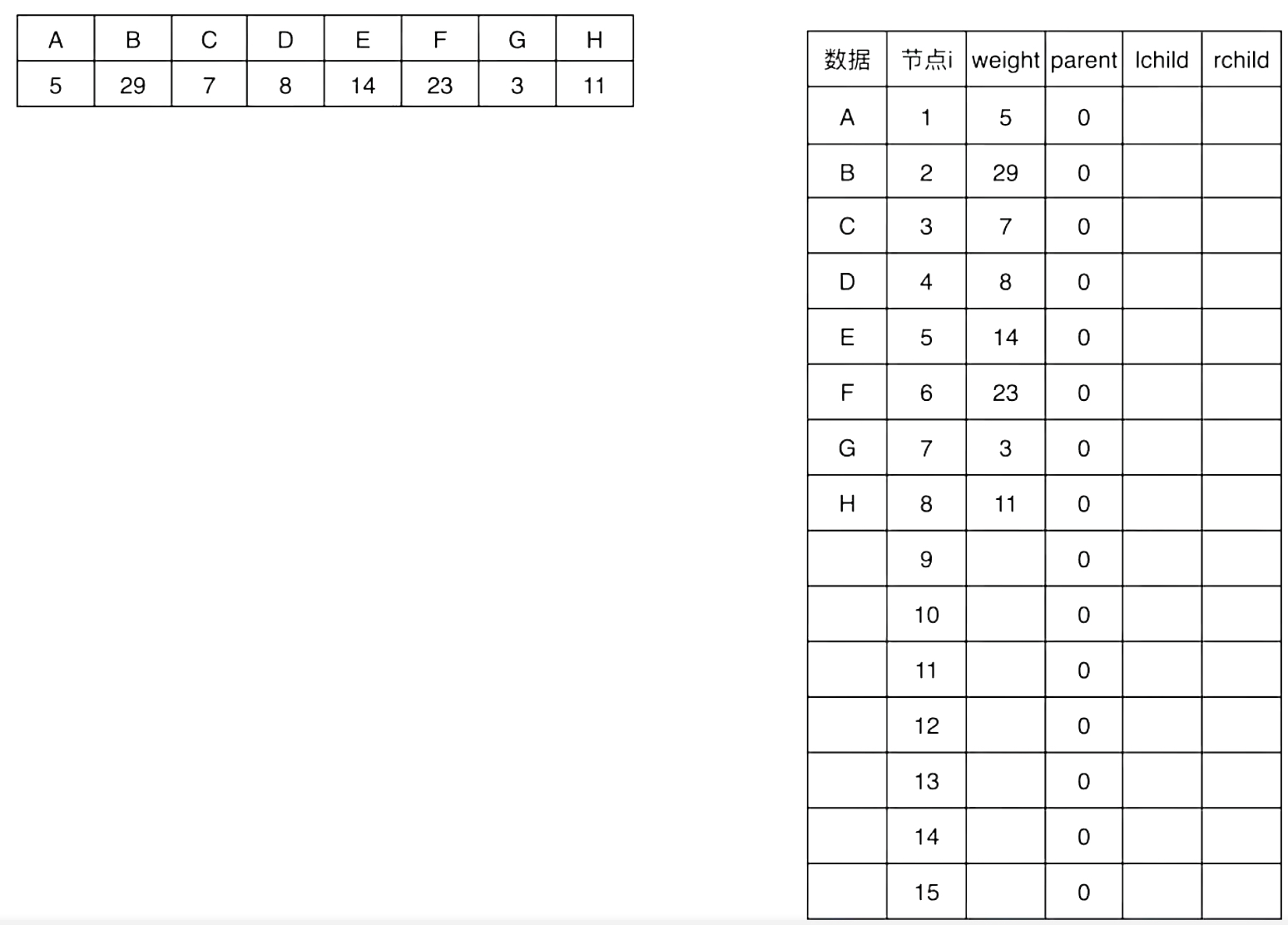
• 节点i （数组下标）​​： 每个节点的唯一ID，可以看作是它在数组中的"房间号"。1-8号房间住的是初始的叶子节点（A-H），9-15号房间是为构建过程中新产生的分支节点预留的
• weight（权重）： 该节点所代表的权重值。对于叶子节点，就是字符的出现频率；对于分支节点，则是其左右孩子权重之和
• ​parent（父节点）​​： 该节点的父亲住在哪个"房间号"（即数组下标）。这是实现逆向生成编码的关键。根节点的父节点为0，表示它没有父亲
• ​lchild（左孩子）： 该节点的左孩子住在哪个"房间号"。叶子节点没有孩子，故此列为空
• rchild（右孩子）​​： 该节点的右孩子住在哪个"房间号"。叶子节点没有孩子，故此列为空

现在让我们亲手把这张空表填满，同时别忘了其​核心步骤永远是：在所有 parent为0的节点中，找出两个权重最小的，合并它们

2.2.1 第1次合并：找当前最小的两个节点​

• 最小：​​ G(节点7, weight=3)
• 次小：​​ A(节点1, weight=5)
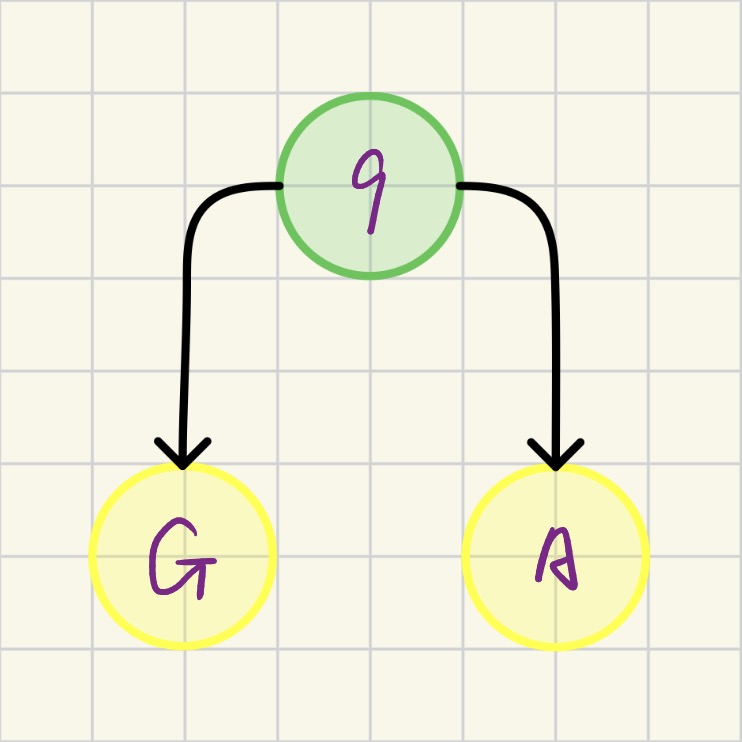
• 操作：创建一个新父亲节点，放在下一个空闲位置，即节点9，并设置节点9的weight = 3 + 5 = 8，lchild = 7(指向G)、rchild = 1(指向A)，同时更新孩子节点的父节点，将G(7)和A(1)的parent都设为9。此时，节点9的parent仍为0，参与后续合并

操作后如图所示：

下列图示中黄色节点为表格中已有的节点，绿色节点为合并后新创建的节点

2.2.2 第2次合并​

当前parent=0的节点有：​​B(29), C(7), D(8), E(14), F(23), H(11), 以及新成员9(8)​

• 最小：​​ C(节点3, weight=7)
• 次小： D(节点4, weight=8)（注意，节点9的权重也是8，但通常先取原节点或按下标顺序，算法结果可能不同，但WPL相同）
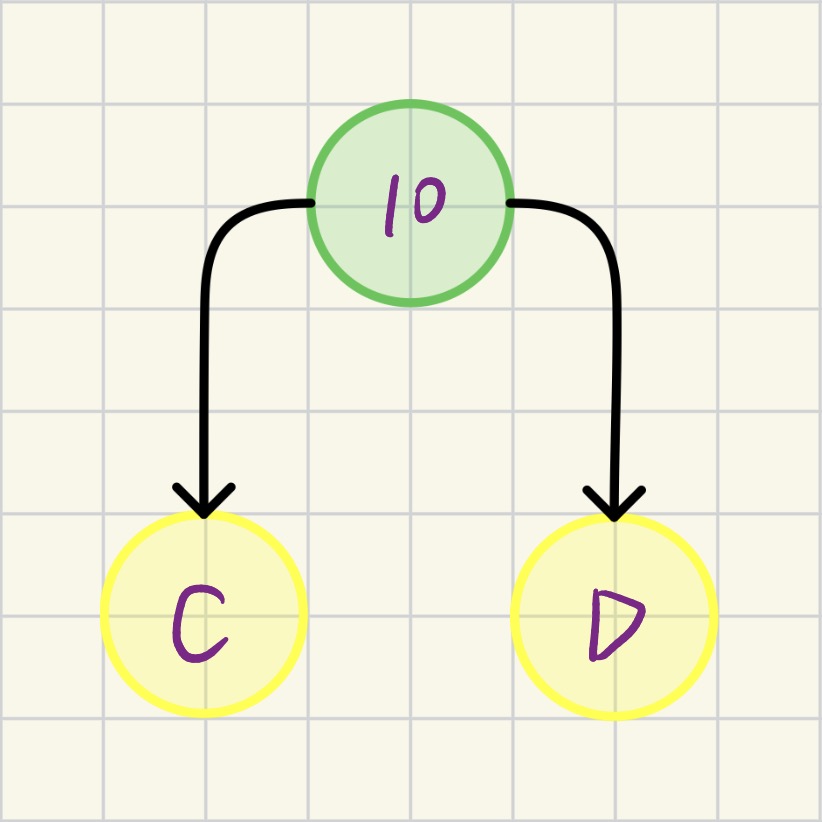
• 操作： 合并C和D，产生节点10(weight=15)，并更新节点C、D的parent为10及节点10的左右孩子分别为节点C、D

操作后如图所示：

2.2.3 第3次合并​

当前 parent=0的节点：​​ B(29), E(14), F(23), H(11), 9(8), 10(15)

• 最小： 节点9 (weight=8)
• 次小： H (节点8, weight=11)
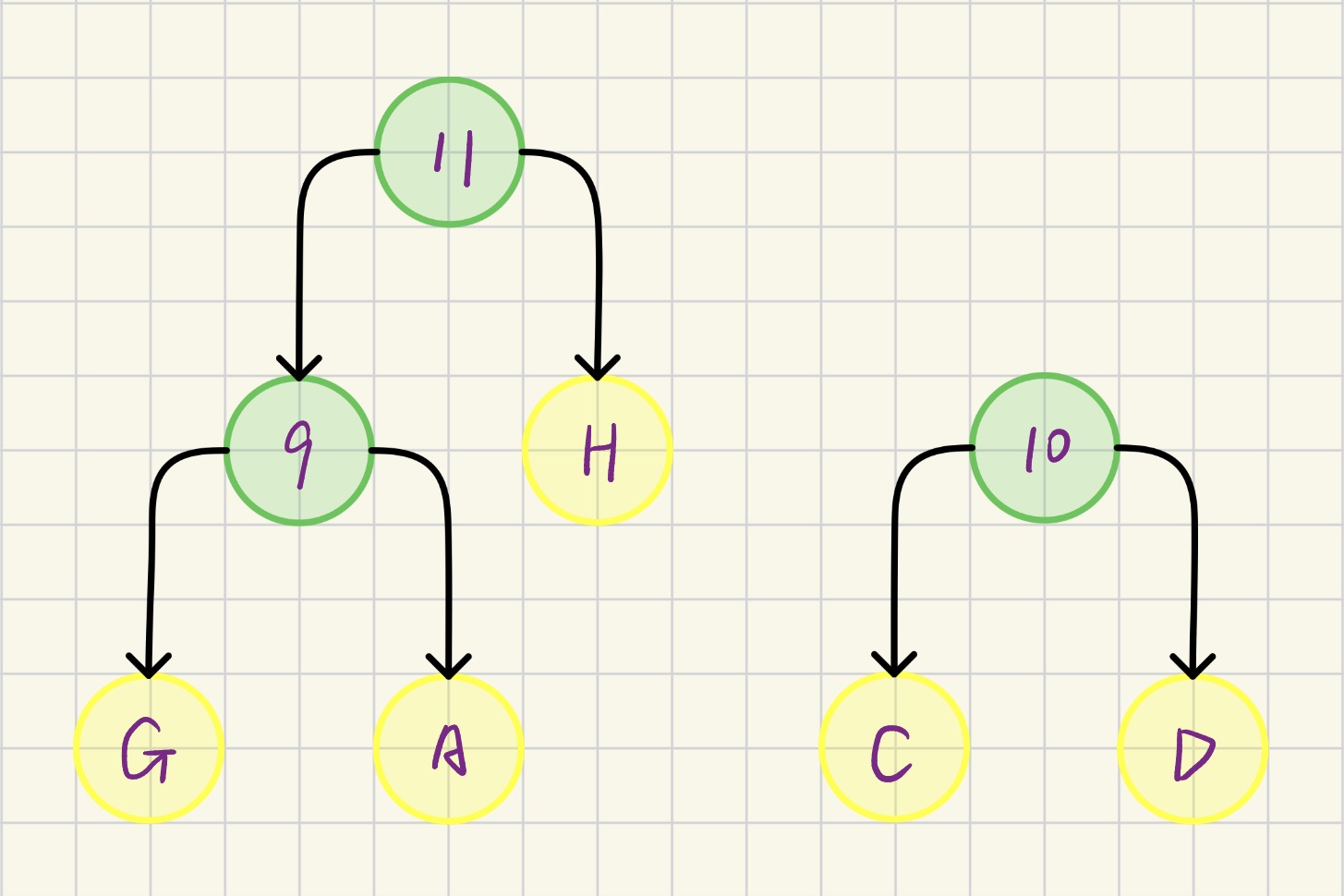
• ​操作：​​ 合并节点9和H，产生节点11(weight=19)，并更新节点9、H的parent为11及节点11的左右孩子分别为节点9、H

操作后如图所示：

...... 依此类推 ......

2.2.7 第7次合并（最后一次）​​

此时，经过前6次合并，生成了节点9到节点14。现在只剩下两个 parent=0的节点

最小： 节点13(weight=42, 它是之前一系列合并的最终产物)
次小： 节点14(weight=58, 它是B和节点12的父节点)

​操作：​​ 合并节点13和节点14，产生根节点15(weight=42+58=100)，并

设置节点15的lchild = 13、rchild = 14，同时更新节点13、14的parent为15。此时根节点15的parent设置为0

操作后如图所示：

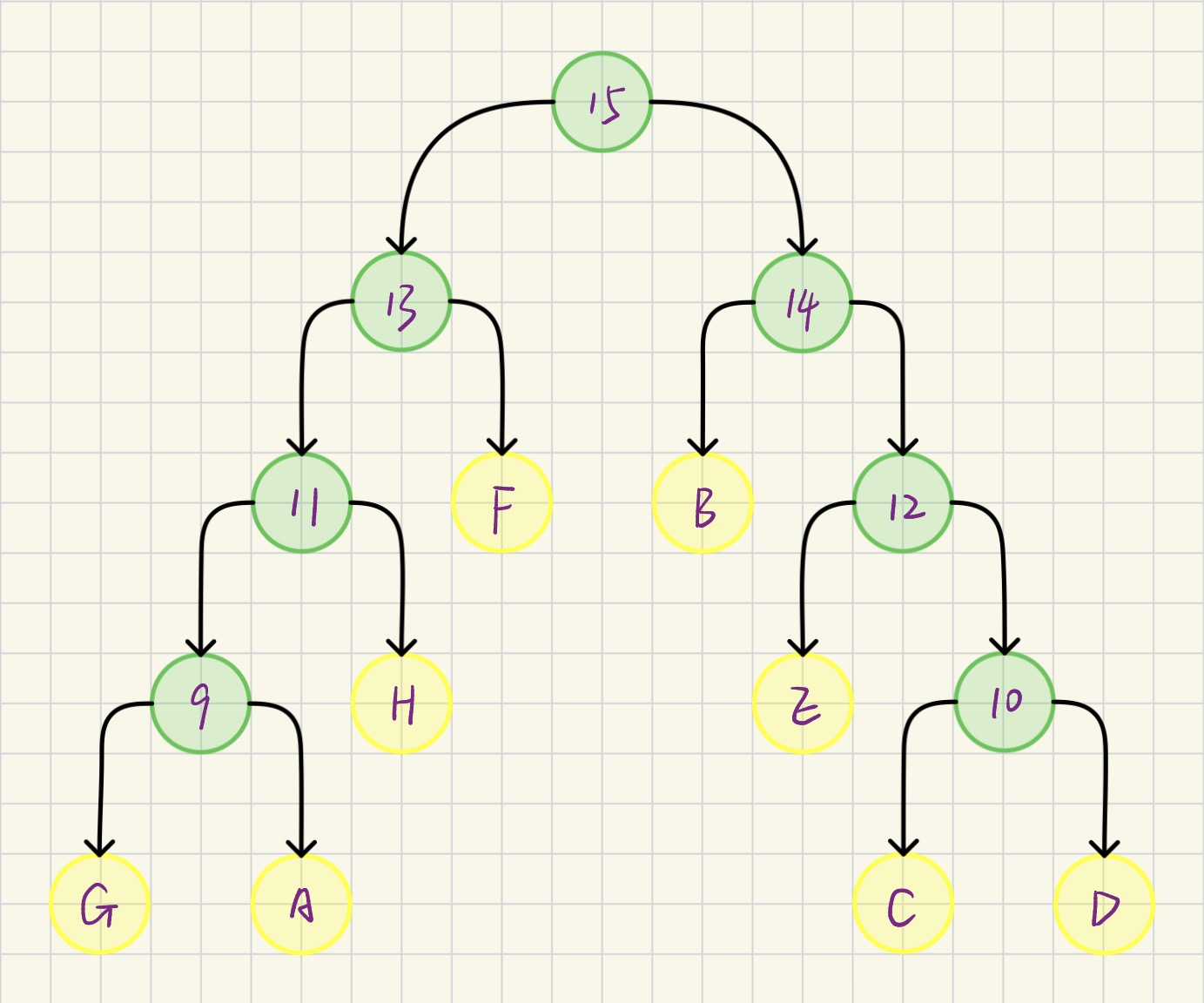
最后的表格填写结果如下：

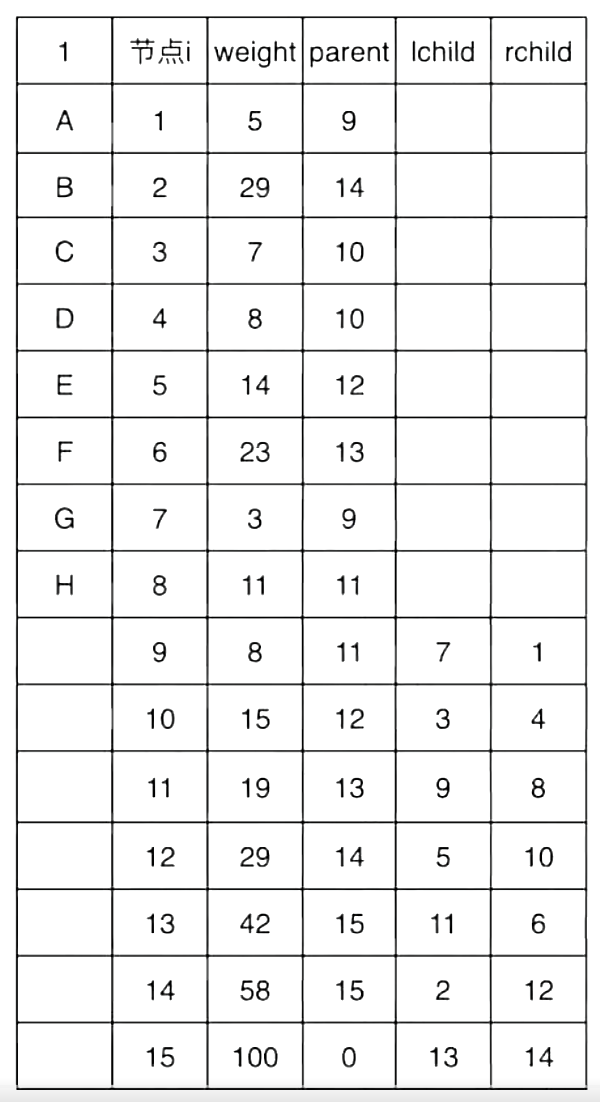
2.3 哈夫曼树节点数据结构定义

由上述图示和哈夫曼树采用顺序存储的方式不难得出，其基本数据结构定义如下：

// 定义Huffman树的节点结构，采用顺序存储方式，下标索引来标识不同的节点
typedef struct {
	// 节点权值（字符出现频率）
	int weight;
	int parent;
	int lChild;
	int rChild;
} HuffmanNode, * HuffmanTree;

2.4 哈夫曼树选择最小权值节点

这是构建哈夫曼树的关键步骤

static void selectNode(HuffmanTree tree, int n, int* s1, int* s2) {
	// 临时变量，用于记录当前最小权值节点的下标
	int mini = 0;
	
	// 找到第一个父节点为0的编号
	for (int i = 1; i <= n; ++i) {
		// 只考虑尚未被合并的节点
		if (tree[i].parent == 0) {
			// 记录第一个可用节点的下标
			mini = i;
			break;
		}
	}

	// 遍历所有节点，找到权值最小的节点
	for (int i = 1; i <= n; ++i) {
		// 确保节点未被处理
		if (tree[i].parent == 0) {
			if (tree[i].weight < tree[mini].weight) {
				mini = i;
			}
		}
	}
	// 将第一个最小权值节点下标保存到s1
	*s1 = mini;

	// 第二轮查找：找到第二个最小权值节点
  // 重新初始化mini，寻找第一个不等于s1且未被处理的节点
	for (int i = 1; i <= n; ++i) {
		// 排除已找到的第一个最小节点
		if (tree[i].parent == 0 && i != *s1) {
			// 更新最小权值节点下标
			mini = i;
			break;
		}
	}

	// 遍历找到第二个最小权值节点
	for (int i = 1; i <= n; ++i) {
		// 确保不是s1且未被处理
		if (tree[i].parent == 0 && i != *s1) {
			if (tree[i].weight < tree[mini].weight) {
				// 更新第二个最小权值节点
				mini = i;
			}
		}
	}
	// 将第二个最小权值节点下标保存到s2
	*s2 = mini;
}

这个函数实现了贪心算法的核心思想，即每次选择局部最优解。通过两次独立的查找过程，确保找到真正最小的两个节点

2.5 初始化哈夫曼树

这是整个算法的核心函数，实现了哈夫曼树的构建逻辑

HuffmanTree createHuffmanTree(const int* w, int n) {
	HuffmanTree tree;
	// 计算哈夫曼树的总节点数（n个叶子节点产生n-1个内部节点）
	// 总结点数为2n - 1
	int m = 2 * n - 1;
	
	// 1.1 申请m+1个节点的内存空间（从下标1开始使用，0号位置空闲）
	tree = malloc(sizeof(HuffmanNode) * (m + 1));
	if (tree == NULL) {
		return NULL;
	}
	
	// 1.2 初始化1 ~ m个节点的属性
	for (int i = 1; i <= m; ++i) {
		tree[i].parent = tree[i].lChild = tree[i].rChild = 0;
		tree[i].weight = 0;
	}
	
	// 1.3 设置前n个叶子节点的初始权值（从参数w中读取）
	for (int i = 1; i <= n; ++i) {
		// w[0]对应tree[1]，以此类推
		tree[i].weight = w[i - 1];
	}
	
	// 1.4 填充n+1下标到m下标的空间
	int s1, s2;

	// 1.5 构建哈夫曼树：填充n+1到m的内部节点
	for (int i = n + 1; i <= m; ++i) {
		// 在当前已有节点中（1到i-1）选择两个权值最小且未被合并的节点
		selectNode(tree, i - 1, &s1, &s2);
		// 将选出的两个最小节点合并到第i个位置（新创建的内部节点）
		tree[s1].parent = tree[s2].parent = i;
		tree[i].lChild = s1;
		tree[i].rChild = s2;
		tree[i].weight = tree[s1].weight + tree[s2].weight;
	}
	return tree;
} 

根据图示并结合这段函数我们不难发现，这个函数充分体现了哈夫曼算法的精髓，即自底向上的合并策略。整个过程可以理解为先准备n个孤立的叶子节点，再重复n-1次合并操作，每次选择两个最小节点合并，最后当只剩下一个节点时（根节点），则说明构建完成。 这种设计保证了最终得到的哈夫曼树是带权路径长度最短的二叉树~

3. 生成哈夫曼编码：从树结构到二进制编码

构建好哈夫曼树后，我们需要为每个字符生成对应的变长编码

HuffmanCode* createHuffmanCode(HuffmanTree tree, int n) {
	// 生成n个字符的编码表，每个表项保存对应字符编码的空间首地址
	HuffmanCode* codes = malloc(sizeof(HuffmanCode) * n);
	if (codes == NULL) {
		return NULL;
	}
	// 初始化编码表为NULL
	memset(codes, 0, sizeof(HuffmanCode) * n);
	
	// 每求一个字符时，倒序构建，n个节点，树的高度最高是n，编码个数最多为n
	char* temp = malloc(sizeof(char) * n);
	// temp空间的起始位置指针
	int start;
	// 存放当前节点的父节点信息
	int p;
	// 当前处理的节点位置
	int pos;
	
	// 逐个字符求Huffman编码
	for (int i = 1; i <= n; ++i) {
		// 从临时数组末尾开始填充（倒序构建）
		start = n - 1;
		// 字符串结束标志
		temp[start] = '\0';
		// 从当前叶子节点开始
		pos = i;
		// 获取当前节点的父节点
		p = tree[i].parent;

		// 从叶子节点向上遍历到根节点
		while (p) {
			// 向前移动存储位置
			--start;
			// 判断当前节点是父节点的左孩子还是右孩子
			// 左孩子编码为'0'，右孩子编码为'1'
			temp[start] = (tree[p].lChild == pos) ? '0' : '1';
			// 移动到父节点
			pos = p;
			// 继续向上遍历
			p = tree[p].parent;
		}
		

		// 为第i个字符编码分配确切大小的空间
		codes[i - 1] = malloc(sizeof(HuffmanCode) * (n - start));
		// 复制编码到最终存储位置
		strcpy(codes[i - 1], &temp[start]);
	}
	// 释放临时空间
	free(temp);
	// 返回生成的编码表
	return codes;
}

在这里，编码生成的关键有：

• 倒序构建策略​： 由于从叶子到根的路径是逆向的，故我们采用从后向前填充的方式
• 动态内存分配​： 根据每个编码的实际长度分配合适的内存空间，避免浪费
• 路径记录​： 通过判断当前节点是左孩子还是右孩子来确定编码位（0或1）

4. 哈夫曼编码测试

写一个小小的测试案例看一下能否正确生成哈夫曼编码吧~

int main() {
	int w[] = { 5, 29, 7, 8, 14, 23, 3, 11 };
	char show[] = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H' };
	int n = sizeof(w) / sizeof(w[0]);
	HuffmanTree tree = createHuffmanTree(w, sizeof(w) / sizeof(w[0]));
	HuffmanCode* codes = createHuffmanCode(tree, n);
	for (int i = 0; i < n; i++) {
		printf("%c: %s\n", show[i], codes[i]);
	}
	// releaseHuffmanCode(codes, n);
}

结合测试结果及图示对比看一下~

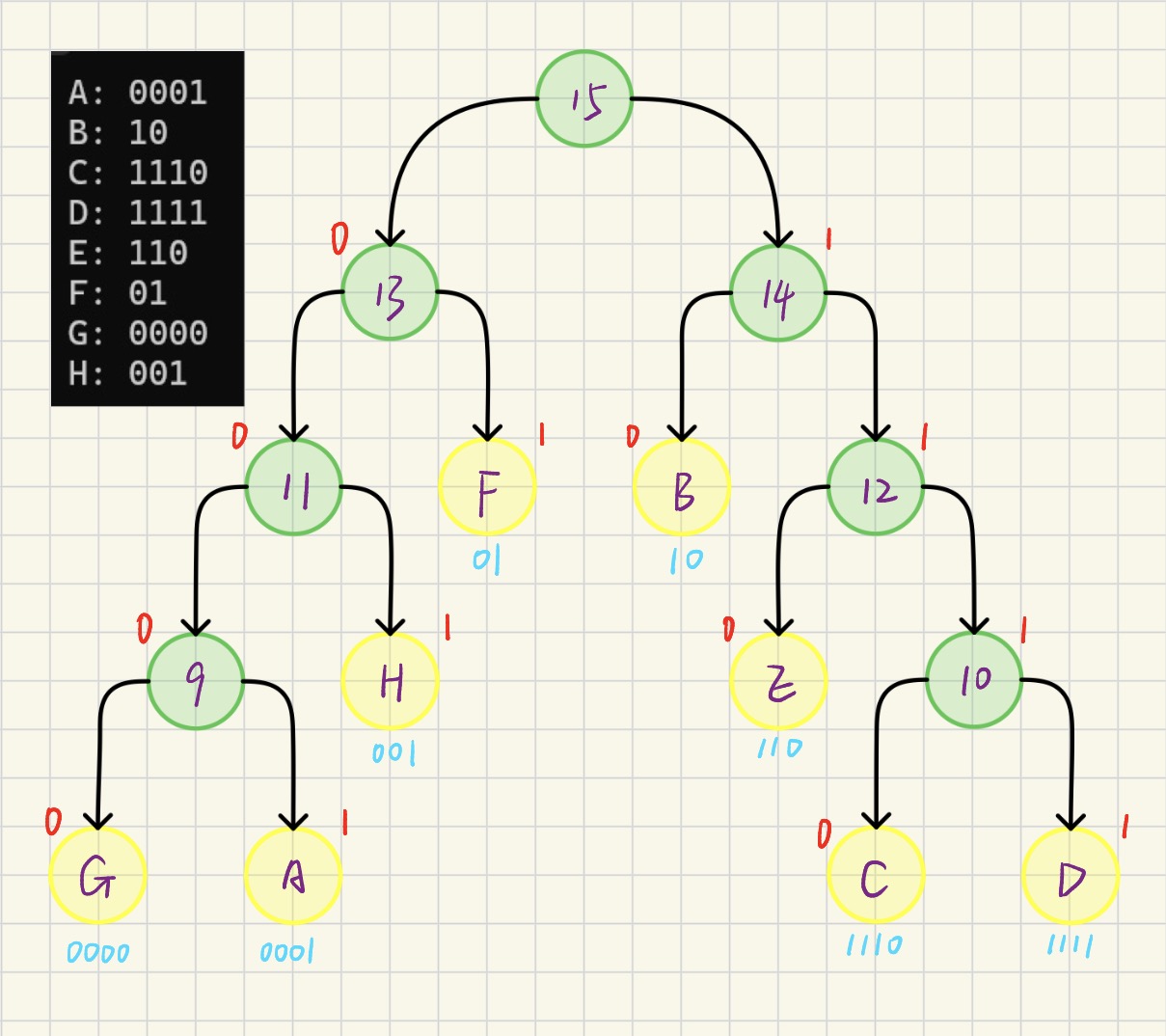
完全正确~

5. 哈夫曼树的内存释放

最后补上内存释放接口就大功告成啦~

void releaseHuffmanCode(HuffmanCode* codes, int n) {
	// 检查编码表指针是否有效
	if (codes) {
		for (int i = 0; i < n; ++i) {
			// 检查当前编码字符串是否有效
			if (codes[i]) {
				// 释放单个编码字符串的内存
				free(codes[i]);
			}
		}
		// 释放编码表数组本身的内存
		free(codes);
	}
}

6. 小结

通过完整的代码实现，我们看到了哈夫曼树从数据结构定义到具体构建，再到编码生成的完整过程。从HuffmanNode的结构体设计，到createHuffmanTree中自底向上的构建策略，再到createHuffmanCode中巧妙的逆向编码生成，每一步都体现了算法设计的精妙之处。特别是selectNode函数中寻找最小权值节点的策略，以及编码生成时从叶子节点回溯到根节点的路径记录，都是哈夫曼编码能够实现最优压缩的关键所在

同时哈夫曼编码的价值不仅在于其压缩效率，更在于它揭示了算法设计的本质智慧：用简单的规则解决复杂的问题。每次选择最小权值节点的贪心策略，看似只关注局部最优，却能通过数学证明达到全局最优。 这种"以小见大"的思想，正是算法设计的精髓所在~

不知道大家掌握了树形结构在数据编码中的各方面应用后，是否会自然地思考：​如果节点间的连接关系更加自由、复杂，不再是严格的父子层次关系，又该如何表示和处理？ 这就引出了图（Graph）这种更为强大的非线性数据结构

图可以看作是树的推广，它能够表示任意对象之间的复杂关系网络。在图中，每个节点（顶点）可以与任意多个其他节点直接相连，形成复杂的网络结构，从而能够建模现实世界中诸如社交网络、交通系统、知识图谱等复杂系统。而从哈夫曼树到图的过渡，正是我们从处理层次化数据到处理网络化数据的必经之路~

回望这些天树的数据结构学习，不知道大家收获有多少呢？树的数据结构就要先告一段落了，接下来，我们就将正式步入图的学习啦~