线性代数 - LU分解(LU-Factorization、LU Decomposition)
flyfish
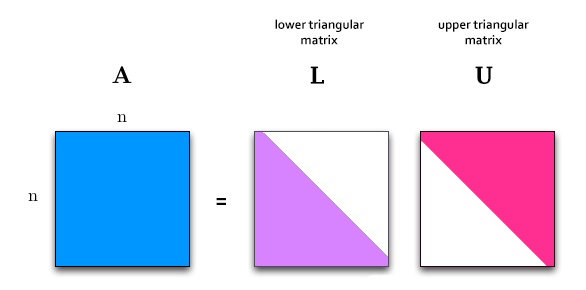
LU分解是把一个方阵拆成一个下三角矩阵(L)和一个上三角矩阵(U)的乘积,满足A = LU。
若能将线性方程组Ax=bAx = bAx=b的系数矩阵AAA分解为A=LUA = LUA=LU(其中LLL和UUU为形式特殊的矩阵),把Ax=b转化为Ly=b和Ux=y,则该方程组可快速求解。
LU 是 Lower triangular matrix(下三角矩阵)和 Upper triangular matrix(上三角矩阵)
Decomposition(分解)
Factorization(因式分解/分解)
LU-Factorization与LU Decomposition同义,Decomposition 和 Factorization 可视为"矩阵分解"的同义词
a11a12a13a21a22a23a31a32a33\]=\[l1100l21l220l31l32l33\]\[u11u12u130u22u2300u33\].\\begin{bmatrix} a_{11} \& a_{12} \& a_{13} \\\\ a_{21} \& a_{22} \& a_{23} \\\\ a_{31} \& a_{32} \& a_{33} \\end{bmatrix} = \\begin{bmatrix} l_{11} \& 0 \& 0 \\\\ l_{21} \& l_{22} \& 0 \\\\ l_{31} \& l_{32} \& l_{33} \\end{bmatrix} \\begin{bmatrix} u_{11} \& u_{12} \& u_{13} \\\\ 0 \& u_{22} \& u_{23} \\\\ 0 \& 0 \& u_{33} \\end{bmatrix}. a11a21a31a12a22a32a13a23a33 = l11l21l310l22l3200l33 u1100u12u220u13u23u33 . #### 三角矩阵 对于方阵,若A=\[aij\]A = \[a_{ij}\]A=\[aij\]为m×nm×nm×n矩阵,则元素a11,a22,a33,...a_{11}, a_{22}, a_{33}, \\dotsa11,a22,a33,...构成AAA的主对角线。若主对角线左下方的所有元素均为0,则称AAA为**上三角矩阵** 。所有行阶梯矩阵均为上三角矩阵。 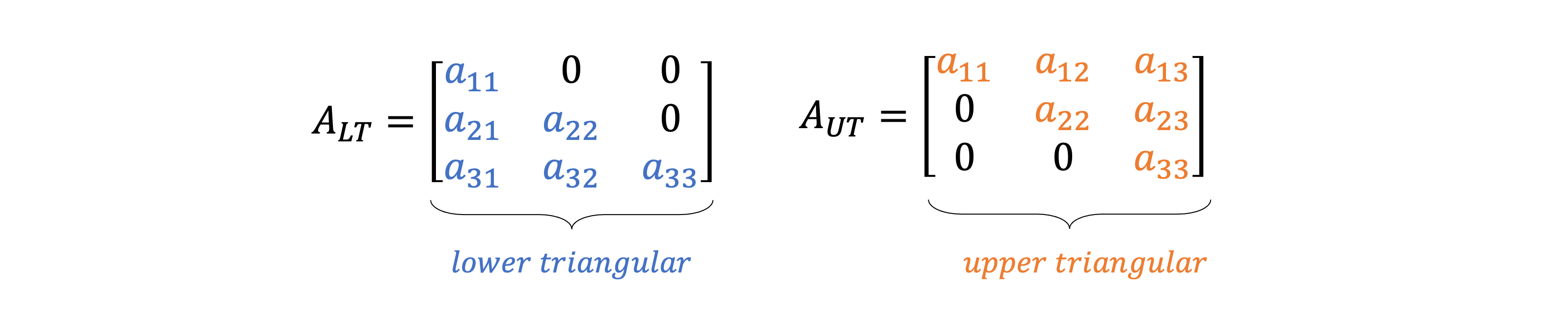例如: \[1−103021100−30\]\[021050003100101\]\[1110−11000000\] \\left\[\\begin{array}{rrrr} 1 \& -1 \& 0 \& 3 \\\\ 0 \& 2 \& 1 \& 1 \\\\ 0 \& 0 \& -3 \& 0 \\end{array}\\right\] \\quad \\left\[\\begin{array}{lllll} 0 \& 2 \& 1 \& 0 \& 5 \\\\ 0 \& 0 \& 0 \& 3 \& 1 \\\\ 0 \& 0 \& 1 \& 0 \& 1 \\end{array}\\right\] \\quad \\left\[\\begin{array}{rrrr} 1 \& 1 \& 1 \\\\ 0 \& -1 \& 1 \\\\ 0 \& 0 \& 0 \\\\ 0 \& 0 \& 0 \\end{array}\\right\] 100−12001−3310 000200101030511 10001−1001100 类似地,若矩阵AAA的转置为上三角矩阵(即主对角线右上方的所有元素均为0),则称AAA为**下三角矩阵** 。上三角矩阵或下三角矩阵统称为**三角矩阵**。 recursive leading-row-column LU algorithm" 递归主行列 LU 算法、分块递归算法 ### 例子 求矩阵A=\[5−51005−33221−220−101−11025\]A = \\begin{bmatrix} 5 \& -5 \& 10 \& 0 \& 5 \\\\ -3 \& 3 \& 2 \& 2 \& 1 \\\\ -2 \& 2 \& 0 \& -1 \& 0 \\\\ 1 \& -1 \& 10 \& 2 \& 5 \\end{bmatrix}A= 5−3−21−532−110201002−125105 的LU分解。 **解** :将AAA化为行阶梯矩阵UUU的过程如下: \[5−51005−33221−220−101−11025\]→\[1−120100824004−1200824\]→\[1−12010011412000−2000000\]=U \\begin{aligned} \\begin{bmatrix} 5 \& -5 \& 10 \& 0 \& 5 \\\\ -3 \& 3 \& 2 \& 2 \& 1 \\\\ -2 \& 2 \& 0 \& -1 \& 0 \\\\ 1 \& -1 \& 10 \& 2 \& 5 \\end{bmatrix} \&\\to \\begin{bmatrix} 1 \& -1 \& 2 \& 0 \& 1 \\\\ 0 \& 0 \& 8 \& 2 \& 4 \\\\ 0 \& 0 \& 4 \& -1 \& 2 \\\\ 0 \& 0 \& 8 \& 2 \& 4 \\end{bmatrix} \\\\ \&\\to \\begin{bmatrix} 1 \& -1 \& 2 \& 0 \& 1 \\\\ 0 \& 0 \& 1 \& \\frac{1}{4} \& \\frac{1}{2} \\\\ 0 \& 0 \& 0 \& -2 \& 0 \\\\ 0 \& 0 \& 0 \& 0 \& 0 \\end{bmatrix} = U \\end{aligned} 5−3−21−532−110201002−125105 → 1000−1000284802−121424 → 1000−10002100041−2012100 =U 则A=LUA = LUA=LU,其中: L=\[5000−3800−24−201801\] L = \\begin{bmatrix} 5 \& 0 \& 0 \& 0 \\\\ -3 \& 8 \& 0 \& 0 \\\\ -2 \& 4 \& -2 \& 0 \\\\ 1 \& 8 \& 0 \& 1 \\end{bmatrix} L= 5−3−21084800−200001 ##### 例子 求可逆矩阵A=\[242112−102\]A = \\begin{bmatrix} 2 \& 4 \& 2 \\\\ 1 \& 1 \& 2 \\\\ -1 \& 0 \& 2 \\end{bmatrix}A= 21−1410222 的LU分解(UUU中无零行)。 **解** :将AAA化为行阶梯矩阵UUU的过程如下: \[242112−102\]→\[1210−11023\]→\[12101−1005\]→\[12101−1001\]=U \\begin{bmatrix} 2 \& 4 \& 2 \\\\ 1 \& 1 \& 2 \\\\ -1 \& 0 \& 2 \\end{bmatrix} \\to \\begin{bmatrix} 1 \& 2 \& 1 \\\\ 0 \& -1 \& 1 \\\\ 0 \& 2 \& 3 \\end{bmatrix} \\to \\begin{bmatrix} 1 \& 2 \& 1 \\\\ 0 \& 1 \& -1 \\\\ 0 \& 0 \& 5 \\end{bmatrix} \\to \\begin{bmatrix} 1 \& 2 \& 1 \\\\ 0 \& 1 \& -1 \\\\ 0 \& 0 \& 1 \\end{bmatrix} = U 21−1410222 → 1002−12113 → 1002101−15 → 1002101−11 =U 则A=LUA = LUA=LU,其中: L=\[2001−10−125\] L = \\begin{bmatrix} 2 \& 0 \& 0 \\\\ 1 \& -1 \& 0 \\\\ -1 \& 2 \& 5 \\end{bmatrix} L= 21−10−12005