算法学习入门---前缀和（C++)

1.写在前面

一维二维模板在leetcode前缀和那边

2.洛谷---最大子段和

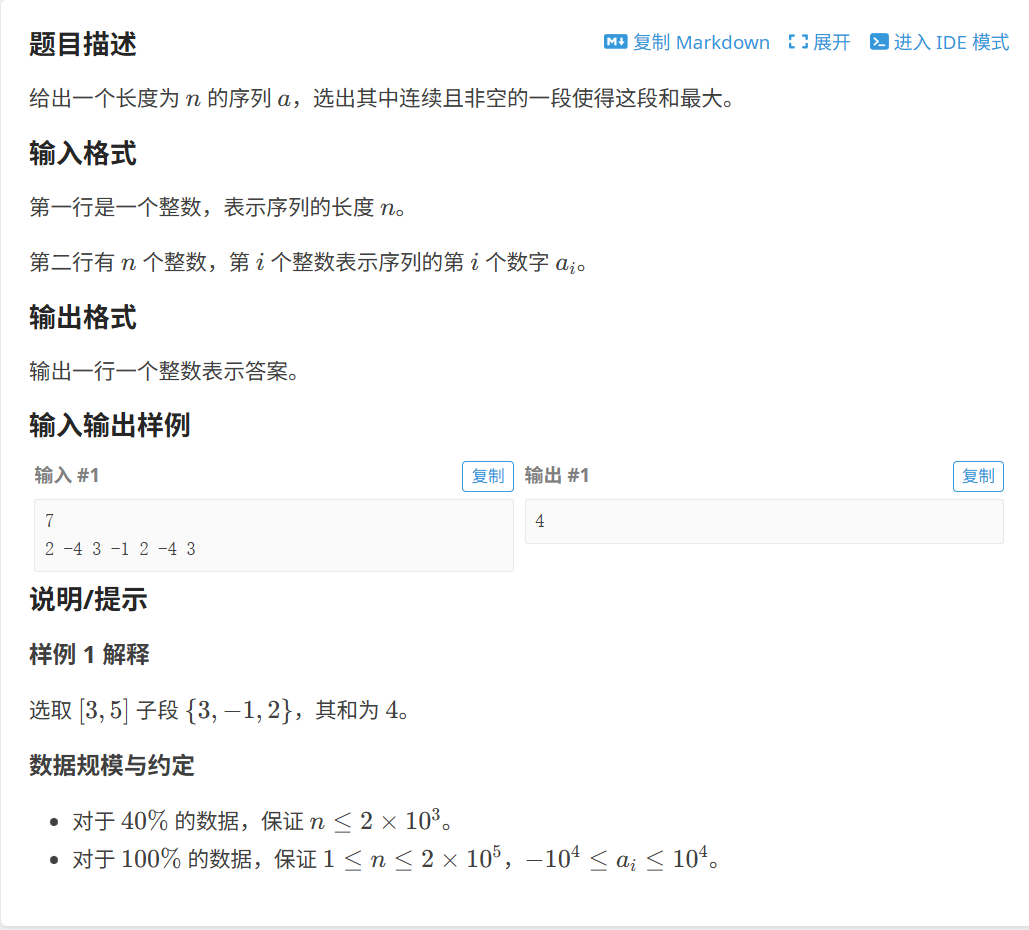
找出一个元素相和最大的子数组，输出元素相和后的结果

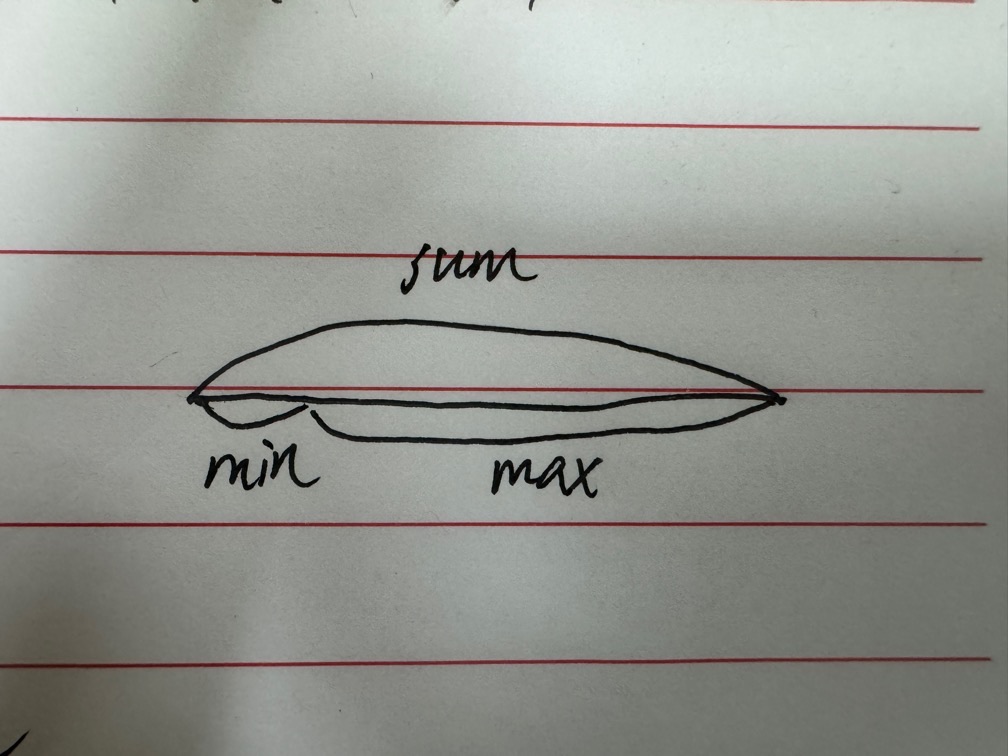
如下图所示，把 $0,i$ 位置处所有的元素相加起来得出sum，再找到这一段区间从头到尾的最小值min，sum - min = max

通过sum变量来模拟dp数组，而不是真的创建一个数组，dp $i$ 为从 0 -> i 位置的所有元素和，dp $i$ = dp $i-1$ + nums $i$ -> sum = sum + nums $i$

cpp 复制代码

#include<iostream>
#include<vector>
#include<algorithm>
#include<limits.h>
using namespace std;


int main()
{
	int n;
	cin>>n;
	vector<int> nums(n,0);
	for(int i=0;i<=n-1;i++) cin>>nums[i];
	int sum = 0,ret = INT_MIN,dp_min = 0;
	for(int x:nums)
	{
		sum+=x;//dp[i] = dp[i-1] + nums[i]
        ret = max(sum-dp_min,ret);
		dp_min = min(sum,dp_min);
	}
	cout<<ret;
	return 0;
}

代码易错点：

dp_min 需要初始化为0，dp_min 是作为保存前缀和最小值的存在，当极限情况时（例如所有的数都是正数），前缀和min的最小值应该为0（即min的那部分被去掉了）

要先更新ret结果，然后再更新dp_min，倒过来会产生结果偏差，例如全是负数的情况

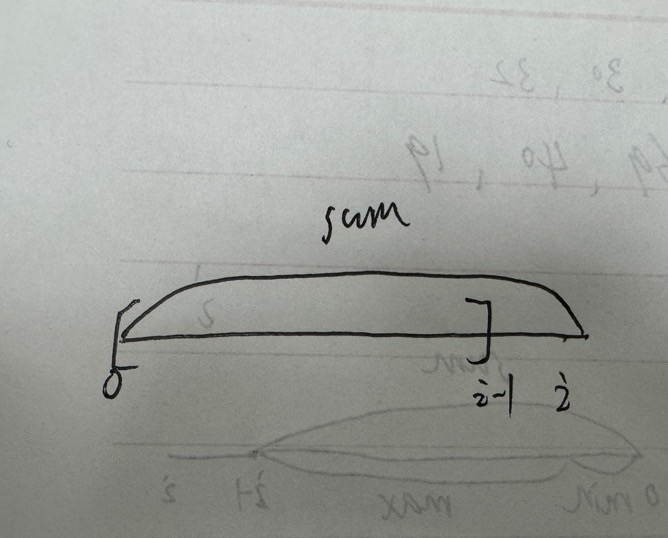
dp_min 一直被 sum 更新，sum - dp_min 也就恒为 0；换成图来理解的话（如下图），sum 统计的是 0->i 区间，dp_min 应该是 $0,i-1$ 区间的前缀和，如果变成 $0,i$ 区间了那就什么也没留下了；如果先更新dp_min再更新ret就是dp_min也被更新为了 $0,i$ 区间，所以是错误的

3.洛谷---激光炸弹

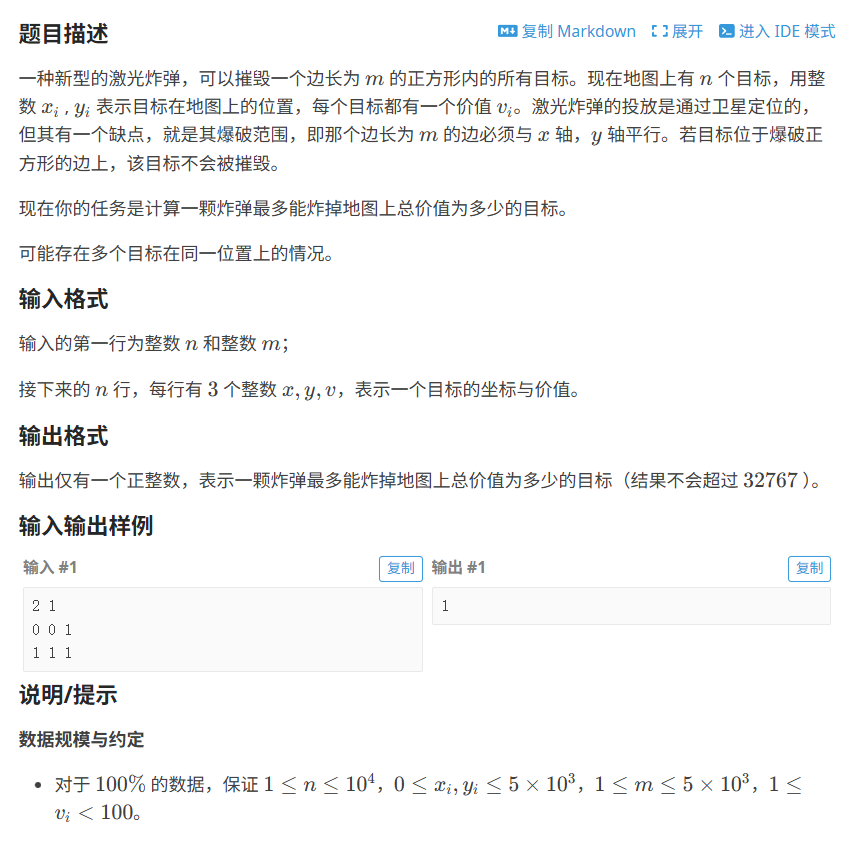
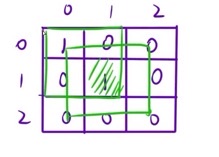
以下图为例，m = 2 时如果想尽可能多的摧毁目标，炸弹的边应该和矩阵的边重合

二维模板：

1.f $i$ $j$ = f $i-1$ $j$ + f $i$ $j-1$ - f $i-1$ $j-1$ + a $i$ $j$

2.sum = f $x2$ $y2$ - f $x1-1$ $y2$ - f $x2$ $y1-1$ + f $x1-1$ $y1-1$

3.x1、x2、y1、y2表示：

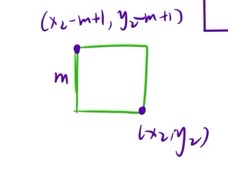
如下图所示，通过 x2，y2 （右下角端点）来遍历整个数组，那么左上角的另一端点为 $x2 - m + 1, y2 -m + 1$

4.细节问题：

前缀和数组下标从1开始算

因为题目的输入没有给出具体的二维数组起止点，因此就直接开辟以最大值作为边长的数组（maxlen = 5 × 10^3）

可能存在同一位置上有多个目标的情况，因此不能 a $x$ $y$ = v，要 a $x$ $y$ += v

代码：

cpp 复制代码

#include<iostream>

using namespace std;

const int N = 5010;

int n,m;
int a[N][N];
int f[N][N];

int main()
{
	cin>>n>>m;
	while(n--)//总共有n组数据
	{
		int x,y,v;
		cin>>x>>y>>v;
		x++,y++;
		a[x][y] += v;
	} 
	//创建前缀和数组
	n = 5001; 
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + a[i][j];
	
	//使用前缀和数组判断出最优解，枚举所有边长为m的正方形 
	int ret = 0;
	for(int x2=m;x2<=n;x2++)
		for(int y2=m;y2<=n;y2++)
			{
				int x1 = x2 - m + 1,y1 = y2 - m + 1;
				ret = max(ret,f[x2][y2] - f[x1-1][y2] - f[x2][y1-1] + f[x1-1][y1-1]);
			} 
	cout<<ret;
	return 0;
}