机器学习-聚类

一.k-means算法

k均值聚类算法是一种迭代求解算法，一般采用常见的欧氏距离作为样本距离度量准则。

每个样本点到本簇中心的距离的平方和也称为误差平方和(SSE)

1.k-means流程

(1).初始化聚类中心：从所有数据点中，随机选择k个不重复的点作为初始的k个聚类中心（k需提前指定）。

(2).分配数据点：计算每个数据点到k个聚类中心的距离（常用欧氏距离），将该点分配到距离最近的聚类中心所在的簇

(3).更新聚类中心：针对每个簇，计算簇内所有数据点的均值（即各维度坐标的平均值），将这个均值作为该簇新的聚类中心。

(4). 判断迭代终止：重复步骤2和步骤3，直到聚类中心的位置变化小于预设的阈值（如移动距离极小），或迭代次数达到设定上限，算法停止。

例子:用k-means算法将下面九个点聚类为两个簇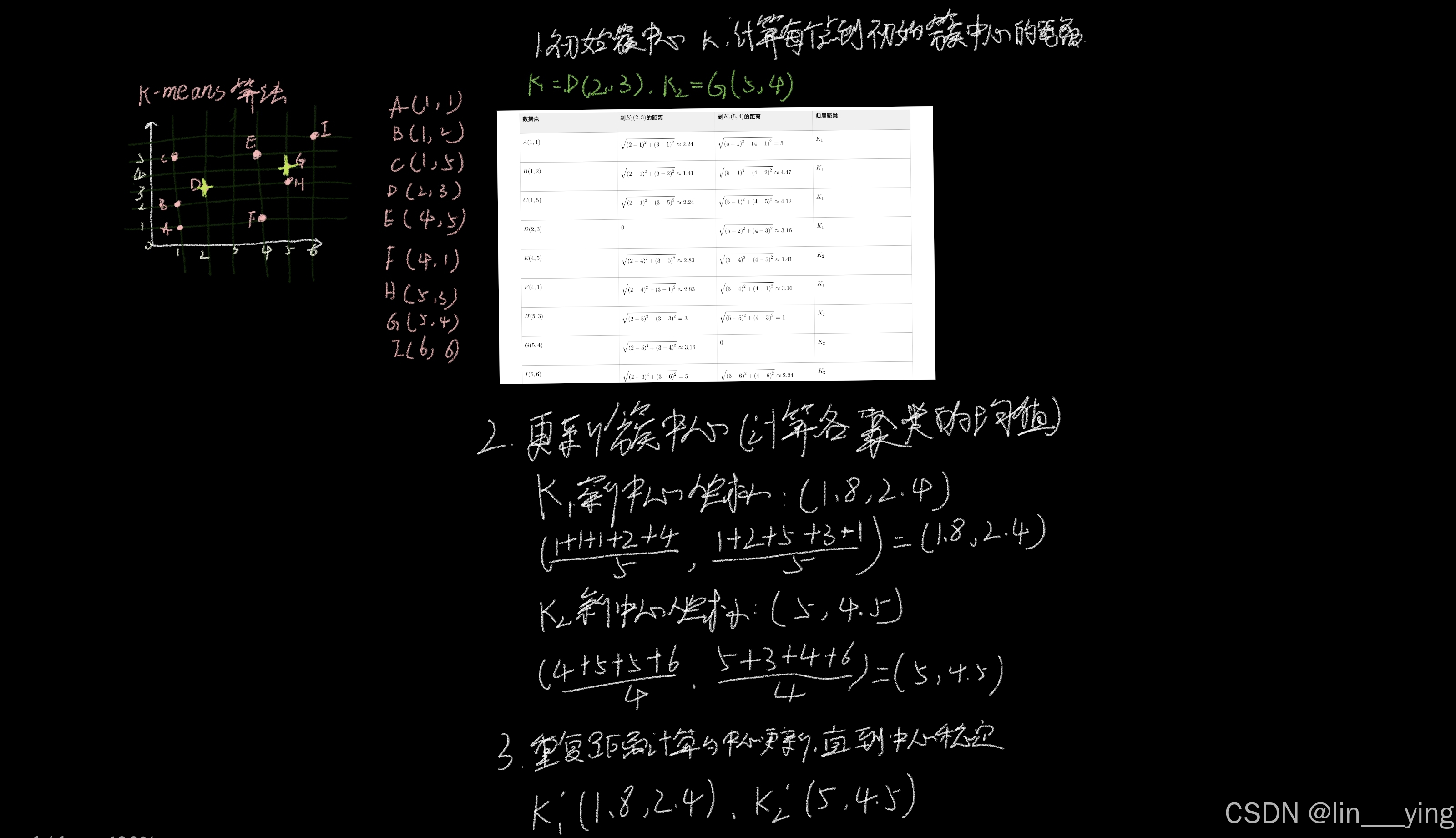

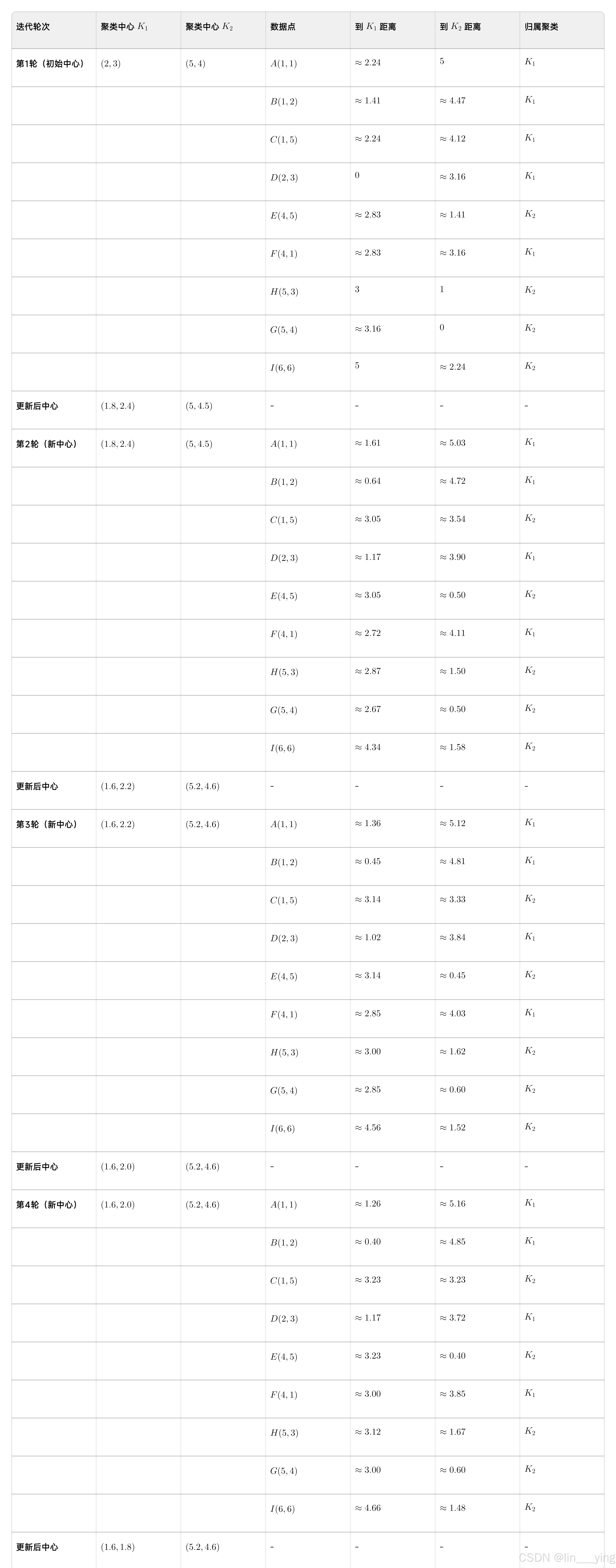
最终稳定的聚类为K1:ABDF K2:CEHGI

2.用python实现k-means算法

KMeans.py

# -*- coding: utf-8 -*-
"""
Created on Thu
k-means clustering algorithm
@author:zzy

"""

import numpy as np
import matplotlib.pyplot as plt


def L2(vecXi,vecXj):
    '''
    计算欧氏距离
    param vecXi:
    param vecXj:
    return:
    '''
    return np.sqrt(np.sum(np.power(vecXi -vecXj,2)))

def kMeans(S,k,distMeans=L2):
    '''
    k均值聚类
    param S:
    param K:
    param distMeans:
    return SSE:误差平方和
    '''

    m = np.shape(S)[0]
    sampleTag = np.zeros(m)

    n = np.shape(S)[1]
    clusterCents = np.array([[-1.93964824,2.33260803],[7.79822795,6.72621783],[10.64183154,0.20088133]])



    sampleTagChanged = True
    SSE = 0.0
    while sampleTagChanged:
        sampleTagChanged = False
        SSE = 0.0

        for i in range(m):
            minD = np.inf
            minIndex = -1
            
            for j in range(k):
                d = distMeans(clusterCents[j,:],S[i,:])
                if d < minD:
                    minD = d
                    minIndex = j
            if sampleTag[i] != minIndex:
                sampleTagChanged = True
            sampleTag[i] = minIndex
            SSE += minD**2
        print(clusterCents)
        plt.scatter(clusterCents[:,0].tolist(),clusterCents[:,1].tolist(),c='r',marker='^',linewidths=7)
        plt.scatter(S[:,0],S[:,1],c=sampleTag,linewidths=np.power(sampleTag+0.5,2))
        plt.show()
        print(SSE)

        #重新计算簇中心
        for i in range(k):
            ClustI = S[np.nonzero(sampleTag[:]==i)[0]]
            clusterCents[i,:] = np.mean(ClustI,axis=0)
    return clusterCents,sampleTag,SSE




if __name__=='__main__':
    samples = np.loadtxt(r"D:\360MoveData\Users\Administrator.DESKTOP-E5JRNOM\Desktop\jqxx\kmeansSamples.txt")
    clusterCents, sampleTag,SSE = kMeans(samples,3)
    plt.show()
    print(clusterCents)
    print(SSE)

kmeansSamples.txt

8.764743691132109049e+00 1.497536962729086341e+01 4.545778445909218313e+00 7.394332431706460262e+00 5.661841772908352333e+00 1.045327224311696668e+01 6.020055532521467967e+00 1.860759073162559929e+01 1.256729723000295529e+01 5.506569916803323750e+00 4.186942275051188211e+00 1.402615035721461290e+01 5.726706075832996845e+00 8.375613974148174989e+00 4.099899279500291094e+00 1.444273323355928795e+01 2.257178930021525254e+00 1.977895587652345855e+00 4.669135451288612515e+00 7.717803834787531070e-01 8.121947597697801058e+00 7.976212807755792555e-01 7.972277764807800260e-02 -1.938666197338206221e+00 8.370047062442882435e+00 1.077781799178707622e+01 6.680973199869320922e+00 1.553118858170866545e+01 5.991946943553537963e+00 1.657732863976965021e+01 5.641990155271871643e+00 1.554671013661827672e+01 -2.925147643580102041e+00 1.108844569740028163e+01 4.996949605297930752e+00 1.986732057663068707e+00 3.866584099986317025e+00 -1.752825909916766900e+00 2.626427441224858939e+00 2.208897582166075324e+01 5.656225833870900388e+00 1.477736974879376675e+01 -3.388227926726261607e-01 5.569311423852095544e+00 1.093574481611491223e+01 1.124487205516641275e+01 4.650235760178413003e+00 1.278869502885029341e+01 8.498485127403823114e+00 9.787697108749913610e+00 7.530467091751554598e+00 8.502325665434069535e+00 6.171183705302398792e+00 2.174394049079376856e+01 -9.333949569013078040e-01 1.594142490265068712e+00 -6.377004909329702542e+00 3.463894089865578341e+00 7.135980906743346175e+00 1.417794597480970609e+01

运行得到

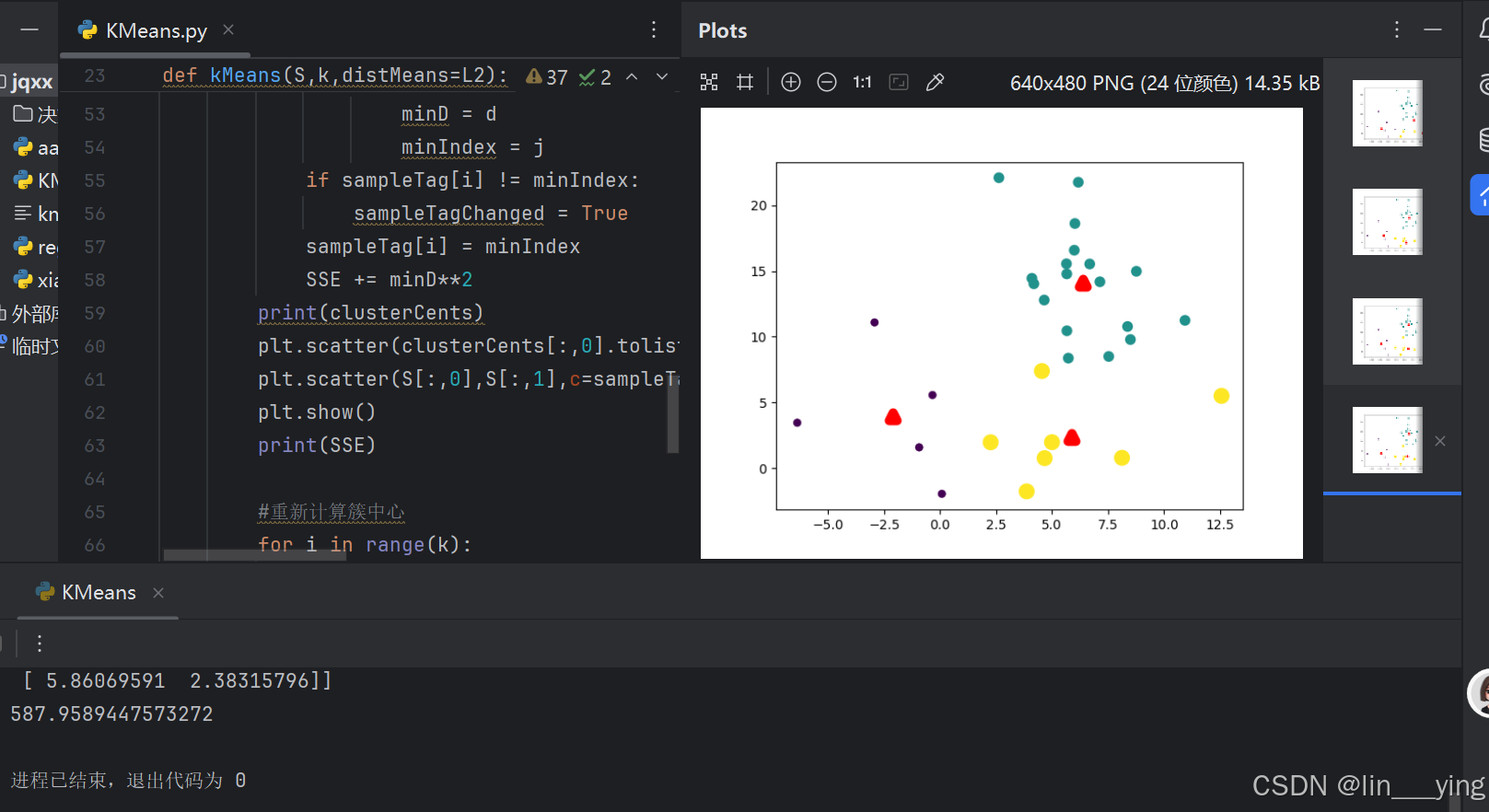
3.k-means算法的优缺点

优点:

(1).计算复杂度低，可解释性强。算法逻辑简单直观，时间复杂度为 O(nkt) （其中 n 是样本数， k 是聚类数， t 是迭代次数），在处理中大规模数据时效率较高，且聚类结果容易理解。

(2).收敛性有保障。只要迭代次数足够，算法能保证收敛到一个局部最优解。

(3).对数值型数据适配性好。适用于连续型数值数据的聚类分析，在许多领域如客户分群、图像分割等场景中应用广泛。

缺点:

(1).需预先指定聚类数 k。实际应用中，用户往往难以提前确定最优的 k 值，若 k 选择不当，会严重影响聚类效果。

(2).对初始聚类中心敏感。不同的初始中心可能导致不同的聚类结果（局部最优而非全局最优），如前面示例中若初始中心选择不同，最终聚类可能有差异。

(3).对非球形簇、不同密度或大小的簇适应性差。仅能识别球形且密度、大小相近的簇，对于不规则形状（如环形、月牙形）或密度差异大的簇，聚类效果不佳。

(4).**对噪声和离群点敏感。**离群点会显著影响聚类中心的计算，导致聚类结果偏离真实分布。

(5).只能处理数值型数据。无法直接处理类别型或混合类型的数据，若要处理这类数据，需先进行数值化转换（如独热编码），但可能引入偏差。

二.改进算法

二分k-means算法试图克服k-means算法收敛于局部最优值的缺陷。核心思路是通过"二分拆分"逐步构建k个聚类

1.二分k-means算法流程

(1). 初始化聚类集合

将所有样本点合并为1个初始聚类，记为聚类集合 C = \{C_1\} （ C_1 包含所有样本）。

​(2). 计算初始SSE

计算当前聚类集合中每个聚类的误差平方和（SSE），总SSE为各聚类SSE之和。

SSE定义：聚类内所有样本到该聚类中心的欧氏距离的平方和

​(3). 迭代拆分聚类

循环执行以下步骤，直到聚类集合的大小等于目标 k ：

选择待拆分的聚类：从当前聚类集合 C 中，选择SSE最大的聚类（记为 C_i ）------因为SSE大意味着该聚类内部样本差异大，更适合拆分。

拆分选中的聚类：对 C_i 执行普通K-means（k=2），得到2个子聚类 C_{i1} 和 C_{i2} 。

更新聚类集合：从 C 中移除 C_i ，加入 C_{i1} 和 C_{i2} 。

更新总SSE：重新计算新聚类集合的总SSE（若总SSE降低，说明拆分有效）。

​(4). 输出结果

当聚类集合的大小达到 k 时，停止迭代，输出最终的 k 个聚类。

2.k-means++算法流程

K-Means++的核心是通过"距离加权概率"选择初始中心

(1).随机选1个样本作为第一个聚类中心，避免完全无方向的初始化。

(2).计算每个样本到"已选中心"的最短距离（d(x,\mu)），衡量样本与现有中心的分散程度。

(3).用距离的平方（D(x)^2）作为权重计算选择概率（P(x)），距离越远的样本被选中的概率越高，保证初始中心的分散性。

(4).重复步骤2-3，直到选够k个初始中心，后续流程与普通K-Means一致。

3.k-medoids算法

k--medoids算法与k--means算法不同之处在于簇中心的计算方式不同。k-means：簇中心是虚拟的"均值点"，由簇内所有数据点的特征均值计算得出，该点未必是数据集中的实际样本。k-medoids：簇中心是真实的"代表点"（medoid），从簇内所有实际数据点中选出，其特点是使簇内其他点到它的总距离最小。

k-medoids算法核心是选择实际数据点作为聚类中心（medoid），通过迭代替换中心来最小化簇内数据点到中心的总距离

k--medoids算法流程

(1). 初始化 ：从所有数据点中随机选择k个不重复的点，作为初始medoid（聚类中心）。

​(2).分配簇 ：计算每个非medoid点到所有k个medoid的距离，将该点分配到距离最近的medoid所在的簇。

​(3).尝试替换（Swap） ：对每个簇，依次用簇内的非medoid点（候选点）替换当前medoid，计算替换后簇内的总距离（成本）。

​(4).判断是否更新 ：若替换后的总距离比替换前更小，则保留该候选点为新medoid；否则，维持原medoid不变。

​(5). 迭代终止：重复步骤2-4，直到所有medoid都不再被替换，或达到预设的迭代次数，算法收敛。

4.Mini Batch k-means算法

Mini Batch k-means算法通过略微牺牲优化质量来取得显著减少计算时间的效果。它的基本思路是用随机抽取的代表样本来进行优化计算，而不是在全部样本上进行计算

Mini Batch k--means算法流程

(1). 初始化：随机选k个点作为初始簇中心。

(2). 抽批次：每次从全量数据中取一小部分样本（Mini Batch）。

(3). 更中心：将批次内样本分配到最近簇，用这批样本更新对应簇中心。

(4). 终止：重复2-3，直到簇中心变化极小或迭代次数达标。

三.聚类算法基础

1.聚类任务

聚类任务是无监督学习下的核心任务，核心是让算法自动将无标签数据，按"相似度/距离"分成若干组（簇），最终实现"簇内数据相似、簇间数据差异大"的效果。

2.样本点常用距离度量

(1)Lp距离

Lp距离（Lp Metric）是一类距离的通用表示框架，通过调整参数p的值，可涵盖欧氏距离、曼哈顿距离等常见距离，核心是衡量n维空间中两点的"差异程度"。

其数学定义为:

关键通过p值区分具体距离类型：

当 p=1 时，即曼哈顿距离，计算"直角折线"距离（如城市中沿街道行走的路径）。

当 p=2 时，即欧氏距离，计算"空间直线"距离（如两点间的最短路径）。

当 p→∞ 时，即切比雪夫距离，取两点各维度差值的最大值（如棋盘上国王的一步最大移动距离

(2).VDM距离

VDM距离，即值差异度量（Value Difference Metric），是一种用于衡量离散无序属性之间距离的方法，核心思想是将离散无序的数据转化为可以量化的差异度量，以进行比较和分析。在实际应用中，VDM距离常与闵可夫斯基距离结合，用于处理包含有序属性和无序属性的混合属性数据 。

对于定义域为{飞机,火车,轮船}这样的离散无序属性，不能直接在属性值上计算距离，此时可采用VDM

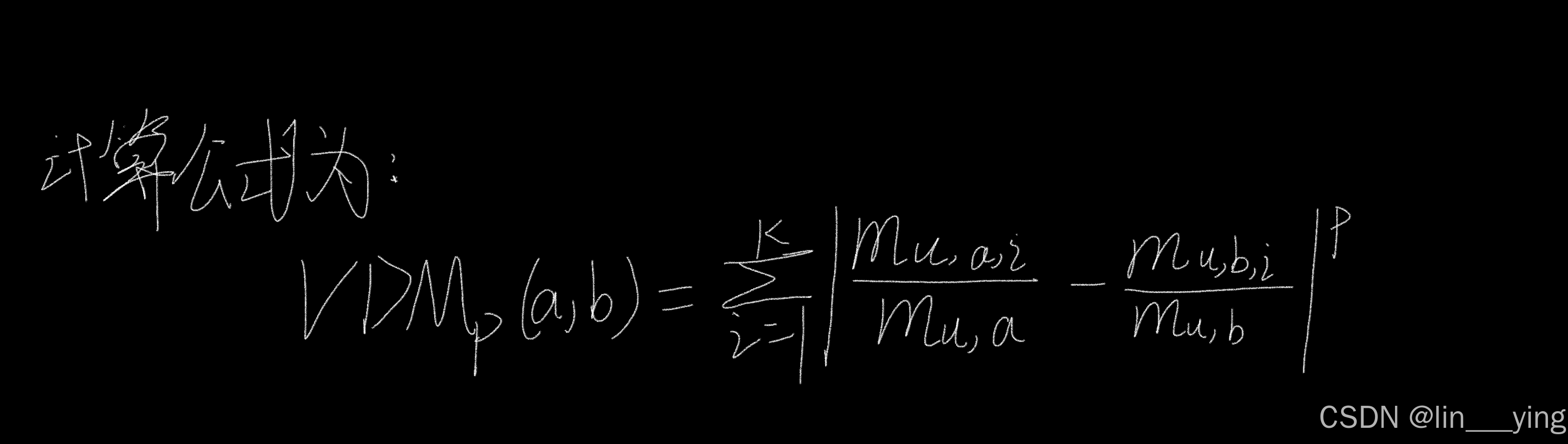
其中，m_{u,a}表示在属性u上取值为a的样本数，m_{u,a,i}表示在第i个样本簇中在属性u上取值为a的样本数，k为样本簇数。

(3).混合加权距离

混合加权距离是一种将多种距离度量方法结合起来，并为每种距离度量分配相应权重，从而计算数据点之间差异的方法，它可以更全面地反映数据点之间的相似性或差异性。

在实际应用中，混合加权距离常用于处理包含多种类型特征的数据。如在基于混合加权距离的KNN心衰患者死亡率评估模型中，就利用值差度量和曼哈顿距离混合计算样本间的距离，以提高模型性能。

(4). 余弦相似度

余弦相似度是衡量两个向量在空间中夹角余弦值的指标，核心用于判断向量方向的相似性，值越接近1表示方向越一致（相似度越高），越接近-1则方向越相反。

3.聚类算法评价指标

1.外部指标

(1).Jaccard系数(JC)

Jaccard系数（JC，又称交并比）是衡量两个集合相似度的指标，核心通过"交集大小与并集大小的比值"量化重合程度，广泛用于聚类、分类、文本匹配等场景。

(2).FM指数(FMI)

FM指数（Fowlkes-Mallows Index，FMI）是一种用于聚类结果外部评价的指标，核心通过"精确率"与"召回率"的几何平均，量化聚类分组与真实标签的匹配程度。

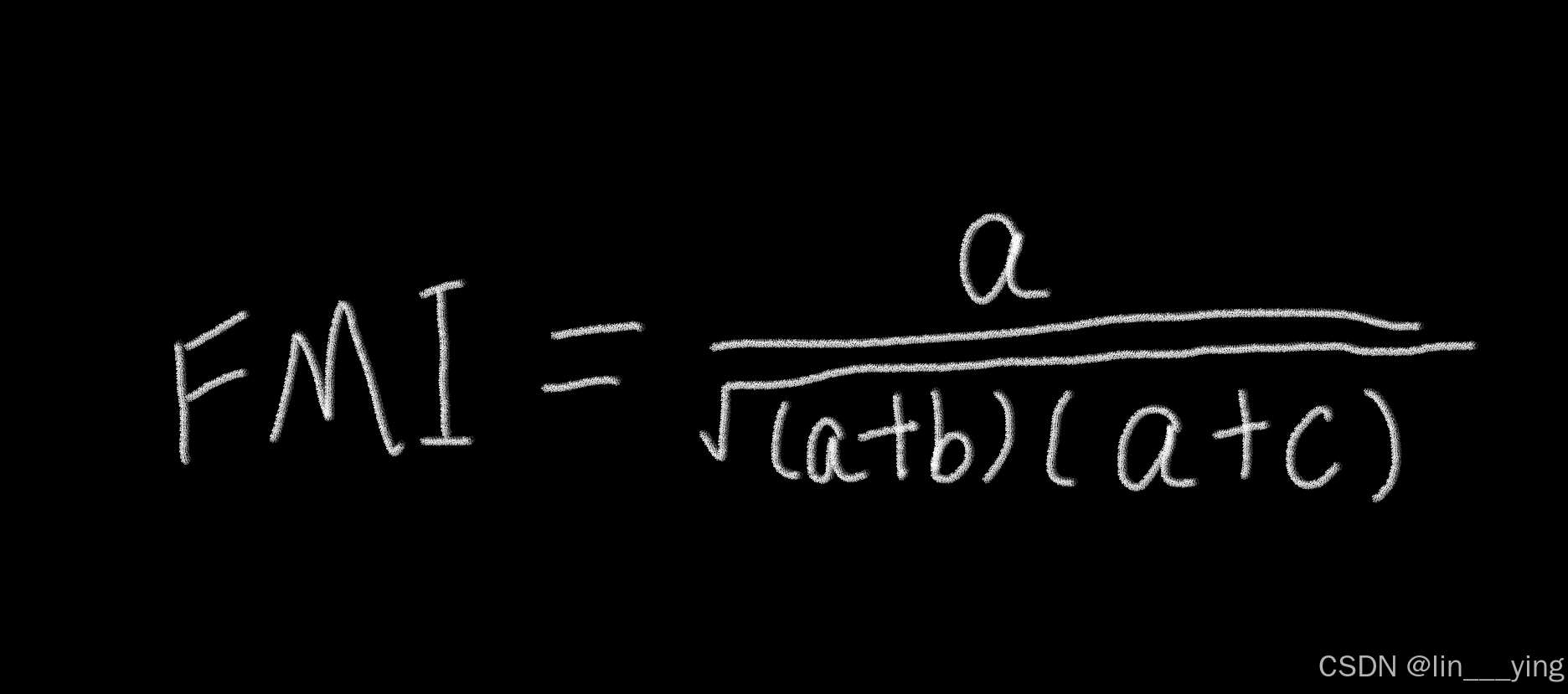
其中,a+b是出现在同一预先分组中样本对数,a+c是出现在同一算法分簇中的样本对数。该指数取值于0~1,值越大,算法分簇与预先分组越接近,值越小,算法分簇与预先分组越不相关。

2.内部指标

若某聚类算法给出的分簇C＝{C1，C2，C3，...，Ck},定义

(1) 样本xm与同簇Ci其他样本的距离:

该距离也称为xm的簇内平均不相似度

(2) 样本xm与 不同簇Cj内样本的平均距离:

该距离也称为xm与簇Cj的平均不相似度

(3).样本Xm与簇的最小平均距离:

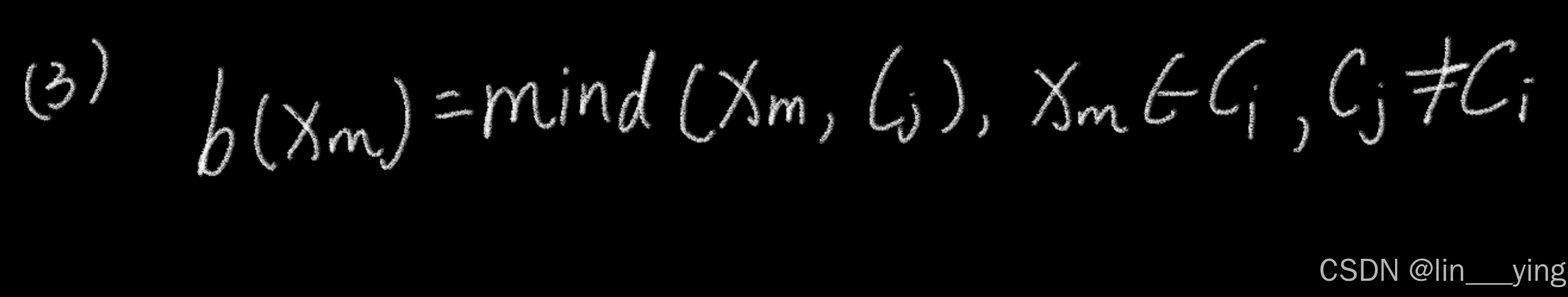
该距离是取xm与所有其他不同簇的平均距离中的最小值

(4).簇内样本平均距离:

(5).簇内样本最大距离:

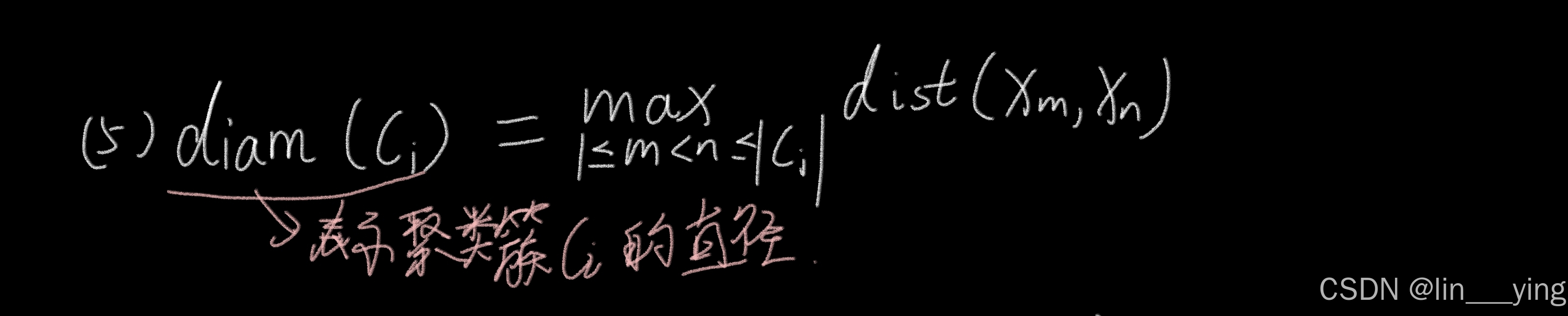
(6).簇最小距离:

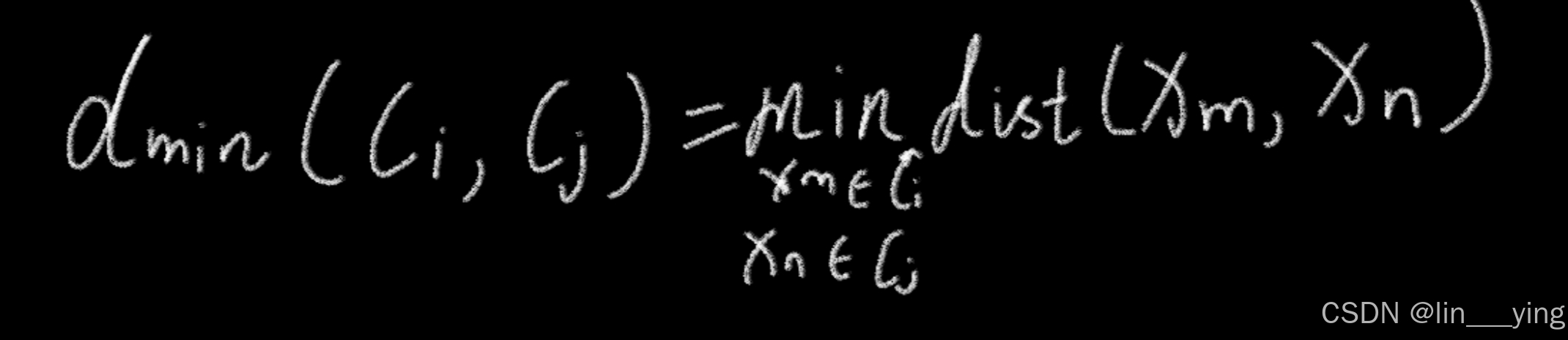
(7).簇中心距离:

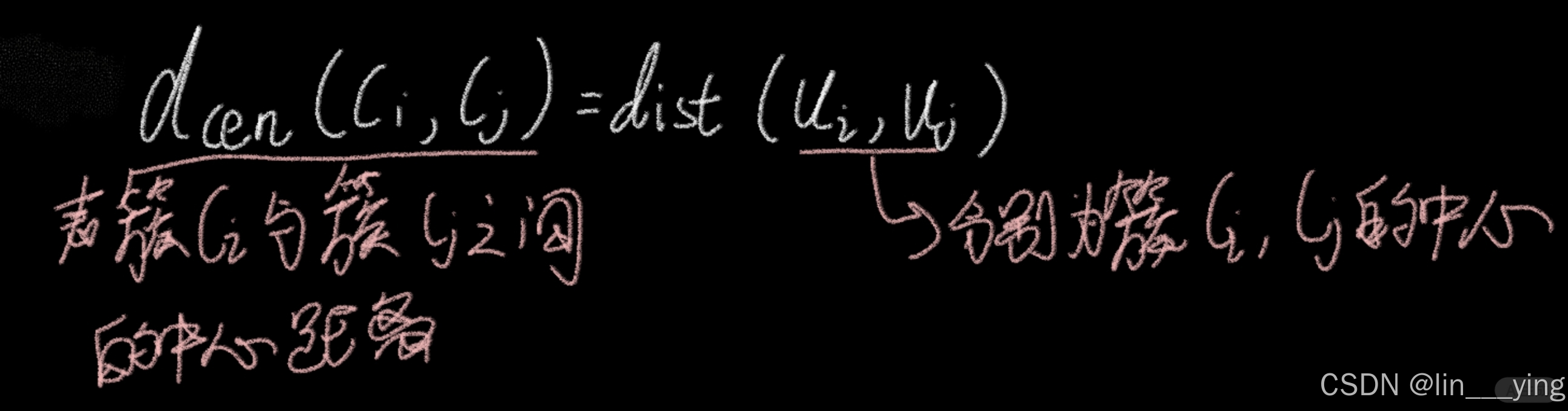
根据以上距离，可定义以下内部评价指标

(1)轮廓系数(SC)

单一样本xm的轮廓系数为:

一般使用的轮廓系数是对所有样本的轮廓系数取均值。CS值高表示簇内密集，簇间疏散。

(2).DB指数(DBI)

DB指数，即Davies-Bouldin Index，是一种用于评估聚类算法性能的内部指标。

它基于簇内的紧密性和簇间的分离性来衡量聚类的质量，其值越小，说明聚类效果越好。

(3).Dunn指数(DI)

Dunn指数（DI）是评估聚类效果的指标，通过计算"类间最小距离"与"类内最大直径"的比值，取各聚类对应值的最小值。其核心逻辑是衡量类间分离度与类内紧致度，数值越大代表聚类结果越优，适用于K-means等算法的结果评估。

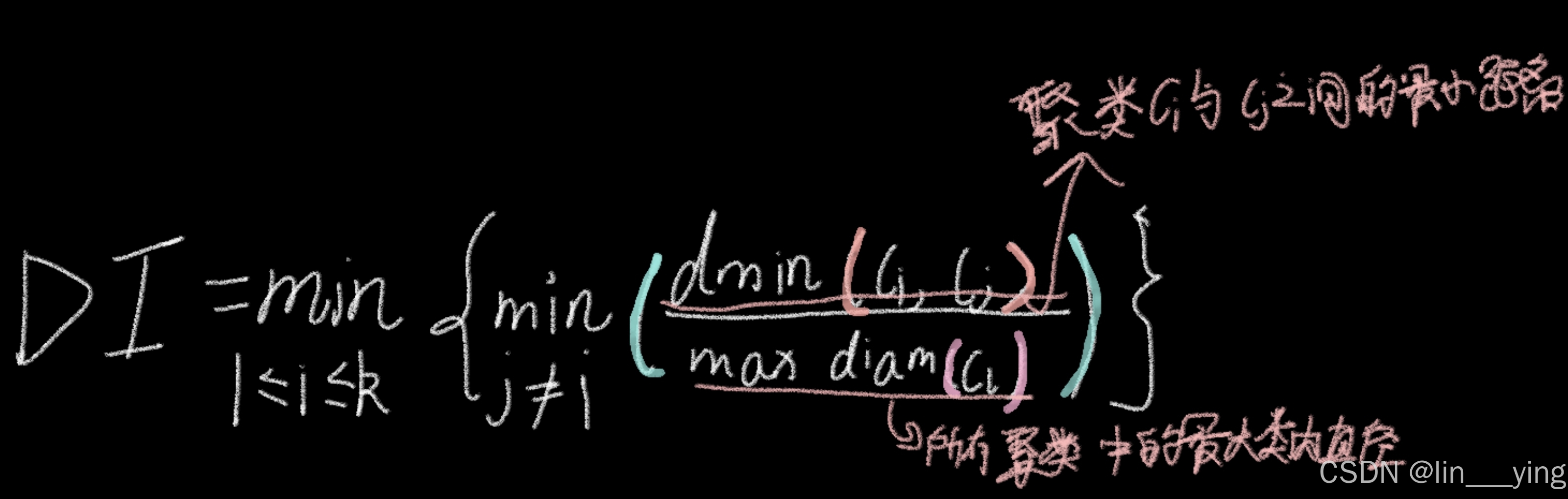
4. 聚类算法分类

(1).划分聚类

核心：将数据划分为预设数量的簇，通过迭代优化簇内相似度。

典型算法：K-means（基于距离的簇中心更新）、K-medoids（抗噪声，用实际样本点作中心）

(2).密度聚类

核心：基于样本密度划分簇，能发现任意形状的簇，自动识别噪声。

典型算法：DBSCAN（通过ε邻域和最小点数定义核心点）、OPTICS（优化DBSCAN的参数敏感性）

(3).层次聚类

核心：通过"凝聚（从单个样本开始合并）"或"分裂（从全样本开始拆分）"生成聚类树。

代表算法：AGNES（凝聚式）、DIANA（分裂式）。

(4).网络聚类

核心：依赖网络拓扑结构（而非节点属性)，需同时考虑节点连接的"密度""权重""方向"（如无向/有

向图）；部分场景会结合节点属性（如用户画像）优化聚类效果。

典型算法：GN算法（Girvan-Newman）、Louvain算法

(5).模型聚类

核心:基于概率模型或生成模型的聚类方法

典型算法:高斯混合模型（Gaussian Mixture Model, GMM)、贝叶斯高斯混合模型（Bayesian Gaussian Mixture Model）、隐马尔可夫模型（Hidden Markov Model, HMM)

四.DBSCAN及其派生算法

DBSCAN是经典的密度聚类算法

1.密度相关概念

(1).ε-邻域

对于数据集中的任意样本点 p ，以 p 为中心、以预设距离阈值ε 为半径的区域内，所有包含的样本点的集合，称为 p 的 ε-邻域，记为 Nε(p)

ε是DBSCAN算法需要指定的两个参数之一

(2).核心点和边界点

核心点：DBSCAN中，若点的ε-邻域内样本数≥预设最小点数阈值MinPts，该点为核心点，是聚类扩展的基础

边界点：自身非核心点，但落在某核心点的ε-邻域内，属于聚类却不驱动聚类生长

简而言之，核心点是"高密度核心"，边界点是"核心周围的低密度边缘"，二者共同构成DBSCAN的聚类结构

(3).直接密度可达

若点q在核心点p的ε-邻域内，且p是核心点（ε-邻域样本数≥MinPts），则q从p直接密度可达，是密度关系的"直接连接"

(4).密度可达

若存在点链p→p₁→p₂→...→q，每相邻两点直接密度可达，且p是核心点，则q从p密度可达，体现"传递性"，是单向关系

(5).密度相连

若存在核心点o，点p和q均从o密度可达，则p与q密度相连，是双向关系，同一聚类内的点彼此密度相连。

2.DBSCAN算法流程

1. 设定核心参数 ：确定两个关键参数------ε（epsilon，邻域半径） 和 MinPts（邻域内最少样本数），这是算法的基础

​

2. 识别核心点 ：遍历所有样本点，若某点邻域（以该点为中心、ε为半径）内的样本数 ≥ MinPts，则标记为核心点；反之则为非核心点

​

3. 扩展密度簇 ：从任意未分类的核心点出发，将其所有直接/间接密度可达的样本（通过核心点连接的点）归为同一簇，并标记簇内所有点

​

4. 标记噪声点：遍历完所有核心点后，剩余未被任何簇包含的非核心点，即为噪声点（异常值）

3.OPTICS算法

OPTICS（Ordering Points To Identify the Clustering Structure）算法是一种基于密度的聚类算法，它可以看作是DBSCAN算法的扩展。与DBSCAN直接输出聚类结果不同，OPTICS通过计算样本点的可达距离（reachability distance）和核心距离（core distance），生成一个有序的点序列和对应的可达距离图，从而帮助用户识别不同密度的聚类结构

1. 核心距离（Core Distance）：对于给定的参数 min_samples ，样本点成为核心点所需的最小距离（即第 min_samples 个最近邻的距离）。若样本点不是核心点，则核心距离未定义

2. 可达距离（Reachability Distance）：从核心点 p 到点 q 的可达距离，定义为 max(核心距离(p), 距离(p, q)) 。若 p 不是核心点，则可达距离未定义

OPTICS算法流程

1. 初始化所有点为"未处理"状态

2. 遍历每个未处理的点 p ：

​ ▪ p 是核心点，计算其所有 ε 邻域内的点，生成一个有序的种子列表（按可达距离排序）。

​▪从种子列表中选取可达距离最小的点 q ，标记为"已处理"，并将其加入结果序列。

​▪若 q 是核心点，计算其邻域内点相对于 q 的可达距离，更新种子列表。

​3. 重复步骤2，直到所有点都被处理，生成最终的有序序列和可达距离

4.AGNES算法

(1).簇之间的距离变量

①簇最小距离

簇最小距离是两个簇成员之间的最小距离

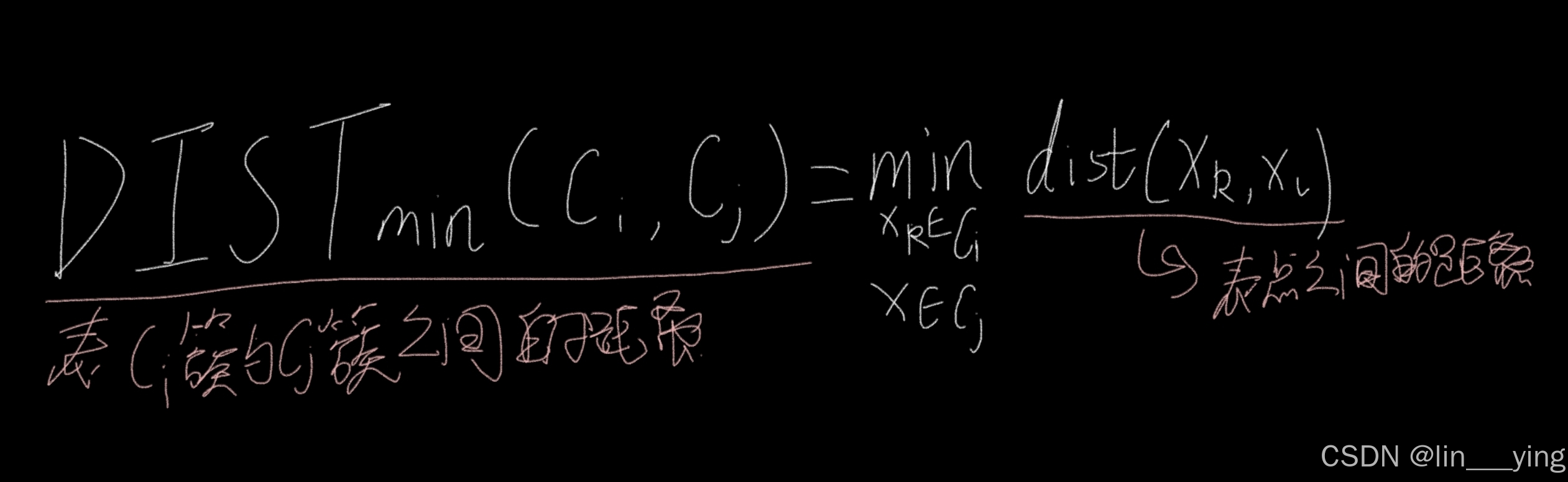
②簇最大距离

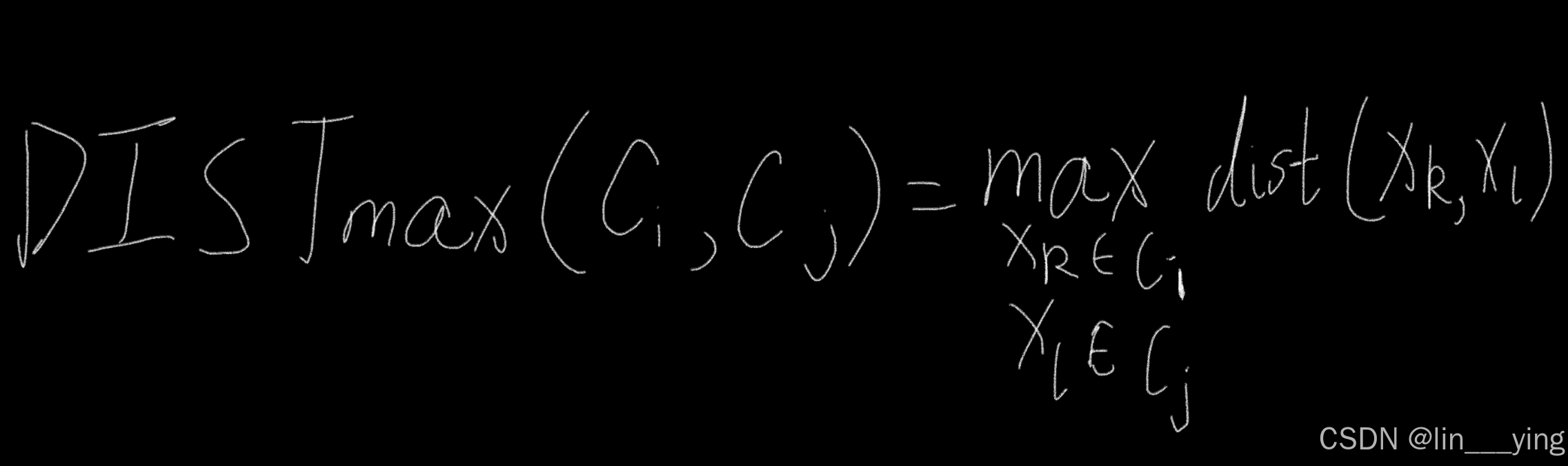
③簇平均距离

簇平均距离是两个簇成员之间距离的平均值

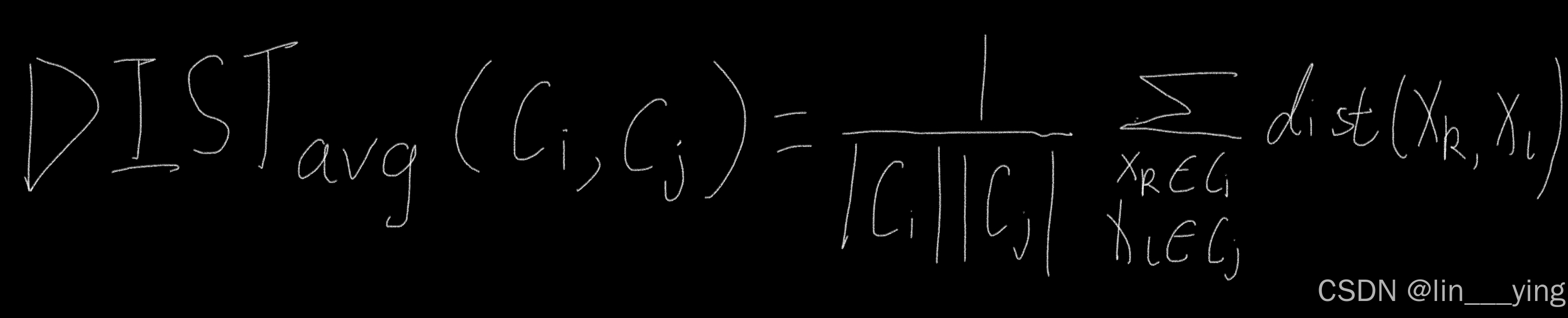
④簇中心距离

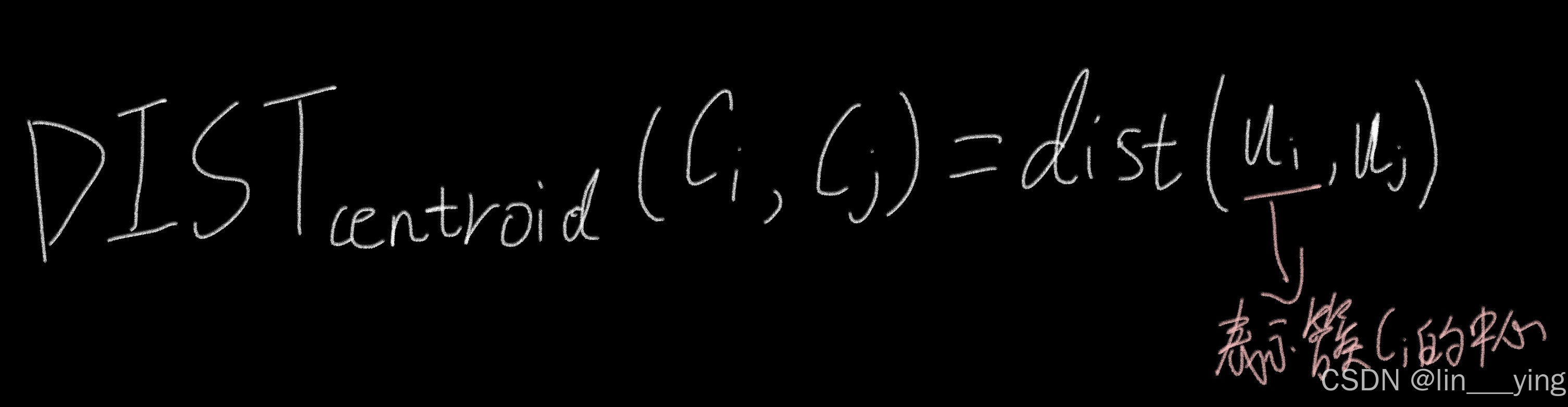
(2).算法流程

AGNES（Agglomerative Nesting）是一种自底向上的层次聚类算法，其核心流程是从每个样本为单个簇开始，不断合并距离最近的簇，直到满足停止条件（如达到预设簇数）

1 .初始化簇

将数据集中的每个样本都视为一个独立的簇，即初始簇的数量等于样本数量 n ，记为 {C1,C2,...,Cn } 。

2.计算簇间距离矩阵

根据选择的簇间距离度量（如单链接、全链接、平均链接、重心距离等），计算所有簇对之间的距离，生成一个 n × n 的距离矩阵。

3.合并距离最近的两个簇

在距离矩阵中找到距离最小的两个簇 Ci 和 Cj ，将它们合并为一个新的簇 Cnew = Ci ∪ Cj 。

4：更新簇集合和距离矩阵

从簇集合中移除 Ci 和 Cj ，并将新簇 Cnew 加入簇集合。

重新计算新簇与所有剩余簇之间的距离，更新距离矩阵。

5.重复合并过程

重复步骤3和步骤4，直到满足停止条件（常见条件：簇的数量达到预设值、簇间最小距离超过某个阈值、所有样本合并为一个簇）。