基于Matlab的递推最小二乘法参数估计

---

### 文章目录

• [@[TOC](文章目录)](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [前言](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [一、批处理法与递推法比较](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [二、递推最小二乘法](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [三、MATLAB实现](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [1.Step1](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [2.Step2](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [3.Step3](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [4.Step4](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [5.Step5andStep6](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [6.Step7](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [7.完整代码](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)
• [四、结果展示](#文章目录 @TOC 前言 一、批处理法与递推法比较 二、递推最小二乘法 三、MATLAB实现 1.Step1 2.Step2 3.Step3 4.Step4 5.Step5andStep6 6.Step7 7.完整代码 四、结果展示)

前言

既上一章的继续学习，延续上一章的风格。

---

一、批处理法与递推法比较

批处理最小二乘法（Batch Least Squares, BLS）和递推最小二乘法（Recursive Least Squares, RLS）是最小二乘估计的两种核心实现方式，核心差异在于数据处理方式（一次性处理所有数据 vs 逐次更新数据），进而导致两者在适用场景、性能、资源占用等方面各有优劣。

这是我通过AI整理的两种方法的优缺点，如下：

简单理解：

批处理最小二乘（BLS）：离线一次性处理全量数据，实现简单、精度高，但内存占用和计算复杂度随数据量增加而升高，无实时性，适合静态系统离线拟合。

递推最小二乘（RLS）：逐次处理新增数据，实时性强、内存占用固定（与数据量无关），能跟踪时变参数，但实现稍复杂、理论上有微小累积误差，适合在线系统、大数据量或时变场景。
核心选择：离线高精度用 BLS，在线 / 时变 / 大数据用 RLS。

二、递推最小二乘法

这里直接给出该方法公式，这个公式可以根据批处理法公式推理过来，推理过程比较复杂，不是我们的学习要求。

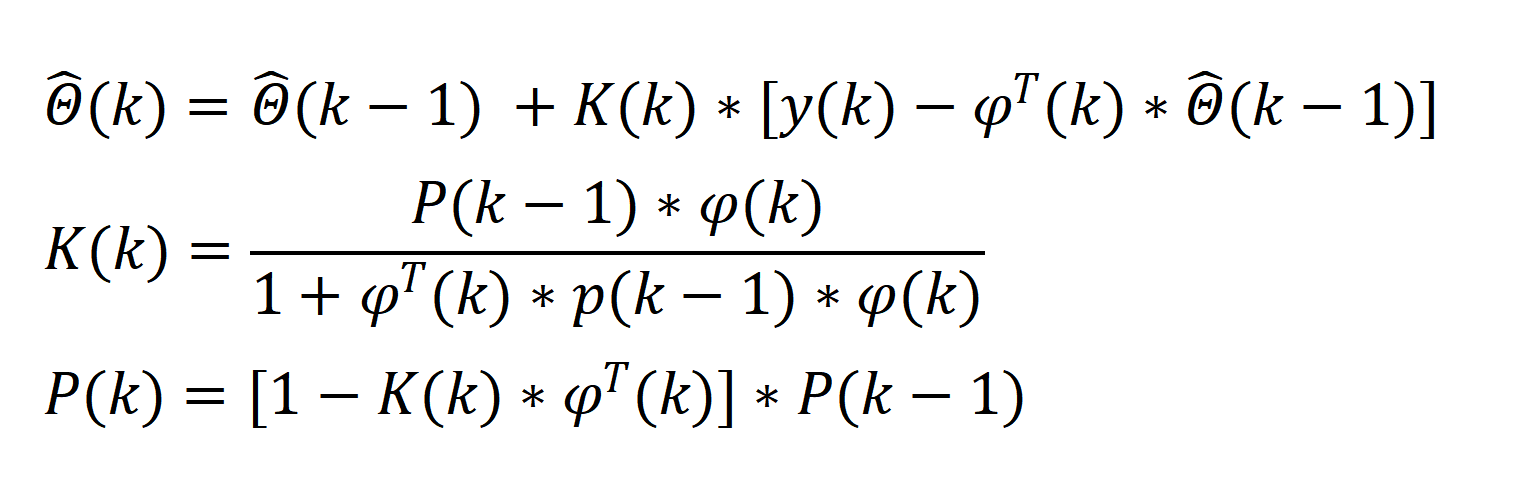
Θ(k)是我们估计的参数，P(k)和K(k)都是中间变量，其中P(0)和Θ(0)定义如下：

接下来还是和上文一样，给定一个具体的系统方程，来验证递推最小二乘法的性能。

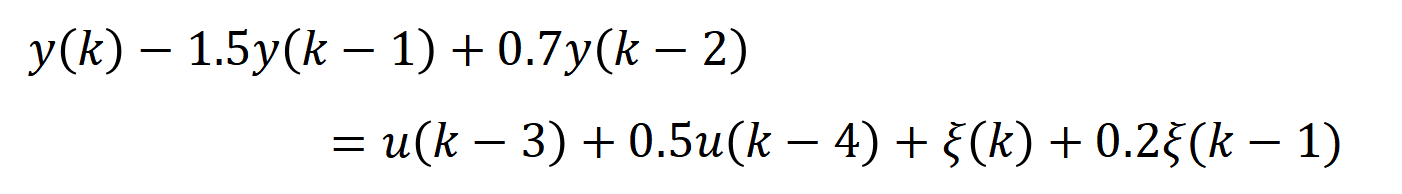
算法步骤：

Step1 表示系统的输入参数矩阵和输出参数矩阵

Step2 确定输入输出矩阵大小、输入信号、噪声信号

Step3 完成其他变量初始化

Step4 实现递推最小二乘法公式

Step5 更新数据

Step6 步进加1，返回Step4，继续循环

Step7 打印结果

三、MATLAB实现

1.Step1

将矩阵整理成以下形式

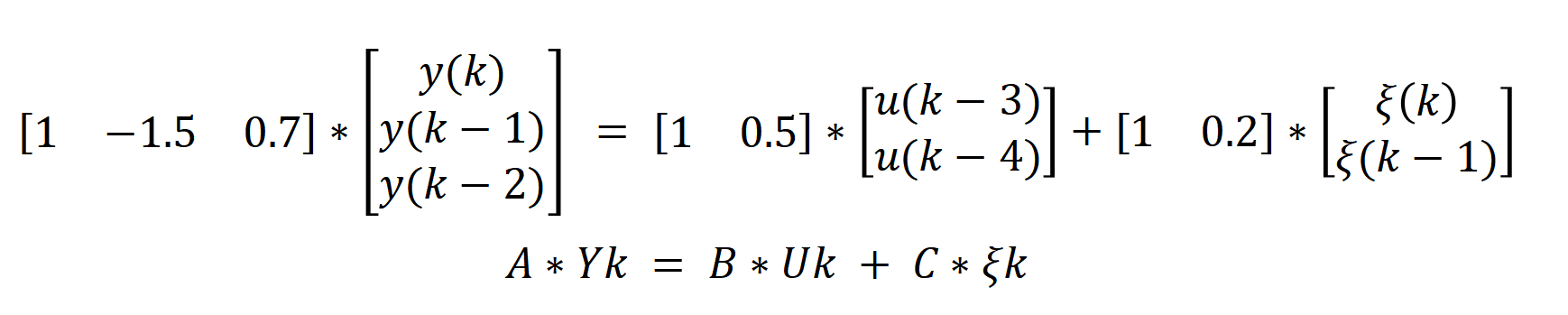
代码实现如下

clear; close all;
A = [1 -1.5 0.7];
B = [1 0.5];
C = [1 0.2];
d = 3;
na = length(A) - 1; %2
nb = length(B) - 1; %1

d、na、nb的含义见往文。

2.Step2

L = 400;
uk = zeros(d+nb, 1);
yk = zeros(na, 1);
u = randn(1,L);
white_noise = sqrt(0.1)*randn(1,L+1);
white_noise(1) = 0;

L就是参数估计次数，uk和yk的表达式如下，元素初始为0

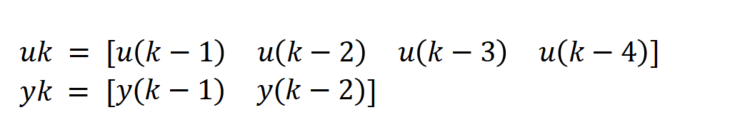
输入信号u设定为正态分布，white_noise 也就是ξ(k)设定为期望为0，方差为0.1的高斯分布。因为方程中有ξ(k-1)项，所以共有L+1项，令white_noise(k) 代表ξ(k-1)；

3.Step3

theta = [A(2:na+1) B]';
thetak_1 = zeros(na+nb+1,1);
thetak = zeros(na+nb+1,L);
P =10^10*eye(na+nb+1);

theta也就是Θ(k)，thetak用来记录估计的k时刻Θ参数，thetak_1用来记录估计的k-1时刻Θ参数，保持和theta同类型矩阵，元素初始化为0。P按要求初始化即可

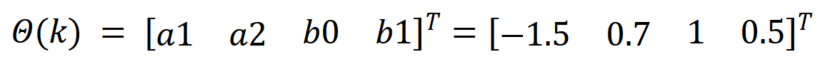
4.Step4

for k = 1:L
    phik = [-yk; uk(d: d+nb)];
    y_now = phik' * theta + white_noise(k+1)+0.2*white_noise(k);
    %递推最小二乘法
    K_now = P * phik / (1+phik'*P*phik);
    thetak(:,k) = thetak_1 + K_now*(y_now - phik'*thetak_1);
    P = (eye(na+nb+1) - K_now*phik')*P;

为了方便求y(k)可以将方程写成如下形式。phik 就是φ(k)。y_now 就是计算的当前输出值，K_now 是当前中间变量K(k)的值，thetak(:,k)用于计算当前参数估计的Θ(k)值，并且所有的值都合并到一个矩阵中，方便后期打印。

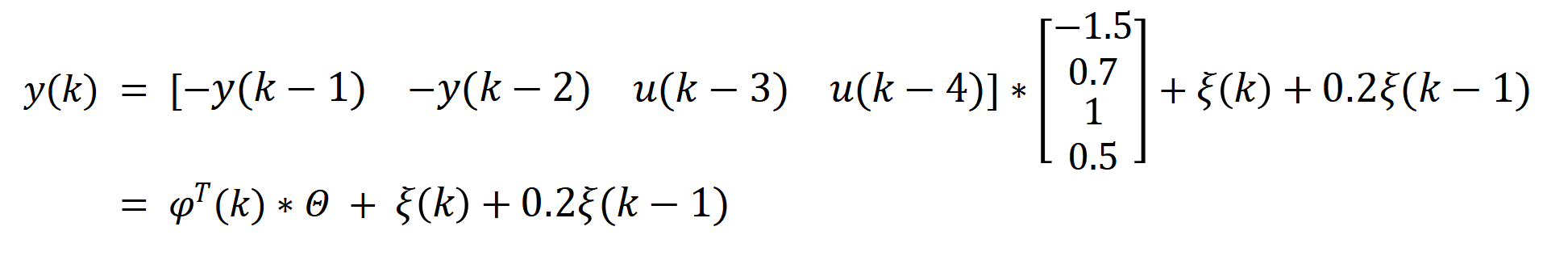
5.Step5andStep6

%更新数据
    thetak_1 = thetak(:,k);
    %输入信号更新begin
    for i = d+nb:-1:2
        uk(i) = uk(i-1);
    end
    uk(1) = u(k);
    %输入信号更新end
    %输出信号更新begin
    for i = na:-1:2
        yk(i) = yk(i-1);
    end
    yk(1) = y_now;
    %输出信号更新end
end

6.Step7

plot(1:L,thetak);
xlabel('k');
ylabel('参数估计a,b');
title('递推最小二乘法仿真')
legend('a_1','a_2','b_0','b_1');
axis([0 L -2 1.5]);

7.完整代码

clear; close all;
A = [1 -1.5 0.7];
B = [1 0.5];
C = [1 0.2];
d = 3;
na = length(A) - 1; %2
nb = length(B) - 1; %1

L = 400;
uk = zeros(d+nb, 1);
yk = zeros(na, 1);
u = randn(1,L);
white_noise = sqrt(0.1)*randn(1,L+1);
white_noise(1) = 0;

theta = [A(2:na+1) B]';
thetak_1 = zeros(na+nb+1,1);
thetak = zeros(na+nb+1,L);
P =10^10*eye(na+nb+1);

for k = 1:L
    phik = [-yk; uk(d: d+nb)];
    y_now = phik' * theta + white_noise(k+1)+0.2*white_noise(k);
    %递推最小二乘法
    K_now = P * phik / (1+phik'*P*phik);
    thetak(:,k) = thetak_1 + K_now*(y_now - phik'*thetak_1);
    P = (eye(na+nb+1) - K_now*phik')*P;
    %更新数据
    thetak_1 = thetak(:,k);
    %输入信号更新begin
    for i = d+nb:-1:2
        uk(i) = uk(i-1);
    end
    uk(1) = u(k);
    %输入信号更新end
    %输出信号更新begin
    for i = na:-1:2
        yk(i) = yk(i-1);
    end
    yk(1) = y_now;
    %输出信号更新end
end
plot(1:L,thetak);
xlabel('k');
ylabel('参数估计a,b');
title('递推最小二乘法仿真')
legend('a_1','a_2','b_0','b_1');
axis([0 L -2 1.5]);

四、结果展示

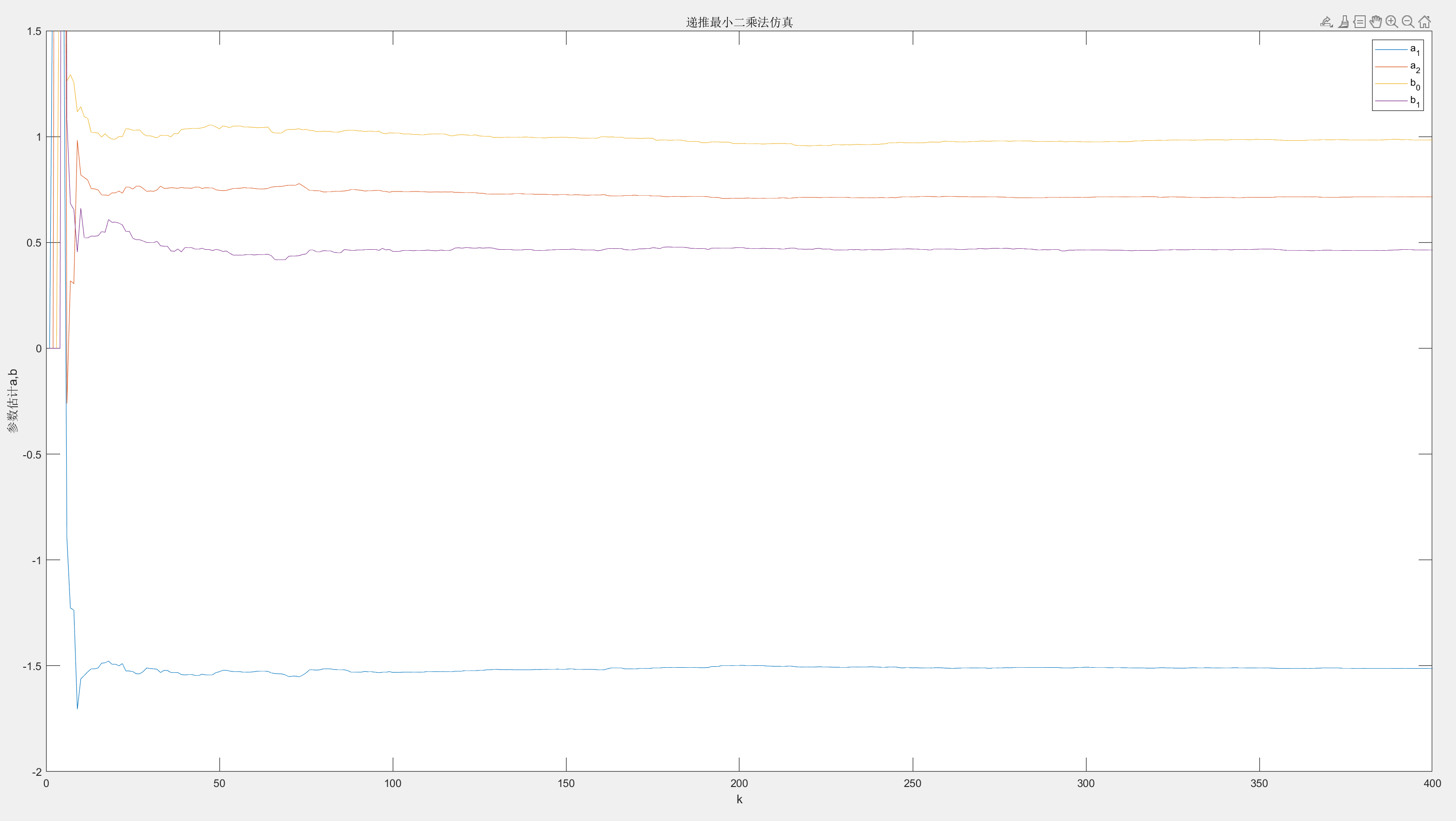
可以看出从25次数据往后估计的值和理论值是非常接近的。去除噪声如下

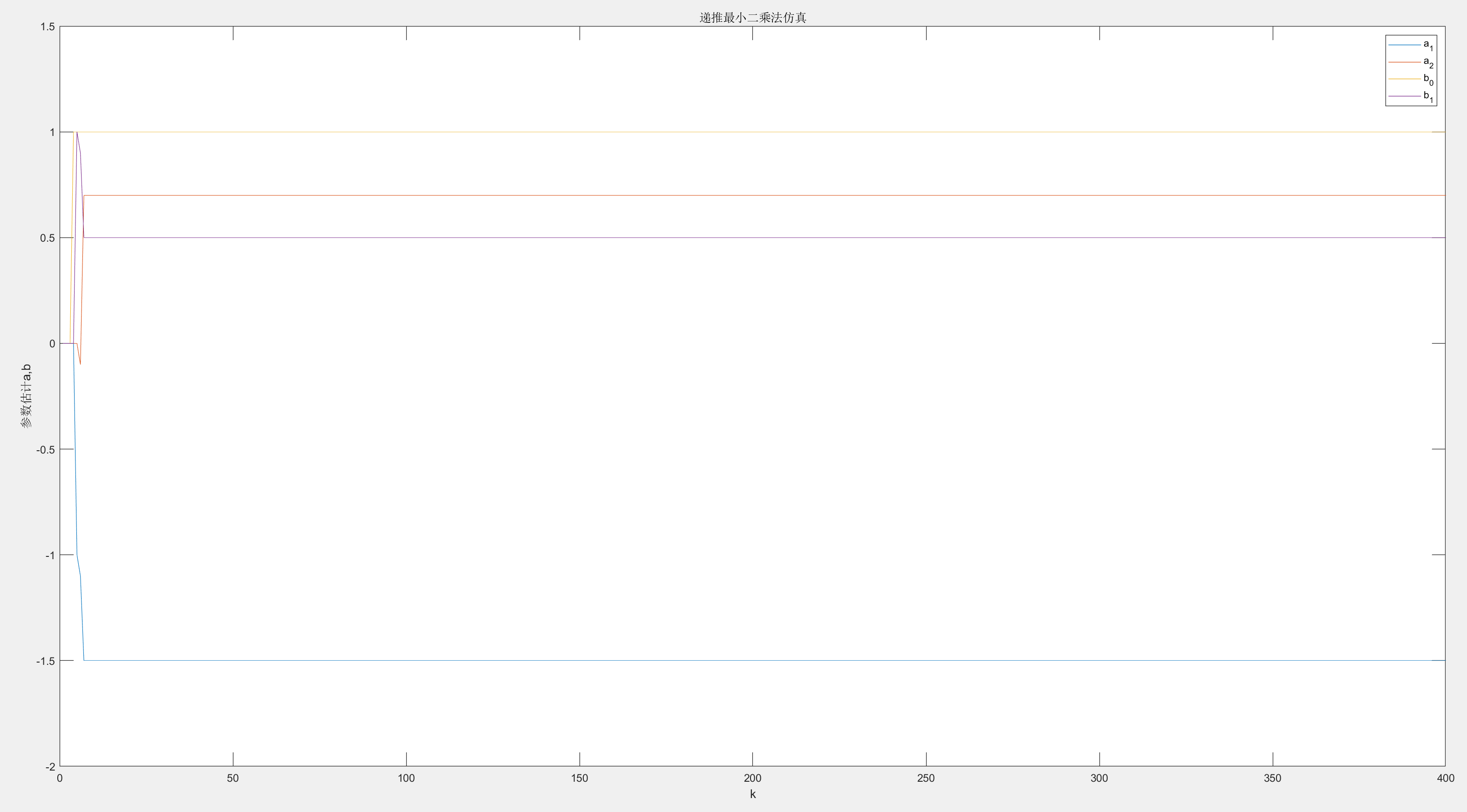
可以看出大约10次左右估计值就完全等于理论值，代表递推法成功。