
程序可作为轨迹约束定位、模型匹配定位以及多假设运动判别问题的基础验证平台,也可进一步与 IMM、粒子滤波或地图约束方法融合,形成更高阶的工程应用方案。
文章目录
代码简述
该代码面向三维空间中的地面目标定位与轨迹判别问题 ,假设目标的真实运动轨迹并非完全未知,而是受限于若干条已知的候选轨迹集合,本MATLAB程序将匹配到的轨迹与GNSS观测到的位置进行融合。
问题建模与基本假设
-
候选轨迹模型
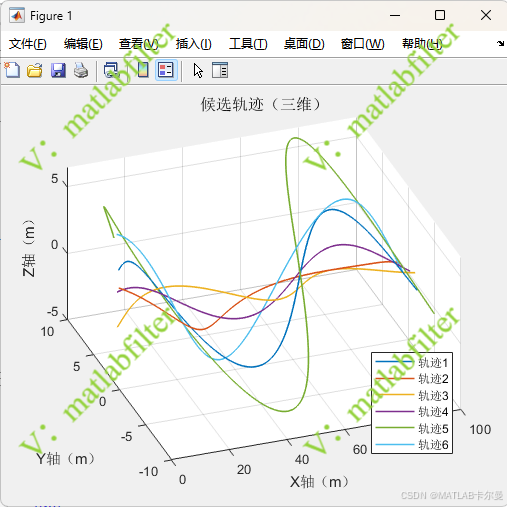
代码首先在三维空间中构造若干条候选真实轨迹,每条轨迹由时间参数化,轨迹数量可任意设置,且各轨迹在空间形态上存在明显差异,用于模拟多种可能的真实运动模式。
-
观测模型
假设目标真实运动严格沿其中某一条轨迹运动,
观测为GNSS,存在随机噪声与偏置,观测模型可抽象表示为
z k = p k true + b + v k \mathbf{z}_k = \mathbf{p}_k^{\text{true}} + \mathbf{b} + \mathbf{v}_k zk=pktrue+b+vk其中 p k true \mathbf{p}_k^{\text{true}} pktrue为真实轨迹位置, b \mathbf{b} b为系统偏置, v k \mathbf{v}_k vk为零均值高斯噪声。
仿真设计与性能评估
代码从多个层面验证所提方法的有效性:
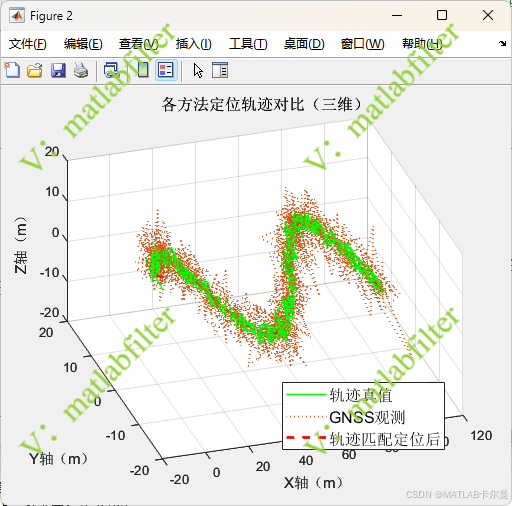
- 三维轨迹对比:直观展示真实轨迹、GNSS 观测轨迹与轨迹匹配后的定位结果
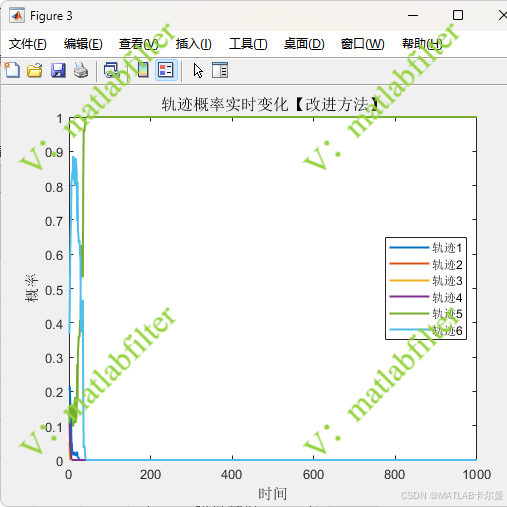
- 轨迹概率演化:给出各候选轨迹概率随时间变化过程,验证累计概率的收敛性
- 误差分析:对比 GNSS 直接观测与轨迹匹配定位后的三轴误差及三维欧氏距离误差
- CDF 统计特性:通过累积分布函数定量评估定位精度提升效果
结果表明,引入轨迹先验并采用累计概率更新后,目标定位误差在三个坐标轴及总体三维距离意义下均得到显著改善,同时轨迹识别结果具有更强的稳定性和一致性。
运行结果
各个轨迹的概率曲线:
各种轨迹的分布:
真实轨迹与估计的轨迹对比:
误差曲线:

MATLAB代码
部分代码如下:
matlab
%% 地面目标,已知其带误差的轨迹、若干条可能的真实轨迹【三维】,用于实时判断对应的轨迹,并定位
% 轨迹数量可任意设置、各轨迹概率实时输出
% 创新性提出基于累计概率的改进方法,并与传统方法进行对比
% 作者V:matlabfilter,接定位与导航、滤波相关的matlab代码定制
% 2026-01-07/Ver1
clear; clc; close all;
rng(0);
%% == 构造若干真实轨迹(三维示例)==
num_tracks = 6; % 轨迹总数量
t = [0.1:0.1:100]';
traj_set = cell(num_tracks,1);% 存储(定义)各个轨迹的单元格数组
for i = 1:num_tracks
% 随机生成不同形状的三维轨迹
x = t;
y = (2*randn+2)*sin(0.1*t + 0.01*i) + i*0.1;
z = (1.5*randn+1)*cos(0.08*t + 0.02*i) + i*0.15; % 新增Z轴
traj_set{i} = [x, y, z];
end
% 初步绘制三维轨迹完整代码下载链接:https://download.csdn.net/download/callmeup/92543495
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者