专栏导读
- 作者简介:工学博士,高级工程师,专注于工业软件算法研究
- 课程1 《有限元编程从入门到精通40讲 》旨在提供 1.以案例 的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码 ;2.单元类型 包含:杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,壳单元,四/六面体实体单元,金字塔单元等;3**.物理场问题** 涉及:力学 、传热学 、电磁学 及多物理场耦合 等问题的稳态 (静力学)和瞬态 (动力学)求解。专栏旨在帮助有志于有限元工业软件开发的小伙伴,快速上手有限元编程,在案例中成长,摆脱按部就班填鸭式教学。
- 视频教程与源码获取地址: https://www.bilibili.com/video/BV1kP4y1d7Zo
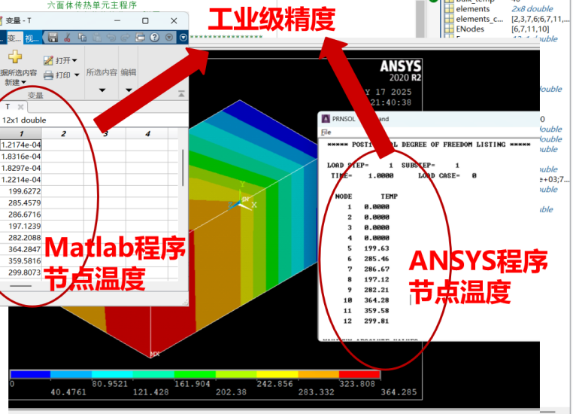
- **课程2《热传导问题Matlab有限元编程 》**MATLAB传热有限元编程专题课,以案例驱动,面向编程实战,计算精度对标ANSYS。随课附赠学习包:【课程讲义】+【案例MATLAB源码】+【案例APDL命令流】+【理论文本】+【30余本经典有限元教材】 【课程内容】: ·2D/3D传热(三角形单元tri3/tri6,四边形单元quad4,四面体单元tet4,六面体单元hex8) ·瞬态热传导有限元方程的直接积分方法。 ·三类边界条件:固定温度边界条件,热流密度边界条件,热对流边界条件,体积热源的施加 ·间接热固耦合:Step1.通过传热单元计算得到温度场;Step2在结构单元施加温度场实现热应力的求解。 ·直接热固耦合单元:实现温度场、结构位移场、机械应变、热应变、总应变场的求解。 ·工业级计算精度:对标软件ANSYS,求解误差<1%
- 视频教程与源码获取地址 : 1. 热传导问题Matlab有限元编程-课程介绍-稳态瞬态传热/热固耦合/热传导矩阵/固定温度边界/热通量/热流密度/对流换热/体积热源/平面热传导/三维热传导_哔哩哔哩_bilibili
目录
导读:上一篇文章从传热学基础到弱形式推导:拆解热传导问题Matlab有限元离散核心讲述了我的仿真秀官网原创首发的视频课程《热传导问题Matlab有限元编程》第2~4讲的主要内容,带读者熟悉传热学的基本概念、控制方程及弱形式推导过程。本文介绍《热传导问题Matlab有限元编程》视频教程的第5~7讲,主要带大家了解三维传热问题控制方程(三维泊松方程)、单元类型选择(八节点六面体)、形函数构造(自然坐标下的双线性形式)、等参变换的实质(坐标-函数用同一形函数映射)、刚度矩阵和热载荷的积分计算(高斯积分在三维的应用)、边界条件处理(三类边界在三维表面的积分),以及组装求解的通用流程等内容。
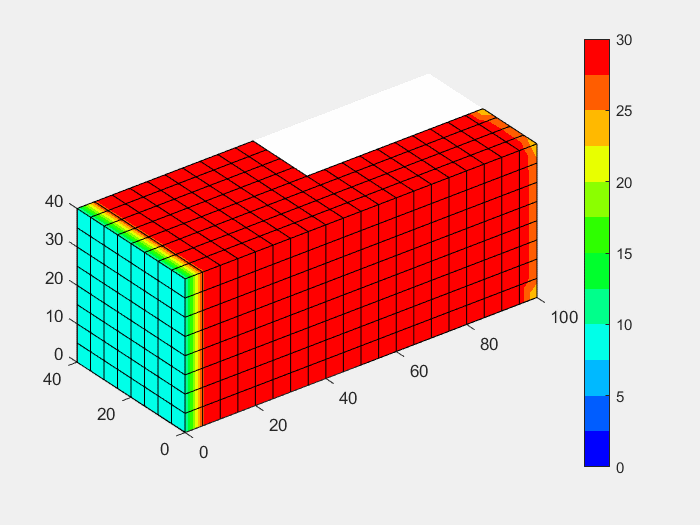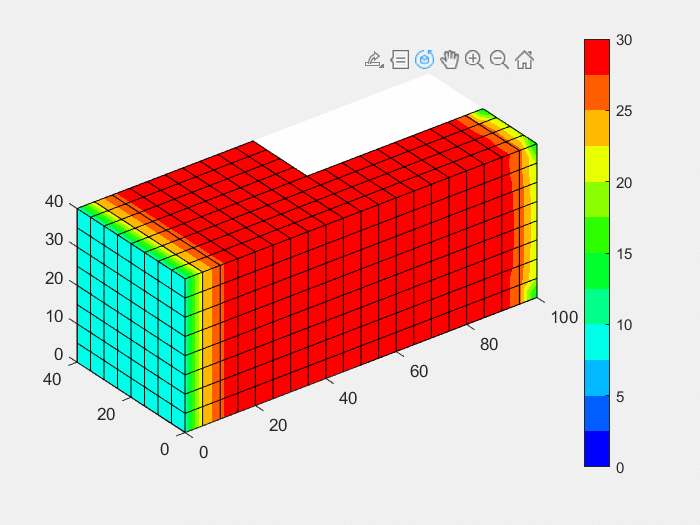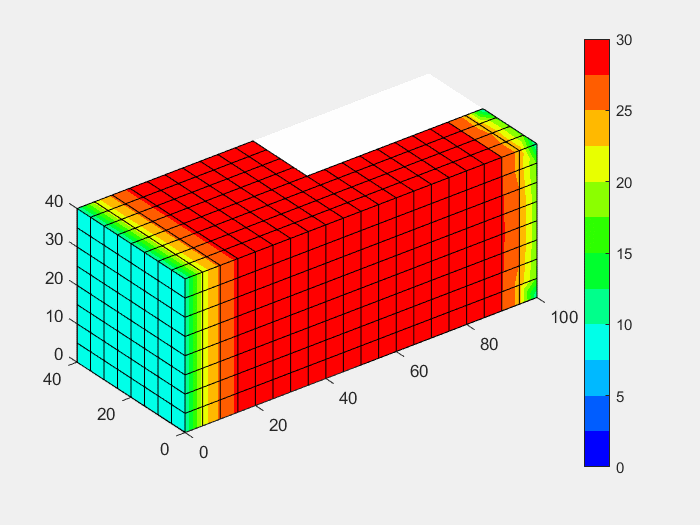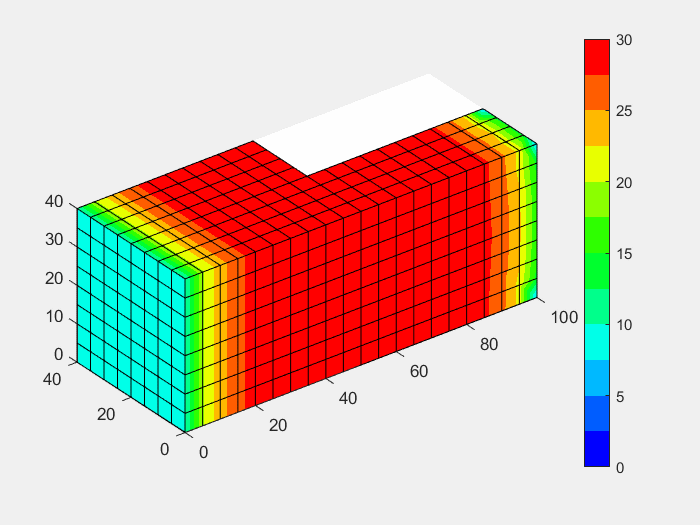
由于内容较多,因此分为上下两篇,上篇重点介绍相关的有限元理论及公式的推导,下篇则侧重编程实现方法。因为二维传热问题是三维传热问题的简化和抽象,因此三维传热问题相比二维传热问题理解起来更直观更简单,所以我们先从理解起来比较简单的三维传热问题入手有限元编程,采用的单元也是常用的六面体单元,求解精度对标ANSYS中的solid70单元,误差小于1%。
我们还会介绍热传导方程的弱形式推导以及带入形函数进行有限元离散的过程,这个过程会涉及伽辽金加权残值方法、格林公式(分部积分)、泛函驻值等弱形式推导过程中用到的理论知识。文章最后阐述了我对一个问题的理解:为什么有限元离散需要基于控制方程的弱形式?
【案例源码获取入口】
六面体传热单元(体积热源)有限元MATLAB程序【理论文本+代码】|热传导有限元|对流换热边界条件|有限元传热分析
六面体传热单元(热对流边界条件)有限元MATLAB程序【理论文本+代码】|热传导有限元|对流换热边界条件|有限元传热分析
六面体传热单元(固定温度边界条件)有限元MATLAB程序【理论文本+代码】|热传导有限元|狄利克雷边界|有限元传热分析
六面体传热单元(热通量边界条件)有限元MATLAB程序【理论文本+代码】|热传导有限元|纽曼边界条件|有限元传热分析
一、传热学基本概念
·热传导控制方程
如果你有结构力学有限元编程的基础,可以通过类比的方法去理解传热有限元编程:与弹性力学问题的求解相同, 热传导问题的求解也是通过插值函数进行离散之后, 从泛函驻值条件建立起有限元求解方程。不同之处在于场变量,在弹性力学问题中场变量是位移, 是向量场, 而热传导问题中场变量是温度, 是标量场。因此, 热传导问题要比力学问题相对简单些。
我猜我们大多数人是比较熟悉结构力学有限元编程的一些概念,其实许多热传导物理量可以与弹性力学问题中的物理量进行类比, 比如位移与温度, 比热容与密度 (对于瞬态问题表示场变量的惯性效应, 稳态问题不起作用), 节点热流量和节点力,对流换热表面热通量与表面分布力,位移边界条件与固定温度边界条件,热源与体积力。注意区分热通量与热流量的概念,热通量(heat flux)表示单位时间单位面积内通过的能量,单位 W/m^2,热通量也叫热流密度;热流量(heat flow)可以简单理解为热量,表示一段时间内热量的变化,重点是量, 不存在单位面积体积的概念, 单位是 W , 可以简单理解为热通量在边界上的面积积分就是热流量,热流量也称热流率。
传热学中,对于一个三维实体,t 时刻的瞬态温度
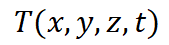
的计算公式如下,
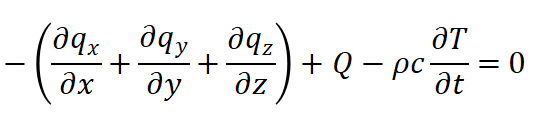
(1)
其中
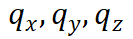
为热通量分量, 将
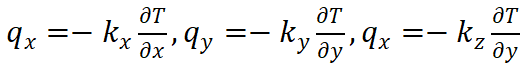
代入式(1)可得:
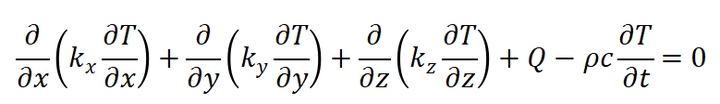
(2)
其中: x,y,z 为热传导主方向;
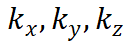
分别为x,y,z方向的热传导系数;
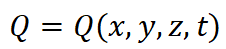
是单位体积发热率;
rho是材料密度; C是比热。对于稳态传热问题,公式 1 中的时间偏导项可忽略不计。初始条件如下;
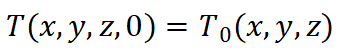
(3)
边界条件暂不考虑热辐射边界条件,主要包含以下三种:
(1) 温度边界条件:
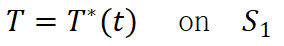
(4)
(2) 热通量边界条件:
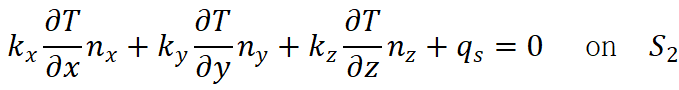
(3) 对流换热边界条件:
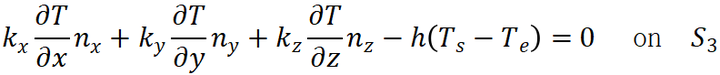
(5)
其中:
T*为特定嗢度;q为热通量;h为对流换热系数;
nx,ny,nz分别为边界朝外的正方向;
Ts为表面温度;
Te为环境温度。
二、有限元方程的建立
三维六面体实体热单元,可以用于模拟三维热分析。该单元由8个节点构成,节点有1个自由度:温度。单元几何形式如下图所示:
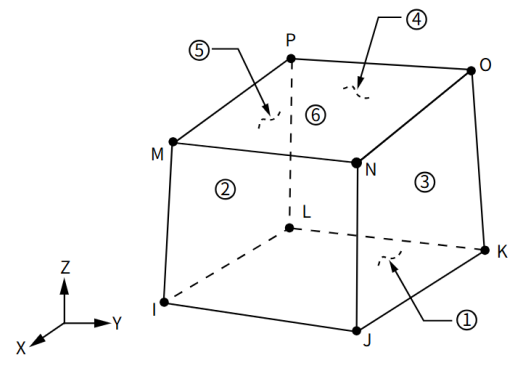
图2-1 三维六面体实体单元示意图
1、单元形函数
三维8节点六面体实体单元中任意一点的坐标如式(1)所示。
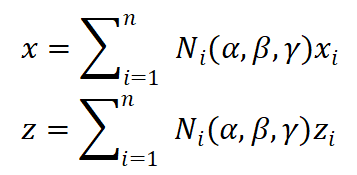
(6)
其中:(x,y,z)为单元内任意一点的空间位置坐标,
为自然坐标,
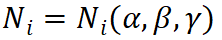
为形函数,
i=8为节点序号,形函数Ni的表达式如下:
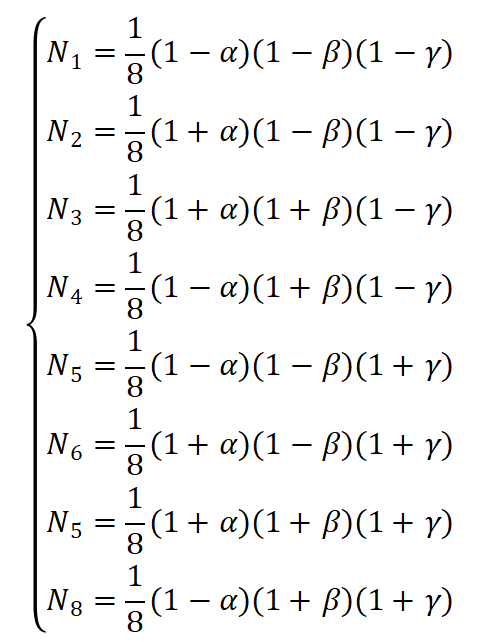
(7)
也可以简单表示为:
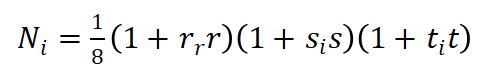
(8)
三维六面体实体单元不考虑发热率和对流换热问题,发热率和对流换热将由专门的单元实现,因此式(4-7)和(4-8)可忽略。
单元中的温度可以通过形函数插值得到:
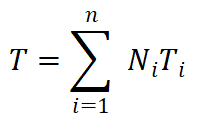
(9)
或以矩阵形式表示为:\
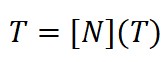
(10)
其中:
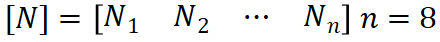
为形函数矩阵;
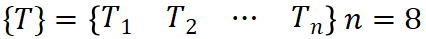
为节点温度矩阵。
对式(10)进行偏分得到:
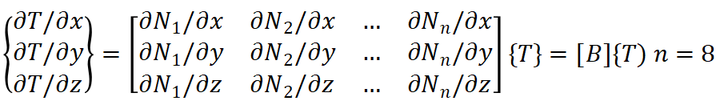
(11)
其中[B] 为温度梯度插值矩阵
2、弱形式的推导
采用 Galerkin 方法,权函数等于插值函数。将热控制方程与权函数相乘并在计算域内积分,式(1)可表示为:
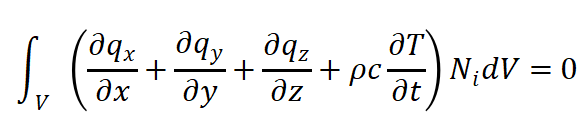
(12)
对前 3 项应用发散定理可得:
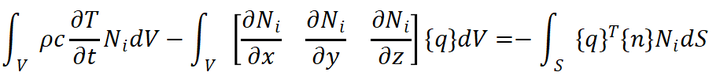
(13)
其中:
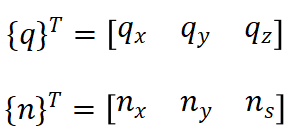
将边界条件代入式(13)可得:
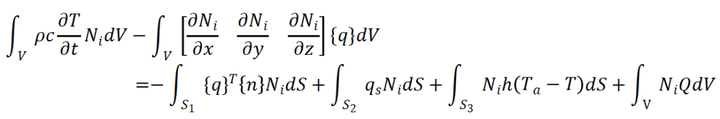
3、刚度矩阵和热流向量
在上一节的控制方程弱形式的基础上,带入式(6~8)关于形函数的表达式以及式(9~10)所示的温度场的离散表达式,可以直接将
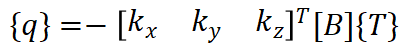
代入弱形式表达式可得:
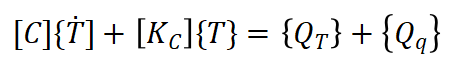
(14)
其中:
C\]为比热矩阵: 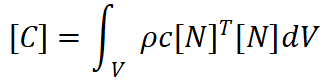 (15) \[Kc\] 为热导率矩阵: 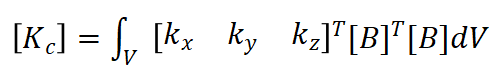 (16) \[H\]为修正矩阵 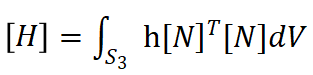 (17) Qt为温度边界条件产生的热流量: 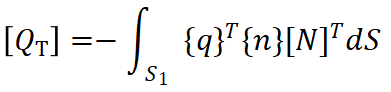 (18) Qq为热通量边界条件产生的热流量: 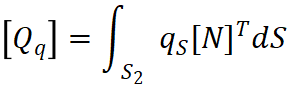 (19) Qc为对流边界条件产生的热流量: 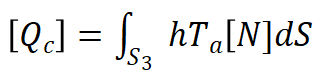 (20) Qq为体积热源产生的热流量: 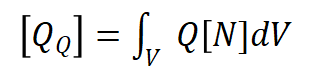 (21) #### 4、等参单元与高斯积分 在对上述公式采用高斯数值积分方法进行完全积分前, 先将空间坐标系转换为自然坐标系 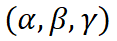 ,空间坐标系与自然坐标系之间的转换矩阵即为 Jacobian 矩阵,可表示为: 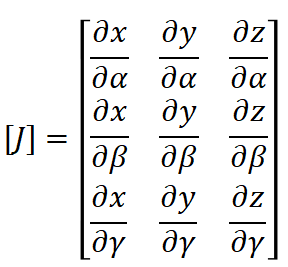 (22) 将式(1)代入式(5-2)可得: 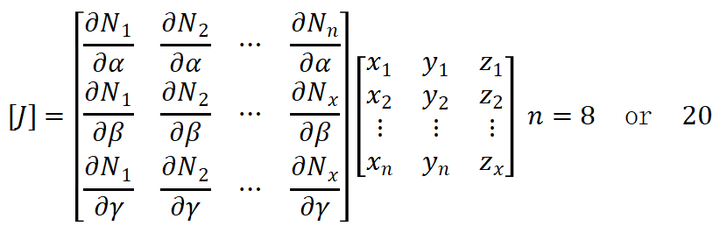 添加图片注释,不超过 140 字(可选) (23) 假设 Jacobian 矩阵是可逆的, 则可以得到: 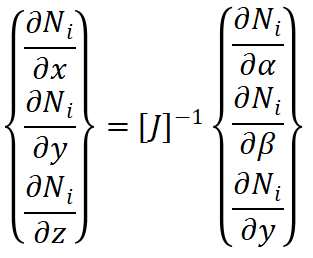 (24) 经过 Jacobian 矩阵转换,比热矩阵式(15)可表示为: 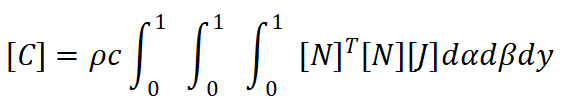 (25) 热导率矩阵式(16)可表示为: 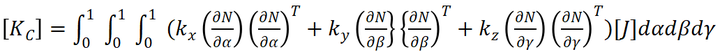 (26) 以上就是关于六面体单元的有限元方程的推导。由于篇幅问题,其他内容请查看后续文字。更多内容可参考我的《热传导问题Matlab有限元编程》视频课程! ### 三、为什么要学习这门课程 回到我们的课程,热传导分析是工业设计的重要支柱,从电子芯片的散热优化到航天器的热防护设计,从金属成型的热处理到建筑节能的温度场模拟,这些看似迥异的工程问题背后都遵循着相同的传热学规律。 本课程将带您突破有限元在结构力学领域的应用范围,在Matlab平台上构建全新的传热问题的有限元求解体系,并通过解决热固耦合问题,将有限元在传热领域和结构力学领域的应用融会贯通,最后你会惊喜地发现:无论是热传导方程还是结构力学方程,其有限元求解的本质,竟都扎根于偏微分方程的数值离散之道。以下是我认为学习这门课程价值所在: 1、全链路实战:从理论到工业级代码落地。课程内容覆盖传热学基础、有限元弱形式推导、稳态 / 瞬态求解、热固耦合等核心理论,配套 2D/3D 单元(tri3/quad4/tet4/hex8)代码实现,对标 ANSYS 精度(误差 \<1%),真正做到 "理论懂原理,编程能上手"。 2、破解商业软件 "黑箱":掌握结果背后的逻辑。深入讲解三类边界条件(固定温度、热流密度、热对流)、体积热源施加的底层算法,让你理解仿真结果的误差来源、合理性判断依据,不再盲目依赖软件输出。针对非常规问题(如特殊热源、复杂耦合场景),教你开发专用工具,满足科研中的参数化研究、优化设计等定制需求,为论文或项目提供独家数值支持。 3、热固耦合全掌握:从温度场到应力场一站式求解。涵盖间接耦合(先求温度场再算热应力)和直接耦合(同步求解温度、位移、应变场),完整复现工业级热 - 结构耦合仿真流程,适应机械、航空航天等多领域需求。